基于自然单元法的2.5维直流电阻率数值模拟

王佳新, 崔益安, 谢 静, 罗议建, 柳建新

(1.中南大学 地球科学与信息物理学院，长沙 410083；2.中南大学 有色资源与地质灾害探查湖南省重点实验室，长沙 410083；3.中南大学 教育部有色金属成矿预测重点实验室，长沙 410083)

0 引言

直流电阻率法数值模拟研究中，常用的数值算法包括有限单元法[1-3]及有限差分法[4]等网格法，但其在处理复杂、不规则地电模型过程中严格受网格约束，需要开展大量繁琐的前期工作，影响计算效率、效果[5]。针对复杂模型适应性问题，麻昌英等[6]采用全局弱式无单元法对复杂地电条件下的直流电阻率模型开展数值模拟。该方法虽摆脱了网格的限制，但形函数构造复杂、计算量大、边界条件施加困难。

自然单元法是一种新型的无网格数值方法，最早由Braun等提出[7]。该方法基于Voronoi图[8]和Delaunay三角剖分[9]，采用Sibson[10]或non-Sibson[11]自然邻点插值方法构造试函数，求解偏微分方程。自然单元法不仅具有无网格法和网格法的优点，还克服了它们的缺陷。与无网格法相比，自然单元法的计算量小，计算效率高；与网格法相比，自然单元法不受网格限制，只需要自然节点信息，这对复杂模型的剖分具有重要意义[5]。目前自然单元法主要应用于材料力学领域[12-14]，而很少见其在勘探地球物理领域中的应用报道[5, 15-16]。

这里首次成功将自然单元法应用于直流电阻率法数值模拟研究中，探究该算法在该领域的可行性及模拟效果。首先从2.5维点源场边值问题出发，推导其满足的变分及积分形式基本方程。随后推导二维情况下的自然单元法形函数及其导数的基本方程。最后通过一系列数值算例验证该算法的有效性，证明其在直流电阻率模型中的适用性。

1 2.5维点源场基本方程

对于点源位于地表的二维地电模型，其满足的2.5维稳定直流场边值问题可表示为[17]：

▽·(σ▽U)-k2σU=-I0δ(A)

(1)

(2)

(3)

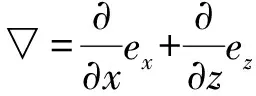
笔者欲采用自然单元法求解该边值问题，需先将其变换为变分问题。可表达为式(4)[17]。

(4)

在任意积分网格中，式(4)中的各项积分可表示为[17]：

(5)

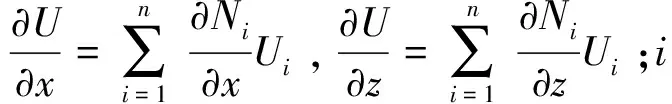
(6)

源积分项及边界积分项详见文献[17]。最后将各积分按节点编号累加至总刚度矩阵中，由变分为0可得到线性方程组：

KU=P

(7)

其中:K为总刚度矩阵;U为待求波数域电位向量；P为源向量。求解公式(7)即可得到各节点波数域电位值，而后再通过傅里叶反变换求解得到二维空间中任意一点的电位值：

(8)

其中采用的波数及其权值系数见表1[17]。

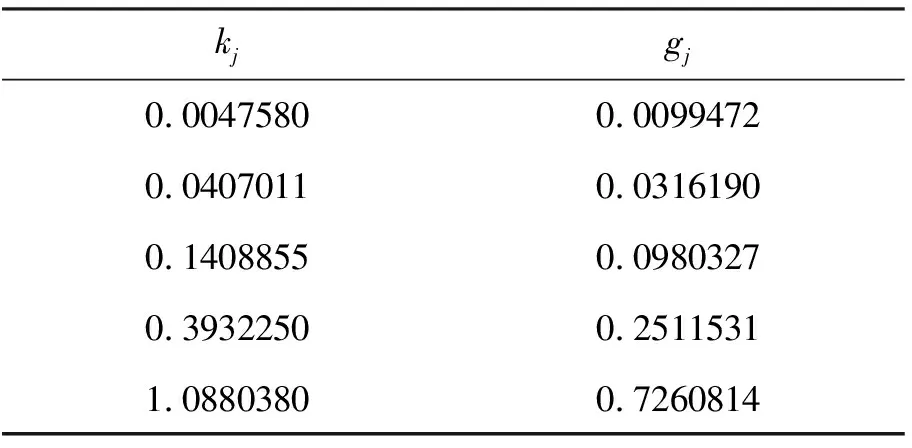
表1 波数k及其权值系数g

2 自然单元法

数值模拟算法的本质区别是构造形函数的方式不同，其影响数值模拟过程的计算效率、精度、复杂度等。自然单元法作为一种无网格法，仅需节点信息即可构造插值形函数，且整个过程可利用复合函数链式求导法则简化为系列加减乘除计算，能有效保证计算效率。

Voronoi结构和Delaunay三角剖分是由一组离散点定义的最基本的几何结构。如图1所示[5]，假设在平面内给定7个离散节点，作任意两节点的垂直平分线(图1(a))，各半平面的交集构成多个凸多边形区域，即为一阶Voronoi单胞结构(图1(b))；进而将所有具有共同边界的Voronoi单胞对应的节点连接成三角形网络以构成Delaunay三角剖分(图1(c))。

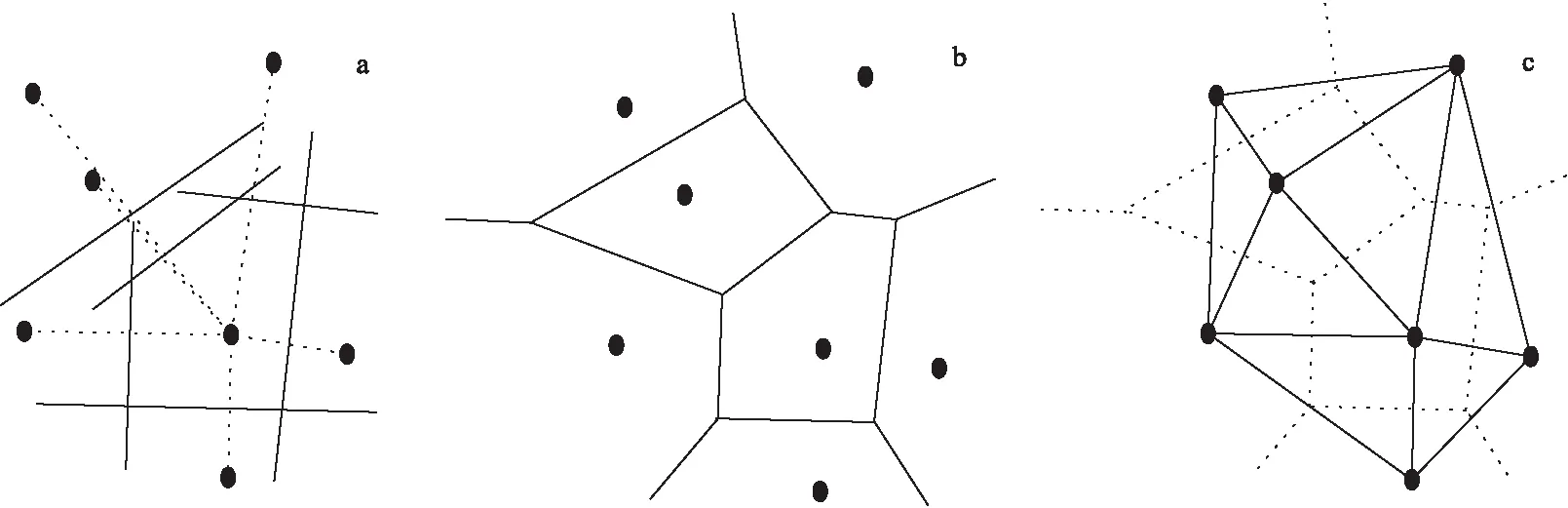
图1 Voronoi图和Delaunay三角化Fig.1 Voronoi,Delaunay triangularization(a)7节点系统的Voronoi剖分；(b)7节点系统的Voronoi单元；(c)7节点系统的Delaunay三角剖分

基于Voronoi结构和Delaunay三角剖分，可以搜索各积分点的自然邻点并构造插值函数。笔者选用简便易行的non-Sibson (也称为Laplace)自然邻点插值格式[5, 18]。自然单元法形函数构造过程如图2所示。插值形函数可写作式(9)。

(9)

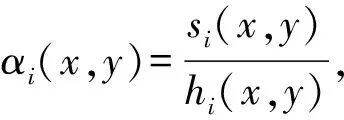
以图2(b)中的积分点X为例，其自然邻点为节点1、2、3、4。节点12、23、34、41分别为三角形1-2-X、2-3-X、3-4-X、4-1-X的外接圆圆心。对于任意三角形ABC，令其顶点坐标分别为(x1,y1)、(x2,y2)、(x3,y3)，其中C(x3,y3)与积分点X重合，则该三角形的外接圆圆心坐标可表示为：

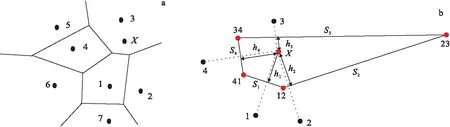
图2 Non-sibson插值法Fig.2 Non-sibson interpolation(a)假设点X为7节点系统的某积分点；(b)插值点X的自然邻点及non-Sibson插值参数

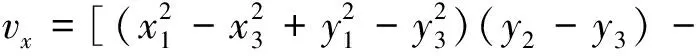
(10)

(11)

(12)

(13)

(14)

(15)

其中：

D=2[(x1-x3)(y2-y3)-

(x2-x3)(y1-y3)]

(16)

α=(x2+x1)(x2-x1)+

(y2+y1)(y2-y1)

(17)

D,x=2(y1-y2)

(18)

D,y=2(x2-x1)

(19)

其中:vx和vy为外接圆圆心坐标；vx，x、vx，y、vy，x、vy，y为圆心坐标对坐标轴的偏导；α和D为中间变量；Dx和Dy表示D对坐标轴的偏导。

设任意Voronoi边的两个端点坐标为V1(vx1,vy1)和V2(vx2,vy2)，则si(x,y)可表达为：

(20)

进一步地，插值形函数的偏导可表示为：

(21)

(22)

其中：

(23)

(24)

si,x(x,y)=[(vx1-vx2)(vx1,x-vx2,x)+

(vy1-vy2)(vy1,x-vy2,x)]/

(25)

si,y(x,y)=[(vx1-vx2)(vx1,y-vx2,y)+

(vy1-vy2)(vy1,y-vy2,y)]/

(26)

(27)

(28)

(29)

将公式(9)～公式(29)带入公式(5)、公式(6)，即可求解方程组(7)。其中，边界条件的加载可类比点源二维电场的有限单元法处理过程[17]，即将边界处相邻的两个自然节点看作网格的无穷远边界。最后由公式(8)计算得到二维模型空间的电位分布，进而计算地下视电阻率分布情况。

3 数值算例

为验证自然单元法在2.5维稳定直流场数值模拟中的有效性，笔者对一系列直流电阻率地电模型进行算例分析。

3.1 水平层状模型

采用水平层状模型进行解析解验证。其中上层电阻率为100 Ω·m，厚度为10 m，下层电阻率为10 Ω·m。采用固定点源的二极装置进行测量，供电电极A位于(0, 0)处，测量电极M从(0, 1)逐渐移动至(0, 80)。161×161个自然节点均匀布设在二维地电模型中。视电阻率曲线如图3所示。

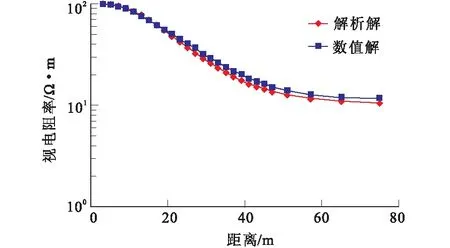
图3 水平两层介质视电阻率曲线Fig.3 Apparent resistivity curves of a two-layered model

从数值结果可以看出：对于测区[0, 20]，数值计算结果与解析解吻合很好，而随着测点M逐渐靠近边界，自然单元法的计算精度呈现一定的误差 (相对误差在1%～10%之间)，但与常规有限单元法的计算结果[1]相比满足精度需求。

3.2 均匀半空间中赋存块状异常体

均匀半空间中赋存3个块状电阻率异常体的验证模型(图4)。Xu等[19]采用该模型验证了边界元法，肖晓等[1]采用该模型验证了有限元-无限元耦合法。笔者采用自然单元法计算该模型，并与参考文献[1]及参考文献[19]的计算结果相比较，以验证自然单元法的有效性。

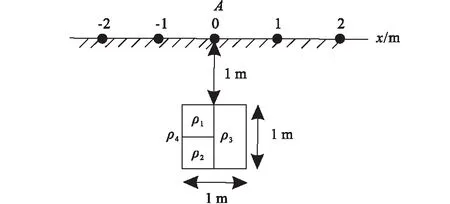
图4 均匀半空间中赋存3个块状异常体Fig.4 Three blocks buried in homogeneous half-space

如图4所示，3个异常体的电阻率分别为ρ1=0.1 Ω·m、ρ2=10 Ω·m、ρ3=50 Ω·m，均匀半空间电阻率为ρ4=1 Ω·m。整个异常体的边长为1 m，顶部埋深为1 m。模型空间由321×321个自然节点均匀填充。采用二极AM装置进行测量，点源A位于(0, 0)处且固定不动。测定M从-10 m移动到10 m处，电极间距为2 m。

图5为边界元法[19]、有限元法[1,19]以及自然单元法的计算结果。可见自然单元法的计算精度与边界元法、有限单元法等相当，进一步验证了算法的有效性和计算精度。

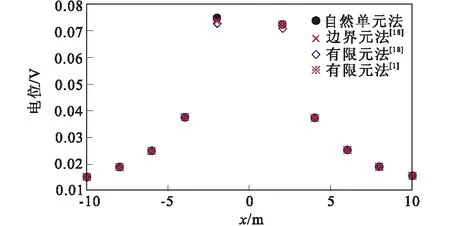
图5 不同方法计算的电位对比Fig.5 A comparison of potential calculated with different methods

3.3 均匀半空间中赋存三棱柱体

采用均匀半空间中赋存三棱柱的地电模型，验证自然单元法对复杂几何体的有效剖分。模型如图6所示，模型空间共布设61×31个自然节点，其中不规则目标体由自然节点灵活填充。三棱柱体电阻率为10 Ω·m，背景电阻率为100 Ω·m。三棱柱体的三角形面为高度等于10 m的等腰三角形，顶部埋深为10 m。采用对称四极装置进行测量。视电阻率断面如图7所示。数值结果表明，自然单元法能有效剖分复杂地电模型，且能够较好地反映地下异常体的分布特征。

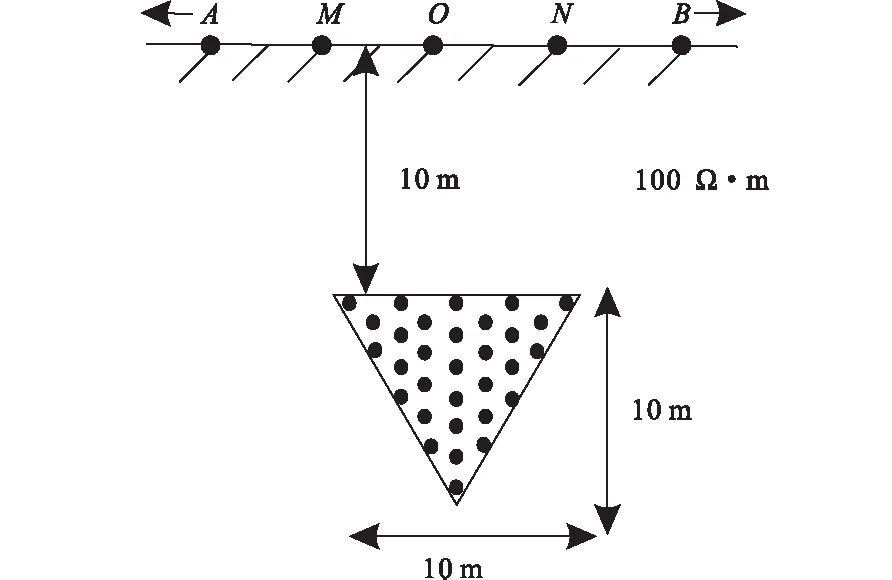
图6 均匀半空间赋存三棱柱模型示意图Fig.6 Infinite horizontal tri-prism buried in homogeneous half-space

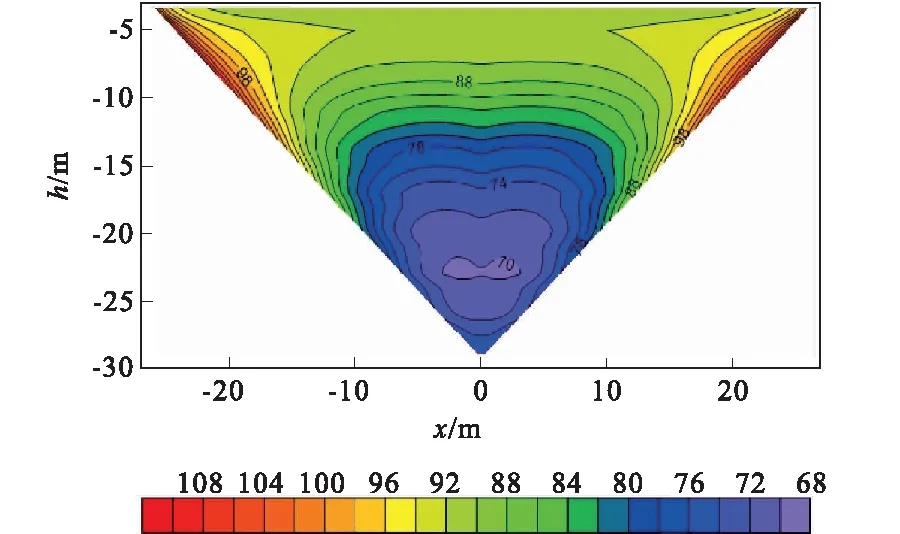
图7 均匀半空间中赋存三棱柱体视电阻率断面图Fig.7 Section of apparent resistivity for a triangular prism buried in homogeneous half-space

3.4 地质体模型

图8所示地电模型中赋存两个电阻率异常地质体。模型尺度为80 m×40 m，由81×41个自然节点均匀填充。背景电阻率为100 Ω·m；高阻体尺度为5 m×5 m，电阻率为1 000 Ω·m；低阻体尺度为5 m×5 m，电阻率为10 Ω·m。两异常体相距10 m，且顶部埋深均为1 m。采用对称四极装置进行测量。图9为视电阻率断面，可见自然单元法能较好反映电阻率异常体的分布特征。

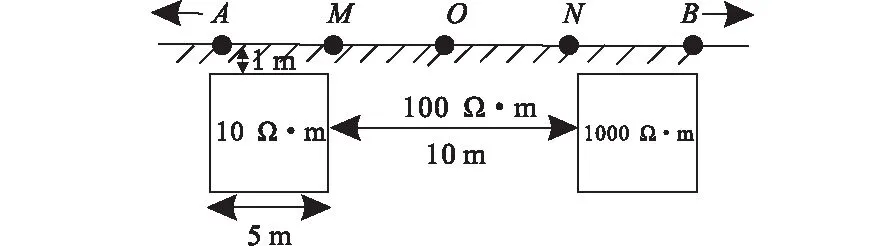
图8 均匀半空间中赋存2个块状异常体Fig.8 Two blocks buried in homogeneous half-space

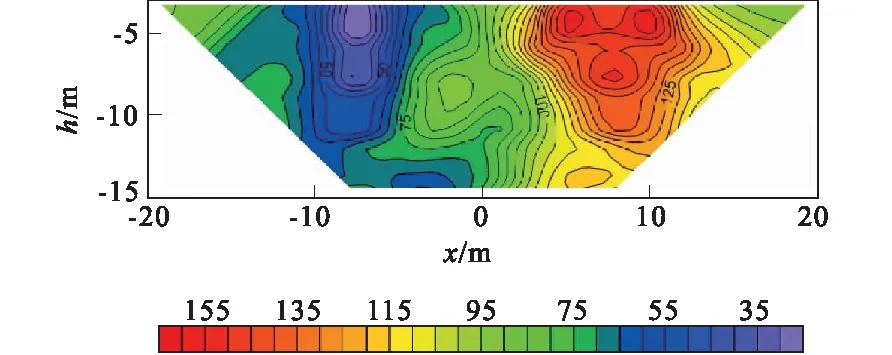
图9 均匀半空间中赋存2个块状异常体视电阻率断面图Fig.9 Section of apparent resistivity for two blocks buried in homogeneous half-space

4 结论

首次将自然单元法引入直流电阻率模型数值模拟研究中，给出了详细的公式推导，并通过4个地电模型验证该算法的可行性，得到以下结论：

1) 自然单元法在直流电阻率法数值模拟领域是有效的，且计算精度满足需求。

2) 自然单元法在构造形函数时只需要节点信息，且基于复合函数的链式求导法则使得计算过程简单明了易编程实现。

3) 自然节点布设灵活，能较好地填充复杂异常体，适用于复杂模型数值模拟研究。