基于Monte carlo法的Rayleigh波浅层横波速度结构反演方法研究

胡昌荣, 黄金强,2, 刘 宏,2, 窦勇硕, 何云川

(1.贵州大学 喀斯特地质资源与环境教育部重点实验室，贵阳 550025；2.贵州大学 资源与环境工程学院，贵阳 550025)

0 引言

近地表横波速度值，是公路桥隧建筑等抗震设计、土壤级别划分及地层软硬程度判定的关键参数之一，在浅层岩土工程勘察、设计与施工中应用十分广泛[1-3]。目前，横波速度反演主要有：基于多波多分量数据的弹性波层析建模方法、基于频散特征的面波方法以及近几年提出的面波全波形反演方法。其中面波全波形反演具有反演质量高、不受硬表层及低速半空间影响等优势，但却存在计算成本高、反演效果受限于数据品质及方法并未完全实用化等缺点；多波多分量弹性波法因震相拾取困难，大多应用于孔间地层速度反演，对施工要求较高；而基于频散特征的面波法不仅采集方式简单易行，操作方便，还具有数据处理方法较为稳定可靠的优势。然而，基于非线性全局优化反演算法的面波反演策略，仍然存在诸如计算效率低、收敛迭代慢和内存占用高等问题，为此，进一步发展一种快速且稳定的反演方法就显得极为重要。

Rayleigh波勘探技术具有非损伤性、低成本及勘探高效性等优点，备受浅地表地球物理及工程地质学界重视，是当前最具潜力的勘探技术之一[4]。面波谱分析方法(SASW)最早由Nazarian等[5]提出，但该方法在实际浅地表工程应用中存在提取频散曲线的抗干扰能力差等缺陷。随后，美国堪萨斯大学Park等[6]进一步提出面波多道分析技术(MASW)，该方法有效地弥补了SASW方法的不足。由于基于主动源的面波多道分析技术在提取频散曲时具有精度低等问题，Park等[7]将主动源及被动源优势相联合，进一步发展和系统研究了MASW技术。在MASW技术中，高频Rayleigh波勘探技术大致可分为4个具体步骤：①面波数据采集；②数据预处理与频散曲线提取；③初始模型估计并进行频散曲线的正演计算；④频散曲线反演横波速度。由于Rayleigh波在非均匀介质中传播具有频散特征，通过Xia等[8]研究结果表明，Rayleigh波频散方程对横波速度及层厚最为敏感，因此利用Rayleigh波频散特征来反演浅地表横波速度与层厚具有明显优势。但是在一些特殊模型中，频散方程对模型参数的敏感性较低，反演还存在一定的技术问题：①在低速半空间中Rayleigh波频散方程在某些频率求解下存在复数根，导致在某些频率下无法正常获取Rayleigh波相速度，因此，Pan等[9]提出了用复数根实部作为Rayleigh相速度，有效解决了该问题，但低速半空间的反演问题是一个复杂问题，局部线性化方法反演低速半空间横波速度的适用性将大大降低；②若表层的横波速度高于下伏地层时，高频处的Rayleigh相速度将趋近于除半空间以外其他层的最小横波速度值，而不是趋近表层横波速度相关的某个值，Pan等[10]提出采用“替代”的方法来解决Rayleigh波波长不足以穿透最低横波速度的层厚时引起地计算错误，但是基于Monte Carlo反演策略在反演高速表层模型时结果却并不令人满意；③地下介质表现为横向不均匀时，在求解水平层状介质中Rayleigh波的本征值问题之上开展的Monte carlo局部线性化反演算法，在反演横向不均匀介质时，反演效果不佳。

MASW技术将采集得到的t-x域多道Rayleigh波信号通过一定方法变换到f-v域，从而提取Rayleigh波频散能量(如：f-k变换法[11]、高线性拉东变换[12]、τ-p变换法[13]、相移法[14]等)。Rayleigh波频散曲线是浅地表地下特征的综合反映，在利用Rayleigh波频散特性反演横波速度中，分别为非线性全局优化算法及局部线性化反演算法两大类。基于局部线性化反演算法在求解非线性问题时，每一次迭代过程都将朝向目标函数取极小值，为快速求解全局极小值，前人们提出了各种最优化算法，Xia[8]采用改进的阻尼最小二乘反演策略提高了Rayleigh波频散曲线反演的计算效率，但局部线性化反演算法强烈依赖初始模型，若初始模型选取不当易陷入局部极小值。因此，学者们进一步发展了不依赖于初始模型的非线性全局优化反演算法，提出了彻底搜索法、Monte carlo反演算法、改进的Monte carlo反演算法等。但是在非线性全局优化反演算法中，彻底搜索法对模型参数所组合到的所有模型进行空间搜索，存在计算机的海量计算[15]。而基于概率论观点的Monte carlo反演算法[16]，以随机方式进行模型的空间搜索，有效避免了计算机的海量计算，在非线性全局优化反演算法中得到了广泛应用[17-18]，但在Monte carlo反演算法中，若没有足够的先验信息引导随机搜索，将存在计算机的“盲目”及完全随机搜索，极大增加了计算量。为此，随着计算机技术的迅速发展，一些改进的Monte carlo反演算法也得到了广泛地应用(如遗传算法、退火算法、BP神经网络等)。但此类方法仍然存在计算效率低、迭代慢、计算机内存占用高等问题。如：石耀霖等[19]用非线性遗传算法反演地球内部构造时，该算法存在不能保证找到最优解的缺点，同时易出现“早熟收敛”或收敛速度极慢等问题。基于“启发”式随机搜索的模拟退火算法对地层横波各向异性进行反演时，存在计算速度慢等问题[20]。基于BP神经网络的Rayleigh波智能优化反演横波速度时，存在网络训练耗时较长以及针对不同地震模型需要重新网络训练等繁琐问题，其次若训练样本过大也将影响收敛速度等缺点[21]。因此，在求解水平层状介质中Rayleigh波的本征值问题之上，采用Monte carlo局部线性化反演算法，该算法不仅具有计算速度快、计算机内存占用小等优势，还有效避免了Monte carlo反演算法中的“盲目”及完全随机搜索。

综上所述，笔者在MASW技术中，借鉴Press的思想，在求解水平层状介质中Rayleigh波的本征值问题之上，采用Monte carlo局部线性化反演算法获取浅地表横波速度值[22]，并进一步在典型数值算例中，对比分析了基于Monte Carlo反演策略与经典阻尼最小二乘反演策略，验证了基于Monte Carlo反演策略在求取浅层横波速度方面的优势。

1 方法原理

1.1 Monte carlo反演算法

改进的Monte carlo反演算法在获取浅地表横波速度中存在固有的计算效率低、迭代慢、计算机内存占用高等问题(如遗传算法、BP人工神经网络、退火算法等)。因此借鉴Press的思想，在求解水平层状介质中Rayleigh波的本征值问题之上，采用Monte carlo局部线性化反演算法获取浅地表横波速度值可避免此类问题。在Monte carlo反演算法中为避免“盲目”及完全随机搜索，采用空间约束方法，对解的范围进行空间约束，这极大提高Monte carlo反演算法的计算效率，具体推导过程如下：

在求解水平层状介质中Rayleigh波的本征值问题上，可将水平层状介质模型中的每层横波速度值、层厚值、密度值及纵波速度值分别定义为Vs、h、ρ、Vp的集合。

Vs={Vs1,Vs2,…,Vsn}

h={h1,h2,…,hn}

ρ={ρ1,ρ2,…,ρn}

Vp={Vp1,Vp2,…,Vpn}

(1)

通过改进的Haskell-Thomson传递矩阵算法正演频散曲线[22](详见附录A)可计算Rayleigh波理论频散曲线。

(2)

其中：c为Rayleigh波相速度;k为波数;n为层数;i为给定波数所对应的Rayleigh波相速度的点数。

因此在Haskell-Thomson传递矩阵正演算法的基础上，已知实测频散曲线反推地质模型。首先，根据实测频散曲线的形态特征逻辑推断反演的初始模型Vs、h、Vp、ρ(图1)。其次，定义当前初始模型Vs、h的空间范围：

(3)

图1 实测频散曲线的参数估计Fig.1 Parameter estimation of measured dispersion curve(a)实测频散曲线;(b)模型参数

Δj=Ω(-γ·Vs,γ·Vs)

Δl=Ω(-δ·h,δ·h)

式中：Δj、Δl分别表示横波速度及层厚度模型的采样空间，由于在采样空间中能随机抽取到无数个值，因此，j表示在采样空间中某一层横波速度能取到的值的个数，l表示在采样空间中与横波速度所对应的地层中层厚度能取到的值的个数，γ、δ为常数，将对横波速度及层厚度采样空间进行约束，即：对横波速度及层厚度的解的空间范围进行约束。

随后，在一定空间范围内随机生成每一次正演的样本模型:

Vsj=Vs+Δj

hl=h+Δl

(4)

为获取相应地层中的Vp值，根据Everett[23]提出的纵横波速度比与泊松比的关系进行纵波速度值推算：

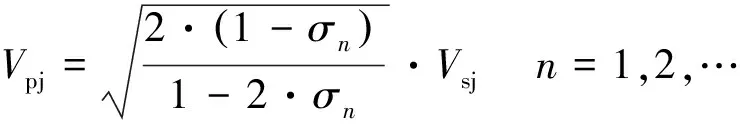
(5)

通过密度与纵波速度经验公式对相应地层中的密度值进行计算[24]：

(6)

最后，将随机生成的每一次迭代样本模型{Vsj,Vpj,ρj,hl}，利用改进的Haskell-Thomson传递矩阵算法进行正演，以此得到每一个模型的频散曲线。

1.2 阻尼最小二乘反演算法

Rayleigh波频散方程与模型参数Vs、Vp、ρ、h有关，但频散方程对横波速度Vs的敏感性极高，因此阻尼最小二乘为减少待反演的模型参数，在反演时将其余参数Vp、ρ、h作为已知变量，并在反演过程中保持不变，只将Vs作为反演过程中的独立变

量，这极大提高了反演的计算效率。为此进一步将频散方程式(2)简述为式(7)[8]。

(7)

由于大多数地球物理问题并非线性问题，为使非线性问题线性化，根据泰勒级数定理，将式(7)中ci在初始值ci,0处展开并取一阶近似可得：

(8)

进一步采用矩阵方程形式将式(8)表述为式(9)。

(9)

表述的矩阵方程式(9)可进一步简述为：

Δc=AΔx

(10)

式中：Δc=ci-ci,0,i=1、2、…、M，表示M维长度的Rayleigh波相速度残差向量;A表示一阶偏导数组成的M×n维雅格比矩阵;Δx=Vsq-Vsq,0,q=1、2、…、n，表示n维长度的横波速度残差向量。

针对线性最小二乘反演问题，可将目标函数表述为若干个函数的平方和形式:

(11)

式中：ciobs表示实测Rayleigh波相速度值，cical表示理论Rayleigh波相速度值。

为使最小二乘的目标函数最小化，采用L-M方法进行改进[8,15,25]，根据L-M方法的原理，将式(10)带入式(11)，可将目标函数表述为矩阵的形式：

φ(Vs)=‖AΔx-Δc‖2W‖AΔx-

(12)

式中：‖‖2表示l2范数;W表示权重矩阵;λ为阻尼因子。

进一步将目标函数简化并整理得：

(ATA+λI)Δx=ATΔc

(13)

式中：AT表示雅格比矩阵A的转置;I为单位矩阵。

通过移项并整理得到方程(12)的解：

Δx=(ATA+λI)-1ATΔc

(14)

式(14)中，通过引入阻尼因子λ，可避免“病态”系数矩阵导致的求解过程不稳定，同时也控制着Δx的大小，由于λ的每一次变化，将引发计算的繁琐，因此采用奇异值分解方法计算广义逆矩阵，将雅格比矩阵A奇异值分解表述为：

A=UΛVT

(15)

将式(15)带入式(13)可得式(16)。

(16)

即有：

(17)

进一步整理得：

(18)

从式(18)中可见，在对角矩阵中，λ的每一次变化，不会引发繁琐的计算。

(19)

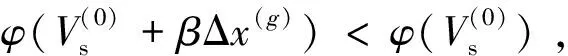
(20)

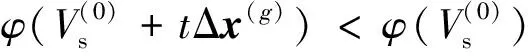
1.3 Monte carlo 检验准则

采用均方根误差定义每一条频散曲线与实测频散曲线的误差，将均方根误差[26]作为样本模型的检验标准，若误差达到最小时，则接收该样本模型是最优模型，反之，则排斥该样本模型。具体反演算法流程如图2所示。

(21)

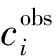
2 模型测试/数值模拟

2.1 三层模型实验

笔者首先利用三层层状模型，通过Rayleigh波有限差分正演模拟合成单炮面波正演记录，随后通过相移法[14]提取频散曲线(详见附录B)，最后通过设置两组不同的初始模型，分别对比了基于Monte carlo与基于经典阻尼最小二乘两种Rayleigh波反演策略在横波速度建模中的优缺点。

三层模型参数如表1所示，由表1中可知，横波速度较小，泊松比高达0.47，在工程物探中主要代表未固结的松散碎屑物质(如黏土层、饱和沙土等)。在高泊松比地质结构中，由于传统的PML边界条件在Rayleigh波正演数值模拟中将产生数值不稳定。基于此，采用多轴卷积完全匹配层吸收边界条件处理人工截断边界[27]，应力镜像+二阶速度展开处理自由表面边界[28]，数值模拟方法为交错网格有限差分正演模拟[29-30]。纵横向网格大小为2001×601，纵横向网格间距均为0.1 m，实际模拟区域为200 m×60 m，边界层厚度为801个网格点，时间采样间隔为0.05 ms，采样点数为60 001，总模拟时间为3 s，震源为主频8 Hz的雷克子波，震源位置位于(0，0)m，由于勘探目的层的深度应大于25 m，本算例共设置61道接收，接收点深度为0 m，第一个检波器的位置为70 m，道间距为2 m，因此最小偏移距为70 m，最大偏移距为190 m。

图2 Monte Carlo反演流程图Fig.2 Flowchart of Monte Carlo inversion

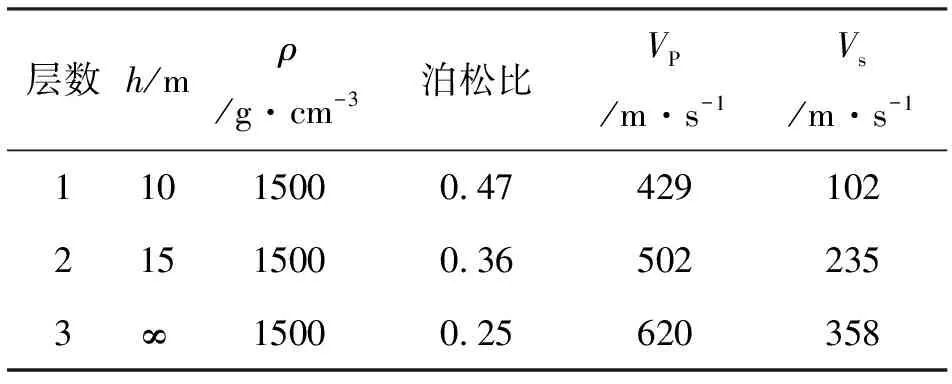
表 1 三层模型参数表

利用上述参数，通过数值模拟得到如图3所示的垂向位移分量的地震记录。从图3中可知：①地震记录中没有明显的虚假边界反射；②在时间较大时，正演模拟仍然保持稳定，这是由于本文采用了多轴卷积完全匹配层吸收边界条件；③从记录中可观察到纵波走时快、能量低，面波走时慢、能量强，呈现“扫帚状”的频散特征，表明在自由表面采用应力镜像法的处理方式是合理的。进一步，根据相移法频散曲线提取流程，以图3(a)所示的地震记录作为输入，计算得到如图3(b)所示的频散能量图，从图3中可知：①在高频部分，由于波长较短，主要受到浅部地层的影响，因此，频散能量图中的高频能量峰值主要指示浅层面波速度，数值约为96 m/s，趋近浅层横波速度的0.94倍；②在低频部分，由于波长较长，面波速度将同时受到来自浅中深地层的影响，故图3(b)中的能量峰值线能够反映深层面波速度，数值约为310 m/s，趋近于半空间横波速度的0.90倍；③如果地层情况较为复杂，则频散曲线是地下介质的综合反映。

图3 Rayleigh波合成记录及频散能量图Fig.3 Synthetic record and dispersive image of Rayleigh waves(a)垂向位移分量的地震记录；(b)频散能量图

表2 初始模型参数值

随后，从图3(b)中提取实测频散曲线作为反演的观测数据，并设计三组初始模型，前Ⅰ、Ⅱ组模型为等厚薄层模型，第Ⅲ组为非等厚薄层模型，前Ⅰ、Ⅱ组的层数均为9层，前8层厚度均为4 m，第9层为半空间，由于纵波速度及密度对Rayleigh波频散曲线影响较小，因此，纵波速度与密度设置为常数，分别为517 m/s和1 500 g/cm3。三组模型的初始横波速度设置也较为简单，并未采用复杂的拐点分层方案，而是将第I组模型的横波速度设定为线性递增速度，其中模型第1层的横波速度由频散能量图中高频能量峰值所指示的横波速度所决定，其数值为106 m/s，每层速度的增量为24 m/s，第II组设为均匀模型，横波速度值为253 m/s，第Ⅲ组模型的第一层为106 m/s，每层速度为非线性递增速度。模型参数见表2。通过对比三组初始模型与真实模型可知：两者差异较大，可用于对比检验Monte carlo反演算法与阻尼最小二乘反演算法对初始模型的依赖性与反演的稳定性。

为使反演结果达最优，第I组模型中Monte carlo反演的空间约束参数、分别为0.15、0.112 5，而第II组中、分别为0.125、0.1，第Ⅲ组中γ、δ均为0.1。经统计，第I组模型中，Monte carlo反演迭代1 000次，耗时104 s，经典阻尼最小二乘反演迭代20次，耗时122 s。而第II组模型中，Monte carlo反演迭代1 000次，耗时109 s，经典阻尼最小二乘迭代25次，耗时304 s，第Ⅲ组模型中，Monte carlo反演迭代1 000次，耗时28.8 s，经典阻尼最小二乘反演迭代10次，耗时110.7 s。实验结果表明：Monte carlo反演策略相比经典阻尼最小二乘具有较快的收敛速度。

经典阻尼最小二乘反演策略及Monte carlo反演策略从本质上来看是基于实测频散数据的拟合，为分析经典阻尼最小二乘及Monte carlo的反演质量，在三组初始模型中分别计算了经典阻尼最小及Monte carlo反演的理论频散，并进行了理论频散曲线与实测频散曲线的均方根误差分析。

图4表示在第I组等厚薄层线性递增模型中两种方法的反演结果及频散曲线的对比。为更清晰刻画在等厚薄层线性递增模型中的反演细节，图4(a)给出了经典阻尼最小二乘反演的横波速度剖面与真实模型的对比，从图4(a)中可见经典阻尼最小二乘存在如下缺点：①经典阻尼最小二乘反演法在保证反演精度的条件下，为提高反演解的唯一性，采用固定约束条件，在初始模型为等厚薄层中，层参数在每次迭代过程保持不变，减少了待反演的参数，只有横波速度作为独立变量；②在层速度突变界面，反演的横波速度剖面与真实模型存在较大差异，未能较好地评价地下介质速度结构；③对初始模型依赖性较高。图4(c)给出了Monte carlo反演的横波速度剖面与真实模型的对比，从图4(c)中可知，Monte carlo存在如下优点：①Monte carlo反演过程中采用函数约束关系寻求反演的全局最优解，即横波速度与层厚作为独立变量;②在层速度突变界面，反演的横波速度剖面与真实模型具有较小的差异，能更好地评价地下介质的速度结构;③对初始模型依赖性较低。

为进一步验证两种方法在等厚薄层线性递增模型中的反演质量。图4(b)展示了经典阻尼最小二乘反演的理论频散曲线与实测频散曲线的均方根误差，在Rayleigh波相速度100 m/s ～125 m/s区域内存在较轻微的误差(黄色框区域内)。图4(d)展示了Monte carlo反演的理论频散曲线与实测频散曲线的均方根误差。从图4(b)及图4(d)中可见，因在低频处拾取实测频散曲线存在一定误差，故两种反演算法在低频处均无法有效拟合。最后经对比，经典阻尼最小二乘反演的理论频散与实测频散的均方根误差为1.6%，Monte carlo反演的理论频散与实测频散的均方根误差为0.8%。从拟合的残差大小表明：在线性递增模型中，相比与经典阻尼最小二乘，Monte carlo反演具有较高的反演质量。

图5表示在第II组均匀模型中经典阻尼最小二乘与Monte carlo 的反演结果及频散曲线对比，为更清晰刻画在均匀模型中的反演细节，图5(a)给出了经典阻尼最小二乘反演的横波速度剖面与真实模型之间的对比，在5(a)中可见经典阻尼最小二乘存在如下缺点：①经典阻尼最小二乘为提高解的唯一性，在均匀模型中采用固定约束关系，在迭代反演中层厚度保持不变，减少了待反演的参数，只有横波速度作为独立变量；②在层速度突变界面，反演的横波速度剖面与真实模型存在较大差异，未能较好地评价地下介质速度结构；③对初始模型依赖性较高。图5(c)给出了Monte carlo反演结果与真实模型之间的对比，从5(c)中可知,Monte carlo存在如下优点：①Monte carlo在反演过程中采用函数约束关系寻求反演的全局最优解，即横波速度与层厚作为独立变量；②在层速度突变界面，反演的横波速度剖面与真实模型具有较小的差异，能更好的评价地下介质的速度结构；③对初始模型依赖性低。

为更进一步验证两种方法在均匀模型中的反演质量。图5(b)描绘了经典阻尼最小二乘反演的理论频散曲线与实测频散曲线的均方根误差。从图5(b)可知，在均匀模型中的Rayleigh波不具备频散特性，且在Rayleigh波相速度100 m/s～135 m/s区域内存在较大的误差(黄色框区域内)。图5(d)描绘了Monte carlo反演的理论频散曲线与实测频散曲线的均方根误差，红色实线表示Monte carlo反演的理论频散曲线，黄色实线表示初始模型频散曲线，黑色实线表示实测频散曲线。从图5(b)及5(d)中可见，因在低频处拾取实测频散曲线存在一定误差，故两种反演算法在低频处均无法有效拟合。最后经对比，经典阻尼最小二乘反演的理论频散与实测频散的均方根误差为2.8%。Monte carlo反演的理论频散与实测频散的均方根误差为0.9%，从拟合的残差大小表明：在均匀模型中，相比与经典阻尼最小二乘，Monte carlo频散曲线反演具有较高的反演质量。

值得注意的是，第Ⅲ组初始模型并非线性递增模型，每层的层厚度也非等厚薄层，与第Ⅰ组初始模型有明显区别。图6表示在第Ⅲ组非等厚薄层递增模型中经典阻尼最小二乘与Monte carlo 的反演结果及频散曲线对比。图6(a)为经典阻尼最小二乘反演的横波速度剖面与真实模型之间的对比，其线条的表示关系同上。在6(a)可知，经典阻尼最小二乘同样存在如下缺点：①经典阻尼最小二乘为提高解的唯一性，采用固定约束关系，在迭代反演中层厚度保持不变，减少了待反演的参数，只有横波速度作为独立变量，因此反演结果与真实模型存在较大的差异；②在层速度突变界面，由于层厚度值在反演过程中保持不变，未能较好地评价地下介质速度结构；③由于采用固定约束关系且反演过程需要利用导数信息，故初始模型的依赖性较高。图6(c)为Monte carlo反演结果与真实模型之间的对比结果。从6(c)可知，Monte carlo存在如下优点：①Monte carlo在反演过程中采用函数约束关系寻求反演的全局最优解，即横波速度与层厚作为独立变量；②在层速度突变界面，由于采用函数约束关系，能更好地评价地下介质的速度结构；③由于采用函数约束关系，故对初始模型的依赖性较低。

为更进一步验证两种方法在非等厚薄层递增模型中的反演质量。图6(b)描绘了经典阻尼最小二乘反演的理论频散曲线与实测频散曲线的均方根误差。从图6(b)可知，经典阻尼最小二乘在Rayleigh波相速度100 m/s～110 m/s区域内，存在较大的误差(黄色框内)，因此导致总体误差较大。图6(d)描绘了Monte carlo反演的理论频散曲线与实测频散曲线的均方根误差，因受低频处拾取的实测频散曲线在200 m/s～300 m/s区域的错误影响，存在较大的误差。但是从图6(b)及6(d)总体可见，因在低频处拾取实测频散曲线存在一定误差，故两种反演算法在低频处均无法有效拟合。最后经对比，经典阻尼最小二乘反演的理论频散与实测频散的均方根误差为0.9%。Monte carlo反演的理论频散与实测频散的均方根误差为0.7%，从拟合的残差大小表明：在非等厚薄层递增模型中，相比与经典阻尼最小二乘，Monte carlo频散曲线反演具有较高的反演质量。

在同台PC计算机上经对比内存消耗情况，第I组线性递增模型中，Monte carlo消耗内存1.09 GB，经典阻尼最小二乘消耗内存1.37 GB。在第II组均匀模型中，Monte carlo消耗内存1.29 GB，经典阻尼最小二乘消耗内存1.35 GB，在第Ⅲ组非等厚薄层递增模型，Monte carlo消耗内存1.13 GB,经典阻尼最小二乘消耗内存1.28 GB。实验表明基于Monte carlo反演策略在浅部横波速度结构反演中具有占用内存小的优势。

最后为验证Monte carlo反演策略的抗噪性，将实测频散曲线分别加噪0.1、0.2，利用第Ⅲ组非等厚薄层递增模型进行反演，反演结果如图7所示。

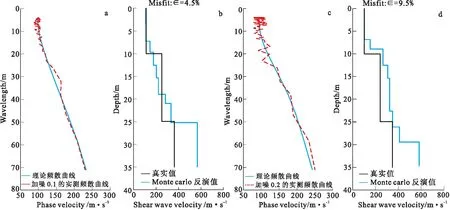
图7 Monte carl抗噪性分析Fig.7 Monte Carlo noise resistance analysis(a)Monte carlo反演的理论频散曲线与加噪0.1后的实测频散曲线对比；(b)加噪0.1后Monte carlo 反演的横波速度剖面与真实模型的对比；(c)Monte carlo反演的理论频散曲线与加噪0.2后的实测频散曲线对比;(d)加噪0.2后Monte carlo 反演的横波速度剖面与真实模型的对比

值得注意的是，由于实测频散曲线的加噪，所以反演的理论频散曲线与加噪后的实测频散曲线均方根误差ε>1%，但是从图7(b)可知，在实测频散曲线加噪0.1后，Monte carlo 反演的横波速度剖面与真实值十分接近，由图7(d)可见，Monte carlo 在实测频散曲线加噪0.2后，反演的横波速度剖面也与真实值十分接近，从抗噪实验结果表明，Monte carlo反演策略具有较好的抗噪性。

2.2 二维横波速度剖面

为精细刻画层状介质模型结构。首先，在三层层状介质模型中，模型参数见表3，通过Rayleigh波有限差分正演模拟[29-30]合成Rayleigh波多炮正演记录，为采集多炮Rayleigh波合成记录，设定观测系统为：共采集70炮数据，每炮移动4 m，第一炮震源位置为(0，0)m处，由于勘探目的层的深度应大于40 m，本算例共设置84道接收，接收点深度为0 m，第一个检波器的位置为58 m，道间距为2 m，因此最小偏移距为58 m，最大偏移距为224 m， 排列长度166 m，纵横向网格大小为501×451，纵横向网格间距都为1 m，因此模型尺寸为500 m×450 m，边界层厚度为11个网格点，采样时间间隔为0.000 1 ms，采样点数为2001，因此总时间为2 s，震源采用主频为9 Hz的雷克子波。自由边界采取应力镜像法[28]，图8为多炮面波采集示意图。将采集的多炮Rayleigh波合成记录，通过相移法提取多条Rayleigh波频散曲线。最后基于Monte carlo反演策略，对多炮Rayleigh合成记录中提取出的多条频散曲线进行自动反演。

表3 三层模型参数表

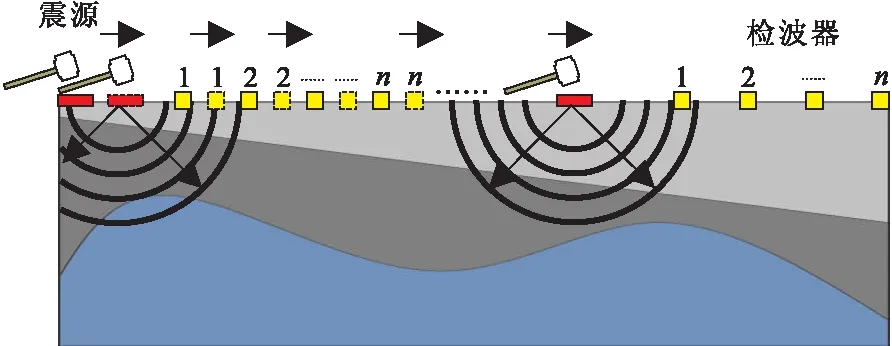
图8 多炮面波采集示意图Fig.8 Schematic diagram of multi-shot surface wave collection

将采集到的多炮合成记录根据相移法提取频散曲线，以图9(a)所示的炮记录作为输入，计算得到如图9(b)所示的频散能量图，沿能量峰值线拾取实测频散曲线得到图9(c)。每一炮地震记录均可产生频散能量图，可沿能量峰值线拾取每一炮地震记录的实测频散曲线。

图9 第一炮Rayleigh波合成记录及实测频散数据Fig.9 Rayleigh-wave synthesis record and measured dispersion data of the first shot(a)垂直位移分量的地震记录；(b)频散能量图；(c)实测频散曲线

根据拾取出的70条实测频散曲线，反演其相速度，可得到各70炮炮集排列中点处所对应的横波速度随深度的变化曲线，根据一系列变化曲线可得到二维横波速度剖面。为验证Monte carlo在70炮中的反演质量，现从70炮合成记录中抽取第25炮合成记录，根据相移法拾取实测频散曲线，最后利用表4所示的初始模型参数值进行反演，迭代次数共1 000 次，为使Monte Carlo反演法能在众多局部最优解中寻求全局最优解，因此设置横波速度与层厚的空间约束参数、分为0.37、0.38。

表4初始模型参数值

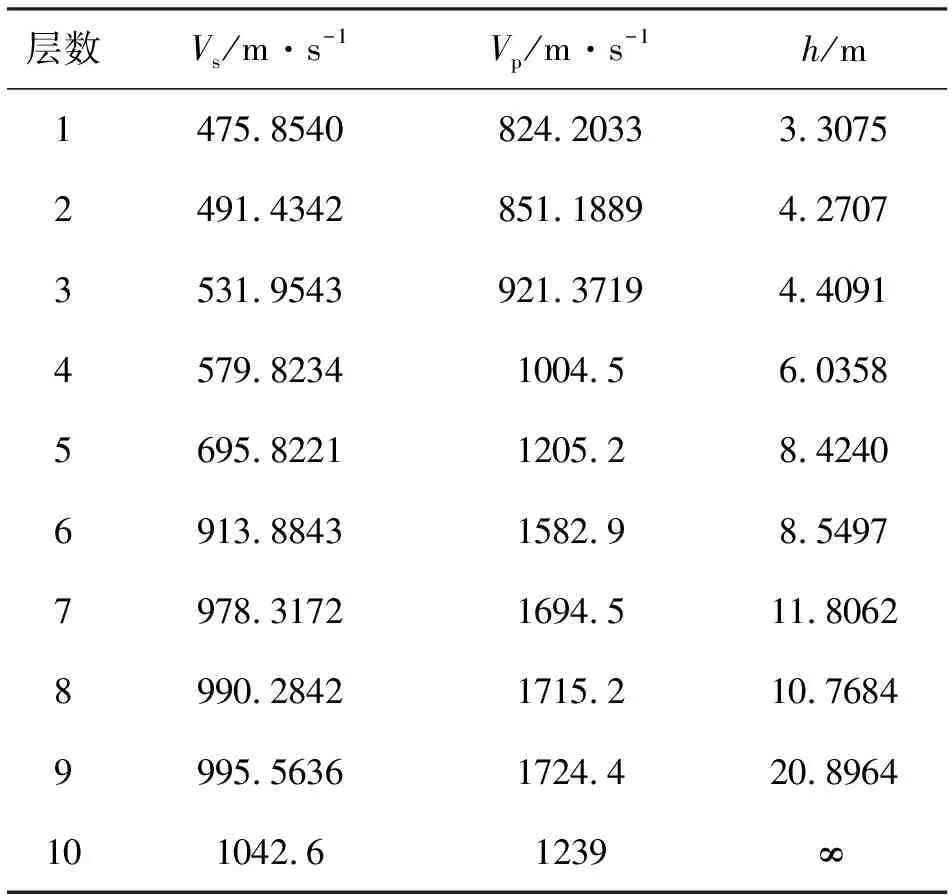
表 5 第25炮反演结果统计表

在空间约束参数、所确定的随机样本空间中，每一个随机样本空间对应每一个模型参数值，将每一个模型参数值正演一次，并与实测频散曲线计算均方根误差，反演结果如图10所示，图10(a)为Monte carlo反演的理论频散与实测频散的均方根误差，最小均方根误差为0.6%。图10(b)表示Monte carlo反演的横波速度剖面与真实模型的对比结果，最小均方根误差为0.6%。表5为均方根误差达0.6%时的反演结果。

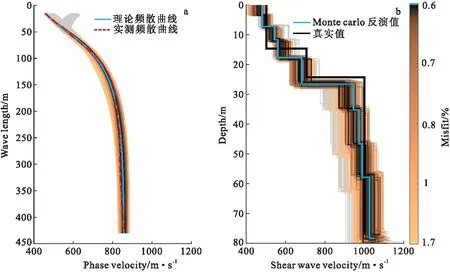
图10 排列中点为141 m处的反演结果Fig.10 Inversion results of the permutation midpoint at 141 m(a)Monte carlo反演的理论频散与实测频散的对比；(b)Monte carlo反演的横波速度剖面与真实模型的对比

在第25炮频散曲线反演中耗时共计79.846 s，误差0.6%，表明在迭代1 000次中，Monte carlo反演法收敛速度快，误差较小，具有较好的反演质量。

提取70炮的实测频散曲线，根据表4初始模型参数值利用Monte carlo自动反演，可得到二维横波速度剖面。图11表示Monte carlo在提取的70条频散曲线中自动反演的结果并与真实模型之间的对比，从图11反演对比结果上来看，Monte carlo反演剖面与真实模型基本吻合，表明基于Monte carlo反演策略在浅地表横波速度反演中具有良好的反演质量，能较好刻画模型的精细结构。

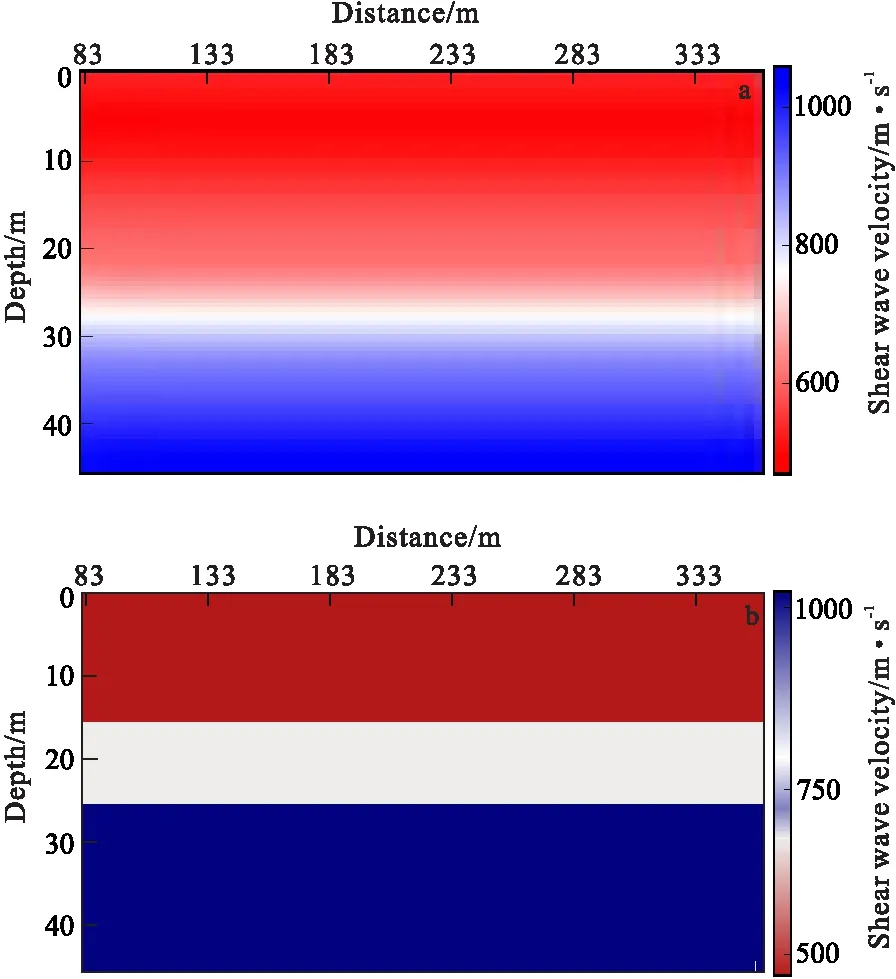
图11 Monte carlo反演的横波速度剖面与真实模型对比结果Fig.11 Shear wave velocity profile of Monte Carlo inversion and comparison with the real model(a)Monte carlo反演结果；(b)真实模型

2.3 Monte carlo实际应用案例

测试点位于贵州大学西校区图书馆前，如图12中红色实线所示。为在测试点构建地下二维垂直横波速度场，采用工程地震仪WZG-24A进行Rayleigh波数据采集，炮激发源采用重5 kg的大锤敲击0.2 m的铝板作为冲击激发。共采集17炮数据，第一炮震源位置为(0,0)m，采用12道检波器线性排列接收信号，检波器深度为0.1 m，最小偏移距为6 m，最大偏移距为28 m，道间距为2 m，因此排列长度为22 m，沿测线方向以2 m的间隔不断移动震源及检波器位置。根据MASW原理，在该观测系统下可测定17 m～49 m范围内的地下介质情况。

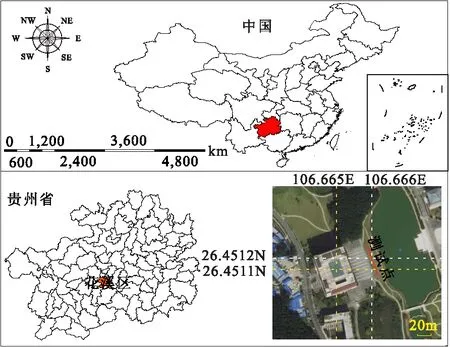
图12 现场测试示意图Fig.12 Field test diagram

沿测线方向并根据多炮面波数据采集，共采集17炮数据，图13所示为该测试点沿测线采集的第6炮及第12炮的炮集记录。从图13的炮集记录中可见Rayleigh波信噪比最高，能量最强，占据主导地位。

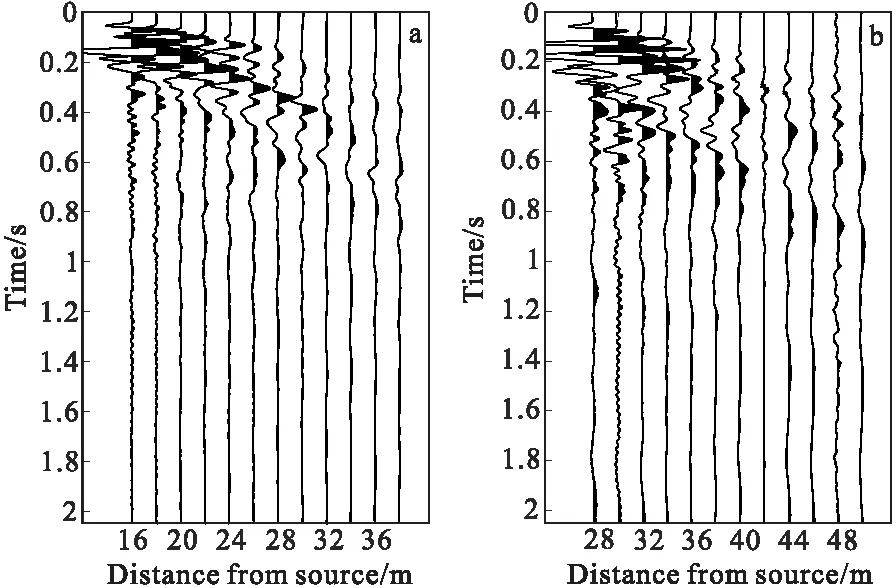
图13 测试点获取的面波记录Fig.13 Typical surface wave records obtained at the test site(a)第六炮炮集记录;(b)第12炮炮集记录

进一步，根据第6炮炮集记录及第12炮炮集记录，利用相移法提取Rayleigh波实测频散曲线，根据实测频散曲线的形态特征初步估计初始模型。初始模型参数估计如表6所示。

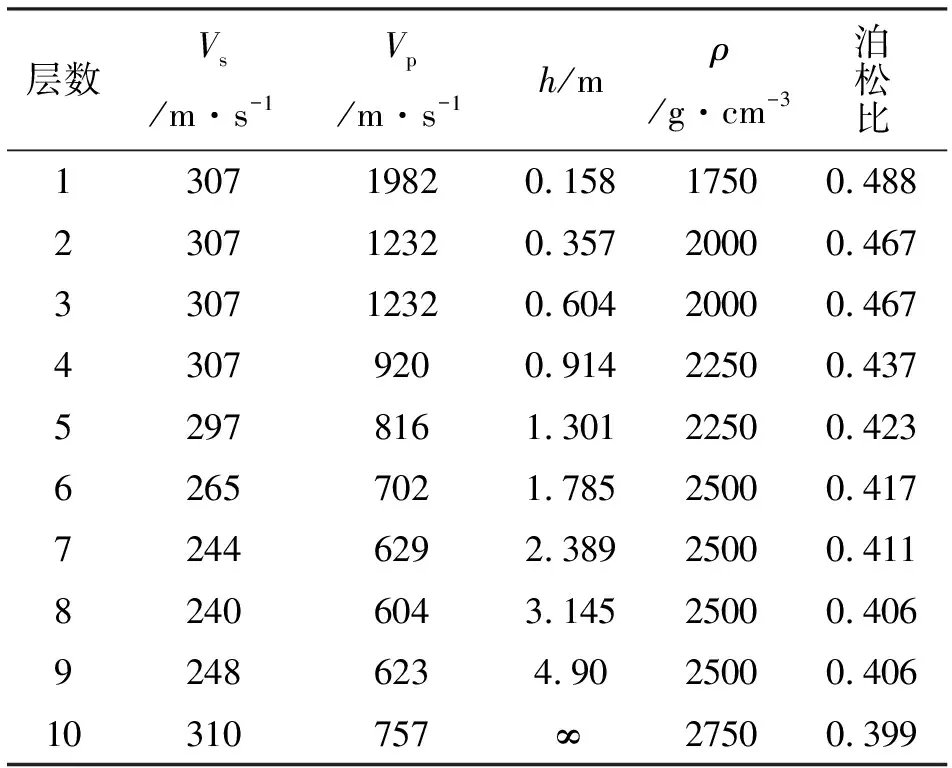
表6 初始模型参数Tab.6 Initial model parameter values

最后根据初始模型参数值，采取Monte carlo反演策略反演其相速度，可得到该排列中点所对应的横波速度剖面(图14)。图14(a)为从第6炮炮数据中提取频散曲线并反演其相速度，所得到的排列中点为27 m的横波速度剖面，图14(b)为从第12炮炮集记录中提取频散曲线并反演其相速度，所得到的排列中点为39 m的横波速度剖面。

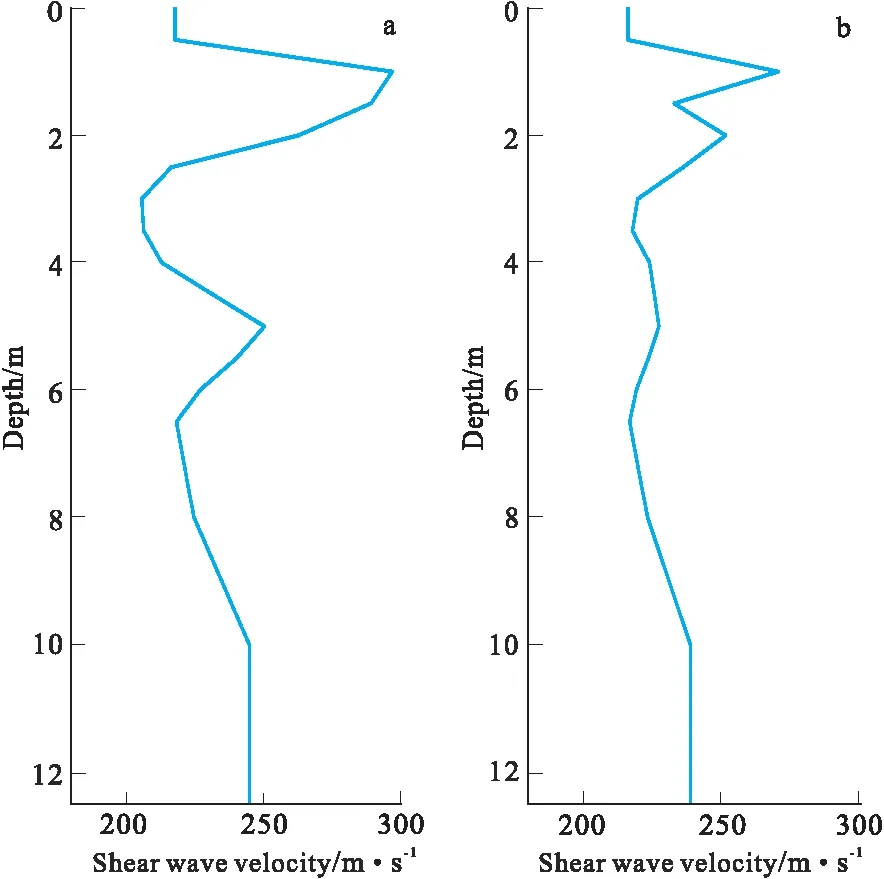
图14 Monte carlo 反演的横波速度剖面Fig.14 Shear wave velocity profile by Monte Carlo inversion(a)排列中点为27 m的反演结果;(b)排列中点为39 m的反演结果

根据一系列反演的横波速度剖面并排列，可得到该测试点所测试的17 m～49 m范围内的二维横波速度剖面，如图15所示。

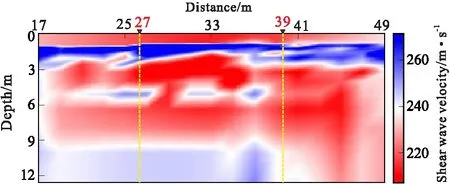
图15 测试点的二维横波速度剖面Fig.15 2D shear wave velocity profile obtained at the test site

图15中，两条黄色虚线分别代表图14(a)中27 m处反演的横波速度剖面，图14(b)中39 m处反演的横波速度剖面。从图15中总体可见，该地下介质在深度为0 m～1.5 m处，横波速度值较小，从现场的推断上来看上层覆盖物应为第四纪松散的土质层。而深度为1.5 m～2.8 m，横波速度值较大，应推断该处为岩石层。深度为2.8 m～9 m处的横波速度值总体较小，5.5 m～6 m处局部横波速度又较大，故推断该深度下应为黏土层，局部夹厚度约为0.5 m的岩石层。

4 结论

笔者在求解水平层状介质中Rayleigh波的本征值问题之上发展了Monte carlo局部线性化反演算法，在典型数值模型中，通过三组初始模型参数值分别用基于经典阻尼最小二乘与基于Monte carlo两种反演策略进行频散曲线反演，并用反演的理论频散与实测频散进行均方根误差对比分析，可得到如下认识。

1)基于经典阻尼最小二乘反演策略在反演过程中采用固定约束，未能较好地评价地下介质速度结构，且在反演过程中需利用导数信息，所以对初始模型依赖性较高，而基于Monte carlo反演策略采用函数约束关系，能较好地评价地下介质速度结构，且不需要利用导数信息，故对初始模型依赖性低，在反演过程中也较为稳定，并具有较高的反演精度。

2)Monte carlo反演策略在实测频散曲线加噪0.1、0.2后仍然具有较高的反演精度，表明Monte carlo 反演策略具有较好的抗噪性。

3)在同台PC计算机条件下，相比于经典的阻尼最小二乘，Monte carlo反演策略具有较快的收敛速度和反演质量。

4)在多条Rayleigh波频散曲线自动反演中，基于Monte carlo反演的二维横波速度剖面与真实模型也较为吻合，能较好地刻画地质模型的精细结构。

虽然基于Monte carlo频散曲线反演具有较高的计算效率，但是在低速半空间、高速表层、横向不均匀介质模型等复杂模型中该算法存在适用性较低等缺点。因此在今后的研究中，将Monte Carlo反演算法应用于低速半空间、高速表层、横向不均匀介质等复杂模型的横波速度建模中是下一步的研究重点，特别是针对Monte Carlo反演算法存在分辨率低，在未知层厚的情况下，适用性变差等缺陷，有待进一步研究。