基于粒子群支持向量回归优化的循环流化床床温预测分析

黄纯颖，曾庆敏，陈玲红，吴学成，岑可法

（浙江大学 能源清洁利用国家重点实验室，浙江 杭州 310027）

0 引 言

循环流化床（circulating fluidized bed，CFB）具有负荷调节快、脱硫效率高、污染排放低等优点，近年来一直是能源清洁利用的重要技术[1]。 CFB的最大特点是整个燃烧过程中的流动状态，在燃烧期间气体作为流动介质，许多固体燃料和床料在炉中燃烧从而产生许多小颗粒的飞粉，循环灰分离器将飞出的灰粉通过管道送回炉中再次燃烧以此保证燃烧效率。 此外炉中反复进行低温燃烧和等级燃烧，最终提高了脱硫效率[2]。 因此，大力发展CFB燃烧技术，研究相应的优化控制方式也是一大趋势。

CFB锅炉与常规煤粉炉另一大差别是其独特的控制系统，特别是锅炉床温的控制。 CFB的床温水平对于锅炉燃烧安全性与经济性会产生极大影响。 除此之外，考虑脱硫效果的最佳床温运行区间在850 ～900℃，温度过低，石灰石煅烧速度显著下降；温度过高，脱硫产物CaSO4会在还原性气氛中被大量分解[2-4]。 CFB的床温运行系统具有非线性、参数时变和多变量耦合等特性，故极难通过简单机理建模来进行预测控制研究[5]。

对于CFB锅炉这样复杂的燃烧系统的控制，重要的是建立一个可以准确反映其燃烧系统对象特性的模型。 目前床温特性建模主要有以下几种方法：（1）通过大量的现场试验收集数据，根据试验数据建立回归关系，这种方式需要花费一定的人力、物力成本，试验工况的种类也会有局限性[6]；（2）根据CFB锅炉系统物理或化学变化规律进行机理建模，这是最原始的床温建模法，可以从原理角度反映床温变化趋势，但机理模型往往存在需要合理的简化假设，无法保证在各个工况下的预测精度[7]；（3）利用计算流体力学、传热学等机理模拟炉内燃烧过程，求得炉内床温分布情况，这种方法从精确度来说较第二种已有了很大的提高，且被证实有良好的效果[8]，但由于其涉及到复杂的机理建模和计算步长，需要高端的计算机配置及较长的计算时间才能够完成建模的全过程，经济性不高[9]。 此外，由于CFB锅炉运行时有入炉组分复杂、多边形强等特点，给CFB的传统建模方式带来了困难，这就需要CFB床温特性建模需要有较好的自适应能力，而这项能力是以上三种方式所欠缺的。

随着科学技术及人工智能的发展，电厂的分散控制系统也日益完善，基于神经网络（artificial neural networks，ANN）及支持向量回归（support vector regression，SVR）对电厂燃烧特性进行预测建模的方法得到广泛的关注及研究。 基于电厂大数据进行建模时，SVR应用了结构性风险小化（structure risk minimization，SRM）原则，在非线性和高阶模式识别的解决中展示了其独特的优点，并且与ANN相比泛化能力更强[10，11]。 同时，SVR引入了可以将输入空间映射到相应的特征空间的核函数，从而对样本数据在高维特征空间建立非线性模型，即可以使用核函数将影响床温变化的因素数据向高维空间映射，提高预测模型的精度。廖伟等指出，支持向量回归不再使用传统的经验风险最小化原则，同时最小化学习算法的失灵敏度损失系数ε是Min-Max理论中均值绝对误差准则的推广，该理论具有较强的能力[12]。

本文研究对象为某热电厂130 t/h CFB锅炉，整体床温模型设计如图1 所示。 首先，从控制运行的角度出发，确定该锅炉的床温影响因素，基于该电厂分散控制系统整合而得的CFB锅炉数据样本，对样本数据进行清洗后，再进行数据预处理及归一化操作，接着利用不同的特征选择方法对输入变量进行处理，以此来提高模型预测准确性，同时使用粒子群算法（particle swarm optimization，PSO）对模型参数进行寻优，进一步提高预测准确性及模型适用性，在此基础上利用SVR对该CFB锅炉床温进行回归预测，从而实现对电厂床温的预测控制研究。

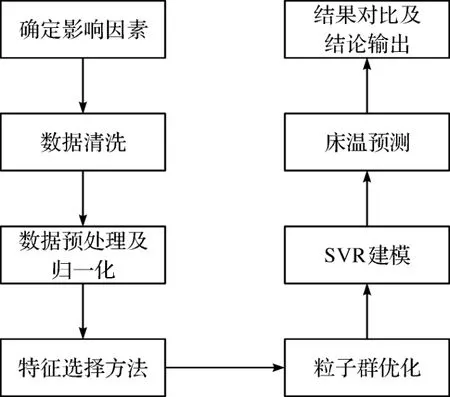
图1 床温模型设计流程图

1 锅炉概况

本研究130 t/h CFB锅炉为单锅筒、自然循环、集中下降管、∏型布置、单级高温分离循环系统的循环流化床锅炉，采用半露天布置。 锅炉由一个膜式水冷壁炉膛、两个汽冷式旋风分离器和一个尾部竖井烟道及其上的蒸汽包墙组成。 运行时过热蒸汽采用锅炉给水喷水减温。

其炉膛结构与物料入炉位置如图2 所示，两个给煤口与两个石灰石口均位于炉膛前墙。 各床温测点如图3 所示，前后墙分别有4 个测温点，测点均在炉膛下方密相区。

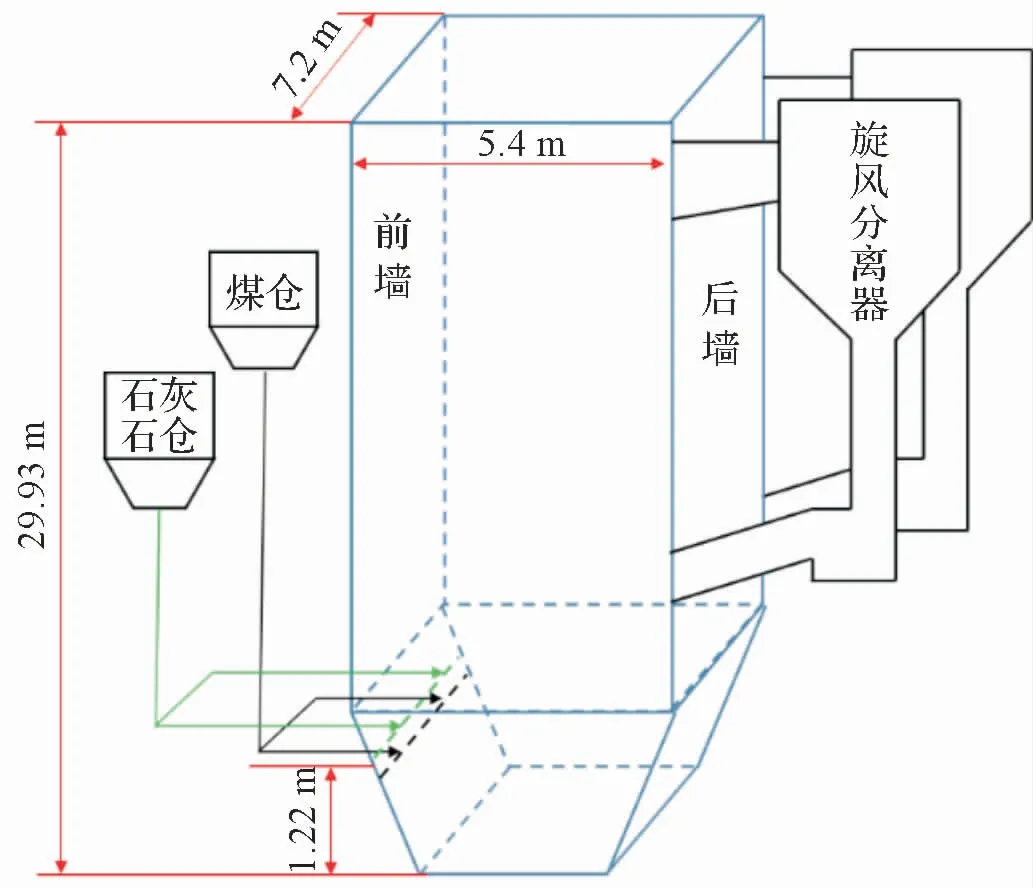
图2 CFB锅炉结构图

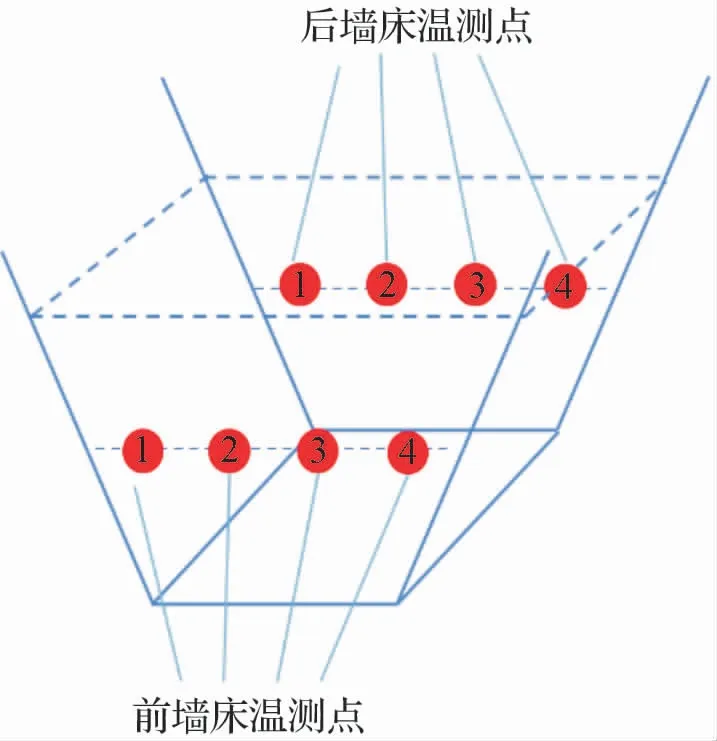
图3 CFB锅炉密相区床温测点示意图

2 建模原理

2.1 支持向量回归原理

SVR是在支持向量机（support vector machine，SVM）的基础上发展而来的，最开始SVM 主要被应用于分类问题，后来SVR被逐渐应用在回归估计中。

SVR模型建立的基本思想：通过一个非线性映射将训练集和样本集的输入参数映射到高维特征空间，在此特征空间中利用以下公式进行线性建模：

式中：σ为宽度参数，对径向作用的范围进行控制。

2.2 粒子群优化算法原理

PSO优化算法是一种进化计算技术，它的特点是简单、快速及高效，在人工智能及深度学习方面有极大的应用潜力。 PSO与遗传算法类似，是一种以群体为基础的优化工具，不同的是PSO不需要进行交叉和变异的操作，而是粒子在解空间自行迭代搜寻最优解。

PSO的算法流程如下。

（1）初始化

首先，设置最大迭代次数、粒子最大速度、目标函数自变量个数及搜索空间的位置信息，之后随即初始化速度、位置及粒子群规模。

（2）搜寻全局最优解

从每个粒子找到的最优解，即个体极值中，搜寻到一个全局最优解，并与历史全局最优比较后进行更新。

（3）更新速度和位置公式

式中：ω为惯性因子，其大小决定了PSO算法的寻优性能；C1和C2为加速常数，一般取C1=C2∈[0，4]；Xid为第i个变量在第d 维的当前位置；Vid是第i个变量在第d 维的速度；Pid为第i个变量在第d 维的个体极值点的位置；Pgd为整个种群在第d 维的全局极值点的位置。

（4）终止条件

当达到最大迭代数或相邻两代偏差位于指定范围内时，搜寻停止。

寻优过程可简化为如图4 所示：

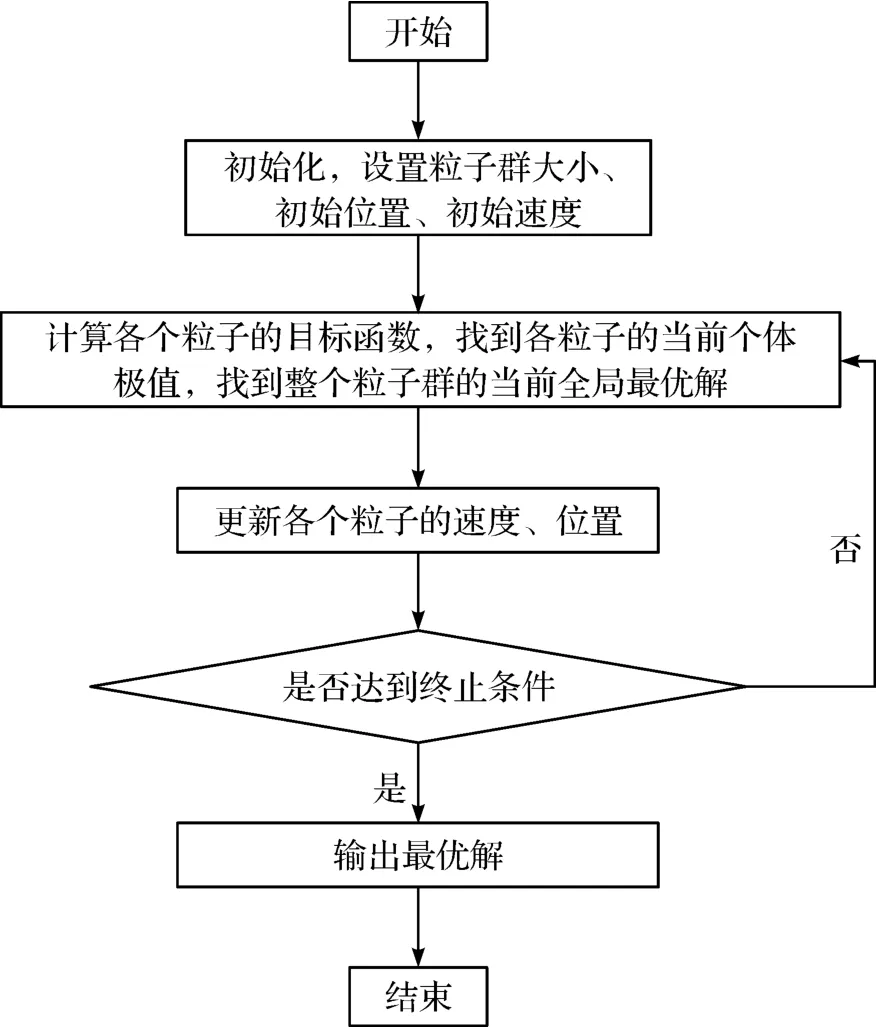
图4 粒子群寻优路径

3 模型建立

3.1 变量选择

CFB锅炉床温是由多变量耦合作用影响的对象，有研究表明，CFB床温的影响因素可总结为运行负荷、一次风量、二次风量、给煤等[13]，锅炉在正常工况下运行时，通过对以上因素的调整可以进行床温控制，本研究在以上影响因素的基础上，加入引风机电流、石灰石入炉频率等可调节参数及其他影响参数，拓宽变量选择范围，以某热电厂130 t/h CFB锅炉为研究对象，使用表1 中所列参数作为因变量，利用DCS 系统数据对于床温变化水平进行实时建模。

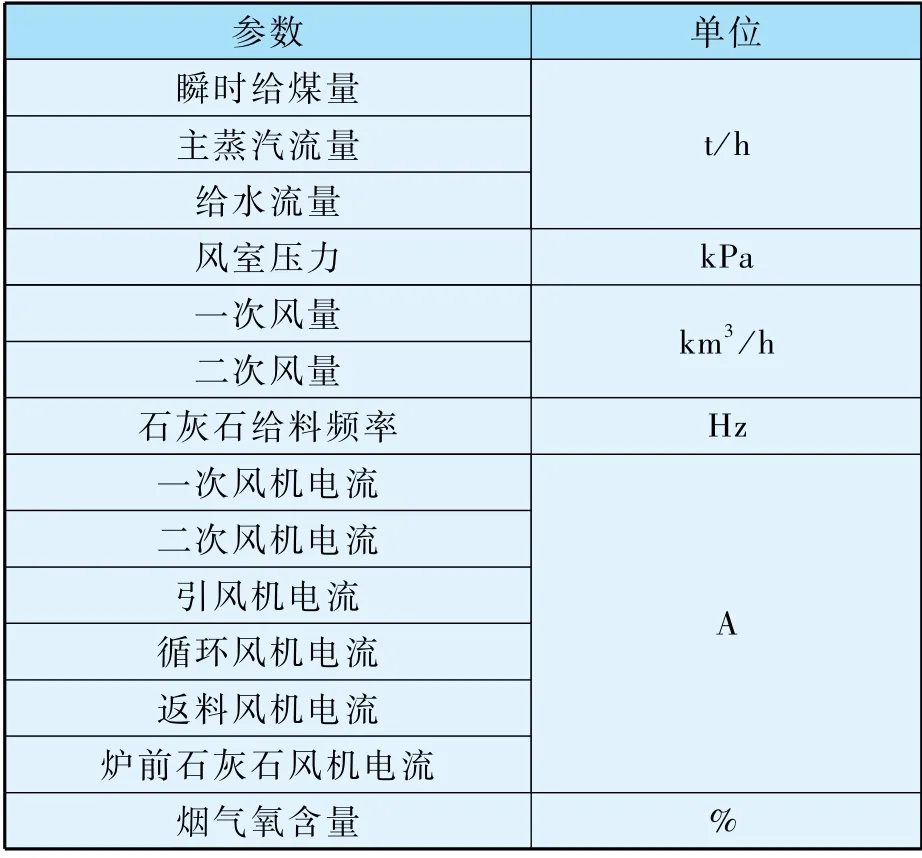
表1 变量选择清单

3.2 数据预处理——归一化

选取某热电厂DCS 系统中2020 年8 月1 日0：00 至2020 年10 月12 日24：00 共2348 条数据，首先对异常值、空值等进行清洗处理，经过数据清洗操作后筛选出表2 中的2166 条数据进行进一步研究。

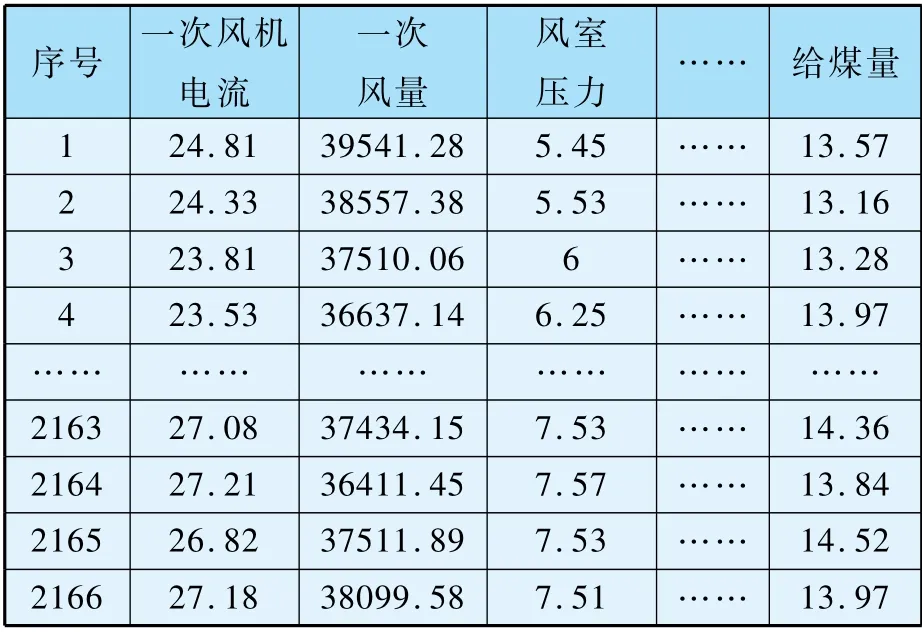
表2 热电厂DCS 数据

在进行特征选择及建模之前，为了避免参数间量纲以及数量级的不同造成模型性能的降低，接着对筛选清洗完毕的热电厂月运行DCS 数据执行归一化操作。 通过归一化操作可以把数据映射到[0，1]之间，从而消除各大特征的量纲对最终模拟结果的影响。 归一化变化的函数为：

3.3 特征选择

数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限。 好的特征选择能够提升模型的性能，更能帮助理解数据的特点、底层结构，这对进一步改善模型、算法都有着重要作用[14]。故在本文分析中，选择合适的特征来帮助建模是有必要的，这有助于提高模型预测的准确性，并为后续优化研究工作的进一步开展提供参考。

3.3.1 互信息法

互信息（mutual information，MI）数值结果表示两个变量（如X与Y）是否具有变化关系，及其关系的强弱，其常用于非线性建模中的变量筛选。如果（X，Y） ～p（x，y），X，Y之间的互信息I（X；Y）定义为：

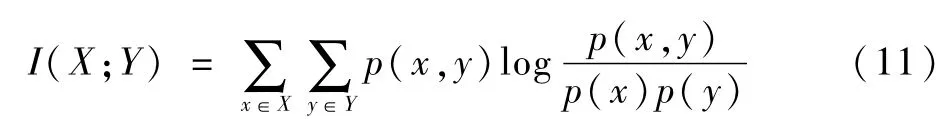
利用互信息法对特征进行处理后，各特征排序如图5 所示，根据表3 互信息值与相关程度的关系，互信息值越接近1，两个变量间的关联性越强。 故为了保证模型效果及预测准确性，在以上可调节CFB锅炉参数中根据互信息值大小进行筛选，将关联性较高，即选择大于0.2 的共11 个特征进行进一步研究。

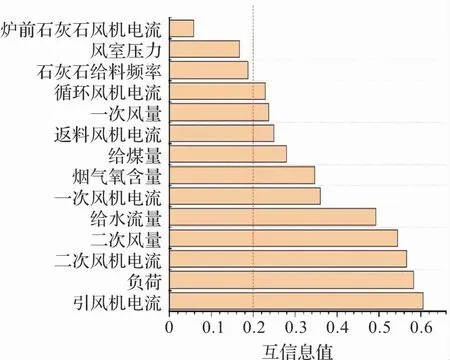
图5 各参数互信息值

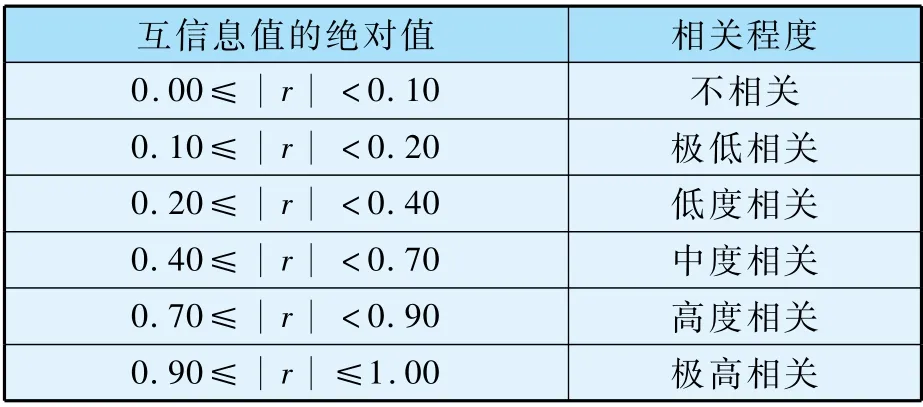
表3 互信息值与相关程度关系[15]

3.3.2 主成分分析法

主成分分析（principal component analysis，PCA）是一种常用的数据分析方法，可以识别影响过程监控参数变化的主要因素或大量过程变量中指标的下降，通常可以用来降低高维数据空间的维数。另外，PCA是基于原始数据空间的，它通过构造一组新的变量来降低原始数据空间的维数，然后从新的映射空间中提取主要的变化信息，提取统计特征，从而构造出原始数据空间特征的新解[16]。

对14 个参数变量进行PCA分析，选取累计贡献率为80%以上的成分作为主成分，最终得到四个主成分结果（见图6）。

图6 主成分分析结果

3.4 参数优化

将源数据随机划分为训练集与测试集，其中训练集占75%，测试集占25%。 训练最终模型前，为了使模型达到最佳性能，需要确定SVR算法中的惩罚系数C和径向核函数g，针对以上两种特征选择方法，本文使用PSO算法进行优化参数选择。

使用matlab 软件，在一定范围内基于PSO方法对C和g 参数进行取值。 将训练集作为原始数据进行关于C和g 参数的计算，选择准确率最高的一组作为最终的最佳参数。 当存在多组准确率高的C和g 参数的组合时，则选择C值最小的参数组合，若存在多组C值最小组，则选取搜索到的第一组C和g 参数，通过这样的参数选取方式，可以避免机器学习过程中产生过学习的状态，从而降低模型的泛化能力[17]。

基于上述参数选取规则，进行PSO算法寻优过程后，分别得到不同特征选取方式下的适应度变化趋势结果如图7 和图8 所示，对于MI法则得到的最优参数组合为：C=4.7682，g =1.4134；对于PCA法则得到的最优参数组合为：C=0.1000，g =6.0163。 故对于不同的特征选择方式来说，寻优得到了不同的组合结果，为避免机器学习机制的过学习状态，在寻优过程中通常选取较小的惩罚参数C值[18]。

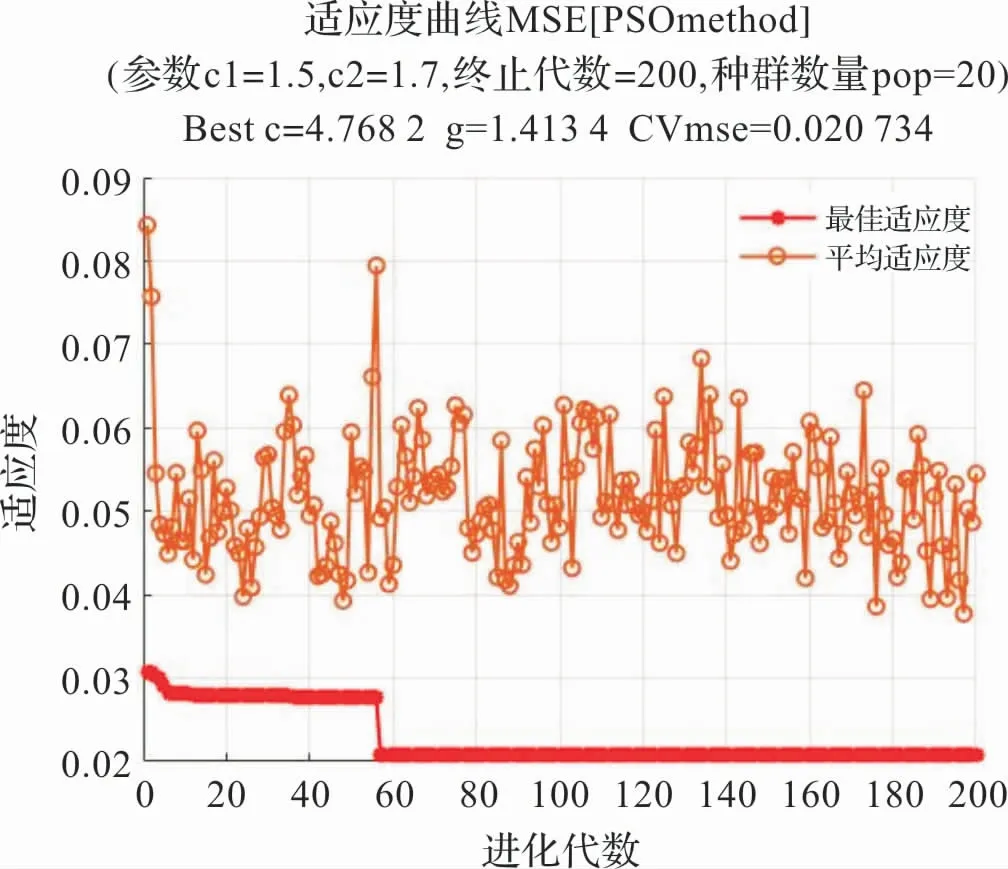
图7 互信息法寻优结果

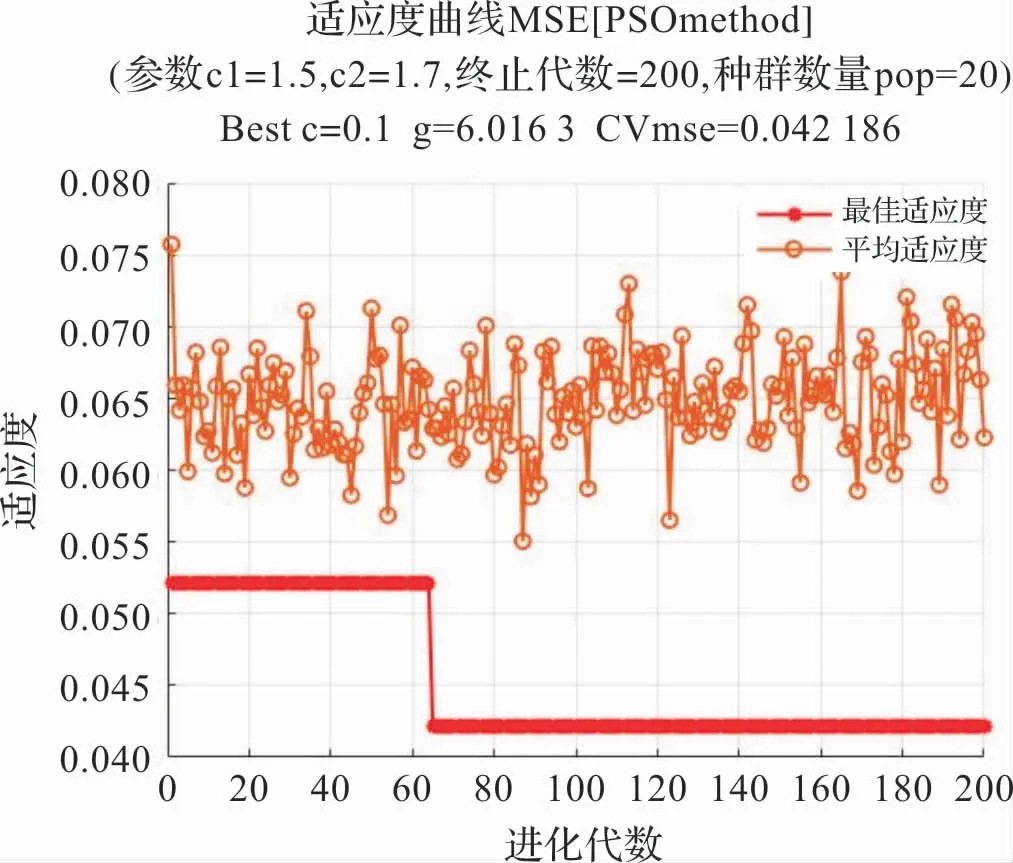
图8 主成分分析寻优结果

3.5 模型仿真结果

在对比仿真结果之前，引入指标评价体系评估模型效果：

在进行特征选择及粒子群参数寻优后，最终模型仿真结果如图9 -图11 所示。 由仿真图形可以得出，经过互信息化特征选择的PSO-SVR模型拟合结果与实际床温结果更为接近，即该MI-PSO-SVR仿真模型能够对该锅炉床温变化情况做出准确预测。 由表5 的模型评价指标可知，MI-PSO-SVR的模型均方根误差仅4.37，相关系数平方高达0.9189， 绝对百分比误差低至0.38%。相反，经过PCA分析处理过后的模型呈现出较差的拟合水平，仿真结果的均方根误差高达11.52，相关系数平方仅为-0.2219，MAPE高达1.04%，可被认为是劣质模型。

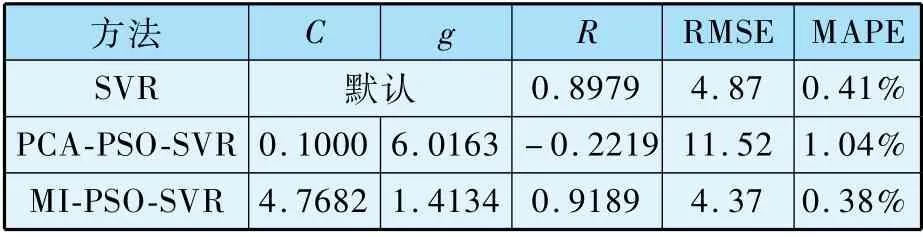
表5 模拟仿真结果汇总表

图9 SVR仿真结果

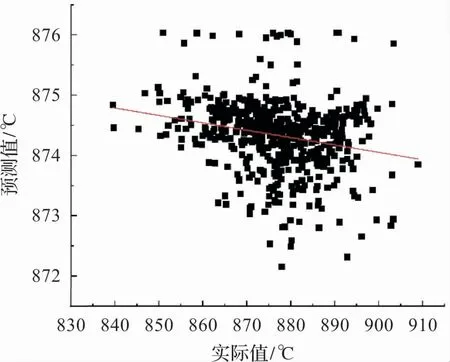
图10 PCA-PSO-SVR仿真结果

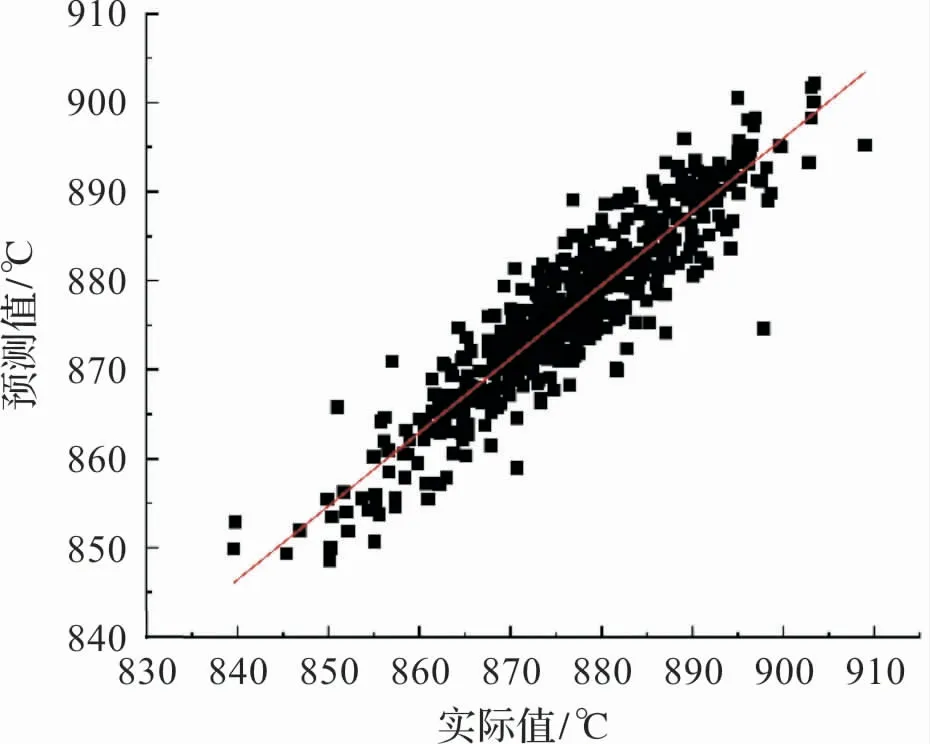
图11 MI-PSO-SVR仿真结果

4 结 论

对于由相互耦合的多变量控制影响的CFB锅炉燃烧系统，为完成精准建模预测及控制，本文研究了某热电厂130 t/h CFB锅炉床温运行状况，结合其实际运行数据，在基于研究经验及机理原理所选择的床温影响因素的基础上，加入了更多可调节参数，最终完成了该CFB锅炉运行床温预测模型的建立，为锅炉床温优化控制奠定了基础。

本文对比了不同特征选择方法下的建模精准性，结果表明，使用MI法则处理可以有效提高模型预测结果准确性，这也表明，在利用优化算法提高预测效率同时，输入参数的选择也十分重要。参数选取的合理性有助于减少欠学习或过学习的现象，从而帮助预测精度获得提升。 然而，被广泛使用的PCA法则不适用于本文的SVR建模过程，这是由于该特征选择方法在执行过程中令原DCS 数据集结构产生丢失所致。

通过本文研究得到，MI法则进行数据预处理并利用PSO算法优化后的SVR模型能够精确地预测在不同运行工况下的床温，且预测误差较小，拥有较强的泛化能力。