基于ColBert-EL 和MRC 模型的零样本实体链接
王雪莹,程路易,徐 波
(东华大学 计算机科学与技术学院,上海 201620)
0 引言
实体链接任务的目标是将文本中的实体指称项链接到知识库中对应的实体,是许多信息抽取和自然语言理解等应用的重要组成部分,因其解决了命名实体的词汇歧义。传统的实体链接解决方案通常假定在测试中要链接的实体在训练过程中已经见过,但是在实际应用中,这种假设往往并不成立。要链接的实体往往在训练集中没有出现过,并且每个实体也没有很多的结构化先验信息,如别名表、先验概率、结构化数据等,仅有一段关于实体的摘要信息。这种情况被称为零样本实体链接。
当前零样本实体链接方法主要采取两阶段的策略,如图1 所示,第一阶段是候选实体生成,其目标是快速找到文本中实体指称项在知识库中的候选实体集合;第二阶段是候选实体排序,其目标是对候选实体进行精准的重排序,并返回得分最高的实体作为指称项匹配的实体。然而,这些方法主要存在2 个问题。第一个问题是在候选实体生成阶段,由于过分追求效率,对指称项所在文本和实体摘要进行单独编码,没有充分考虑两者之间的交互,导致召回率不高;第二个问题是在实体排序阶段,只是单独地考虑了每个候选实体和指称项的关系,未将所有候选实体作为一个整体进行考虑,这在一定程度上影响了整体的精度。
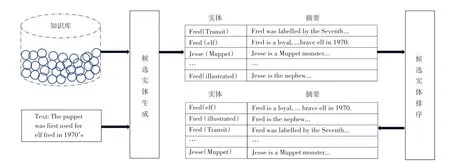
图1 两阶段零样本实体链接方法Fig.1 Two-stage zero-shot entity linking method
综前问题所述,本文提出了一种基于ColBert-EL 和MRC 模型的零样本实体链接方法。在候选实体生成阶段,针对指称项所在文本和实体摘要缺乏交互的问题,提出了一个基于ColBert的变种方法-ColBert-EL,既可以让指称项所在文本和实体摘要进行充分交互,又可以快速地检索。在候选实体排序阶段,针对所有候选实体没有整体考虑的问题,本文将其建模成一个多项选择问题,并提出了一个基于机器阅读理解的模型来对结果进行统一排序。
研究中,在公开的零样本实体链接数据集ZESHEL上进行了实验,与基线方法的结果相比,在候选实体生成阶段,召回率提升了5.9%,在候选实体排序阶段,准确率提升了4.12%。实验结果验证了本文提出方法的有效性。
1 相关工作
零样本实体链接可以分为候选实体生成和候选实体排序两个阶段。在候选实体生成阶段,主要分为基于词义的方法和基于语义的方法。例如,文献[6]中使用BM25 基于词义的方法来生成候选实体。但这种方法存在词汇不匹配问题,这会导致模型在一开始就把正确答案排除在外,导致召回率过低,在后一阶段即使使用复杂的模型也无法找到正确答案。文献[7]中使用了BERT 等基于语义的方法来生成候选实体。基本思路是将指称项所在文本和实体摘要使用BERT 进行单独编码,最后计算两者的相似性。然而这种方法没有充分考虑两者之间的交互,依然会导致召回率不高。
在候选实体排序阶段,目前的零样本实体链接方法主要采用Cross-encoder 的方法进行重排序。研究时将实体指称项所在文本和每个候选实体的摘要进行拼接后,利用Bert 编码器得到拼接后句子的编码,再通过一个全连接层输出匹配的分数。最后取所有候选实体中分数最大者作为当前实体指称项应该链接的实体。但是这种方法是单独考虑每一个候选实体的,在整体的精度上的表现有待加强。
2 方法
2.1 任务定义
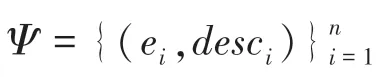
2.2 候选实体生成
本文提出了一种基于ColBert的变种方法-ColBert-EL 用于生成候选实体。ColBert 最早用于信息检索领域,主要用于估计查询和文档的相关性。其基本思路是先对文本中的每个词向量和实体摘要中的每个词向量进行独立编码,然后采用一种后期交互(Late Interaction)的方式来计算指称项和候选实体的相似度,考虑到了匹配的效率,又让文本和摘要进行了充分交互。本文对其原始模型的输入进行了重新设计,使其能够用于实体链接任务。ColBert-EL模型结构如图2 所示。
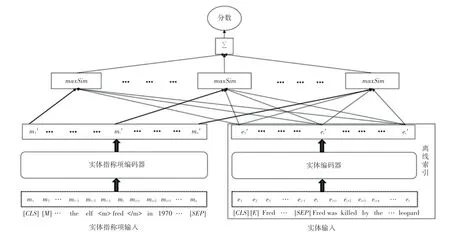
图2 ColBert-EL 模型结构图Fig.2 Structure diagram of ColBert-EL model
对于每个实体指称项,其具体表示形式为:
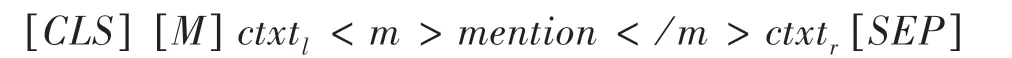
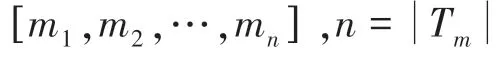
实体及其摘要的具体输入形式为:
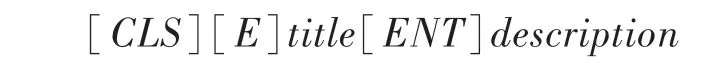
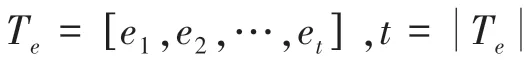
得到实体指称项和实体相关词向量的编码后,编码器将输出编码通过一个没有激活函数的线性层。该层减小每个词向量编码的输出维度,使其小于Bert 编码器的隐藏层维度,用于控制ColBert-EL的计算成本。最后,每一个输出编码将会用范式被归一化。这样做的优点是任意2 个编码的点积的结果将落在[-1,1]范围内,等同于两者的余弦相似度。
综上,当给出T=[,,…,m],T=[,,…,e]后,得到实体指称项和实体编码的方式如下:
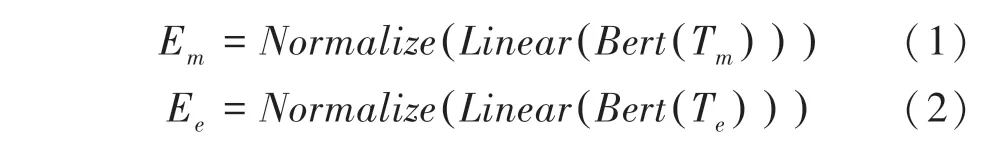
当得到实体指称项和实体相关信息的编码后,利用公式(3)计算实体与当前实体指称项的相关性分数:
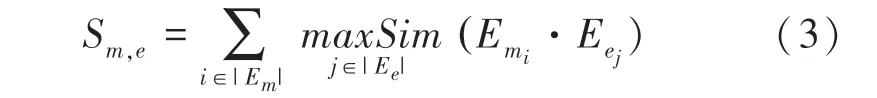
也就是,先计算实体指称项的每一个词编码与实体所有词向量编码的余弦相似度,选出最大者作为实体指称项当前词编码的最大相似度分数。将实体指称项每一个词编码的最大余弦相似度分数相加,便得到当前实体与实体指称项的相关性分数。
2.3 候选实体排序
候选实体排序的目标是对实体指称项的每个候选实体进行重新排序,选出与实体指称项相关性最大的候选实体,并将其当作实体指称项应该链接的实体。该过程的输出结果直接决定了整体框架的好坏。因此,本文使用了一个基于机器阅读理解(MRC)的模型来充分考虑指称项文本和候选实体摘要之间的交互,并且考虑了全部的候选实体。MRC 模型结构如图3 所示。

图3 MRC 模型结构图Fig.3 Structure diagram of MRC model
具体来说,对于每一个候选实体,研究将实体的摘要信息和指称项所在文本进行拼接,拼接结果如下所示:
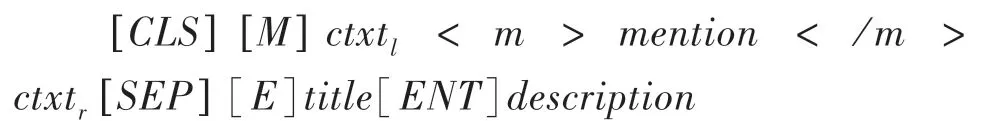
这种输入形式使得实体指称项和候选实体的信息通过编码器得到更深层次的交互,更好地捕捉到实体指称项和实体之间的语义信息和句法特征,从而能够更好地完成链接的任务。
此后,研究将输入送进Bert 编码器得到每个词向量的编码,再取其中第一位的输出送入一个线性层,最终得到一个标量、即候选实体与实体指称项的相关性分数,具体计算见公式(4):
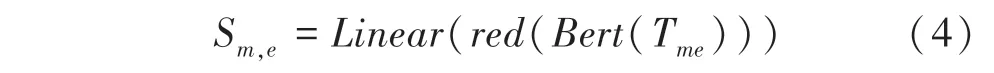
其中,T是实体指称项与实体拼接后的输入;(·)是将输入进行编码的编码器;(·)是只保留第一位编码的函数;(·)是将一维向量转变为标量的线性层。
为了通盘考虑全部的候选实体,将全部候选实体的相关性分数输入到一个层,并取得分最高的候选实体作为实体指称项应该链接的实体。计算公式如下所示:
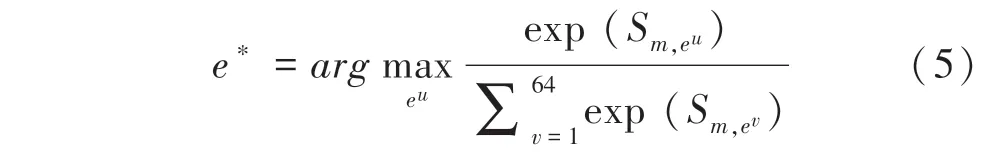
其中,e表示第个候选实体。
2.4 训练
ColBert-EL 模型的训练过程如下:模型的输入是三元组,e,,这里是实体指称项及其上下文,e是实体指称项的正例实体,是实体指称项的负例实体。正例实体是由数据集给定的,而负例实体是通过TF-IDF 技术计算得到的,是和正确实体的摘要最相似的7 个实体摘要。ColBert-EL 模型是一个二分类任务,模型参数是通过二元交叉熵损失函数来进行优化的。
MRC 模型的训练过程如下:构建了2 种不同的训练集来训练MRC 模型。第一种是通过用ColBert-EL模型生成的候选实体来训练MRC,第二种是通过用TF-IDF 技术生成的候选实体来训练MRC。在对MRC 进行训练时,如果数据中实体指称项的正确实体不包含于候选实体集合中,则将丢弃这条数据。由于利用TF-IDF 技术生成的候选实体集合中实体指称项的候选实体个数并不总是相同的,就可将候选实体个数相同的实体指称项数据放到一个批次中,用于对MRC 模型的训练。本文构建模型的参数是通过交叉熵损失函数来优化的,其中负例是候选实体集合中的所有非正例实体。
2.5 检索优化
ColBert-EL 模型采用后期交互的方式,对每个可能的实体进行详尽的评估是极其消耗计算资源的。由于文中只关注其中分数较高的部分实体,为了加快检索效率,先通过一个粗粒度的匹配算法快速从整个实体集合的离线索引中找到Top个相似实体,再使用ColBert-EL 算法对这些实体进行相似度计算。
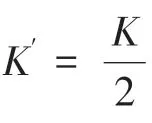
3 实验
3.1 实验准备
本文实验中使用的数据集是ZESHEL,这是由文献[6]在提出零样本实体链接任务时从维基百科文档中创建的。数据集一共划分了16 个领域,每个领域内的实体数量范围从10 k 到100 k 不等。训练集、验证集、测试集分别拥有8、4、4 个不同的领域,包含的实体指称项个数分别是49 k、10 k、10 k。研究中选用Bert-base作为ColBert-EL 模型和MRC模型的基础编码器,选用AdamW作为优化器。
3.2 对比方法
本文的方法主要是评估零样本实体链接系统的链接性能。研究时分别评估了两阶段模型的表现并与目前最优的方案做比较。在候选实体生成阶段,与文献[6]提出的BM25 模型和文献[7]提出的Biencoder 模型进行比较;在候选实体排序阶段,又与文献[7]中的Cross-encoder 模型进行了比较。
3.3 评估指标
模型预测的结果最终会被归为以下4 类:为将正类预测为正类数;为将负类预测为负类数;为将负类预测为正类数;为将正类预测为负类数。
对候选实体生成模型评估的指标为召回率(),该值可由如下计算公式求得:
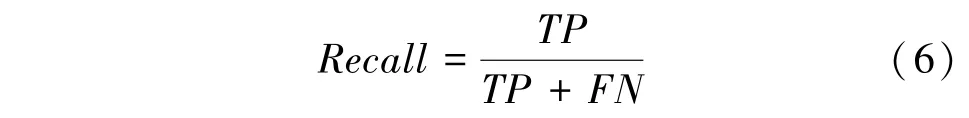
对候选实体排序模型评估的指标为和。的计算公式可写为:
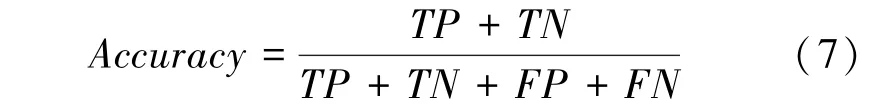
是对候选实体集合中包含正确实体的测试集中的样例在实体链接系统上的表现,即评估时不考虑那些候选实体集合中不包含正确实体的测试集实体指称项数据。而是指实体链接系统在所有测试集上的表现。
3.4 候选实体生成实验评估
ColBert-EL 模型在训练集上训练之后,挑选在验证集上表现最好的模型用来对测试集数据进行测试。在候选实体的选取中,基线选择将实体输入的位编码与实体指称项输入的位编码做点积以获取两者之间的相似度。与之相比,研究中充分利用了实体指称项和实体输入的每一位词向量的编码表示,计算了每一个可能的实体与实体指称项之间的相关性。同时,复现了基线的模型,并得到了基线模型在测试集4 个领域的表现。实验证明,本文提出的模型精度优于基线,测试集总体表现详见表1,各个领域表现详见表2。
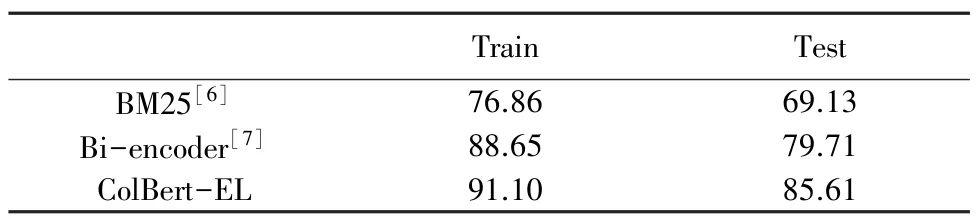
表1 训练集/测试集前64 位召回率Tab.1 Recall@64 on train/test set %

表2 测试集各领域前64 位的召回率Tab.2 Recall@64 on each domain within test set %
3.5 候选实体排序实验评估
在用ColBert-EL 模型为每个实体指称项评估完前个实体、并得到64 个候选实体后,就在这些候选实体上训练了MRC 模型,且在测试集上对MRC 模型进行了测试,结果见表3。由表3 可知,本文研究在端到端的精度上超越了基线的精度。

表3 MRC 模型非标准化精度Tab.3 The Unnormalized Accuracy of MRC model
为了进一步验证MRC 模型的有效性,研究又在文献[7]提供的候选实体集上对MRC 进行了训练。由于在用TF-IDF 技术为实体指称项生成实体的时候,每个实体指称项的候选实体个数不总是一致的,因此本文将候选实体个数相同的数据放到同一批次中进行训练。具体的分数见表4。
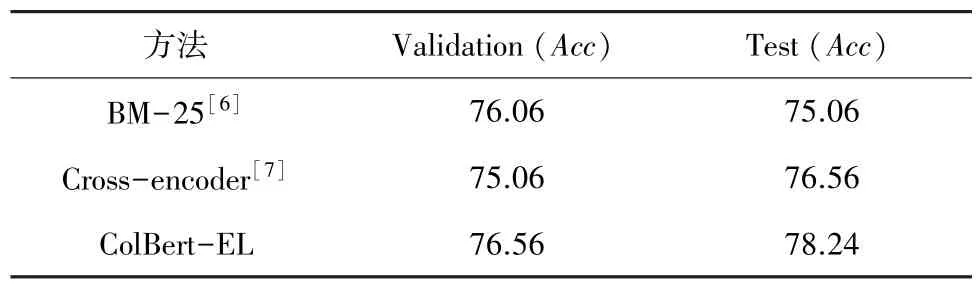
表4 MRC 模型标准化精度Tab.4 The Normalized Accuracy of MRC model
4 结束语
本文提出了一种基于ColBert-EL 和MRC 模型的零样本实体链接方法。在候选实体生成阶段,为了加快检索效率,研究中先通过一个粗粒度的匹配算法快速从整个实体集合的离线索引中找到Top个相似实体,再使用ColBert-EL 算法对这些实体进行相似度计算。在候选实体排序阶段,则考虑了全部的候选实体,将其建模成一个多项选择问题,提出了一个基于机器阅读理解的模型来对结果进行统一排序。本次研究中在零样本实体链接数据集ZESHEL 上分别对候选实体生成和候选实体排序两阶段的效果进行评估,实验结果验证了本文提出方法的有效性。

