轻量级可调分组密码算法CRAFT 的唯密文故障分析

蔡天培

（东华大学 计算机科学与技术学院，上海 201620）

0 引言

近年来随着物联网和边缘计算的飞速发展，射频识别标签、传感器、智能设备等小型物联网设备被广泛运用。由于物联网设备体积和性能的限制，相比传统设备而言，这类设备内存更小、计算速度更慢、功耗更低。这些限制使物联网设备难以在保证通信即时性的同时，还能运行安全性较高、且性能开销较大的传统密码算法，因此有必要创建新型轻量级密码算法，在设计时将设备的物理限制纳入考量，使密码算法能够在资源受限的设备中正常运行，并获得与传统密码相当的安全属性。在此背景下，轻量级密码算法甫经提出就受到了国内外学者的高度关注，相关设计与分析也已成为密码学的主流研究方向之一。

CRAFT 是由Beierle 等学者在2019 年的国际对称密码学期刊（ToSC）中提出的可调轻量级分组密码。该算法适合用于物联网中资源受限的设备，具有低功耗、高效率、高安全性的特点。由于可调参数的加入，CRAFT 在加解密的变换上更加复杂。自CRAFT 公布以来，国内外学者已经发表多种不同的密码分析方法分析其安全性，其中包括故障分析、差分分析、积分分析以及相关分析等。

故障分析作为一种主要的旁路攻击方法，与其他攻击方式相比，攻击速度上要更快、威力更强。由于物联网设备更加脆弱，攻击者较为容易地就能以故障导入的方式得到错误信息。攻击者借由错误信息推导出密码内部状态信息，如此在短时间内则可完成密码破译。

根据攻击者监听加密通信能力的不同，对密码的攻击有多种不同的假设，其中唯密文攻击对攻击者要求最低。统计故障分析是一种基于唯密文攻击的攻击方式，攻击者能够仅使用随机密文破译密钥。唯密文攻击与其它假设相比，更接近物联网的应用环境。研究表明，多种轻量级密码算法，例如LED、PRESENT 等均不能抵御统计故障分析。

本文提出了新型覆写故障模型，并设计了能够与覆写故障模型相适应的多种新型区分器，包括决定系数、雅卡尔相似系数、泊松偏差、余弦相似指数等。在统计故障攻击中，上述的故障模型和新型区分器可以使故障注入的轮数更深、所使用的故障数更少、攻击时间更短、攻击效果更好。不同情况下破译CRAFT 所需的故障数见表1。由表1 可知，利用新故障模型和区分器的统计故障分析能够为CRAFT 密码算法抵御该类型的攻击提供了重要参考。

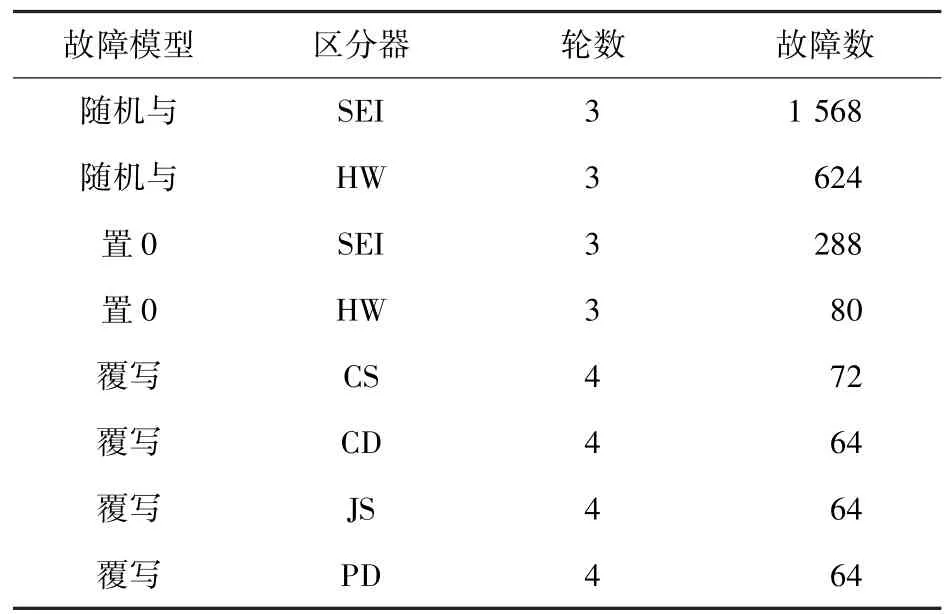
表1 不同情况下破译CRAFT 所需的故障数Tab.1 Fault numbers required to break CRAFT

1 CRAFT 算法

轻量级可调分组密码CRAFT 具有代换置换网络结构。分组长度、密钥和可调参数分别为64 比特、128 比特和64 比特。算法包含加密过程、解密过程和密钥编排算法，其中解密为加密的逆运算。加密算法共有32 轮运算，每一轮包含列混合、常数加、可调密钥加、P 置换和S 盒。特别地，最后一轮仅包含列混合、常数加和可调密钥加。加密算法和加密密钥编排算法的代码设计详见如下。

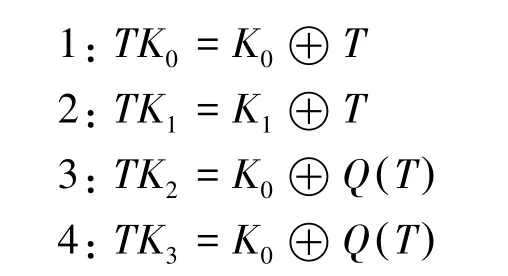
自CRAFT 提出以来，国际对其安全性进行了深入分析与研究。2019 年，Beierle 等学者在提出该密码算法时分析认为CRAFT 在相关可调参数模型中具有124 比特的安全性。同年，ElSheikh 等学者利用16 个相关密钥，对CRAFT 采用全轮差分分析的方式分析密钥。2020 年，Guo 等学者使用明文的差分和一对相关的可调参数和密钥，对CRAFT 做出15 轮分析。同年，Hadipour 等学者采用相关可调参数零相关分析的方法，利用可调参数作为输入参数的特性，通过分析零相关性的线性堆的方法实现了CRAFT 在14 轮下的分析。2021年，Hadipour 等学者通过分析CRAFT 的故障传播路径，发现CRAFT 的加密算法存在飞去来器效应，并从随机组合中区分出经过CRAFT 算法6～8轮加密的密文。

2 对CRAFT 的唯密文故障分析

2.1 基本假设

本文采用唯密文攻击的基本假设，即攻击者拥有监听加密通信的能力，但过程中仅可以获取密文。上述内容是攻击者能力最弱的假设，在实际攻击中具有强大的威胁性。攻击者可以在密码设备的运算过程中向某一轮加密过程注入故障，从而导致算法在运行中有了发生错误的能力，但攻击者并不能确定发生故障的位置的原始值和故障后的值。

2.2 故障模型

在传统的故障分析中，攻击者主要利用改变中间状态值的手段来导入故障，进而使得算法设备输出错误密文。传统的统计故障攻击方法的攻击位置一般集中在中间状态存储中，攻击面较小，且攻击目标单一。密码设计人员较容易实施物理上的防御措施。

指令跳过是指干扰处理器运行指令，使程序指令中的一部分出现被跳过的故障。指令跳过通过电磁场或激光射线触发。2010 年Trichina 等学者在Cortex M3 微处理器上实现破译系统，通过1～2 次的指令跳过，迫使CRT-RSA 算法在运行过程中出现故障，执行错误的流程，并利用错误输出破译密码。

本文基于指令跳过故障模型对分组密码的特定指令中所造成的影响，提出覆写故障模型，该故障模型使用指令跳过故障以达到数值覆写的故障效果。从而导致密码算法的中间状态发生异常，最终将输出错误密文。在对CRAFT 的攻击中，该故障模型的目标指令位于P 置换层，攻击的示意如图1 所示。在图1 中，中间状态0 号位、15 号位的值经过P 置换变换、即将写回原存储空间时，由于指令跳过故障使得0 号位的值因为未能成功更新而被15 号位的值覆写。在该故障模型中，未更新的0 号位半字节称为故障半字节，值相同而成功更新的15 号位半字节称为源半字节。

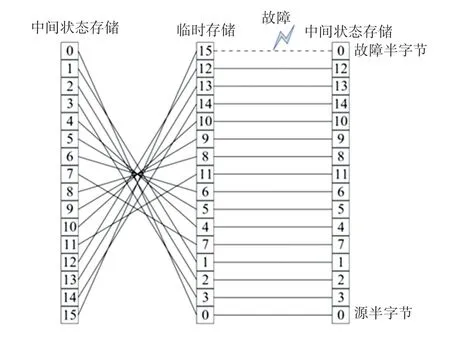
图1 CRAFT 算法的对PN 层覆写故障模型Fig.1 Overwritten faults model on PN layer of CRAFT

2.3 主要过程

在本节中，通过将覆写故障模型应用于CRAFT，并采用唯密文故障分析的方式，结合使用6个不同的区分器来分析所得的中间状态。首先，攻击者需要在某一轮加密过程中导入故障并取得相应的错误密文。由于密文受到半字节覆写故障模型的影响，根据故障模型的特征，在故障发生的时刻会有2 个半字节拥有相同的值。经过故障传播，最终得到的错误密文将会是不均匀的。故障传播示意图如图2 所示。

图2 CRAFT 算法的故障传播路径Fig.2 Faults propagation path of CRAFT

随后，将错误密文与候选密钥代入区分器进行运算，利用故障的偏差，不同的密文与密钥结合会产生不同的区分器值。根据区分器的特性，攻击者可以选取一组候选密钥，使得这组密钥对应的区分器值最大或者最小，该组候选密钥就是恢复出来的可调子密钥的值。攻击者不断重复上述过程，直到所有的可调子密钥均被恢复。每一次恢复可调子密钥的步骤如下。

攻击者在第28 轮的PN 层注入故障。所有的错误密文由不同的随机明文使用相同的主密钥和可调参数加密得出。根据CRAFT 的密钥编排算法，这也意味着加密时使用的可调子密钥相同。

本步骤的目标是恢复最后3 轮使用的可调子密钥、和，其中包含了对CRAFT故障传播的利用和区分器的使用。由图1 可知，在PN 层导入故障后，可以利用公式倒推得出故障注入时的中间状态。通过区分器对目标半字节的统计学分析并结合目标半字节的概率值列表，攻击者可以使用不同的可调子密钥计算出不同的区分器值。随后，攻击者通过选定区分器值的最大值或最小值，最终确定本次恢复的可调子密钥。倒推公式如下：

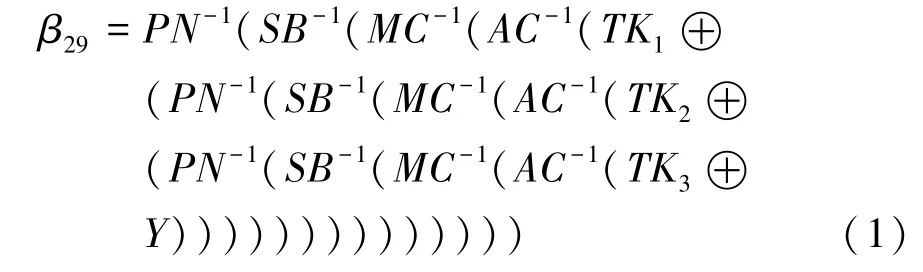
在恢复可调子密钥后，本步骤尝试恢复主密钥。当可调参数作为公共输入时，攻击者可使用可调子密钥、可调参数和盒恢复完整的128比特主密钥。当可调参数不公开时，攻击者不能恢复完整的主密钥，但可以将主密钥的数量限定在16个。将与异或，攻击者可以通过如下公式计算出：

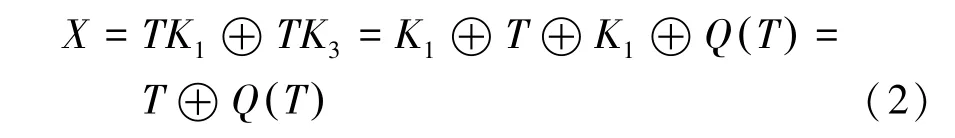
根据CRAFT 的密钥编排方案，（）是可调参数的一个排列，因此中的每一个半字节符合如下公式：

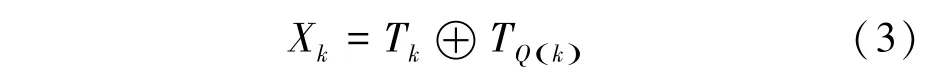
其中，∈［0，15］。

攻击者知道的值，且一旦得知可调参数中任意一个半字节值，通过图3 给出的值与值之间的异或关系图，可调参数的所有值都可计算得出。在最糟糕的情况下，即使不知道可调参数的值，亦可以通过其他进一步的分析，从16 个现有的候选主密钥中选出正确的主密钥。

图3 Tk中的异或关系图Fig.3 XOR relations among Tk

2.4 区分器

2.4.1 已有区分器

平方欧式距离（）将恢复出来的值序列与理论平均值映射到高维欧几里德空间中的2 点，并计算这2 点的距离。该区分器可以评估恢复出来的分布到平均分布的距离。Fuhr 等学者首先将区分器应用到对AES 的字节随机故障模型的分析中。该指数的计算方式如下：

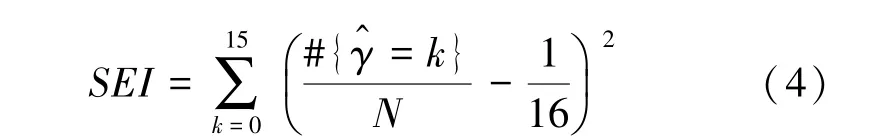
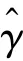
汉明重量（HW）定义为一个二进制比特串与零串之间不同比特的数量。Fuhr 等学者将汉明重量应用在对AES 的分析中。在CRAFT 中，正确的密钥将使得汉明重量区分器值最小。汉明重量区分器值可通过如下方式进行计算：

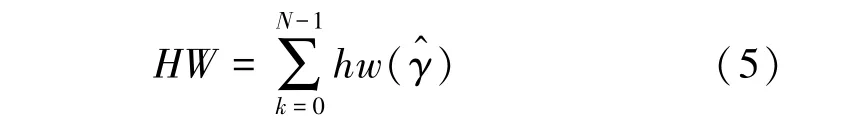
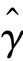
2.4.2 提出的区分器

（1）余弦相似指数（）。通过计算2 个非零向量夹角的余弦值来测量2 个向量相似程度的指数。攻击者可以通过构造2 个向量，分别包含所有源半字节和故障半字节。由于正确的密钥可以使源半字节和故障半字节的值相同，2 个向量的重合程度最大，余弦相似指数值达到最大。该指数可通过如下公式计算求出：

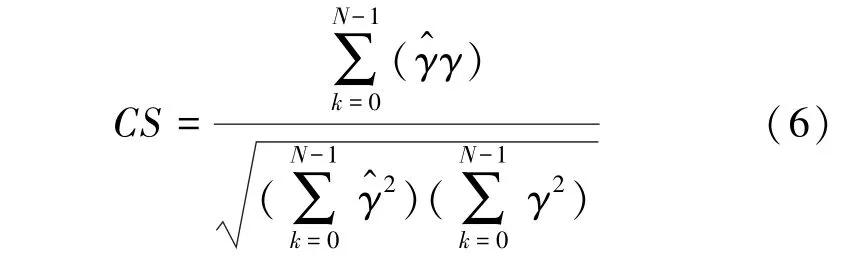
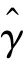
（2）决定系数（）。用于统计线性回归模型中观察值与期望值的差异，描述了数据与观察之间的符合程度。决定系数区分器在覆写模型中观测源半字节与目标半字节的差异。当候选密钥为正确密钥时，源半字节与目标半字节的差异最小，此时区分器值最小。该区分器值的计算公式具体如下：

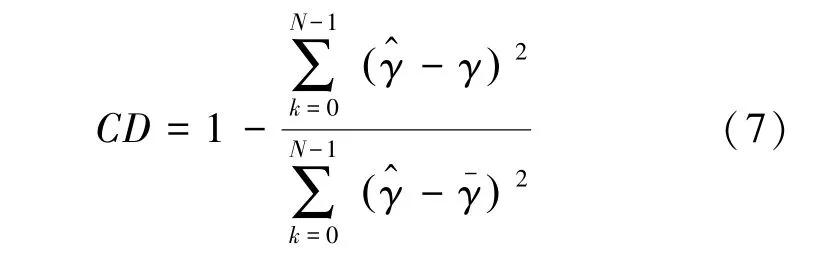
（3）雅卡尔相似系数（）。通过计算2 个集合的交集占这2 个集合的并集的比例，测量2 个集合的相似程度。在二进制中，雅卡尔相似系数可以测量2 个比特串的相似程度。在覆写模型中，雅卡尔相似系数区分器通过计算源半字节与故障半字节的重叠程度区分正确密钥。正确密钥可以使被恢复的源半字节与故障半字节相同，其雅卡尔相似系数区分器值将最大。雅卡尔相似系数区分器值的计算方式如下：

（4）泊松偏差（）。用于比较2 个广义泊松回归模型的相似度。该偏差值描述了模型与数据的符合程度。在覆写模型的条件下，该区分器描述了源半字节与故障半字节的符合程度。正确的密钥可以使得源半字节与故障半字节的符合程度最高。泊松偏差区分器值的计算方式如下：

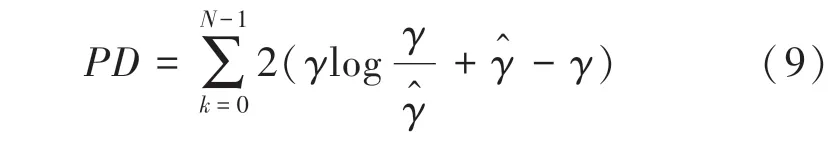
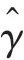
3 实验

本实验利用计算机软件模拟随机故障导入，在PC 机上使用Python 语言编程进行分析，并且对每种故障模型区分器组合运行1000 次实验。本节以恢复密钥为实验目标，并以故障数和成功率为指标，评测不同故障模型以及不同区分器的效果。

3.1 成功率

成功率是指不同区分器破译CRAFT 密码的概率。研究中分别统计了在2 种故障模型中，各个区分器恢复密钥时，不同故障数对应的成功率如图4所示。图4 中，横轴和纵轴分别表示故障数和破译成功率，不同颜色曲线代表不同区分器。当使用覆写故障模型时，余弦相似指数、决定系数、雅卡尔相似系数和泊松偏差区分器均可以高于99%的概率恢复主密钥，相比而言，使用随机与故障模型和平方欧式距离区分器的情况下，恢复密钥的概率仅有96%，其他故障模型也需要更多的故障数才能恢复正确的主密钥。

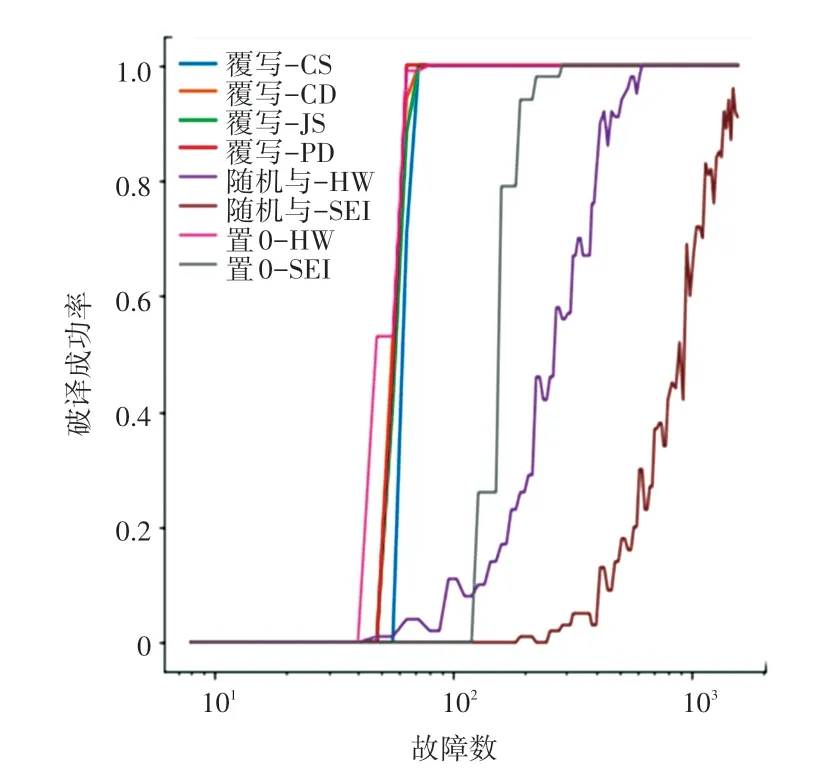
图4 不同情况下区分器恢复密钥的成功率Fig.4 Success rate of key recovery on various conditions

3.2 故障数

故障数是指不同区分器以最大概率破译密码所需最少故障数。由图4 可知，在使用覆写故障模型时，破译密码所需要的故障数大幅降低，攻击能力极强。在覆写故障模型下，余弦相似指数、决定系数、雅卡尔相似系数需要72 个故障来恢复密钥，泊松偏差则仅需64 个故障。在使用置0 故障模型时，汉明重量区分器需要80 个故障，平方欧式距离则需要288 个。在随机与故障模型下，汉明重量区分器需要624 个故障。

4 结束语

本文展示了使用唯密文故障分析的分析方式，结合6 个去分析和面向半字节的覆写故障模型，来分析CRAFT 密码系统。在最优情况下，本分析方式能够使用最少64 个故障破译CRAFT。该结果展示出唯密文故障分析是在物联网领域对CRAFT 的一个巨大威胁，为密码设计人员提供了CRAFT 密码安全性检测的方法，也对轻量级可调分组密码实现安全研究有着不可低估的参考价值。