融合迁移学习和神经网络的潜在因子模型

吴 静，宋 燕

（1 上海理工大学 理学院，上海 200093；2 上海理工大学 光电信息与计算机工程学院，上海 200093）

0 引言

随着信息时代的迅猛发展，数据呈现爆炸式增长且常以高维矩阵的形式被存储。然而，由于天然限制、技术不足等原因使得高维稀疏矩阵普遍存在。并且当面临这样的大规模数据缺失的场景时，传统潜在因子（Latent Factor，LF）模型的性能往往不尽如人意。

实际上，现实应用中总是可以使用多种评分模式来描述两两实体之间的关系，并且不同评分模式之间存在一定的关联性，即实体之间的关系并不会因为评分模式的改变而改变。也就是说，当某位用户需要对商品进行评价时，如果该用户在二分制评分模式下点击了喜欢按钮，那么在五分制评分模式中有很大概率会给出3～5 分这样的高分。因此，基于不同评分模式之间的关联性，可以通过迁移学习将辅助领域中的潜在信息迁移到目标领域，以此缓解其中的数据稀疏问题。

此外，时间效率逐渐成为评判模型性能好坏的原因之一。现有的学习方法、如随机梯度下降法等等，往往需要多次迭代达到模型收敛，从而造成模型训练效率低。

综上，本文提出的TN-NNLF 模型主要贡献如下：

（1）基于传统的LF 模型，建立了一种新的融合迁移学习和神经网络的潜在因子模型。

（2）基于不同评分模式之间的关联性，通过迁移学习来迁移不同评分模式之间的共享潜在信息，以便充分挖掘已知信息之间的关系。

（3）利用神经网络进行模型参数训练，减缓由于额外的评分领域的引入所造成的模型训练负担。

（4）在2 个真实工业应用数据集上的实验结果表明，本文提出的TL-NNLF 模型能够在保证满意的预测精度的前提下大大加快了模型训练速度。

1 相关工作

1.1 迁移学习

与经典的机器学习方法不同的是，迁移学习主要基于不同领域之间所存在的潜在联系，能够通过从相关的辅助领域中迁移共享的知识，以此来改进模型在目标领域中的学习效果。

具体地，基于迁移内容的不同，可以将迁移学习分为以下3 种类型：

（1）基于实例的迁移，即从辅助领域中挑选出有助于目标领域学习的实例。

（2）基于特征的迁移学习，即提取并迁移辅助领域和目标领域之间所共享的特征表示。

（3）基于模型的迁移学习，又称为基于共享参数的迁移，通过找到辅助领域与目标领域的空间模型的共享参数以达到迁移的目的。

1.2 自编码神经网络

一个简单的自编码神经网络模型主要包含3 层结构：输入层、隐藏层、输出层。主要工作原理是：在隐藏层将输入数据映射到维度更低的特征空间中以提取重要潜在信息，再对特征空间中所包含的信息进行重构并作为输出层数据。

一般情况下，通常使输入层和输出层样本数据维度相同，从而可以更好地重构原始数据。这里假设输入层包含个样本，，…，x，编码层包含个神经元，对应的输出层数据为，，…，y。研究中可利用欧式距离建立重构误差损失函数，得到具体形式如下：

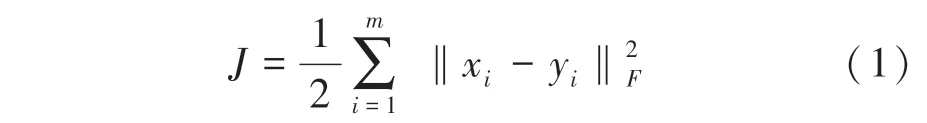
其中，表示输入层样本个数。

2 模型研究设计

2.1 TL-NNLF 模型

本文提出的模型考虑的场景是：基于五分制和二分制这2 种不同的评分模式来描述相同项目集合中两两实体之间的关系。并且将五分制评分模式领域作为目标领域，二分制评分模式领域作为辅助领域。

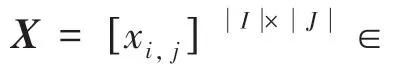
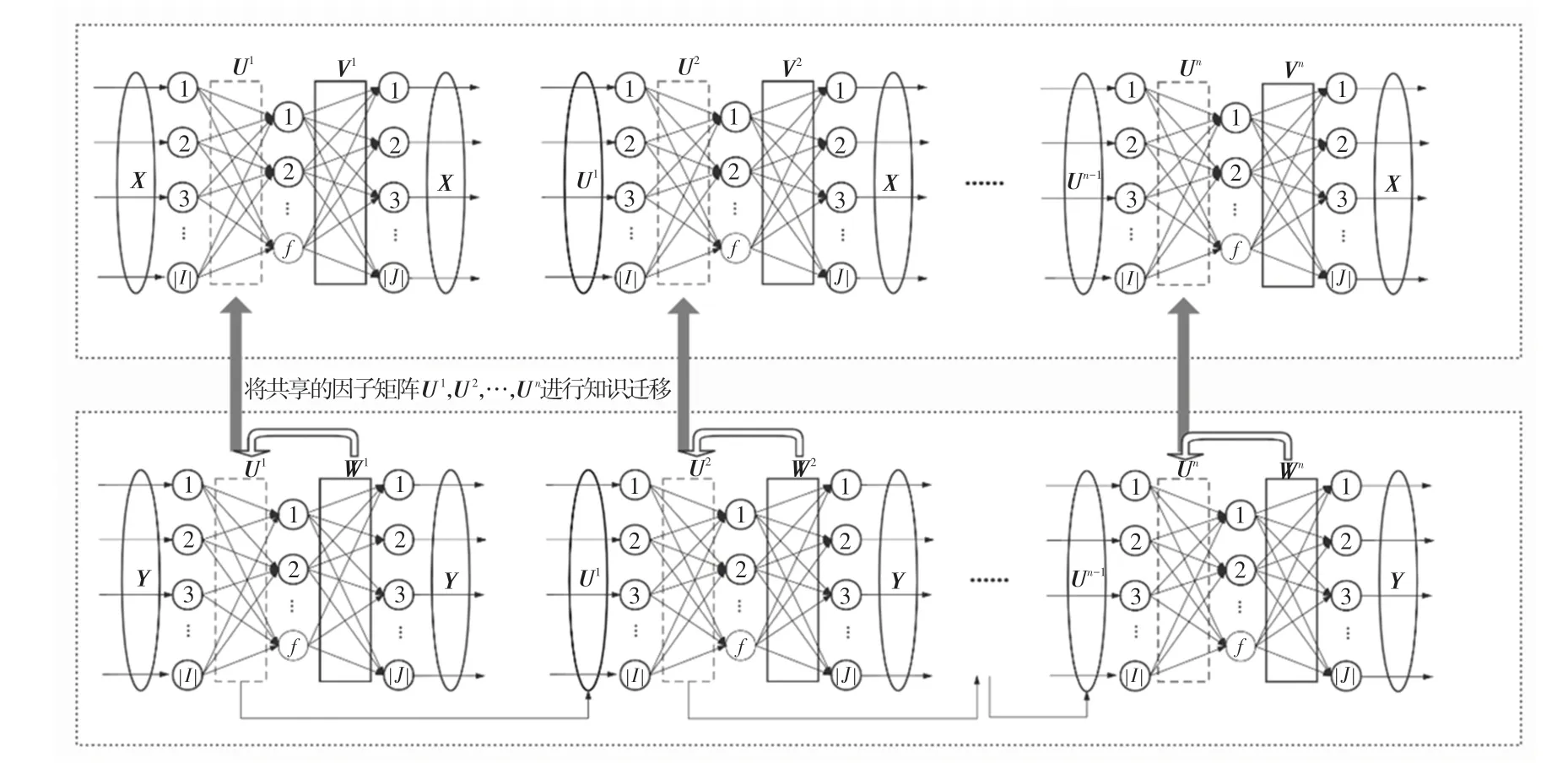
图1 TL-NNLF 模型结构图Fig.1 Structure of an TL-NNLF model

首先进行目标函数的构造，为了避免模型训练过程中出现过拟合的情况而引入正则化项，得到具体形式为：

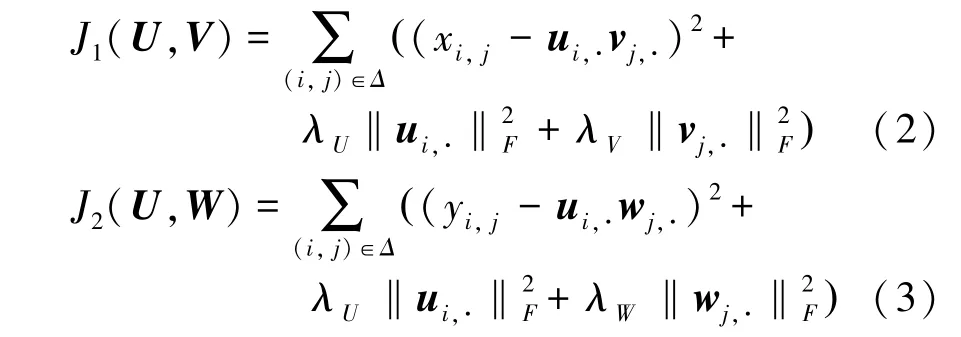
其中，x，y分别表示目标矩阵，辅助矩阵中的元素；u表示共享因子矩阵的第行元素；v，w分别表示第层神经网络中因子矩阵，的第行元素； λ，λ，λ分别表示正则化系数。

2.2 基于神经网络进行参数训练

根据图1，若假设TL-NNLF 模型中包含层神经网络结构，则可得到模型训练过程如下：

（1）当1、即模型为单层神经网络结构时。首先训练辅助矩阵，将矩阵的每一行作为输入数据，并依次训练因子矩阵和。其次将因子矩阵迁移到目标矩阵的训练过程中，此时将矩阵的每一行作为输入数据，并训练因子矩阵。

（2）当≥2、即模型包含多层神经网络结构时。其第一层训练过程和单层神经网络模型类似；而从第二层开始，则是将上一层训练好的因子矩阵U作为下一层的输入，这也有利于潜在信息的进一步提取。最后依次训练因子矩阵U，W。

接下来，基于梯度法来求解对应的因子矩阵U，V，W。若仅仅考虑单层神经网络结构、即当1 时的情况，研究可得到的具体求解步骤分述如下。

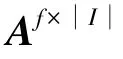
通常情况下需要使用反向传播算法训练权重矩阵和偏置向量，然而该算法容易加重模型训练负担。所以为了加快模型训练速度，本文使用随机学习算法来确定权重矩阵以及偏置向量。

（2）第二步，求解因子矩阵。根据初始化后的因子矩阵，并利用梯度法求解目标函数。研究中首先求偏导，可以得到：

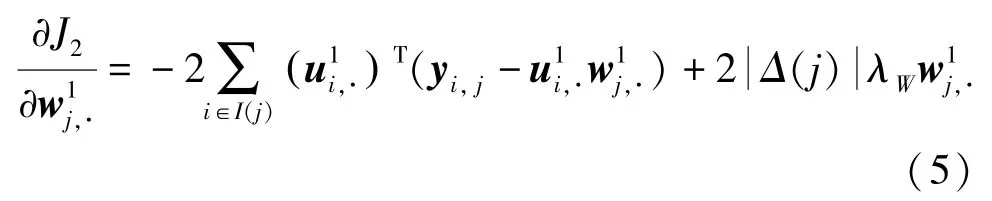
其中，（）表示矩阵每行的已知元素集合，（）表示辅助矩阵中第列的已知值集合中的元素个数。

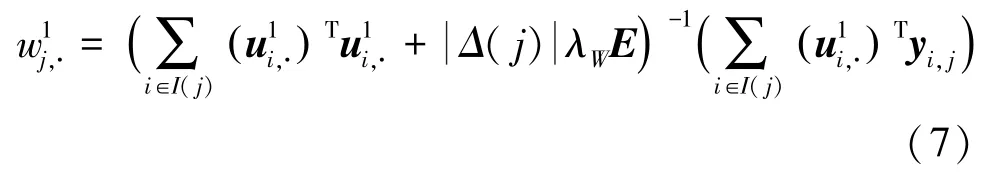
（3）第三步，更新因子矩阵。为了使其更好地近似辅助矩阵，需要进一步更新因子矩阵。

类似地，利用梯度法，首先求偏导得到：

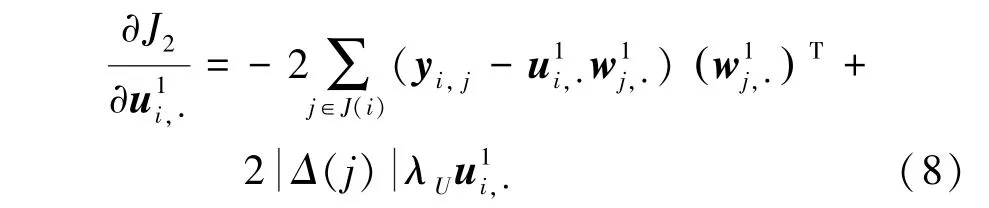
其中，() 表示矩阵每一列的已知元素集合。

（4）第四步，求解因子矩阵。此时将目标矩阵作为输入，并借助更新后的因子矩阵进行参数训练。类似地，可以得到因子矩阵的具体参数更新形式如下：

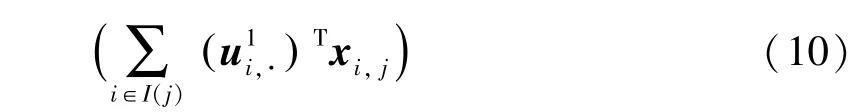
通过上述求解过程，可以得到当1 时的单层TL-NNLF 模型中各个因子矩阵中元素的具体训练规则。

其次考虑一般情况，也就是当≥2、即模型包含多层网络结构时的情况。从图1 可以看出，和第一层神经网络模型不同的是，此时将上一层的因子矩阵、即U中的元素作为下一层输入。也就是说，此时仅仅考虑潜在因子矩阵的信息提取。并且由于潜在因子的矩阵规模远远小于原始矩阵，这不仅减轻了模型负担，同时也有助于进一步挖掘原始矩阵中所包含的潜在信息。

因此，当≥2 时，首先通过随机学习算法初始化权重矩阵和偏置向量对上一步训练完成的因子矩阵U进行编码，并得到因子矩阵U的具体更新规则如下：

其次，类似地，根据梯度法，得到因子矩阵W的更新公式：

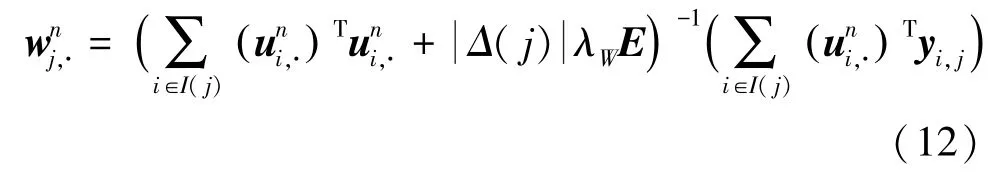
并根据求解后的因子矩阵W，进一步更新因子矩阵U，得到如下更新公式：

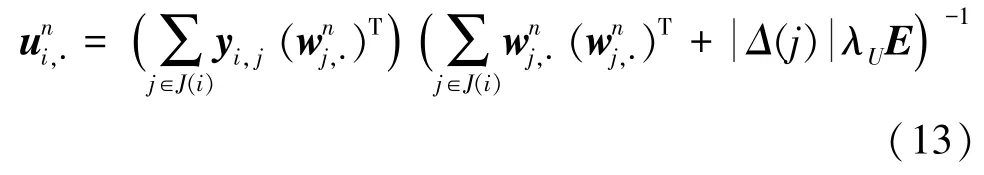
最后，则通过将对应神经网络层训练好的因子矩阵U进行知识迁移，得到因子矩阵V的具体更新公式如下：

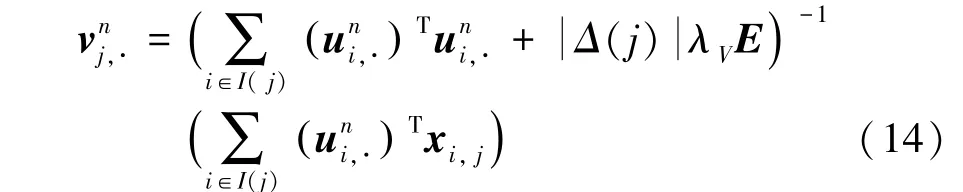
2.3 算法设计和复杂度分析

基于以上参数更新规则，研发设计了TL-NNLF模型算法，算法的步骤流程可见如下。

1.3 评定标准 分别于治疗前及治疗4周后，采用Lysholm膝关节评分量表[5]对患者疗效进行评定， 评定内容包括跛行(5分)、下蹲(5分)、 需要支持(5分)、 肿胀(10分)、 交锁(15分)、 上下楼梯(10分)、 不稳定(25分)、 疼痛25分)，满分为100分。采用视觉模拟评分(Visual Analogue Scale，VAS)来评定患者膝关节疼痛[6]：分值范围为0～10分，0分表示无痛，10分表示想象中的最剧烈疼痛。

不难发现，该算法主要时间开销来自于元素更新公式（12）～（14）中逆矩阵的计算。具体地，对于每个逆矩阵的求解需要花费的时间复杂度为（），其中表示因子空间的维度。也就是说，时间复杂度往往和呈线性关系，值越小、时间开销越少。另外，神经网络层数的设置也十分重要，这是因为越大、表示层数越多，模型训练所需花费的时间也越多。

3 实验结果与分析

3.1 评估指标

为了有效衡量提出的模型算法的精确度，采用均方根误差（）和平均绝对误差（）作为实验评估指标，具体公式如下：

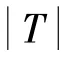
3.2 实验数据集及预处理

本文选取了2 个真实工业应用数据集作为实验数据集来验证提出模型的性能。对此数据集拟做阐释分述如下。

（1）（MovieLens 1 M）：该数据集由GroupLens 研究组根据MovieLens 网站收集的电影评分数据，其中共包含6040 位用户对3883 部电影的评分数据，且评分区间为［1，5］。该数据集密度为4.26%。

（2）（Douban）：该数据集来自中国最大的在线图书、电影和音乐供应商-豆瓣。其中包含了129490位用户对58541 个项目的评分，评分区间为［1，5］。该数据集密度仅为0.22%。

考虑到目前没有适合本文这种场景、即用二分制和五分制两种不同的评分模式来描述相同项目集合中两两实体之间的关系，因此在实验过程中参考文献［5-7，21］中的方法处理实验相关数据集。具体地，对数据集，将目前大规模稀疏的五分制评分矩阵作为目标矩阵，并通过公式（17）得到对应的辅助矩阵：

3.3 模型参数设置

在进行对比实验之前，需要事先通过参数灵敏度实验。首先将正则化系数λ，λ，λ预设为λ＝λ＝λ＝λ以降低训练成本。因此，可以明确实验中需要训练的参数包括：正则化系数、潜在因子维度、神经网络层数。具体的参数训练结构如图2～图5 所示。

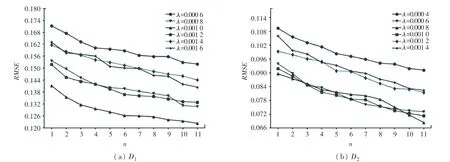
图2 正则化系数λ 对RMSE 的影响Fig.2 Influence of regularization coefficient λ on RMSE

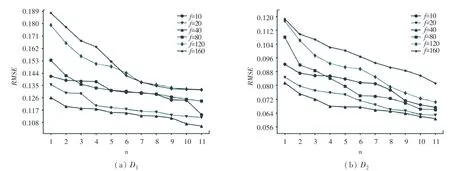
图3 潜在因子维数f 对RMSE 的影响Fig.3 Influence of Latent Factor dimension f on RMSE

图4 不同潜在因子维数f 的时间花费Fig.4 Time costs with different Latent Factor dimension f

图5 不同神经网络层数n 的时间花费Fig.5 Time costs with different layers of neural networks

图2 展示了当潜在因子维数40 时，不同神经网络层数下正则化系数对模型的影响。可以发现，正则化参数的最优值随数据集的变化而变化，并且正则化参数的最优值还会受到神经网络层数的影响。具体地从图2（a）中可以发现，在数据集中，当正则化参数的值为0.001，此时若神经网络层数1 时有最小值为0.1412，而当5 和11 时，最小值分别为0.1280和0.1223。

图3 展示了当正则化系数＝0001 时，不同神经网络层数下潜在因子维数对模型的影响。类似地可以发现，潜在因子维数会随着神经网络层数的变化而变化。具体地从图3（a）中可以发现，在数据集中，若潜在因子维数＝40，此时当神经网络层数1 时有最小值为0.1262，而当5 和11 时，最小值则分别为0.1253 和0.1054。

另外，由于时间效率也是判断模型性能好坏的关键因素，因此还记录了不同潜在因子维数和神经网络层数下的时间花销，具体结果如图4、图5所示。

从图4（a）、图4（b）中发现，在数据集上，当潜在因子维数10 时、模型训练时间仅为1634 min，而当160 时、模型训练过程则需要花费37250 min。尽管潜在因子维数越大，模型的特征表示能力越强，但同时也大大增加了实验负担。类似地，从图5（a）、图5（b）中可以发现，无论是在数据集、还是中，模型训练时间都会随着神经网络层数的增加而增加。

综上所述，本次研究中设置TL-NNLF 模型中参数为：在中，正则化系数0001，潜在因子维数40，神经网络层数5；在中，正则化系数00008，潜在因子维度40，神经网络层数5。

3.4 实验结果分析

最后为了评估本文所提出模型的有效性，共选择了3 种经典的LF 模型与本文提出模型进行对比实验，具体如下：

（1）：NLF。NLF 是一种目前应用较广泛的基于单一目标领域的非负LF 模型。

（2）：CMF。CMF 是一种跨领域的联合矩阵分解。

（3）：MLF。MLF 是一种基于随机算法的LF 模型。

（4）：TL-NNLF。TL-NNLF 是本文提出的一种新颖的LF 模型。

接着根据上述参数设置对模型进行对比实验，最终结果见表1。表1 中，每个括号中的值表示该模型在某一指标下的排序值。这里，仅考虑了本文提出模型在目标领域中的预测误差和训练时间，值得注意的是，该模型同样适用于辅助领域。

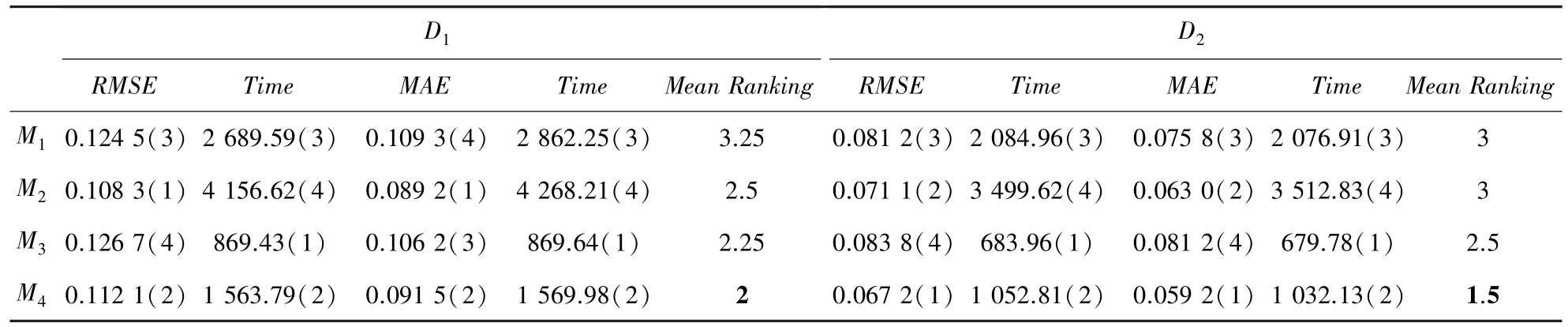
表1 模型M1～M4 在D1～D2 的最小预测误差和相应时间开销Tab.1 Lowest prediction error and the corresponding time costs achieved by models M1～M4 on D1～D2

研究中遵循的具体排序规则如下：首先将4 个模型基于评价指标和花费时间值的大小分别进行排序，其中1 表示最好，4 表示最差；其次分别计算每个模型的平均排名，例如在数据集中，模型的每项排名分别为：3、3、4、3，所以模型的整体平均排名为（3＋3＋4＋3）/4＝3.25。此处的平均排名值越低，表示模型整体性能越好。

至此，由表1 中可以得到以下结论：

（1）模型在2 个真实数据集上关于评价指标和的整体表现明显优于模型和。具体地，在数据集中，模型和分别取得最小值为01245 和01267，而引入了迁移学习的所取得的最小值为01121，较和相比分别提升了124，126。类似地，基于评价指标，模型的表现也有明显提升。

（2）模型在模型训练时间上的花费远远小于模型。具体地，在数据集中，模型取得的最小值为01083，而其在训练过程中需要花费415662 min；尽管模型取得的最小值为01121，较相比降低了038，而模型训练仅花费1563.79 min。

（3）模型的整体排名都优于其他传统的LF模型。也就是说，模型能够在保证模型预测精度的前提下大大减少了模型训练时间。因此，综合考虑模型预测精度和训练花费时间这2 个方面，模型性能优于其他经典的LF 模型。

4 结束语

如何有效缓解数据稀疏问题逐渐成为一大研究热点。本文综合考虑模型预测精度和训练花费时间两个方面，一方面基于不同模式下评分数据之间的关联性，引入迁移学习将二分制评分数据的潜在知识迁移到五分制评分领域中以缓解其存在数据稀疏问题；另一方面，利用神经网络进行模型训练以加快模型训练速度，并且通过合理地设置实验参数，能够在保证较好的预测精度的前提下大大缩短了模型训练所花费的时间。最终在2 个真实数据集上的实验结果表明，本文提出的模型整体性能优于其他传统LF 模型。最后，如何进一步充分挖掘不同评分模式之间的公共知识将成为未来的重要研究方向。