可再生能源消纳责任权重制下计及源荷储互动的电力市场均衡研究
黄欣,蒋凯,郇嘉嘉,赵敏彤,刘念
(1.广东电网有限责任公司电网规划研究中心, 广东省 广州市510080;2.华北电力大学 电气与电子工程学院, 北京市 昌平区 102206)
0 引言
近年来,由于气候变暖和保障国家能源供给安全的客观需求,发展以风电和光伏为代表的可再生能源发电变得刻不容缓。考虑可再生能源(Renewable Energy,RE)天然的波动性与不确定性,电力系统需要耗费额外的成本调用源荷储各类灵活资源以促进消纳,弃风弃光问题也是不可避免。为了提高RE消纳能力,促进绿色能源转型,世界各国提出诸如可再生能源配额制、碳税等各种各样的激励政策,中国也于2019年提出了“可再生能源消纳责任权重制度”(Renewable Energy Portfolio Standard,RPS)。
截止2020年底,全国全口径发电装机容量20.2亿kW,其中太阳能发电装机2.3亿kW,风电装机2.4亿kW[1]。大量并网的RE使得国家补贴的规模和缺口越来越大,仅2020年预估补贴缺口高达3000多亿元[2],为了减轻国家财政负担,2017年国家财政部、发改委等部门联合制定了“可再生能源绿色电力证书核发及自愿认购交易制度”(以下简称绿证交易制度)。该制度根据核定发电量给RE发电厂颁发相应数量的绿色电力证书,并通过建立自愿性质的认购平台,试图借助社会资本弥补财政缺口。然而由于RE发展形势变化,绿证交易制度在实施中遇新到了困难,国家发改委等部门因此提出RPS:一是绿证交易完全基于自愿,缺乏强制约束作用,市场交易不活跃;二是绿证交易的设立本质上是政府补贴的替代品,随着风光平价上网时代的到来,绿证交易的制度背景发生了改变。当前RE发展的主要问题已经由建设成本高昂,变成了由于大量RE电力并网造成的消纳困难。
目前,由于绿证交易制度出台的较早,且与国外实施的可再生能源配额制类似,学者们对其展开了大量的研究。这些研究大致分为两个方向,其中一个方向从规则制定和经济性的角度出发,比较了绿证和其他激励政策的区别[3-4],提出机制的改进措施[5-6];另一方向从模型角度出发研究了绿证交易对电力市场运行或市场主体决策的影响[7-9]。然而,RPS与绿证交易制度在考核主体、履约方式和交易内容等方面均存在着不同之处,因此研究中国新形势(RPS)下计及电力市场中源荷储互动的用电侧投资、交易、运行策略及形成的市场均衡状态变得尤为重要。
考核主体方面,RPS明确按照省级行政区域对电力消费设定可再生能源电力消纳责任权重,包括电网在内的售电公司、参与批发市场的电力用户和有自备电厂的企业作为承担消纳责任的市场主体接受考核[10];履约方式方面,电网公司代替非市场用户采购绿电,其余主体以电力市场化交易或者自发自用RE电力满足考核要求;交易内容方面,上述考核主体超过消纳责任额外消纳的RE电量被计为超额消纳量,可作为等价履约配额在市场中自由交易。目前关于消纳责任权重的研究大致分为3个方向:一是从机制设计和实施结果入手,分析市场设计的关键要素或者宏观上的影响:例如文献[2,11]从交易品种、市场准入、交易周期、考核监督、信用等方面研究了RPS的设计准则和适用性,文献[12]分析了当前用电情况下,RPS对RE发电企业、在运电厂乃至整个行业的影响;二是从测算入手,研究关键指标的设定:例如文献[13]基于多学科协同理论,考虑地区的实际网架结构,提出了消纳责任最优权重指标测算方法;文献[14]提出RPS下的一种综合考虑新能源开发成本和系统消纳成本的新能源合理弃电率计算方法。三从模型入手,分析消纳责任权重对整个系统运行的影响:例如文献[15]提出一种非线性的双层优化消纳模型,分析了RPS对省间-省内两级市场的影响;文献[16]构建了有限理性下结合绿电厂商、火电厂商、受考核用户三方的演化博弈理论模型,模拟量不同参数条件下超额消纳量市场的变化趋势;文献[17]建立了RPS下包含RE日前市场、常规能源日前市场、实时市场的多主体优化策略模型,研究了该制度对市场均衡点的影响。
为了研究以微电网(Microgrid, MG)为代表的积极型用电主体在电力市场中的运行策略,分析实施RPS对于电力市场的影响和用户投资的影响,文章建立了RPS下电力市场中源荷储互动的双层均衡模型,如图1所示。本文将投资折算到日,为了保证计算结果合理准确,在模型中同时考虑了负荷和新能源两方面的不确定性,并采用了基于多场景模拟的不确定性方法。
在下层模型中,建立了电能量市场出清模型与超额消纳量交易模型。用电侧报量不报价,发电侧以边际成本报价,系统独立运营商(Independent System Operator, ISO)执行市场出清并计算分时节点边际电价(Locational marginal prices, LMPs)与超额消纳量价格。在每种模拟机场景下,下层出清模型需要考虑集中式RE和负荷的不确定性,计算出不同场景下的LMPs;在上层模型中,建立了MG优化投资、交易、运行模型。以MG为代表的用电侧主体可以投资储能和分布式发电资源(Distributed energy resources, DERs),并根据上层模型计算出的LMPs以及超额消纳量价格制定运行和交易策略。在每种随机场景下,上层MG优化模型需要结合对应场景下的LMPs,考虑DER出力和负荷的不确定性进行优化投资。
本文的创新点如下:
1)建立了RPS下计及源荷储互动的电力市场双层均衡模型;
2)建立了超额消纳量交易模型,分析了MG在RPS激励下的投资、交易、运行策略;
3)利用对角化算法求解IEEE 14节点算例,验证了所提模型的可行性,并据此分析了RPS的引入对包括分布式RE发电在内的市场中RE消纳量的影响。
1 模型建立
1.1 微电网优化投资、交易、运行模型
在该模型中,用MG代替位于输电网某节点上的所有电力用户。MG可以对LMPs和超额消纳量价格做出响应,通过投资储能和DERs降低运行成本。其成本函数如下:
约束条件为:
MG的超额消纳量交易收益由当日交易量收益和留存消纳量期望收益构成。这是由于:虽然期望收益不能归入当日交易的现金流,但是其体现了MG对自身成本回收和预期收益的估计,会对DERs的投资决策产生影响。
有关MG内部DERs和ESSs的运行约束如下:
其中:公式(11)(12)约束了WT和PV的发电功率不能超过最大值,,该最大值由投资数和自然资源决定;公式(13)(14)约束了ESS的充电功率和放电功率不能超过投资的最大值,。公式(15)描述了ESS储能值与充放电效率,有关,(16)描述了ESS内的荷电状态与储能值以及储能容量有关,不能超过上下限,。代表储能系统(energy storage system, ESS),风机(wind turbine,WT)或者光伏(photovoltaic, PV)的投资数量。
值得说明的是,为了综合考虑MG的DER规划与运行、交易,本文利用年金现值系数将DER全周期的建设运维成本分摊到每一年,再分摊到每日成本[19](详见算例-数据描述)。不排除有更加精确的成本描述方法,但是本文的研究重点在于可再生能源消纳责任权重制下的市场均衡,为了突出分析多个市场主体MG整个投资、交易、运行优化过程,简化了投资成本的分摊模型。
1.2 电力市场出清模型
在本文中,ISO根据上层模型中各个MG上报的净负荷需求,执行电能量市场出清程序,计算LMPs。市场出清模型目标函数如下:
约束条件为:
电能量市场中参与发电侧竞争的有RE发电机组和传统的火力发电机组。等式(18)要求满足电力供需的实时平衡,即火电机组功率与RE机组功率等于净负荷。为火电机组单位发电功率的成本,假设。公式(19)要求系统提供足够备用,这里假设系统的备用是关于净负荷和RE消纳量的线性函数,权重分别为和。公式(20)(21)为直流潮流下的线路约束,其中:为节点功率转移分布因子;为第k条线路的可以传输的最大功率值。公式(22)—(25)为机组的运行约束,火电机组所提供的电功率与备用功率在可行运行区间内运行,不能超过最大上爬坡和下爬坡约束,RE机组中标功率不能大于自然资源决定的最大发电功率。
由MG模型可知,消纳责任权重制主要是通过影响MG内的优化决策实现与电力市场的互动,而下层市场出清模型的主要作用是为上层MG提供变化的LMPs信息。是否考虑机组启停约束会改变出清模型内部的调度结果,但并不会影响消纳责任权重制与电力市场之间的互动关系。而且,从一天的时间尺度来看,机组的启停状态大概率是已知的。因此,为了突出文章重点,提高文章可读性,本模型中忽略了机组组合约束。
1.3 超额消纳量交易模型
超额消纳量交易可以被看作基于数量竞争的古诺模型[18]。根据古诺模型,市场出清的价格可以表示为:
当超额消纳量市场中供给不够时,没有完成履约要求的主体需要承受高价∑惩罚。即公式(27)所描述的价格-供给曲线在时的交易价格等于惩罚价格。上述曲线可以利用历史交易数据,利用如最小二乘法等方法拟合得到。其中系数代表着履约失败时单位消纳量的惩罚价格。
若该日风光大发,可能所有MG的公式(6)均大于零,需要出售。这时,超额消纳量价格因为大量的出售量而处在较低的水平。部分MG因为相对较高的预期价格和成本而放弃出售消纳量,使得消纳量价格有所回升;上述过程最终收敛达到均衡状态。
若所有MG单元的公式(6)均小于零,需要购买。这时,超额消纳量市场的价格因为没有卖方而达到极值,等价于所有的MG需要按照罚款价格购买消纳量。然后,由于此时消纳量价格处在较高的水平,可能会促使部分MG提高DERs的投资来提高自己的消纳量。
值得说明的是,虽然可再生能源消纳责任权重是按照年度来进行考核,但是超额消纳量可以按日交易[15,17-18]。
2 求解算法
上述双层模型形成了不同MG投资、交易、运行策略下的市场均衡问题。因为有多个消费者,所以这个问题是一个有均衡约束的均衡问题(equilibrium analysis with equilibrium constraint,EPEC)。本文采用对角化算法(diagonalization algorithm, DA)来求解EPEC[19]。只包含一个MG和ISO的双层模型形成了一个有平衡约束的数学问题(mathematical problem with equilibrium constraints, MPEC)。DA将EPEC分解为许多个MPEC,在每次迭代中固定其他MG的策略,求解每个MG独自的投资、交易、运行策略。在每次迭代中继续进行分解操作,直到MG的策略收敛,如图2所示。
3 算例
在2.90 GHz CPU和16GB RAM的计算机上,使用MATLAB 2016b和CPLEX 12.6[20]对算例进行测试。
3.1 数据描述
在本节中,对IEEE 14节点系统进行仿真,以验证所提出的模型。其中有3个火电厂和2个集中式风电厂,其所在位置如图3所示。表1列出了所有发电机的参数。

表1 发电机参数Table 1 Parameters of generators
本文的算例分析中,同时考虑了新能源和负荷的不确定性。然而,为了突出对可再生能源消纳责任权重制下市场均衡和投资结果的分析研究,仅以风电作为新能源发电的代表。因此,本算例的IEEE 14节点系统和MG的DERs投资仅有风电。为了描述负荷和风电的不确定性,使用K-means从2016年年度负荷和太阳能发电量数据[21]中生成10个典型的每日场景。
为了简化求解,系统中只有5个分别位于节点4、5、10、12、13上的微电网,期望的超额消纳量交易价格分别为200、220、240、260、280元/MW。本模型中,MG可以投资WTs和ESSs,每个WT的发电容量为45 MW,每个ESS的储能容量为10 M W·h。其余有关ESS的参数如表2所示。根据消纳责任权重的要求,假设用电主体按天履约,每天需要购买等于自身投资前日用电量的20%的RE电量。

表2 储能参数Table 2 Parameters of energy storage system
根据文献[22],WT的建设成本为1931USD/kW(约合人民币12570元/kW),为了获得年均投资成本,假设WT和ESS能使用20年,以1.25%的利润率计算年金现值系数,进而获得年均WT和ESS的年投资成本。因此,WT等年值成本约为740元/kW,换算到日值约为2元/;ESS的等年值成本约为2588元/[23],换算到日内约为7元/。根据文献[18],超额消纳量市场中的参数
3.2 MG投资、运行策略
MG依据从电力市场中获得的LMP,以及从超额消纳量市场中获得的超额消纳量交易价格,决定是否投资建设WT和ESS。表3是引入可再生能源RPS前后WG的投资情况。

表3 投资结果Table 3 Results of investment
MG在有无RPS前后的储能投资不变,但是WT的投资数量均发生了变化。最终均衡状态下的超额消纳量市场交易价格为270.4元,大于MG4、MG5、MG10、MG12的预期卖出价格,低于MG13的预期卖出价格,因此,前者在引入考核之后增加了WT的投资,MG13减少了原有的WT投资。由于超额消纳量交易市场中利益相对较大,储能的运行倾向通过快充快放增加风电的消纳量,因此ESS的储能容量需求降低,有无RPS前后ESS投资无变化。
值得明确的是,在引入RPS之后MG总的WT投资和发电量上升;在日前电力市场中,虽然MG净负荷的下降,但是由于集中式可再生能源发电厂报地板价出售电力,MG的DERs投资不影响批发市场的可再生能源发电量。因此,引入RPS之后,电力系统总的可再生能源消纳量上升。
如图4所示的是MG4在有无消纳权重责任制两种情况下的运行策略。由图4可知,引入RPS之后WT的投资量增加,极大地降低了日用电负荷最大。同时由于WT的逆调峰特性,夜间的电力需求全部由WT供应。除此之外,MG在运行优化中通过ESS实现了两个功能:一是通过频繁快速的充放电控制,在增加WT消纳量的同时平抑了WT波动对系统的影响。二是通过在低电价时间充电,高电价时间段放电(如图12点左右时刻)实现削峰填谷,赚取价格差。
3.3 MG超额消纳量交易策略
图5是MG5在有RPS下的投资运行曲线,可以发现不同MG应对RPS的策略大不相同。这主要有以下3个原因:一是MG节点位置的不同承受了不同的LMP;二是MG对于超额消纳量交易价格的预期不同;三是MG的负荷情况不相同。
表4是不同MG的交易结果。由表4可知,由于MG13的期望消纳量交易价格高于市场实际交易价格。MG13选择不建设减少WT建设,转而向市场中购买超额消纳量。
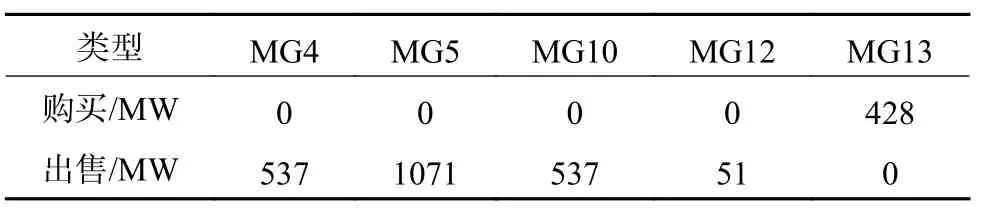
表4 消纳量交易结果Table 4 Trading results accommodated quantitiy in RPS market
4 结论
本文旨在通过研究RPS下电力市场主体的投资、运行、交易决策问题,求出均衡状态下市场主体内源荷储互动结果,从底层用户角度评价RPS对电力市场的影响。文章建立了RPS下电力市场中源荷储互动的双层均衡模型,下层模型中ISO执行电力市场出清和超额消纳量市场交易,上层模型中MG根据两个市场的交易结果优化投资、运行、交易策略。最后以IEEE 14节点系统为例,使用对角化算法迭代求解并验证了上述双层均衡问题。分析结果表明,MG投资、运行和交易策略在RPS下发生显著改变,系统可再生能源消纳量显著提升。

