基于模型无关优化策略的风电短时回归预测框架设计
丁琦,邱才明,2,杨浩森,童厚杰
(1.上海交通大学 电子信息与电气工程学院,上海市 闵行区 200240;2.华中科技大学 电子信息与通信学院,湖北省武汉市 430074)
0 引言
新能源发电设施的出力预测任务在当代高度数字化的电力系统中承担了关键的基础数据支持作用,如在调度任务中对由复杂传感器网络采样的规模级电力时空数据提供分析服务、或提供量化依据来辅助电力系统的数字化决策等,从而达到降低能源开销、提供差异化服务等目标[1]。特别是近年来融合太阳能、风能等多种新能源的综合能源系统加速入网,占有比例持续上升并且在部分地区电力系统中逐步占据关键地位。分布式多地部署使得新能源发电端设备极易受到具备时空大数据特性的温度、光照、风力等环境参数影响,导致系统发电端出力变化具有明显的实时性、间歇性,呈现显著的非线性、波动性、不确定性的统计特征,对电力系统稳定安全运行提出了挑战。特别是当前经济恢复的特殊时期,电力数据预测能够有效地为疫情防控和复工复产提供数据支持。在实际负荷预测任务中,往往需要考察基于上述情况在结合气象、气候、地理环境、节假日等因素后生成的多维负荷数据结构体,这对高度依赖相似历史数据特别是气象数据和基于物理模型的传统预测方法提出了严峻的挑战[2],显著提高了多任务预测问题的难度。
目前由于深度神经网络具有对规模数据进行自动地特征建模等能力,相比经典方法其在多任务预测上的精度指标有显著地提升,因此大量文献基于统计和数据的智能策略提出了许多有效的预测方法并广泛应用于电力负荷预测领域。但从提高神经网络对预测任务的泛化能力出发,重点分析优化和学习训练过程可注意到,多数文献的解决方案呈现典型的二阶预训练-微调分离式训练流程。该流程特点是:对已知的规模级标注数据生成预训练模型,在此基础上,重点考察改造模型架构的方法,实现将模型参数迁移至新任务数据集再训练。
如文献[3]从特征融合角度提出,基于聚类算法,首先按时间属性对工作日和周末的短期负荷数据精细分类并分别训练支持向量机预测模型,最后用细菌觅食算法融合多个模型和新类别数据,实现对短期负荷预测精度的提高;文献[4]从数据特征角度,设计二阶迁移方法融合多源域历史负荷数据将K-means聚类和门控循环单元(gate recurrent unit,GRU)融合作为一次特征提取,并考察基于时间遗忘因子进行二次特征筛选,从而利用二阶迁移方法在极限学习机(extreme learning machine,ELM)模型中融合各预测任务的源数据实现精度提升;文献[5]呈现典型的二阶迁移训练特点,首先构建工作日数据的负荷预测网络作为模板网络进行充分训练,然后根据迁移权重选择性冻结模板网络关键权值作为迁移结果后,重新初始化其他结构作为适配节假日数据的预测网络,在新数据上进行微调;文献[6]从多模型综合架构的角度出发,设计底层深度置信-顶层多任务回归预测框架的多元负荷预测系统,提出以并行的协同训练方式实现模型层面上短期电、热、气等多种负荷预测子任务的直接融合,当预测误差超越允许阈值时,接纳新类型数据再训练,实现对多任务的整体预测框架设计;文献[7]从多源数据融合角度出发,设计多分支输入模型,通过动态分支结构调节用于挖掘、提取历史负荷特征的全连接网络与提取图像数据的标准卷积网络输入,然后嵌入多分支结构的各局部输出,作为底层预测模型的联合输入,从而有效提升了多特征信息的挖掘效能,实现了对多母线多传感器任务在模型层面的融合;文献[8]从重构数据维度的角度出发,首先基于离散小波技术对非线性关系较为复杂的时序数据进行基于离散小波的高低频分解构建扩增数据,然后充分利用Spark框架的高效并行训练实现在时钟频率驱动的循环深度网络模型上高低频信号的组合训练,将各组合模型结果取加权评价作为融合的指标;文献[9]从共享权值角度,对智能能量系统(intelligent energy system,IES)电、热、冷子任务分别训练独立的长短时记忆网络(long short-term memory,LSTM)同时,对各网络剥离若干神经元,拼接成各子任务共享的局部共享LSTM网络,从而当在线训练新类型数据时,采取上述典型的硬共享方法迁移共享网络参数进行微调,实现多任务预测精度的提高。
从上述文献比较、分析、总结可见,当前文献对多任务预测的技术路线,或高度依赖于精密设计人工特征筛选,或在流程上选择多种经典模型融合技术的策略组合,或依托对已知高效网络模型施加结构性局部调整。从训练模式和优化方法切入的文献较为稀少。如文献[10]尝试性地将基本二阶优化方法引入负荷预测,通过分割数据构建多个训练模型分批次盲目训练以扩大参数空间探索较优的参数分布,但仅验证了单维度负荷数据情况下多层感知器模型的有效性;文献[11]则侧重整合损失函数,在回归预测的输出模块通过多层线性结构联合多种评价函数作为深度网络训练的综合损失函数,在训练过程中调节各指标的贡献权重。该方法可视为多分支网络融合的一种特例,对优化方法缺少进一步探究。
基于上述分析,为进一步提高预测模型对多源多任务数据集的多维隐含特征融合和参数迁移能力,本文从改进深度网络的优化方法的角度,引入模型无关元学习[12](model-agnostic meta-learning,MAML)策略,并针对性地进行修改,尝试提升模型预测的泛化性能。MAML策略及其体系属于元学习中基于优化策略的分支。元学习旨在解决如何学习的问题,相比典型深度网络学习策略,主要具备3类特征:训练过程中包含学习子系统、具备可迁移的已训练模型参数、动态调节学习偏差。
MAML策略基于二阶优化思想,起初针对呈现数据类别多、单类样本数据规模少的小样本数据学习任务,其优势在于:第一,二阶优化思想强调在模型的训练优化流程中构造双循环,外循环用于不断对随机建构的任务更新神经网络的初始参数状态,内循环将外循环训练得到的参数初始状态对新数据集施加若干快速迭代,实现利用内循环的二阶导信息迫使模型习得更优的初始化参数的思想[13],从而能够具备比一般的预训练-微调的分离策略对多任务具备更好的快速适应能力;第二,MAML策略自身是一种简洁的优化框架,以二阶优化的角度为多任务回归问题提供了一种能快速兼容多数基于随机梯度下降优化方法的深度学习模型的高效学习策略,在实践中已验证可取得和设计迁移特征或模型融合方法相媲美的性能提升[14-15],可直接利用该框架改造已有的深度网络模型。
基于上述分析,本文以多任务风机出力预测为例,进一步研究MAML策略在电力负荷预测场景的应用,提出一种基于MAML策略、面向多任务的回归预测框架。
1 基于MAML策略的短时预测框架设计
1.1 多任务回归预测问题
短时风电出力预测问题呈典型的回归特征。具体考察多任务数据集XT,Nt,kt,其中:T为任务数;Nt、kt分别为第t类任务的采样样本数和传感器输入维度;匹配的功率数据为YT,Nt,则优化目标可形式化描述为
式中:回归模型为f;其模型参数为 θ;L为损失函数。本文中L采取均方误差(mean squared error, MSE)、均方根误差(root mean squared error, RMSE)、平均绝对误差(mean absolute error, MAE)、平均绝对百分比误差(mean absolute percentage error, MAPE)作为回归模型训练质量的指标,在批训练下各指标定义可描述为
式中:N为数据的批大小。
在典型的预训练-微调的二阶方法中,多任务回归预测问题按任务类别根据实际情况拆分成预训练数据集T0和微调数据集T1,然后分别就2个数据集独立执行回归训练,即:
并对各任务s重新构建新的随机数据批次,交替执行周期t下的梯度计算:
显然在该训练策略中,虽然考察了联合调控损失计算、设计模型结构等融合策略,对数据集T0和T1仍采取了训练独立、分离优化的方法,其融合效果存在进一步提升的空间。
1.2 基于MAML策略的回归预测任务框架
1.2.1 框架介绍与MAML策略描述
框架参考MAML策略对多分类小样本数据的元学习设计,将该设计的特点迁移至多任务预测任务,尝试实现利用单回归模型融合多任务数据的泛化效果。优化目标可描述为
后者描述为:
其中 θinit为初始化参数。由公式(9)(10)可见,本文采取的MAML-微调策略与预训练-微调策略的区别是,MAML策略随机构建了对预训练数据集D的参数空间,即:
如此构建和搜索实现了对各任务体更优的参数初始化设定,从而辅助内循环微调在其他任务数据D′上训练和搜索的最优解,即
式中:t,t1分别为外、内循环周期。
1.2.2 数据集生成
为生成适于外循环搜索参数初始化分布的分割数据集,使内循环按公式(12)习得的 θ*到对各任务在独立训练下的理想参数的距离期望最小,即
式中:s为综合任务体;R为参数间的距离度量。首先根据任意预设的容积为T0的抽样任务字典,将给定的T类任务数据和功率数据按任务维度随机拆分、重组为MAML数据集和微调数据。
具体地,对拆分数据,从T0中随机抽取nway个单任务,每个单任务再随机抽取kshot个样本,称该抽样操作生成的数据结构为综合任务体。特别地,为有效应用随机梯度下降 (stochastic gradient descent,SGD) 优化器且不破坏原初数据的时序依赖性,需保持连续抽取kshot长的顺序样本。如此多次随机抽取单任务的样本片段并重构为综合任务体后,可进一步将多个综合任务构成反向传播中损失函数计算的单个数据批次。其中,称对二分集D′和D再次二分后生成的片段长kshot的数据集为支持集,剩余样本同操作构成查询集。
由此,通过随机抽取的组合方式,实现了将多任务数据按上述“部分任务-部分样本”结构的综合任务体重构为4个数据集,即SMAML、QMAML、SFinetuning、QFinetuning。具体算法可见附录算法1。
1.2.3 训练策略
区别于对训练-验证集执行反向传播、在测试集执行预测的常规训练,该框架呈现了双层循环、局部误差计算、分组更新的特点。
首先对SMAML数据集综合任务体执行推理计算,执行依SGD方式的梯度计算,获得该任务体下的模型参数 θs,但不应用θs更新该阶段模型参数。
然后进入微调阶段,应用参数 θs生成回归模型副本,对SFinetuning数据集执行推理和梯度计算获得,再应用参数对QFinetuning数据集执行验证操作。完成微调阶段后,利用和微调数据集无关的模型参数 θs对QMAML数据集执行推理计算、反向传播和梯度更新并作为本轮的最终更新结果。如此再从SMAML取下一个综合任务体重复操作,直至训练完成,以微调阶段最优模型参数 θ′为最终结果。具体的训练算法可见附录算法2。
具体地,设第s个综合任务体初始参数为,则单循环学习下,第t个训练周期参数的梯度更新根据泰勒公式可展开为
再考察双循环结构下权值梯度,若第t次外循环时,内循环完成t1;损失函数L;初始参数 θ0;内循环权值更新函数为Ut,满足:
用公式(15)及依梯度传导的链式法则有:
代入公式(14)至公式(16)并忽略极小项后,
由上述可见,该框架的核心策略是构造多个随机的综合任务体后,在双层循环中,由外循环对分割生成的时序片段批次按公式(17)前项随机搜索更优的初始化情况,由内循环按后项二阶导信息将局部优化后的参数 θs快速适应至对其他任务的回归预测任务,最终实现提升回归模型泛化能力的目标。
1.3 预测模型介绍
1.3.1 Seq2Seq预测模型和注意力机制
该模型具备天然适应时序数据张量的编码-解码结构。具体地,编码器、解码器结构的核心组成为多层长短时记忆网络[16-18],解码器以单层全连接网络输出预测数值。
注意力机制用于解决在长序列输入情况下,Seq2Seq中编码器编码的语义向量无法充分表征长序列信息、长序列信息在编码时前置信息覆盖等问题。该机制重点聚焦区分Seq2Seq模型中编码器和解码器的空间状态的相似性,并对解码器各输入状态执行软寻址操作以提高关键输入的概率占比。
其机制分为二步,首先,计算编码器隐含状态hj与编码器隐藏状态si-1的关联权重eij,即
式中:V,U为注意力机制的权值空间。
根据权重系数对编码器输入执行Softmax归一化处理获得关联系数aij
第二步,以aij作为权重对编码器首次输入的隐含状态hj或多次时序计算后的隐含状态si-1取加权和作为解码器的部分输入。
1.3.2 时序数据的窗口机制
图2以Seq2Seq模型为案例,描述了经滑窗操作的数据流在计算图中的传播情况。具体地,对序列长度为L的k个传感器阵列数据xL,k,生成总窗口长度为m、 其中包含u个后置预测数据的传感器数据窗口xm,k,并匹配生成总窗口长度为m-u的历史功率数据窗口ym-u。 传感器窗口xm,k经由编码器编码生成隐含状态h,并协同解码器上一隐含状态s经注意力模块处理后嵌入到历史功率窗口数据中作为解码器的联合输入,最终经解码计算生成预测长度为l的回归值yl参与反向传播。
特别地,为进一步强化不同窗口间沿采样维度的时序数据的时间耦合关系,减少训练过程的逐批次平均化计算误差。若滑窗的滑动步长为t′,则在扫描顺序数据片段时,取本轮窗口对应的上一窗口输出预测值的后m+l-t′个功率作为下轮采样步骤中历史功率窗口的早期输入。从而基于对历史预测输出的考察,降低了功率预测输出部分沿时序采样的累计误差,一定程度上缓解了对长时序输入功率后端数据的预测影响问题。
1.3.3 Transformer预测模型和自注意力机制
Transformer网络呈编码-解码结构,特点是以自注意力机制替代了循环网络结构[19]。该机制同样针对长序表达和网络记忆问题,动态建立了任意长度下长序列数据的长距离依赖关系,从而以点积形式实现自对齐的学习即
式中:Q、K、V为对同一输入向量经线性变化生成的二维矩阵,即Q=XW,区别于注意力机制中对计算时序的软编码;dK为用于缩放点积的方阵K维度;QKT积用于评估输入向量和模型记忆特征间标记对标记的相似度,从而评估窗口内单个负荷数据对整体采样序列的相对重要性。此外,由于该结构取缔了循环结构,可有效提高训练的并行度。
Transformer网络的编码器由多输入注意力模块和线性层构成,其中单个多输入注意力模块等效于多个自注意力模块的拼接集成。解码器额外增加了注意力机制,考察解码器输出Q和自身自注意力模块变量K,V的相似度。
1.3.4 Synthesizer预测模型
该模型进一步简化了Transformer模型的自注意力机制,可视为对后者的压缩[20]。该策略构造了参数化函数F,直接将输入变量的序列长度投影至输出变量长度。具体地,将自注意力模块公式(20)的状态变量K常数化或初始随机化,将动态自注意力计算的点积操作,应用双线性层简化至静态矩阵计算,即
即Synthesizer弱化了自对齐学习中的标记间的交互,是一种取缔了标记对标记的点积计算的简化变体,可取得和Transformer可竞争的预测性能。Transformer和Synthesizer采取与Seq2Seq相同的时序窗口生成机制,其计算图相当于图2以相应模块取缔LSTM和注意力模块。
2 算例分析
2.1 实验设定
2.1.1 数据集介绍与设定
本文采用数据集GEFCom2012。该数据集记录了7个风电场从2009年7月1日—2012年6月28日的历史功率出力测量和风力信息,其中风力信息包括纬向和经向风分量及其对应的风速和风向等4类信息,采样间隔为1h,记录形式为在每月奇数日0:00和12:00开始各独立测量48次。为便于对比,选择2010年12月31日前的数据用于训练,数据集其余部分用于预测评估。
2.1.2 实验设计与模型参数介绍
为有效对比本文提出的基于MAML的回归预测框架和预训练-微调的一般模式,将本文方法作为实验组,并设计对照组如下:将SMAML、QMAML、SFinetuning合并作为训练集、将QFinetuning作为验证集。同时为进一步验证框架有效性,预测模型包括4类:算例部分介绍的有注意力机制Seq2Seq和有自注意力机制的Transformer、Synthesizer,以及常见的卷积神经网络(convolutional neural network,CNN)-LSTM模型,其中CNN-LSTM的架构设计为将经过单层尺寸不变的卷积层和平均池化层处理后的风速信息嵌入历史功率窗口作为LSTM网络的输入,其输出展开后经全连接层变换输出预测功率。如无其他说明,实验组和对照组采用相同的参数设置,如注意力机制等,在训练过程中采取Adam优化器。特别地,为降低连续片段的预测误差积累,在训练过程中,将本次窗口的先期输入替代为上次窗口的输出后段。
实验实现基于Pytorch 1.8框架;计算平台为NVIDIA 1080 GPU,具体实验参数设置如表1所示。

表1 实验参数和模型参数设定Table 1 Setting of experiment parameters and model parameters
2.2 数据预处理及生成
数据预处理过程分为补偿和归一化操作2步。首先对7个风电场的风力输入数据和出力数据的缺失部分按插值补偿处理,其次逐维采取离差标准化预处理,将数据归一化放缩至 ± 1之间。
为进一步利用功率数据的时序依赖性和提高模型训练效率,本文利用滑动窗口沿时序顺序对原始数据扫描。其中对部分数据缺失的早期窗口或后期窗口采取延展重复末端数值的补偿方式。在利用前滑窗部分模型输出更新历史功率窗口时,直接采纳最近一次的迭代结果以简化重叠部分的处理。
2.3 结果可视化与实验分析
本文以Seq2Seq、CNN-LSTM、Transformer、Synthesizer模型为算例,重点考察各模型在MAML-微调模式和预训练-微调模式下因训练模式差异导致的精度变化。为便于可视化,在图3-6中截取部分拟合结果片段(其中蓝色曲线为归一化后输出的真实值,红色曲线为同一模型在MAML策略下的结果,绿色曲线为同一模型在预训练-微调策略的结果),其中横轴仅表征截取片段的相对时间间隔。相应的指标计算结果在表2-5中展示,各数值保留4位有效数字。

表2 Seq2Seq模型在不同训练策略下的指标对比Table 2 Indicator comparison of Seq2Seq model under different training strategies
注意到本文提出的基于MAML策略的预测框架在对传感器数据和历史数据融合更充分的Seq2Seq模型上的表现更优。由于Synthesizer模型是Transformer模型注意力机制即公式(20)中点积计算的轻量化压缩版本,故存在一定的精度损失。同时注意到,虽然各模型在MAML训练策略下均取得了对各指标的提升(部分模型获得了较为显著的提升效果),特别是MAML策略对有较大梯度变化的输出峰片段有更好的拟合效果,但对于梯度变化较小、波动性较为明显的输出峰谷片段的拟合效果提升非常有限。由于分割数据集的随机重组实时性对时序数据造成部分破坏,以及窗口生成机制对早期窗口先期输入、后期窗口末端输入缺失部分自动补全的失真影响,使得MAML策略的预测结果相比“预训练-微调”策略,预测片段存在更明显的毛刺和噪音。
由上述结果可见,本文提出的基于MAML策略作用在各算例模型时均一定程度上提高了其回归预测指标。结果表明,相比预训练-微调策略会极大受限于切换任务数据集时部分破坏了数据的时序依赖导致拟合难度增加等问题,MAML策略因具备基于构建综合任务体随机抽取任务集合快速训练并对新类型数据有效适应的学习能力,从而部分缓解了上述弊端,提升了模型的泛化能力。

表3 CNN-LSTM模型在不同训练策略下的指标对比Table 3 Indicator comparison of CNN-LSTM model under different training strategies

表4 Transformer模型在不同训练策略下的指标对比Table 4 Indicator comparison of transformer model under different training strategies
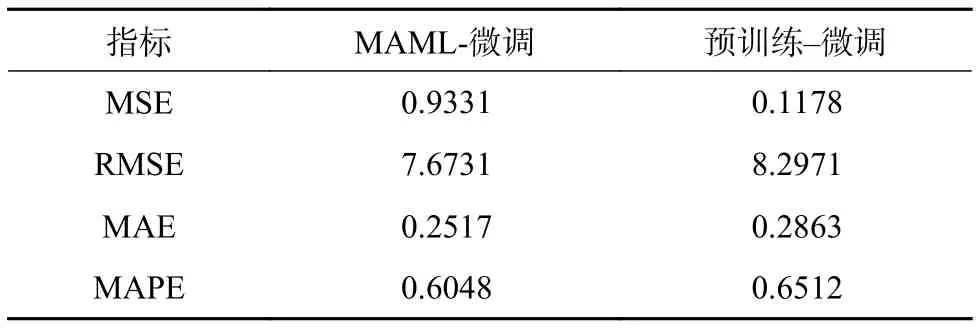
表5 Synthesizer模型在不同训练策略下的指标对比Table 5 Indicator comparison of synthesizer model under different training strategies
3 结论
本文针对电力时序数据的多任务预测问题,构建了基于MAML策略的新型回归预测训练框架。该框架应用在带有注意力机制的Seq2Seq和CNN-LSTM预测模型后,实验结果表明相比预训练-微调方法,具有良好的迁移能力和一定的工程价值,能够快速改造已有模型,进一步取得泛化性更好、预测精度更高的实际效果。
未来工作将进一步在小样本数据缺失、非平衡时序数据、复杂任务等工况下研究动态窗口设计、扩展部署模型等工作。
(本刊附录请见网络版,印刷版略)
附录 A
式中: N 为数据的批大小

附表 A1 算法1:基于MAML策略的数据集生成流程Table A1 Algorithm 1: The generation procedure for datasets based on MAML strategy

附表 A2 算法2:基于MAML策略的短时回归预测训练流程Table A2 Algorithm 2: The regression training procedure for MAML based short term prediction

