基于混合麻雀算法改进反向传播神经网络的短期光伏功率预测
常东峰,南新元
(新疆大学电气工程学院,新疆维吾尔自治区 乌鲁木齐市 830047)
0 引言
随着大量的不可再生能源被开采利用,资源短缺问题愈发严重,为应对能源危机,世界各国都在努力寻找可再生能源,太阳能因储量巨大、清洁环保而倍受关注,利用太阳能发电已经成为人类解决环境恶化和资源短缺问题的重要手段。但受气象因素的影响,光伏发电具有时变性,并网后会给电网带来诸多不利影响。提高光伏发电功率的预测精度,有利于调度管理人员及时调整调度计划,减少光伏并网后产生的负面影响,从而提高电网的运行效率和稳定性[1-4]。
目前,短期光伏功率预测处于广泛的研究阶段,其研究主要分为以下2类[5]:间接预测和直接预测。间接预测根据电站的详细模块参数、地理信息建模预测,这种方法预测精度虽高,但依赖于太阳辐射强度的复杂模型和详细准确的天气预报信息,仅适用于稳定条件下的预测,当气象条件快速变化时,预测性能会受到很大影响[6-7]。直接预测方法建模简单,只需找出历史训练样本和光伏发电功率映射关系即可得到预测模型,具有很强的非线性拟合能力,反向传播神经网络(back propagation neural network,BPNN)模型很适合光伏发电输出功率预测[8-12]。然而,由于BPNN用梯度下降法训练,容易陷入局部极值,收敛速度慢,预测效果并不好。群智能算法常被用于优化BPNN参数[13],文献[14]提出了一种天牛须算法改进BPNN的短期光伏发电预测模型;文献[15]建立了一种特征提取的萤火虫算法优化BPNN的光伏短期预测模型;文献[16]通过欧式距离公式选取相似日,对训练集进行预处理,通过蚁群算法优化BPNN权阈值建立预测模型。以上文献只利用平均主气象因子选取相似日作为训练集,训练集的选取较为粗糙,精度不高,训练样本无法反映预测日的气象变化特征,并且所选算法参数较多,模型复杂,在非稳定天气精度不高,鲁棒性较差。
麻雀搜索算法(sparrow search algorithm,SSA)作为一种具有稳定性好、全局搜索能力强、参数少等优点的新型群智能优化算法,为解决光伏发电预测这类复杂的全局优化问题提供了一种全新的方法,由于在某些情况下麻雀种群多样性降低,导致预测精度差[17]。
为进一步提高预测模型的精度,本文提出混合麻雀搜索算法(hybrid-SSA,HSSA)对BPNN的权值和阈值进行优化建模。SSA的改进主要体现在2个方面:1)通过精英反向策略增加群体的多样性,提高算法的收敛速度;2)利用模拟退火算法的Metropolis准则[18]提高收敛精度,避免最优个体陷入局部极值。
1 气象特征向量和训练集的选择
1.1 气象特征向量
光伏发电的影响因素众多,过多的非关键因素增加了预测的复杂性,降低了收敛速度和精度,本文选取新疆某光伏电站作为研究对象,采集2020年全年的日发电量和多个气象因素进行相关性分析,利用皮尔逊相关系数公式提取与光伏发电相关性较大的气象因子作为模型的输入,以避免冗余的气象因子影响光伏输出,皮尔逊相关系数公式如下

表1 气象因子与光伏发电量之间的相关系数Table 1 Correlation coefficient between meteorological factors and photovoltaic electricity production
1.2 训练样本选取
现通常将相似日的日平均主气象影响因素作为训练集,因气象因素波动较大,平均主气象因素不能准确反映突变点的气象变化特征,其训练的模型在非稳定天气下的预测精度不高,因此,本文利用欧式距离公式计算时序相似度,逐点筛选训练集。预测点的气象特征和历史样本的气象特征具有相似性,这样筛选出来的训练样本可准确跟踪预测点的气象变化特征,从而提高预测模型的鲁棒性,训练集的选取计算公式如下
式中:Y1、Y2、Y3、Y4分别表示此预测点的光伏电站总辐射、散射辐射、直接辐射、测光法理论功率;Xk1、Xk2、Xk3、Xk4分别表示k条历史样本的光伏电站总辐射、散射辐射、直接辐射、测光法理论功率。将欧式距离{d1,d2,···,dn}升序排序,选取前k(1<k≤n)个样本作为预测该时间节点光伏输出功率的训练样本。因为样本数据的单位不一样,一些数据的范围差别很大,导致收敛慢和训练时间长,同时还影响预测精度,为了更精确地预测出结果,要进行归一化处理,使用以下公式处理数据并将其数据区间划定在(-1,1)之间。
式中:y表示历史气象和光伏发电数据归一化后的结果;x表示历史气象和光伏发电原始数据;n和m分别代表历史气象和光伏发电原始数据的最大值和最小值。
2 HSSA-BPNN的搭建与HSSA算法的检验
2.1 HSSA-BPNN模型的搭建
BPNN具有优良的多维函数映射能力,很适合光伏发电预测这类高维度、非线性问题。其结构分为3层:输入层、隐含层和输出层,如图1所示。根据本文1.1节分析结果,以电站的总辐射、散射辐射、直接辐射、测光法理论功率作为BPNN的输入,以光伏发电输出功率作为模型的输出,利用公式(4)选取隐含层节点数。
式中:x和y分别代表输入层和输出层神经元的个数。
BPNN模型的训练主要分2个阶段:输入信号正向传播阶段和误差信号反向传播阶段,输入信号通过输入层输入,经过隐含层传向输出层,当输出值和期望值的差值不满足精度要求时,就会进入误差信号反向传播阶段,输出值和期望值的差值将通过输出层反向传播,通过梯度下降算法调整各层的权值和阈值,如此循环往复,直到输出值和期望值的差值满足精度要求或达到最大迭代次数为止,BPNN训练流程如图2所示。
BPNN采用误差反向传播算法调参,由于其初始的参数选择具有随机性,在训练过程中容易陷入局部最优,因此有必要对BPNN进行改进,以提高模型的预测精度。
利用SSA优化BPNN的模型权阈值建模。算法将种群分成2个群体,一是负责搜索食物并且为其他群体提供食物所在位置的发现者群体,另一个是通过跟踪发现者来觅食的加入者群体。
每次寻优迭代的过程中,发现者的位置根据如下公式进行更新
式中:t表示迭代数;T为最大迭代次数;Xi,j表示第i个麻雀在第j维中的位置信息;α是一个0到1的随机数;R2表示预警值;S表示安全值,其取值区间范围分别为0到1和0.5到1;Q是满足正态分布的随机数;L表示1×d矩阵,且每个元素均为1。当预警值R2小于安全值S时,表示周围安全,麻雀群体不会受到危险,发现者可以进行广泛地搜索;当预警值R2大于或等于安全值S时,表示种群中的一些麻雀已经感觉到周围的危险,并向其他麻雀发出警告,其他麻雀听到警告后迅速转向其他安全区域进行觅食,追随者的位置按照公式(6)进行更新
式中:XP代表此迭代下发现者的最优位置;A表示一个随机赋值为1或-1的1×d的矩阵,A+=代表最劣个体。当i>n/2时,说明适应度值较低的处于饥饿状态的第i个加入者没有获得食物,为获得更多食物,提高自身捕食率,需要到其他地方觅食。当麻雀感觉到危险时,会做出反捕食行为,其数学表达式如下
式中:Xbest代表麻雀粒子最好位置;k是一个随机数,其取值在-1到1之间;β为一正态分布的随机数,其均值为0,方差为1;fg和fw分别表示麻雀种群中最好和最差的适应度值;ε是一个最小常数;fi为麻雀此时的适应度值,当fi>fg时,表示麻雀处在种群边缘,很容易受到危害,fi=fg时,表示麻雀意识到了危险,需要向其他麻雀靠近躲避危险。
由于麻雀种群初始化具有随机性,易聚集同一区域或过于分散,对后面的迭代寻优产生不利影响,利用精英反向策略对种群进行初始化,可以扩大算法的搜索区域,增加群体多样性,提高算法收敛速度。其选择机制如下:
设xi(t)=(xi1,xi2,···,xid)为第t次迭代的一个解,其反向解为xi(t)*,f(x)为目标函数。当f(xi(t))≤f(xi(t)*)时,称xi(t)为第t次迭代的精英个体,说明原解的搜索区域价值高,应加强其领域搜索,当f(xi(t))>f(xi(t)*)时,称xi(t) 为第t次迭代的普通个体,反向解的搜索价值要高于原解的搜索价值,加强反解的搜索区域,设xi,j为普通个体i在j维上的值,则其反向解可定义为
式中:k是介于0~1的随机数;为精英群体所构造的区间,通过在精英群体所构成的动态定义区间上生成普通个体反向解,引导搜索向最优解靠近,提高收敛速度。
为避免寻优迭代过程产生停滞和陷入局部最优,本文将 Metropolis准则与SSA混合,Metropolis准则由模拟退火算法产生,受启发于退火原理,利用该准则以一定概率接受恶化解,对当前解与新解进行比较替换,避免麻雀种群在寻优过程中早熟,提高其全局搜索能力,Metropolis准则的描述如下
式中:Te为当前温度;x是当前麻雀位置;x′是候选麻雀位置,比较P与区间[0, 1]内的随机数,若随机数大于P,放弃候选麻雀位置x′,否则接收x′。
2.2 HSSA-BPNN流程描述
综上所述,HSSA-BPNN的流程如图3所示。具体步骤为:
1)初始化HSSA的R2、n、T、Te等参数;
2)利用精英反向学习策略初始化种群;
3)获取当前最好与最差的麻雀;
4)利用公式(5)—(7)更新麻雀位置并计算适应度(适应度为每次迭代后真实值与预测值的平均绝对百分比误差);
5)利用公式(9)Metropolis准则判定是否接收新解;
6)判定是否达到最大迭代次数,若满足,输出最优麻雀位置,若不满足,跳转至步骤3);
7)将最优麻雀位置赋值BPNN;
8)模型评估。
2.3 算法性能验证
为了验证HSSA的性能,选择了6个经典测试函数,对PSA、蚁群优化算法(ant colony optimization algorithm, ACOA)和SSA进行了对比分析。测试函数如表2所示,其中:f1—f3是单峰函数,用于检验算法的收敛精度;f4—f6是多峰函数,用于检验算法全局寻优的能力,每个算法的设置如表3所示。计算结果通过4个性能指标进行评估。算法独立运行30次的结果如表4所示。单峰测试函数的结果表明,HSSA的收敛精度优于SSA、ACOA和粒子群算法(particle swarm algorithm, PSA)。PSA对f3函数的测试结果较差,但对f6测试函数的测试结果优于ACOA。多峰值测试函数结果表明,HSSA获得了函数f4和f6的理论最优值0,收敛精度优于SSA、PSA和ACOA。传统的SSA、PSA和ACOA的优化结果不稳定。总之,HSSA比其他3种算法具有更高的精度,从而表现出更好的优化能力和稳定性。

表2 测试函数Table 2 Test functions

表3 算法参数设置Table 3 Algorithm parameter settings

表4 测试结果Table 4 Test results
3 示例分析
3.1 构建样本集
实验使用了新疆某光伏电站的数据。选取的样本数据包括2020年1月1日—2020年12月31日时间间隔内的光伏发电数据和相应的气象数据,数据采集分辨率为15min。预测时间周期为08:00—19:00之间的预测功率,根据本文1.1节的分析结果,预测模型的输入变量为总辐射、散射辐射、直接辐射、测光法理论功率。
3.2 预测模型的参数设置
为了验证HSSA-BPNN模型的有效性,另选取了BPNN、PSA-BPNN、SSA-BPNN3种预测模型进行对比分析。各模型训练集的选择,按照欧式距离公式计算得到的时序相似度由大到小的顺序分别选取前1000组作为训练集,选取2020年4月1号至10号作为测试集,各模型对应的输入输出变量相同。为了保证客观性,本文采用抽样误差法,并多次进行对比分析。最后,采用最佳参数值。每个预测模型的参数设置如表5所示,其余参数采用模型的默认值。

表5 参数设置Table 5 Parameter settings
4 结果分析
选取2种具有代表性的天气类型,即晴天、多云转晴天为研究对象。日期为6月10日(晴天)、4月19日(多云转晴天)。4种预测模型在执行20次后的结果被平均,以避免可能的大波动。2种天气类型下,4种预测模型的光伏发电预测值和实际值及2者的相对误差仿真曲线如图4—7所示。2种天气类型下,光伏发电的真实值和4种预测模型预测值及2者的相对误差数据如附表A1—A2。
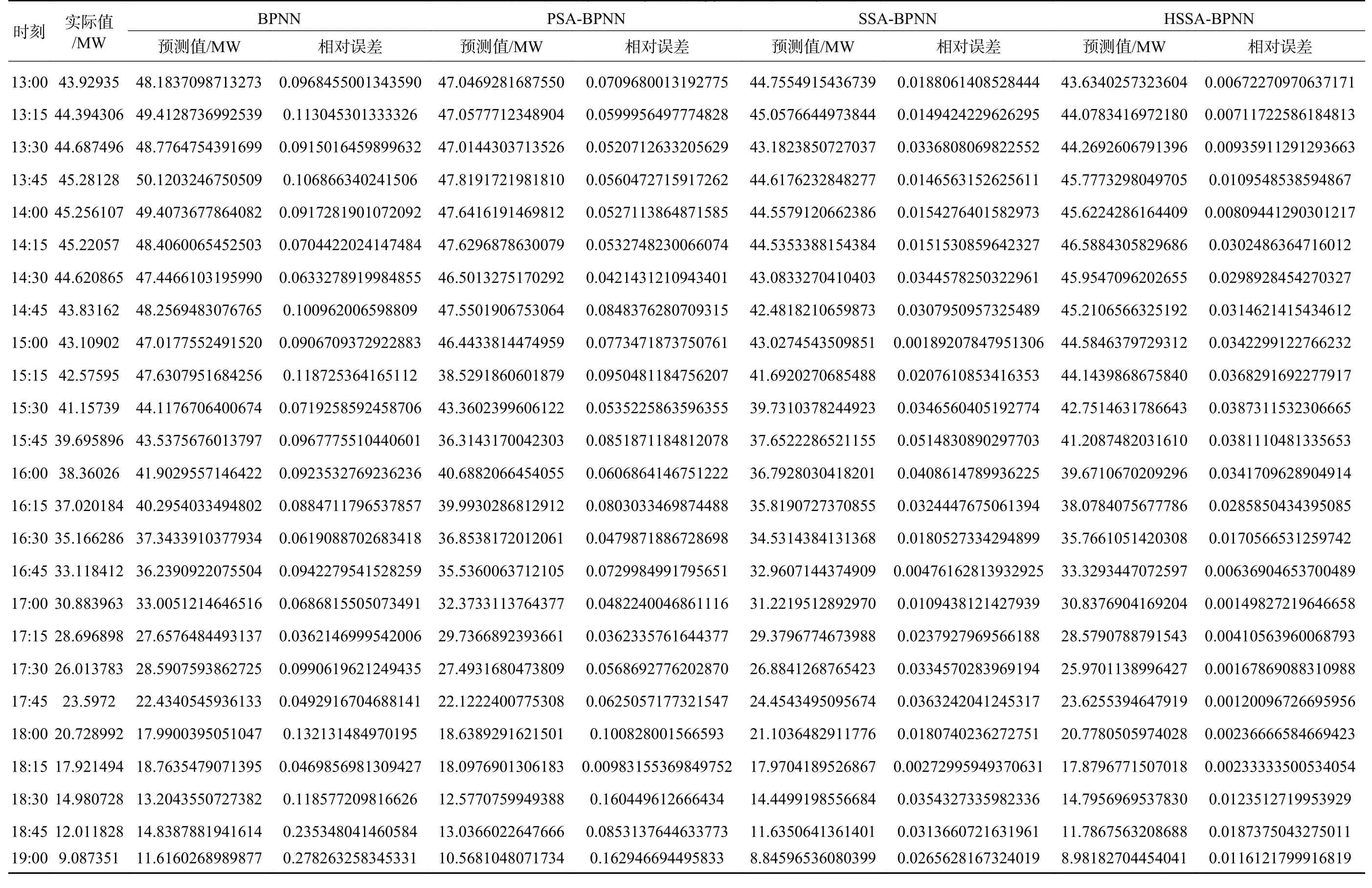
表A1 (续) 晴天天气下不同算法短期预测值及相对误差
图4和图5显示了晴天天气预测的结果。仿真显示,HSSA-BPNN模型的预测结果优于其他3个模型。其他3种模型的预测值和真实值略有偏差,4种预测模型的预测效果都很好,因为光伏发电是有规律的,在晴天波动较小。
图6和图7显示了从多云到晴朗天气的预测结果。图中显示,11:00—14:00多云时段各模型的预测偏差大于14:00—18:00晴天时段的预测偏差。这是由于云的运动导致光伏电站发电功率波动变大,从而增加了预测的难度。HSSA-BPNN模型的预测效果优于其他3种模型。
图8显示了4种模型的收敛结果(以晴天为例),HSSA-BPNN模型获得了更高的收敛精度和收敛速度。
5 模型评估
为了准确评价各预测模型的预测性能,采用平均绝对百分比误差(mean absolute percentage error,MAPE)和均方根误差 (root mean square error, RMSE)定量分析各模型的预测效果。
式中:n为样本数;Pi为样本真实值;pi是样本预测值。预测误差的量化结果如表6所示。结果表明,在功率变化稳定的晴天,4种预测方法的预测效果均优于多云转晴天气。所有模型的NMAPE和NRMSE都很小,预测结果都比较准确。由于云的出现和移动降低了每种方法的预测精度,因此在多云到晴天的NMAPE和NRMSE大于晴天。在2种天气类型下,所提出的HSSA-BPNN的误差量化值较小,其预测效果优于其他3种方法,具有良好的环境适应性。晴天天气下,HSSA-BPNN模型的NMAPE相对于SSA-BPNN、PSA-BPNN和BPNN模型的NMAPE分别下降了约60.18%、80.5%和87.3%;NRMSE比其他3种方法分别下降了约28.1%、68.1%和78.0%。多云转晴天气下,HSSABPNN模型的NMAPE相对于 SSA-BPNN、PSABPNN和BPNN模型的NMAPE分别下降了约49.4%、74.0%和82.7%;NRMSE比其他3种方法分别下降了约52.1%、73.4%和81.7%。同时,从实验误差指标值可知,在确定预测模型的输入变量和结构参数时,HSSA-BPNN的NMAPE值是固定值,具有良好的预测稳定性。然而,当其他方法在相同的条件下用于多次预测时,每次预测的结果幅度都不同,稳定性差。收敛速度方面,HSSABPNN模型在第10次收敛到适应度最佳,而SSABPNN、PSA-PBNN模型和BPNN模型搜索过程中陷入局部最优,并且收敛速度慢。由此验证HSSABPNN具有较好的全局寻优能力和收敛速度。

表6 模型评估Table 6 Model evaluation
6 结论
1)根据皮尔逊相关系数公式分析结果,将总辐射、散射辐射、直接辐射、测光法理论功率作为预测模型的输入,降低了预测模型的复杂性,有效避免了气象因素的冗余问题。
2)结合皮尔逊相关分析的结果,利用欧氏距离公式计算时序相似度精准地选取训练样本,训练样本准确跟踪了预测时间节点的气象变化特征,提高了训练样本可靠性。
3)精英反向学习策略和Metropolis准则引入麻雀算法分别用于初始化SSA种群和改进SSA更新策略,提高了麻雀算法的收敛速度和避免了麻雀种群在寻优迭代过程中陷入局部最优。
4)本文提出的HSSA-BPNN预测模型与SSABPNN、PSA-BPNN、BPNN等3种经典方法进行了比较分析,分析结果表明,晴天天气下NMAPE和NRMSE分别为仅为1.31%和0.7244,多云转晴天气下NMAPE和NRMSE分别仅为2.14%和0.9451,所提HSSA-BPNN模型的误差指标在2种天气下均低于其他3种方法,由此验证了HSSA-BPNN模型具有良好的适应性、较好的预测性能。
(本刊附录请见网络版,印刷版略)
附录 A

附表A1晴天天气下不同算法短期预测值及相对误差Table A1 Short-term prediction values andrelative errors by different algorithms in sunny weather

附表A2 多云转晴天气下不同算法的短期预测值及相对误差Table A2 Short-term prediction values andrelative errors by different algorithms in cloudy then turn sunny

表A2 (续) 多云转晴天气下不同算法的短期预测值及相对误差

