超冷原子系统中电磁诱导透明的弱光矢量怪波

秦璐，冯雪景，蒋亚静，齐文荣，田红娟，赵兴东,夏世强，杨春洁，张计才，高玉峰，朱遵略，刘伍明

(1.河南师范大学 a.物理学院；b.计算机与信息工程学院,河南 新乡 453007；2.中国科学院 物理研究所 北京凝聚态物理国家研究中心,北京 100190)

怪波(Rogue Wave)是一种在空间和时间上局域的具有很高振幅的波.它来无影、去无踪的特性使其具有很强的破坏性,所以在理论和实验上，怪波的许多问题都值得深入研究.近年来，不同的物理体系中相继发现怪波，包括水槽系统[1]、光纤及谐振腔[2-7]、玻色-爱因斯坦凝聚(Bose-Einstein Condensation，BEC)[8-10]以及金融领域[11]等.关于怪波的成因，通常认为是调制不稳定性(Modulation Instability,MI)将一定范围的初始频率放大引起的，导致其远远大于初始振幅.2007年，SOLLI等人[12]首次在非线性光纤中观察到光学怪波，打开了光学怪波研究的大门，光学怪波由于其广泛的应用而备受人们的关注.

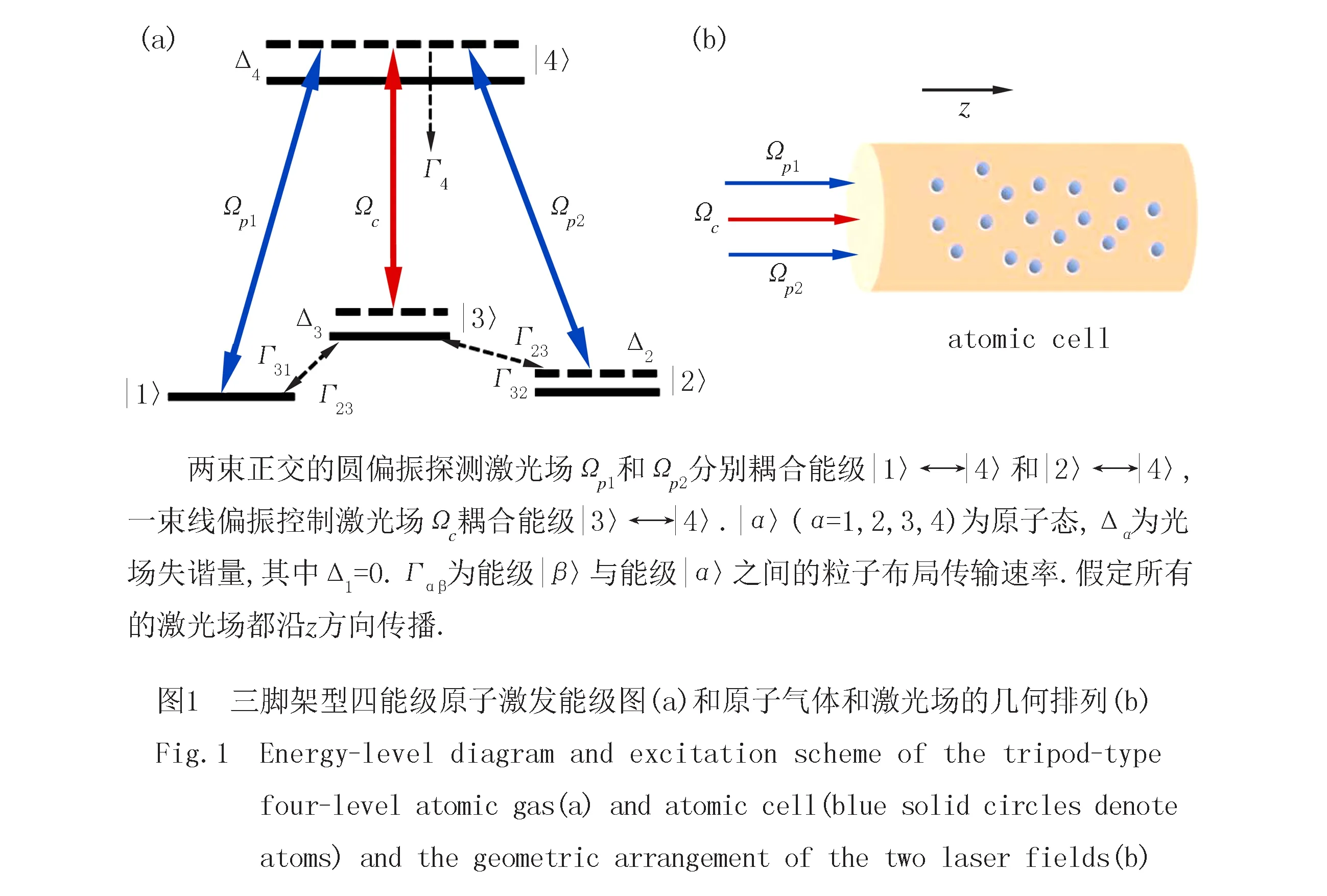
非线性薛定谔方程(Nonlinear Schrödinger Equations,NLS)可以作为一种简单的物理模型来分析光学怪波，而多分量耦合的非线性薛定谔方程可研究不同偏振分量的矢量怪波.本文在三脚架型四能级冷原子体系实现了双分量光学怪波，其中两束弱探测场和一束强控制场分别耦合原子能级.由于体系电磁诱导透明效应，该体系可以在较弱的功率下实现矢量光学怪波.通过调节原子系统的参数，可实现亮-亮矢量怪波、暗-暗矢量怪波和亮-暗矢量怪波.

1 模型简介

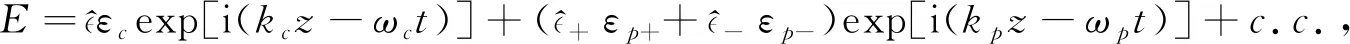
在电偶极近似和旋转波近似下，原子系统在相互作用绘景下的哈密顿量为

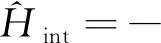
(1)

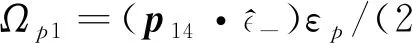
原子动力学满足光学布洛赫方程

(2)

其中ρ是一个4×4密度矩阵，密度矩阵元为ραβ(α,β=1,2,3,4)描述原子布局和相干.Γ是一个4×4相干弛豫矩阵，描述系统的自发辐射和退相干.假设控制光场强度远远大于探测光场，因此不考虑控制光场的动力学.探测光场的动力学由麦克斯韦方程描述，在慢变包络近似下可以写为

(3a)

(3b)

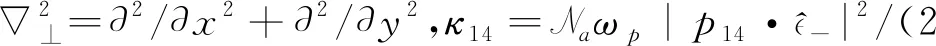
2 线性色散关系

考虑到实验实现的可能性，这里选取激光冷却的87Rb原子气体，其能能级结构为：|1〉=|52S1/2,F=1,mF=1〉,|2〉=|52S1/2,F=1,mF=-1〉,|3〉=|52S1/2,F=1,mF=0〉和|4〉=|52P3/2,F=2,mF=0〉.自发辐射衰退Γ4≈2π×6.06 MHz,Γ3≈2π×3.2 kHz,Γ13≈Γ23=Γ3/2,Γ14≈Γ24≈Γ34=Γ4/3.

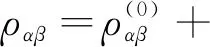
(4a)

(4b)

其中Dj(ω)=|Ωc|2-(ω-d3j)(ω+d4j)(j=1,2).

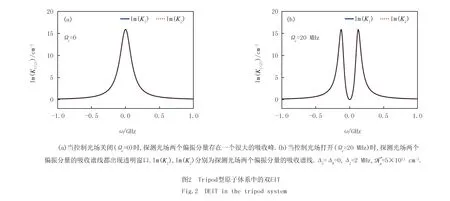
如图2是探测光场两个偏振分量吸收谱的Im(K1)和Im(K2)随频率ω变化图.当控制场关闭时(图2(a))，探测光场的两个偏振分量的吸收谱线存在一个很大的吸收峰.当控制光场打开时(图2(b))，探测光场的两个偏振分量的吸收谱线出现透明窗口.

为了讨论探测光场两个偏振分量的非线性效应，应该考虑高阶情况.在二阶解中，Ωp1和Ωp2的可解条件满足i[∂Fj/∂z1+(1/Vgj)∂Fj/∂t1]=0(j=1,2),其中Vgj=1/K1j(K1j=∂Kj/∂ω)为探测光场j分量的群速度.

在三阶解中，系统中的克尔效应会产生很重要的作用.推导得到探测光场两个偏振分量的非线性包络函数F1和F2满足的可解条件

(5a)

(5b)

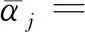
考虑原子的能级寿命是有限的，非线性薛定谔方程中的系数都是复数形式.但是由于EIT效应存在，系数的虚部都远远小于实部，可以忽略不计.通过定义ζ=z/LD，τ=(t-z/Vg)/τ0,u1=(Ωp1/U0)exp(-iK1z),u2=(Ωp2/U0)exp(-iK2z),耦合非线性薛定谔方程转化为无量纲形式

(6a)

(6b)

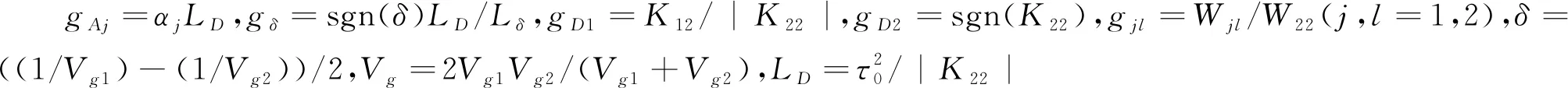
3 矢量怪波解

由于控制光场诱导的EIT效应，因此方程(6)中的复系数的虚部可以忽略.这使得方程(6)几乎是可积的，因此系统支持矢量怪波解.当忽略系数的虚部时，方程(6)很容易得到亮-亮，亮-暗和暗-暗怪波解.

通过选择合适的系统参数，方程(6)中无量纲参数gδ=0.001,gD1=-1,gD2=-1,g11=g12=g21=g22≈-2.此时系统非线性为自聚焦非线性.上式方程即成为矢量非线性薛定谔方程(Vector Nonlinear Schrödinger Equations,VNLS)或Manakov 系统

(7a)

(7b)

利用标准的达布变换[13-15]求解聚焦矢量非线性薛定谔方程(7)可得到有理解，即怪波解

(8)

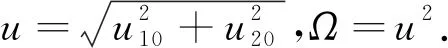
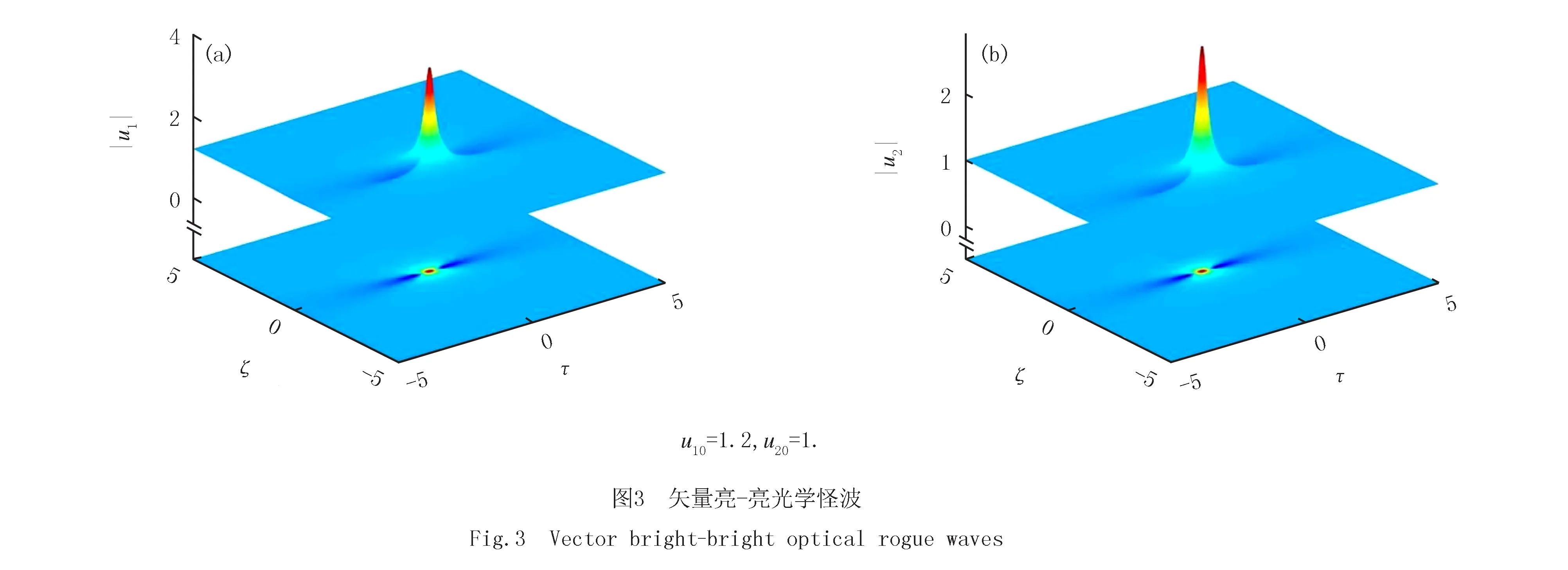
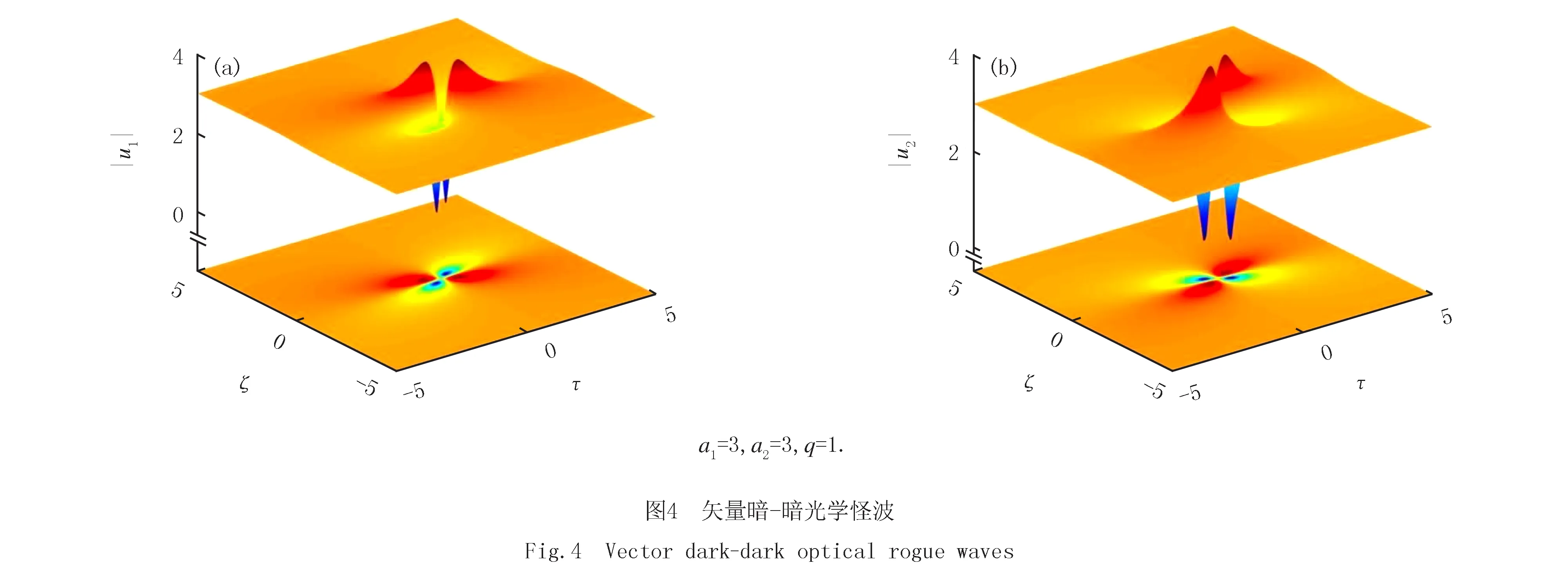
与传统的固态系统相比，超冷原子系统的一大优势就在于其易于操控.选择合适的系统参数，非线性薛定谔方程无量纲参数gδ=0.001,gD1=-1,gD2=-1,g11=g12=g21=g22≈2,此时系统非线性为自散焦非线性[16-17].在自聚焦条件下，矢量非线性薛定谔方程支持亮怪波解.在自散焦条件下，非线性薛定谔方程支持暗怪波.利用标准的达布变换[13-15]，可得到矢量自散焦非线性薛定谔方程的怪波解

(9)

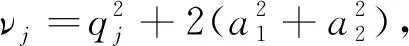
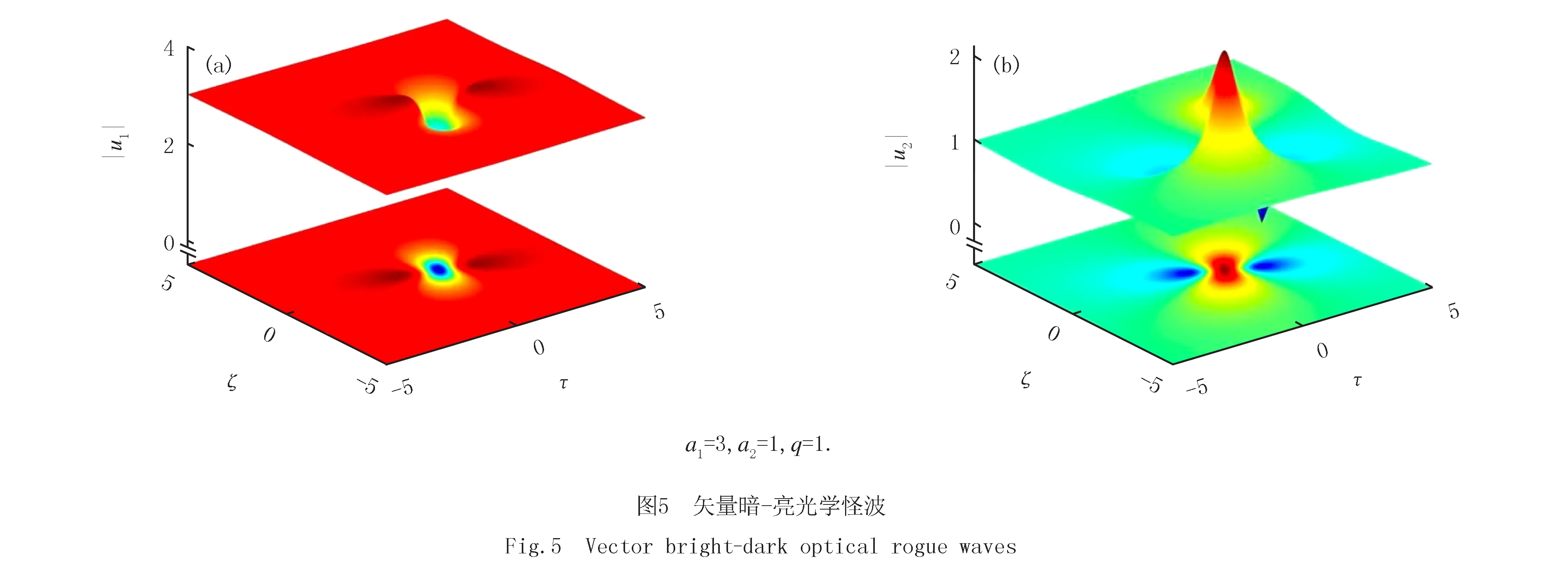
选择不同的初始输入参数，体系支持暗-亮怪波解.如图5所示，探测场两个偏振分量的峰值强度分布，其中a1=3,a2=1,q=1.观察发现探测光场一个偏振分量|u1|在(τ,ζ)=(0,0)位置，其峰值下陷至最小值，即暗怪波.探测光场另一个偏振分量|u2|在(τ,ζ)=(0,0)位置，具有极高的峰值，即亮怪波.

4 调制不稳定性

关于怪波的起因，目前有很多不同的猜测.调制不稳定性被认为是诱导怪波的一种重要机制，它可以将一定范围的初始频率放大，这部分放大频率所对应波的振幅随着演化将越来越大，并最终远远大于初始振幅[18-20].

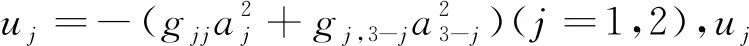
(10)

其中αj和βj为扰动部分的复振幅，δ为无量纲的波矢，λ为扰动的增长率.

将调制的平面波(10)式代入到无量纲的耦合非线性薛定谔方程(7)中，保留αj和βj的线性部分可以得到扰动增长率

(11)

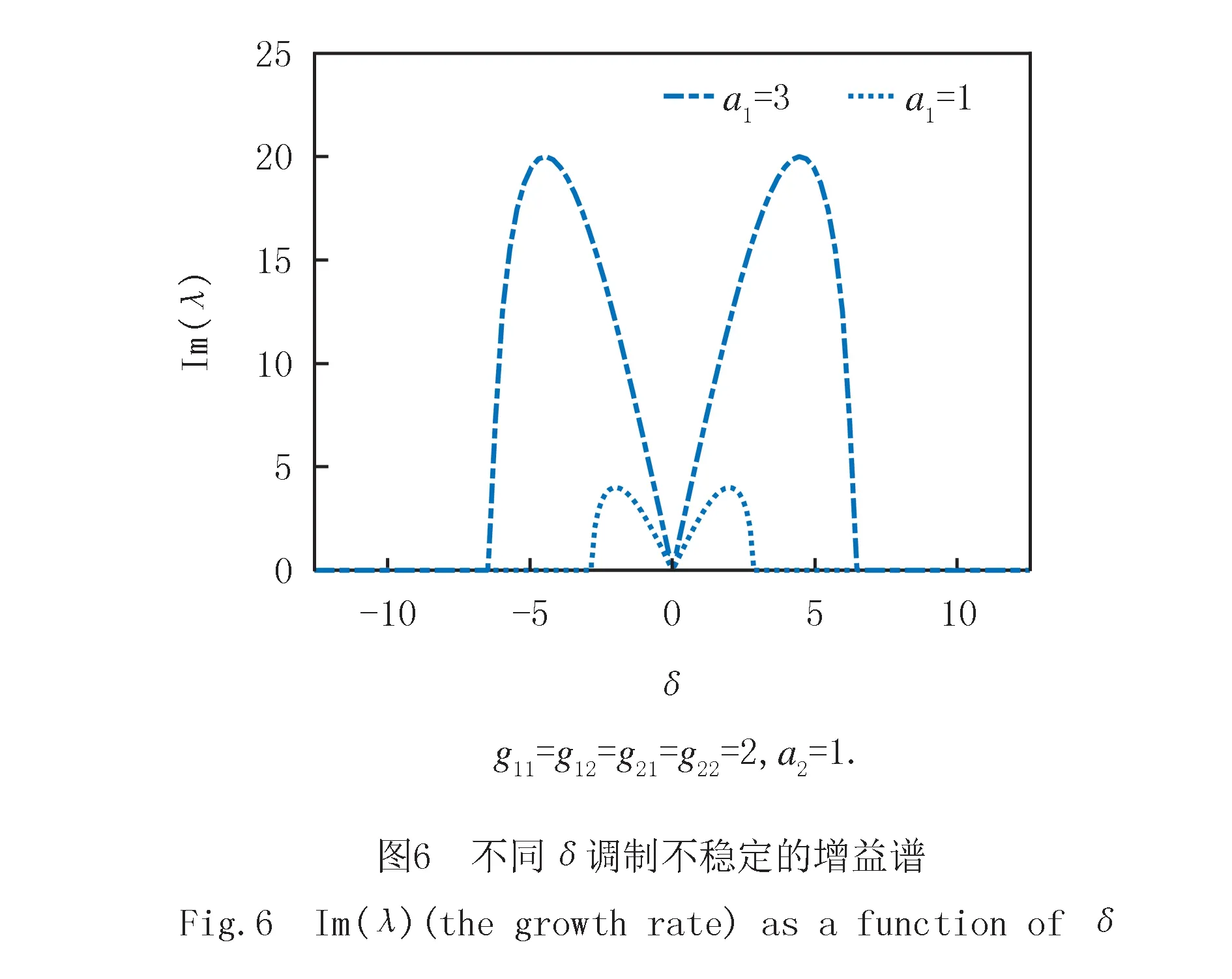
扰动增长率有虚部出现时，平面波背景不稳定，即为产生怪波的条件.如图6所示，在一定的δ区间，扰动增长率存在，对这些频率下的扰动，稳态解是不稳定的，可以发生调制不稳定性.

5 结 论

在许多物理系统中都发现怪波现象，为了详细研究怪波的成因，遏制其带来的危害.本文提出在冷原子系统中研究光学怪波，通过解析推导及数值模拟，得到了非线性条件下的光学怪波.进一步的研究发现通过调节系统参数，双分量模型可以实现亮-亮怪波，暗-亮怪波和暗-暗怪波.此外，通过调制不稳定分析，详细地研究产生光学怪波的条件，有助于对非线性系统的不稳定性本质和动力学有更深刻的理解，并发现其在光学信息处理和光学传输方面的潜在应用.