直升机自主抗干扰姿态控制方法

聂文明，史青海，梅 彬

(中国直升机设计研究所，江西 景德镇 333001)

0 引言

直升机自身气动力学复杂，存在非线性强、通道间耦合严重、飞行环境多变等特点，目前仍无法获得综合考虑机身、旋翼等气动力学的准确模型，这也使得直升机的飞行控制面临巨大挑战。一方面，直升机构造复杂，模型参数偏差显著；另一方面，实际飞行环境中存在阵风等未知干扰。这两方面对直升机姿态动力学的影响显著，因此需要研究具备抗干扰能力的姿态控制方法。在现有飞行控制方法中，动态逆方法和最优控制方法虽被广泛研究，但均依赖于被控系统的精确模型，抗干扰性能较差；反步法和鲁棒控制方法虽能增强控制系统的鲁棒性，但也会导致控制系统存在较大保守性。如何在降低控制系统设计对模型的依赖的同时，增强控制系统的抗干扰性能，是直升机姿态控制领域亟待解决的问题。

针对上述问题，本文考虑模型参数偏差和外部干扰导致的模型不确定性，基于扩张状态观测器(extended state observer, ESO)和动态逆理论，提出了一类直升机自主抗干扰姿态控制方法，不仅显著提高了控制系统的抗干扰性能，实现了存在模型不确定性情况下的高精度、无超调、快速的姿态控制，而且由于控制系统的设计是基于ESO对模型不确定性的在线自主观测值，而非模型不确定性的上界假设，因此既降低了控制系统设计对模型的依赖，又不会导致设计中的保守性。

1 直升机姿态运动模型

本文以UH-60为研究对象，在不考虑模型参数偏差及外部干扰的情况下，其横侧向姿态标称运动模型可表示为如下形式：

(1)

其中，=[，]∈，=[，]∈为状态量，分别表示滚转角、偏航角、滚转角速率、偏航角速率；=[，]∈为控制量，分别表示横向周期变距和尾桨距；∈，∈分别为系统矩阵。

然而在直升机的实际建模与飞行中，一方面由于直升机自身飞行力学的复杂性及建模过程中引入的假设，直升机建模中不可避免存在模型参数偏差；另一方面，直升机实际飞行中需面对如风场干扰等未知外部干扰，直接影响直升机飞行力学特性，进一步导致直升机动力学模型存在外部干扰引起的模型偏差。综上，在考虑模型参数偏差及未知外部干扰的情况下，式(1)所示的标称模型可完善为如下形式：

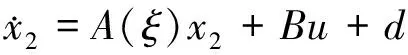
(2)

其中，表示模型参数偏差，∈表示未知外界干扰，两者对直升机动力学造成的未知模型不确定性为控制器设计带来了较大困难。

为改善直升机姿态控制器性能，本文基于ESO和动态逆理论提出了一种直升机自主抗干扰姿态控制方法，实现了对模型不确定性的在线实时观测，解决了存在直升机的多源不确定性情况下的姿态控制问题，显著改善了姿态控制器的抗干扰性能。

2 自主抗干扰姿态控制算法设计

本节首先基于ESO，设计了模型不确定性的在线自主观测器；并结合在线观测得到的模型不确定性观测值，设计了直升机横侧向姿态控制算法，进一步基于Lyapunov理论，给出了观测误差渐进收敛性的理论证明。

2.1 基于ESO的总干扰观测算法设计

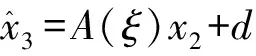
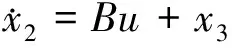
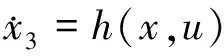
(3)

=

(4)

其中，=[,,]∈为增广后的状态量，表示模型输出量，总干扰视为模型的扩张状态，上述两式共同构成扩张状态模型。为实现总干扰及各状态量的自主观测，设计模型(3)的ESO如下：

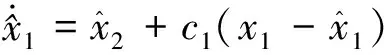
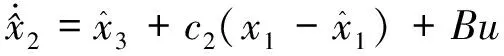
(5)

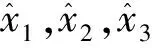
假设可通过参数整定，使得ESO实现对总干扰的高精度观测，则姿态控制律可设计为如下形式：

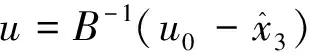
(6)

则原姿态动力学模型(2)可近似为如下形式：

(7)

至此，可通过简单的状态反馈设计标称控制器，实现期望的控制性能。

2.2 ESO观测误差收敛性分析

设定ESO增益参数如下：

(8)

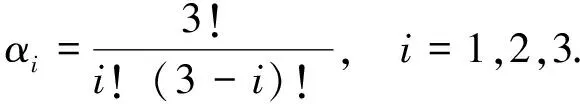
(9)

则ESO特征多项式即可满足下式：

(10)

至此，ESO的增益整定问题就被转化为观测器带宽的设计问题，即仅需整定一个参数即可完成ESO的整定。

假设(,)为相对于的全局Lipschitz函数，则存在一常数∈(1,+∞)，当ESO带宽满足∈(,+∞)时，ESO观测误差将渐进收敛至0，即：

(11)

在(,)函数关系已知的情况下，式(5)所示ESO可为如下形式：

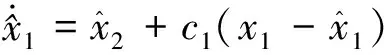
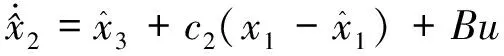
(12)

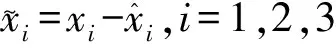
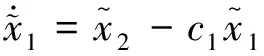
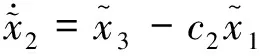
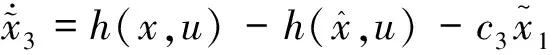
(13)

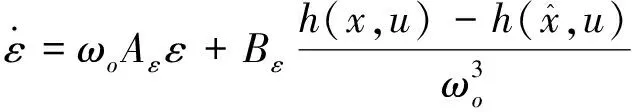
(14)

其中，，分别如下：

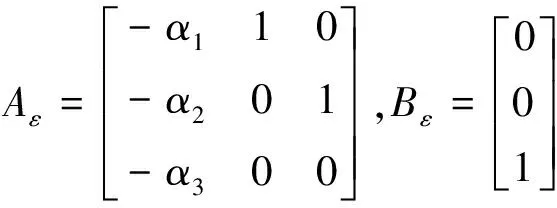
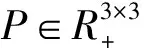
构造Lyapunov函数如下：

=

(15)

则可推导得到关于时间的导数如下：

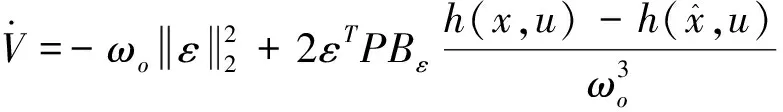
(16)

因(,)是关于的全局Lipschitz函数，故存在某一常数使得如下不等式成立：

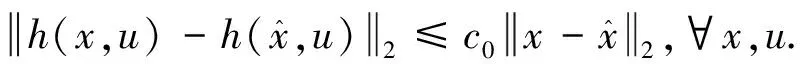
(17)

若≥1，则式(16)等号右侧第二部分可进一步推导如下：

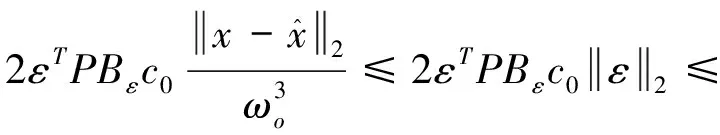
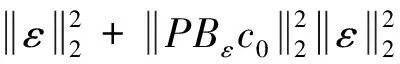
(18)

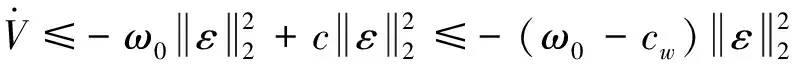
(19)

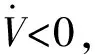
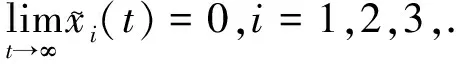
证毕。

3 仿真分析

本节通过数值仿真，进一步验证所提出的直升机自主抗扰姿态控制方法的有效性，主要进行两方面的仿真：①自主抗干扰控制方法与传统控制方法的仿真对比，验证相较传统方法，自主抗干扰控制方法对姿态控制性能的改善；②针对直升机模型存在3种不同不确定性的情况，验证自主抗干扰控制方法的控制性能。

仿真环境采用matlab2016b，仿真基于文献[8] 提供的UH-60直升机前飞状态(前飞速度20 kt)数学模型展开。仿真中采用的状态量初始值等各项参数如表1所示。

表1 仿真相关参数设置

3.1 与传统姿态控制方法的对比仿真

仿真试验中，针对存在外部干扰的情况，对如表2所示两类控制方法进行控制性能对比。

表2 仿真工况及控制方法统计表

仅考虑外部干扰的情况下，对应式(2)所示的实际姿态动力学模型中各项模型不确定性为=0,≠0，考虑如下形式的外部干扰：

=[3sin3cos]

(20)

图1-图6给出了两种控制方法的仿真结果，其中图1-图4为姿态角及姿态角速率响应曲线，图5-图6为变距量响应曲线。

由图1-图4的黑色虚线可以看出，在无干扰情况下，两种控制方法的控制性能均较好，均能实现对红色虚线所示姿态指令值的高精度、快速跟踪。然而，由图1-图4的蓝色实线可以看出，当有式(20)所示的外部干扰作用于直升机姿态动力学时，传统控制器的性能显著下降，而本文所提出的自主抗干扰控制器依然能够保证自身控制性能，依然可以实现直升机姿态的高精度、快速稳定控制，完成对姿态指令值的跟踪。具体控制精度、调节时间、超调量的数据见表3。

表3 控制性能指标统计表

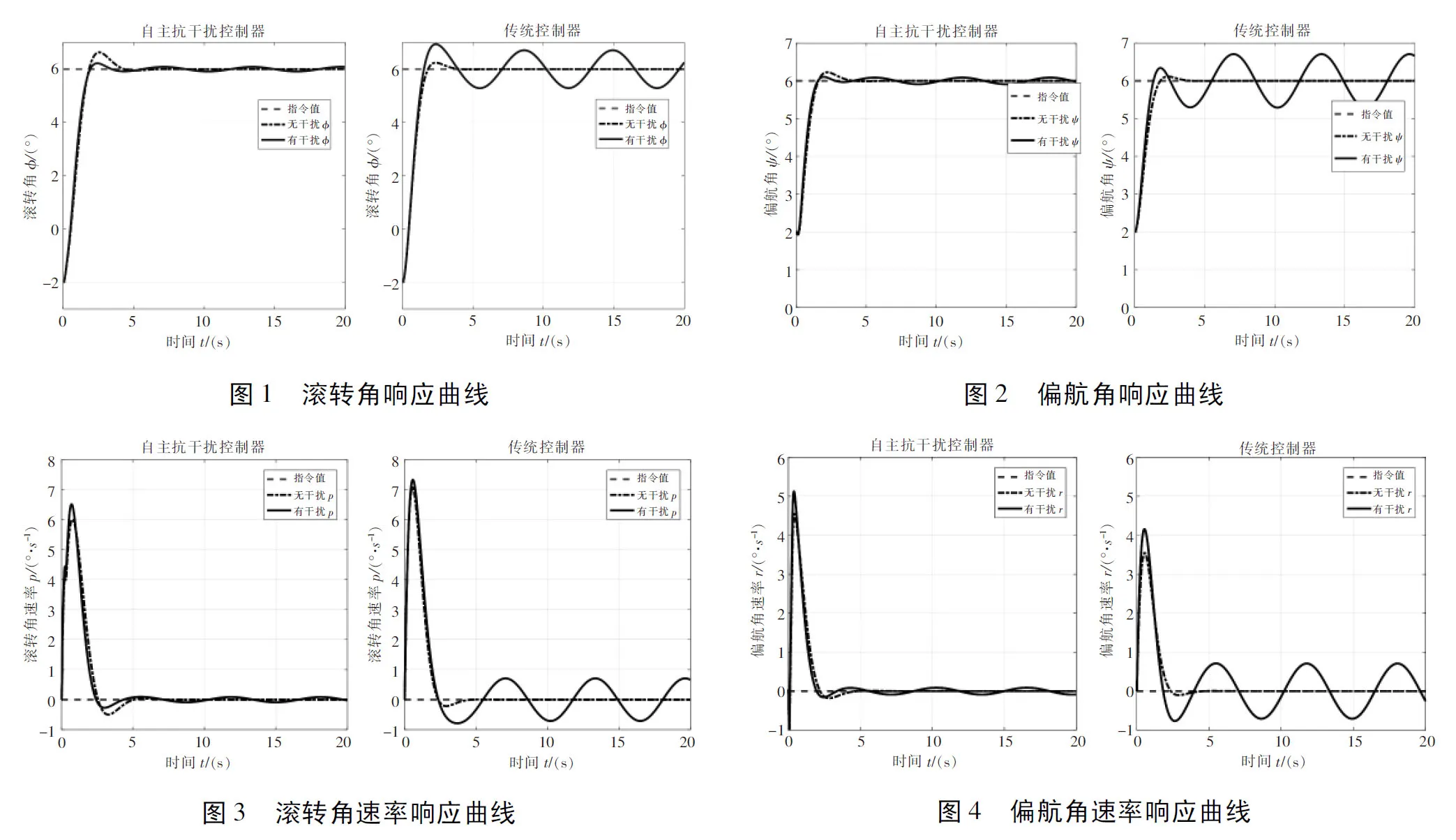
由图5-图6可以看出，与传统控制方法相比，本文所提的自主抗干扰姿态控制方法并未导致过大控制量需求。

图7给出了各姿态角及姿态角速率的实际值与ESO观测值的对比曲线。为充分验证ESO的性能，设置ESO的观测状态(蓝色虚线)初始值与状态量实际初始值之间存在±2°的误差。可以看出，ESO可以在0.1 s内消除观测误差，实现对实际状态量的高精度近似，且全程观测精度均较高。

图7 ESO观测结果

3.2 不同模型不确定性情况下的控制方法性能仿真

设置三类不同，如表4所示。

表4 模型不确定性设定表

图8给出了考虑三种模型不确定性情况下的控制器仿真结果。从图中可以看出以下结论：

图8 三种不确定性情况下的状态量响应曲线

1)三种情况下的仿真曲线略有不同，说明模型参数偏差、外部干扰对直升机姿态动力学均有显著影响，因此设计具备较强抗干扰能力的姿态控制方法具有重要意义；

2)结合表5与图8可知本文所提自主抗干扰姿态控制方法的控制性能无明显差别，该方法的抗干扰能力适用范围较广。

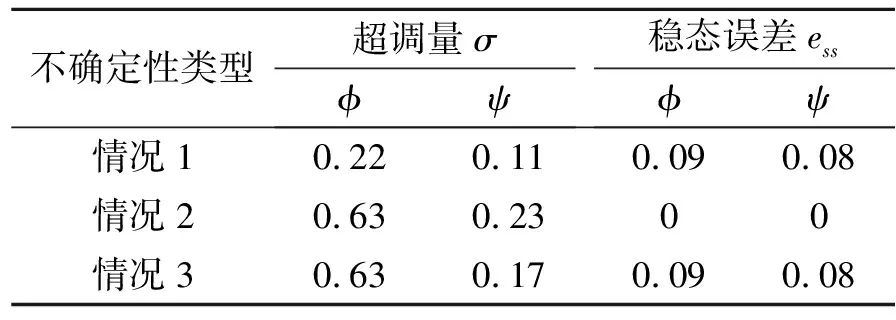
表5 不同模型不确定性情况下的控制性能指标统计表

4 结论

直升机动力学模型复杂度高、非线性强，且存在模型参数偏差以及外界干扰导致的未知不确定性，难以建立准确的动力学模型，给姿态控制性能的提升带来的困难；另一方面，随着飞行任务的复杂化，对控制方法的性能提出了更高的要求。本文提出了基于ESO的直升机自主抗干扰姿态控制方法，可通过在线自主观测的方式，获得模型不确定性的高精度观测值，显著改善了姿态控制性能，降低了姿态控制方法设计对模型的依赖；并且分别从理论分析和数值仿真验证的角度，验证了所提出的模型辨识算法的收敛性、快速性和高辨识精度等性能。此外，本文所提出的姿态控制方法结构简单，易于工程实现，为解决多源不确定性情况下的高性能姿态控制问题，满足新型任务的控制性能需求提供了可供参考的途径。