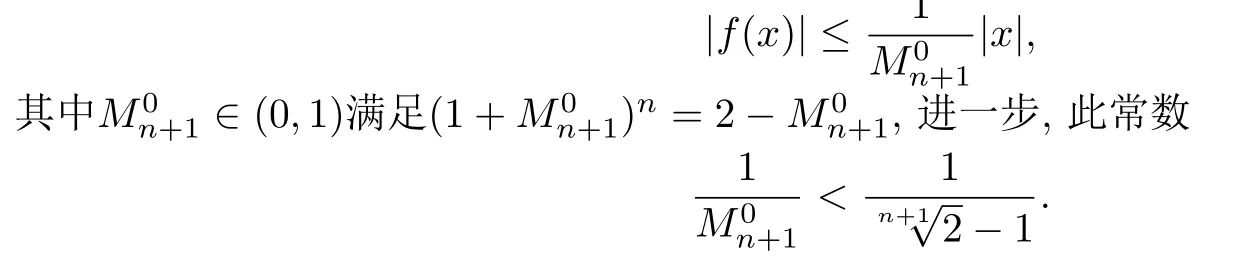Clifford分析中带有精确常数的Schwarz引理

王海燕，孙宁馨，边小丽

(天津职业技术师范大学 理学院，天津 300222)

§1 引言

Schwarz引理是复分析中最基本的定理之一，它揭示了解析函数的几何特性.Ahlfors第一次将几何概念引入了Schwarz引理[1-2]，Yau于1978年将其推广到Kähler流形[3].近几年来，Schwarz引理逐步推广到非交换空间.文献[4]给出了一般欧氏空间中的Schwarz引理，张忠祥在文献[5-6]基于Poisson积分公式建立了Clifford分析中Dirac算子对应的Schwarz引理，并通过Möbius变换给出了Clifford分析中的Schwarz-Pick引理，为在Clifford分析中研究正则函数的几何特性奠定了基础.文献[7]将该结果推广到非交换，非结合空间中，文献[8]基于Cauchy积分公式给出了低维空间中与Helmholtz算子相关的Schwarz引理，文献[9]将Schwarz引理推广到Slice Clifford分析.

基于以上结果，本文首先从Poisson积分公式出发，给出了文献[6]中Schwarz引理的推广形式，然后利用Cauchy积分公式和Hile引理，建立了Clifford分析中带有精确常数的Schwarz引理(如下)，对低维通过画图直观地展示了该方法得到的常数优于基于Poisson积分公式得到的结果，对一般情况进行了详细的证明.

主要结果设B(0，R1)⊂Rn+1，函数1(B(0，R1)，Cl(n))满足f(0)0，Df(x)0，|f(x)|≤R2，(0，R1)，则对任意的(0，R1)，有

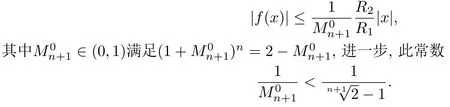
§2 预备知识

设e1，e2，···，en是n-维实向量空间Rn上的标准正交基.引入乘法运算，满足

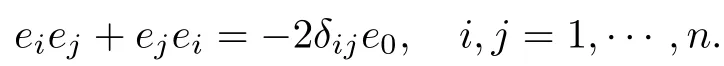
在该乘法下它们生成了非交换可结合的Clifford代数，记为Cl(n)[10-15].

通常e0等同于实数1，实数空间R可以视为Clifford代数Cl(n)的子空间，Rn+1中的元素可以看成一个Clifford数x(x0，x1，...，xn)定义共轭运算，其满足

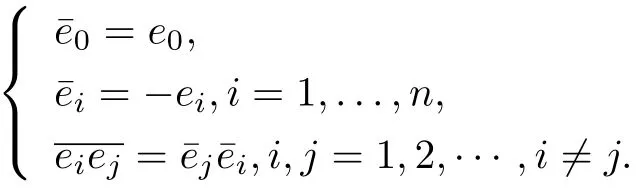
对任意元素Rn+1其共轭为

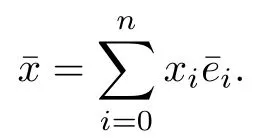
由于

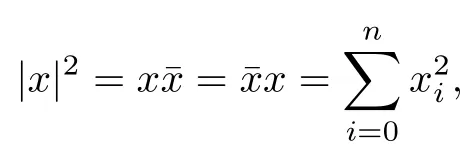
则对任意Rn+1{0}具有逆元素

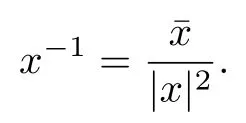
Clifford分析中，一般研究Dirac算子

对于任意Clifford值函数f:Rn+1-→Cl(n)，将其表示为

其中

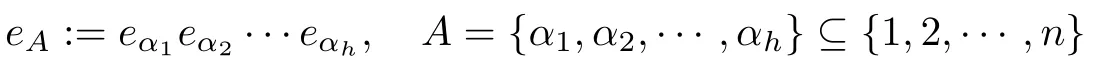
且1≤α1＜α2＜αh ≤n，当A∅时，eA1，fA(x)是实值函数.Dirac算子作用到函数上按照如下规则

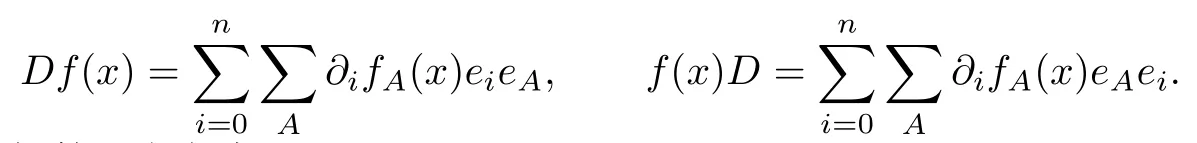
Dirac算子的共轭算子定义为

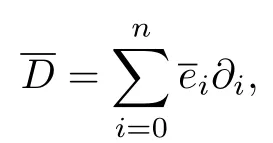
满足

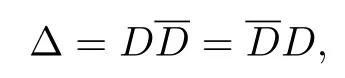
其中Δ是Rn+1中Laplace 算子.Dirac 算子D的基本解(称为Cauchy 核)具有显示表达式

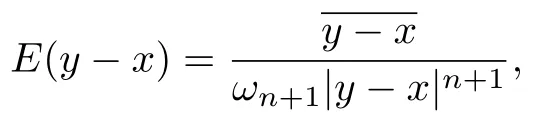
其中

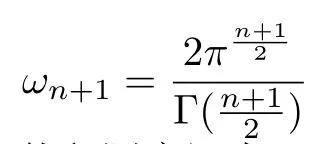
是Rn+1中单位球面的面积.在Rn+1中，体积测度记为

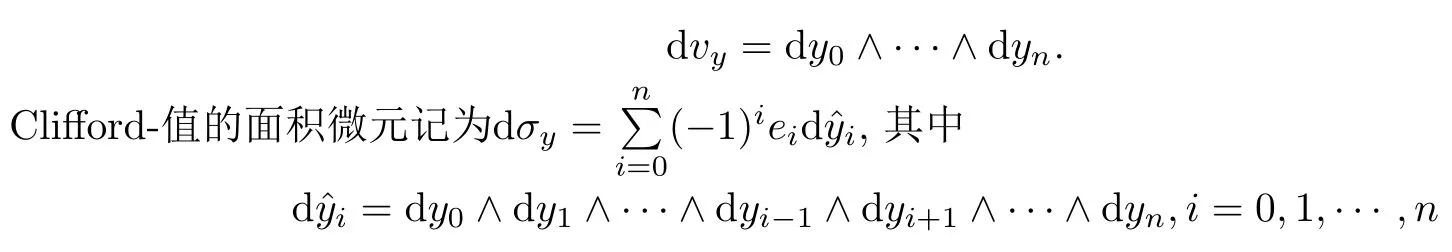
表示从dvy中去掉dyi.Clifford值的面积微元和经典的面积微元dS之间满足

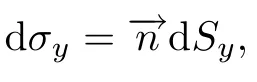
定义2.1在开集U ⊂Rn+1中，若连续可微函数f在U中满足

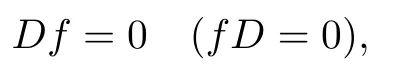
则称f是U中左(右)正则函数.

§3 Schwarz引理

本节给出Clifford分析中Dirac算子对应的Schwarz引理.定理3.1实际上是文献[6]中定理3.1的推广形式，证明方法也如文献所示从Poisson积分公式出发;定理3.2是本文的主要结果，从Dirac算子对应的Cauchy积分公式出发并利用Hile引理，给出了Schwarz引理的精确估计，该定理中出现的常数优于定理3.1的相应常数.

为下文方便地比较两常数，给出文献[6]中定理3.1的推广形式及完整的证明过程.符号B(0，R1) 是Rn+1中，中心在原点，半径是R1的开球，∂B(0，R1)是B(0，R1)的球面.

定理3.1设B(0，R1)⊂Rn+1，1(B(0，R1)，Cl(n))满足

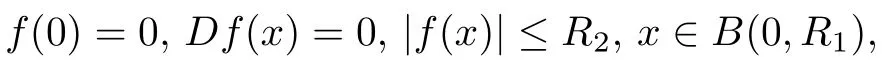
则对任意(0，R1)，有

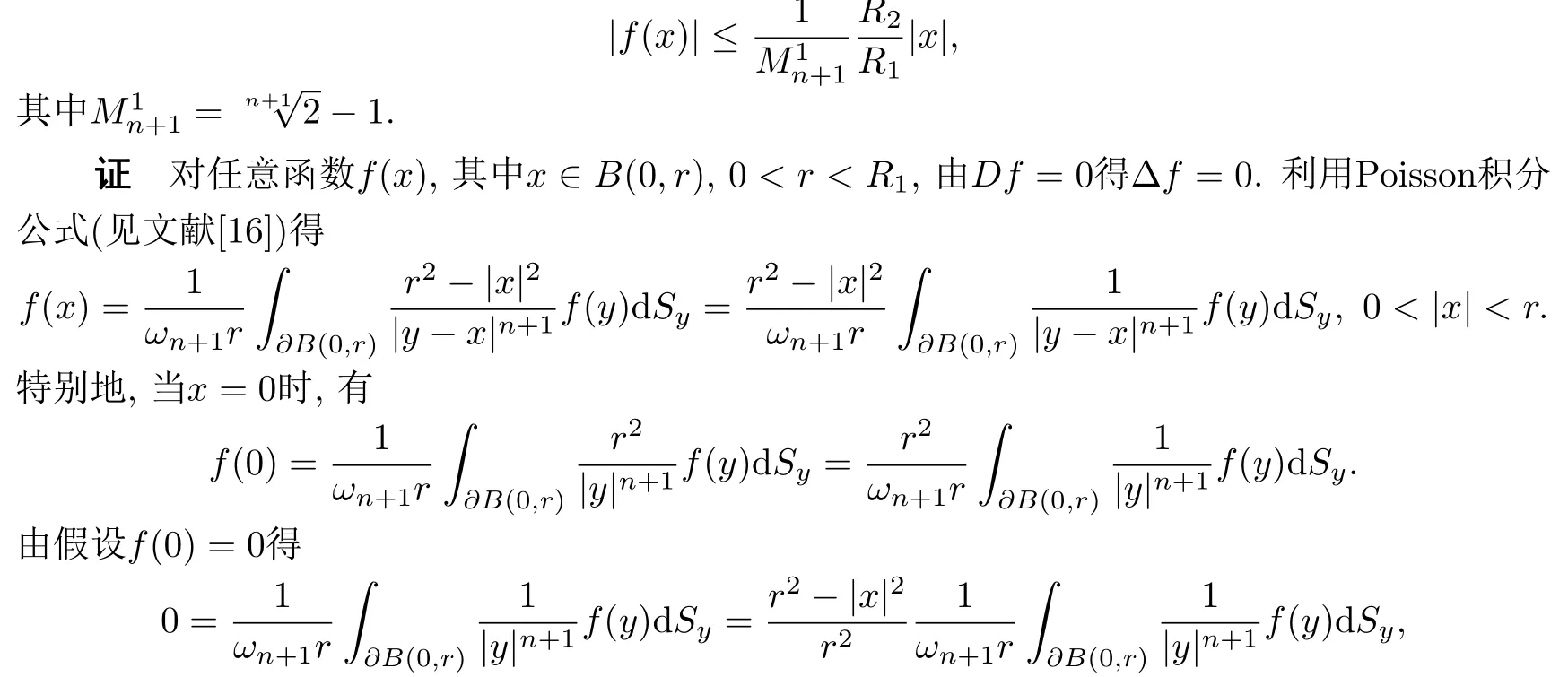
再利用假设对任意(0，R1)，有|f(x)|≤R2，对其变形得到

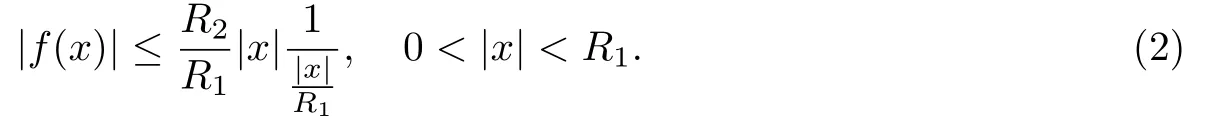
为方便比较(1)和(2)，令

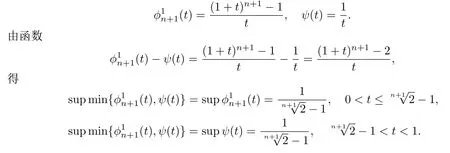
进一步

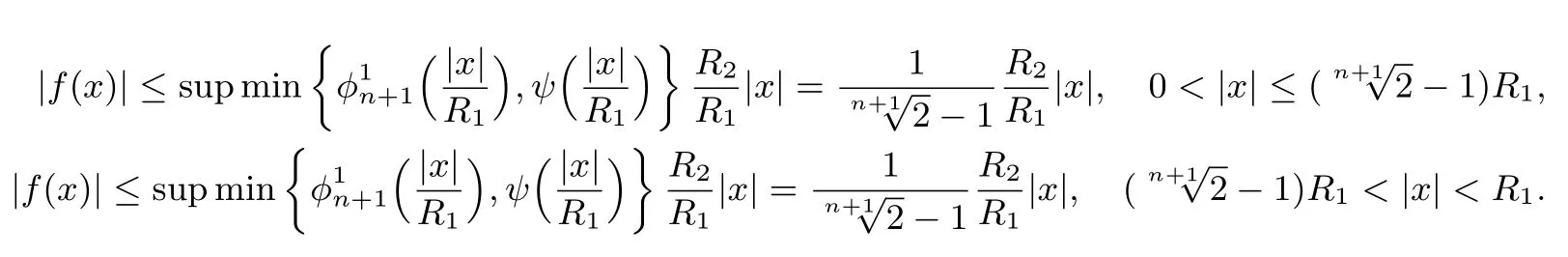
因此，对任意(0，R1)，有

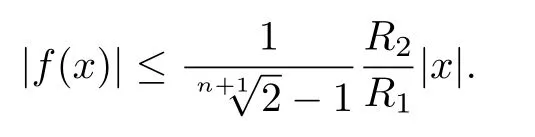
引理3.1对任意(0，r)和(0，r)，Cauchy核满足

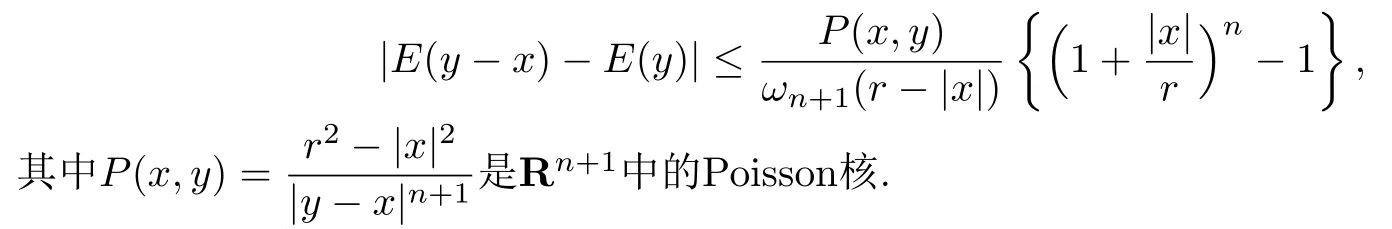
证由Cauchy核的定义，可知

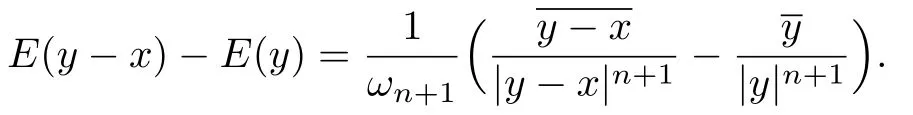
利用Hile引理(见文献[17]，p178)，得到

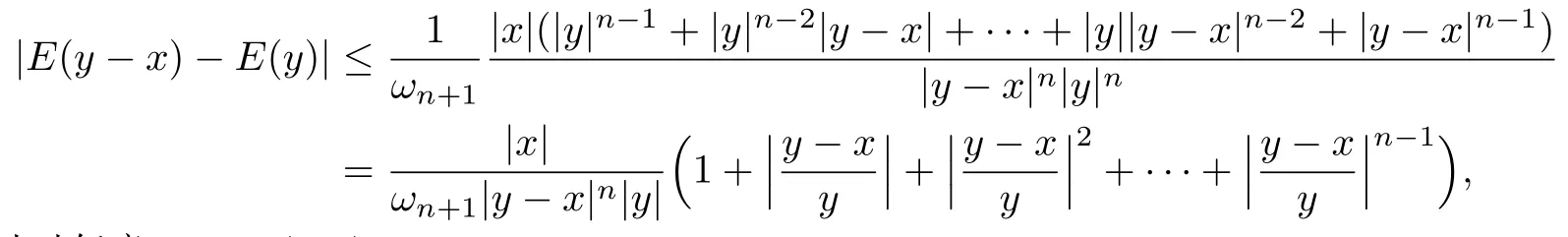
所以对任意(0，r)

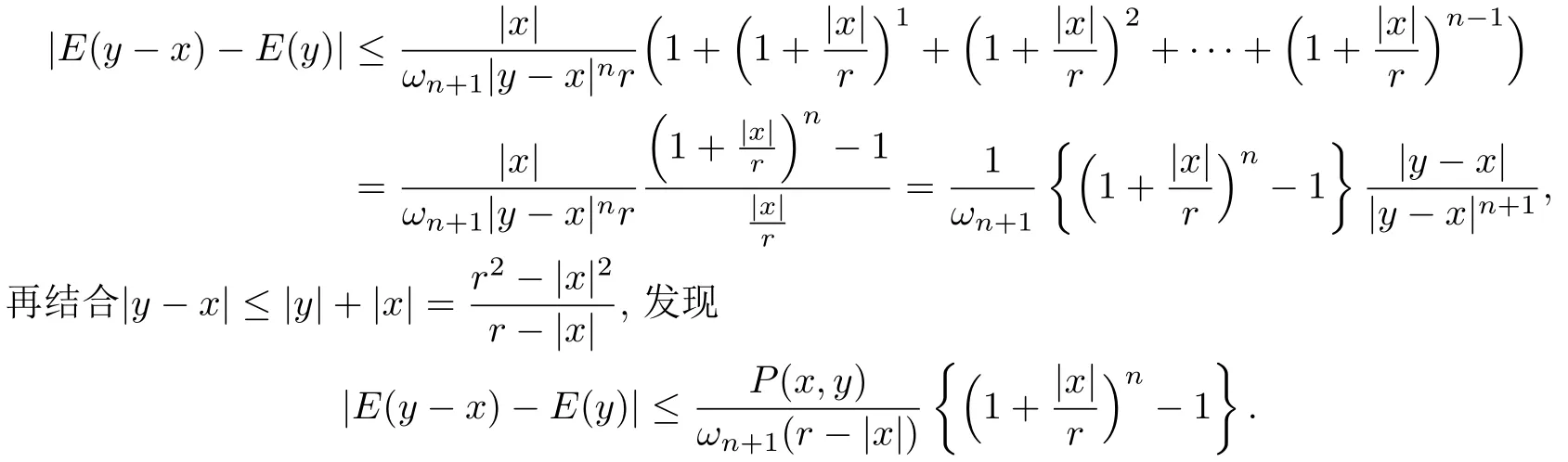
注该引理建立了Cauchy核和Poisson核之间的关系，为下文运用Cauchy积分公式建立带有精确常数的Schwarz引理做了铺垫.

定理3.2(Schwarz引理推广形式) 设B(0，R1)⊂Rn+1，函数1(B(0，R1)，Cl(n))满足

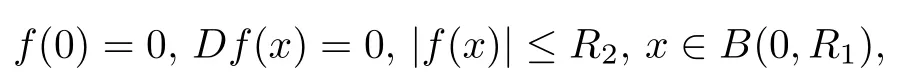
则对任意的(0，R1)，有

证第一步:证明存在(0，1)，使得对任意的(0，R1)，有

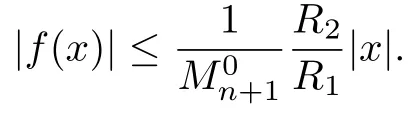
对任意左正则函数f(x)，其中(0，r)， 0＜r ＜R1，由Cauchy积分公式[10]，得

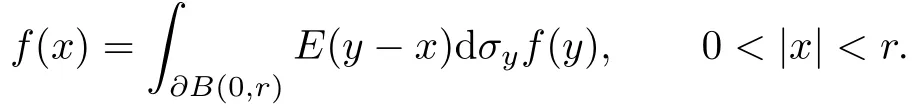
特别地，当x0时，有

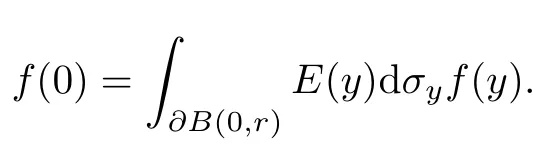
由已知f(0)0，可以推出

利用引理3.1中Cauchy核和Poisson核之间如下关系式

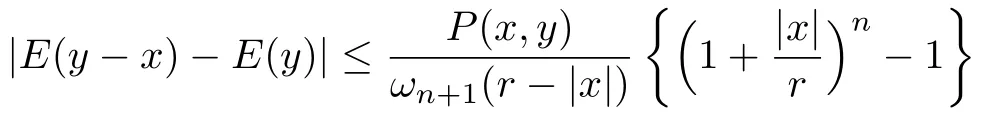
和文献[16]中公式

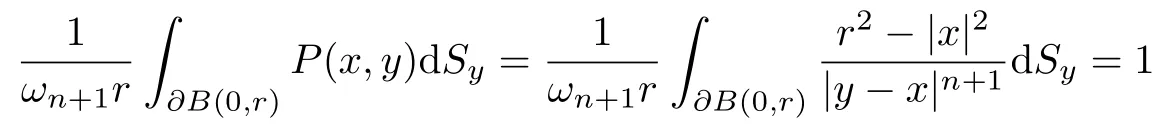
及本文中函数f(y)所满足的条件对任意(0，R1)，有|f(y)|≤R2，可以得到

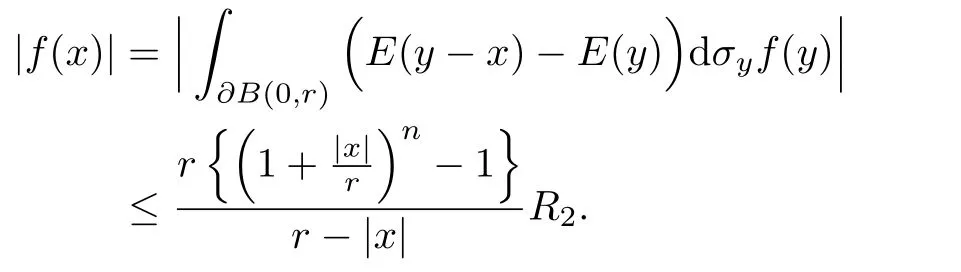
令r →则对任意0＜|x|＜R1，有

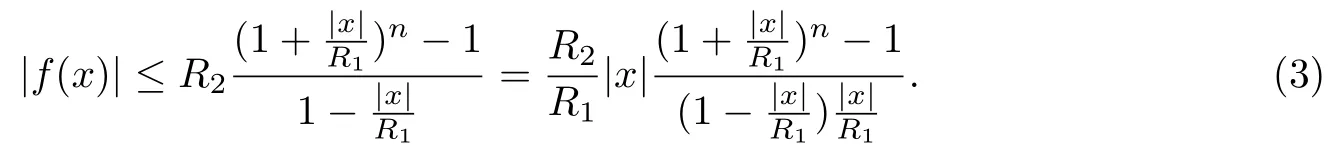
另外，可以将已知条件|f(x)|≤R2变形为

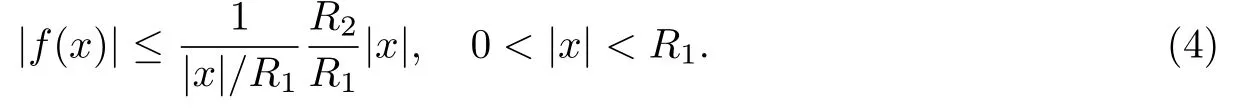
为分析(3)和(4)，令函数

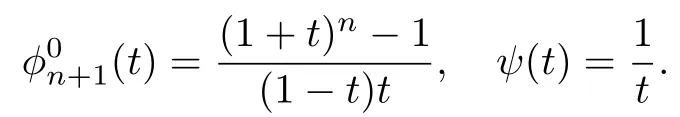
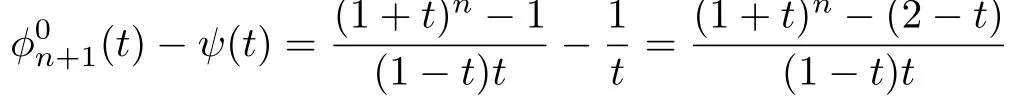
的分子g(t)(1+t)n -(2-t)在[0，1]连续，由零点定理及g(t)在(0，1)上为单射知存在唯一的(0，1)使得(1+t)n-(2-t)0，不妨记为t则

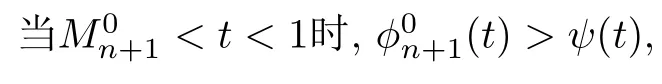
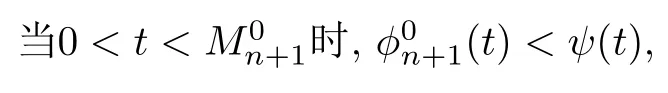
因而

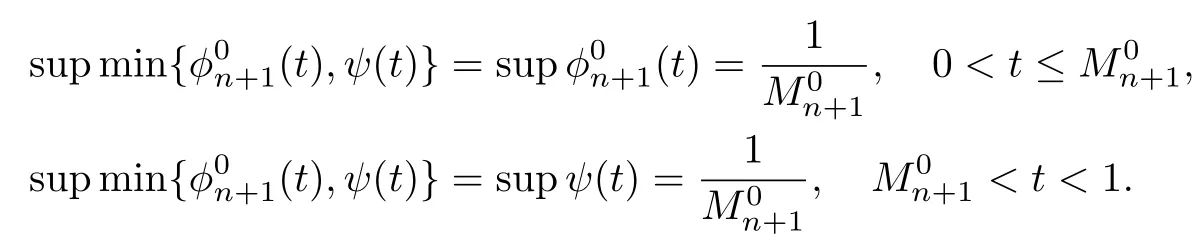
这意味着

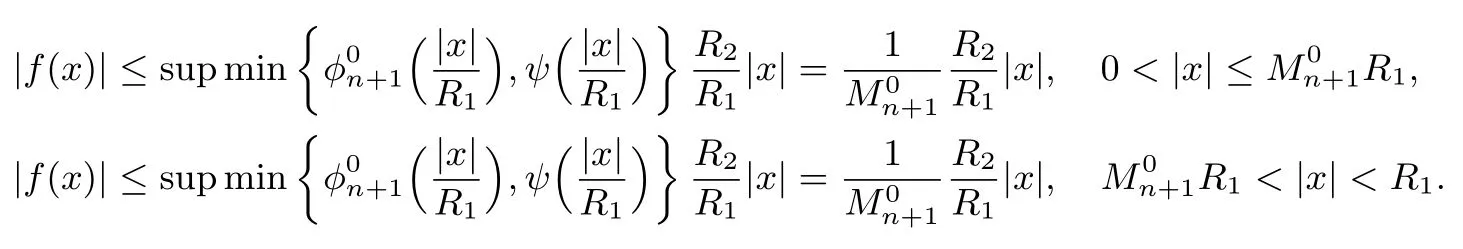
因此，对任意的(0，R1)，有

例为了直观地揭示定理3.2，首先从图上观察n2情形下，函数ψ(t)的大小关系.从图上可以看到

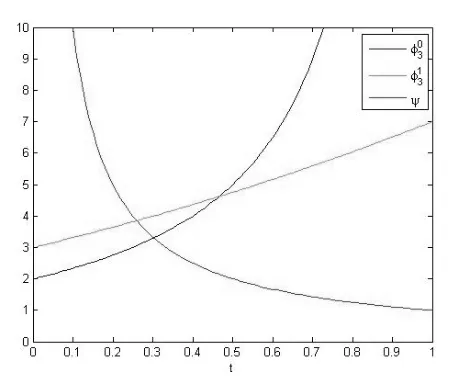
图3 和ψ

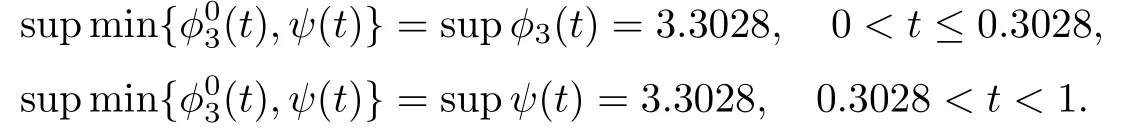
这意味着

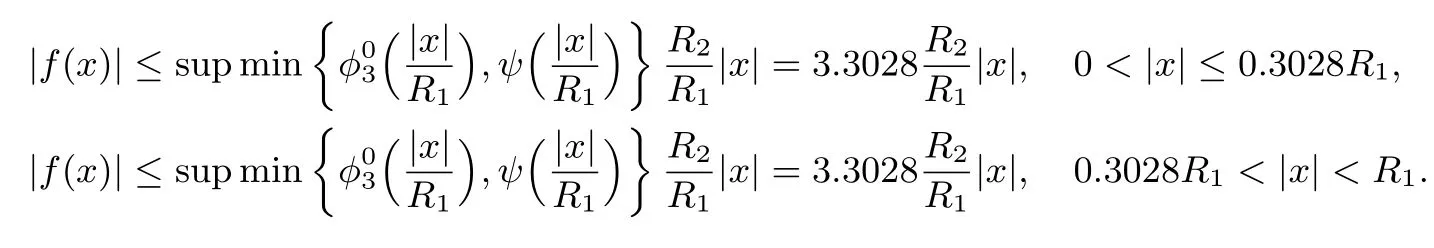
另外，从图2可以看到

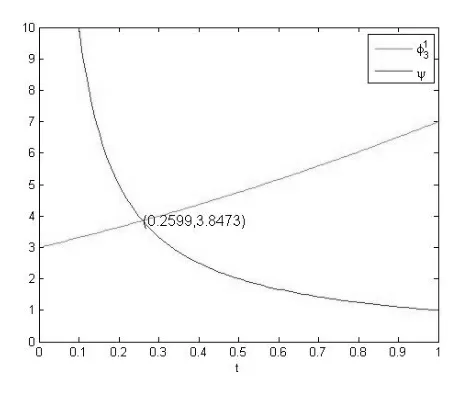
图2 和ψ

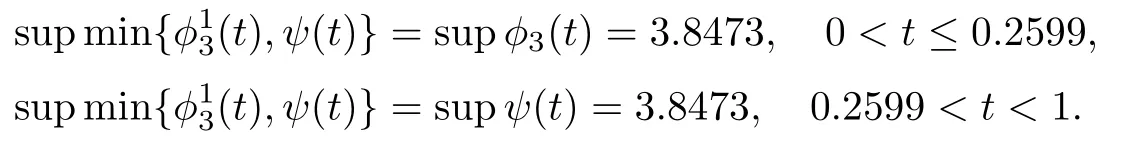
这意味着

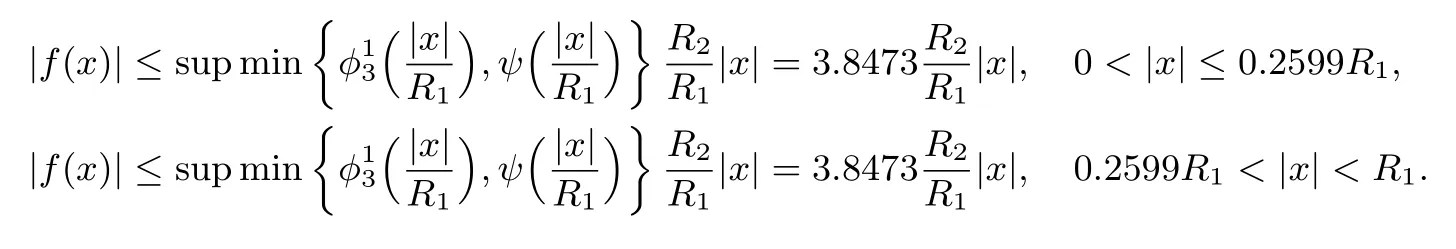
n3的情形如图4-6所示，不再过多解释.

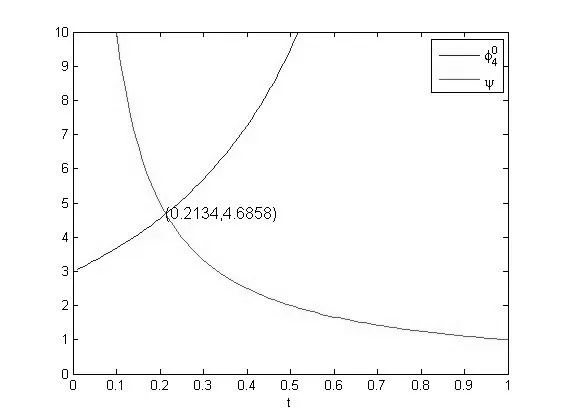
图4 和ψ

图5 和ψ

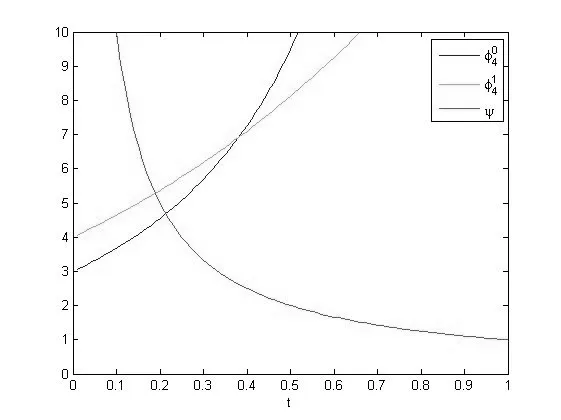
图6 和ψ

注从图1到6可以直观地看出，

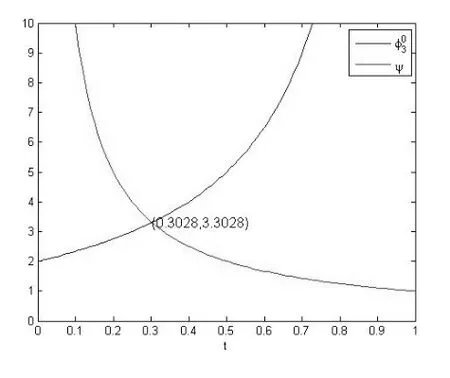
图1 和ψ

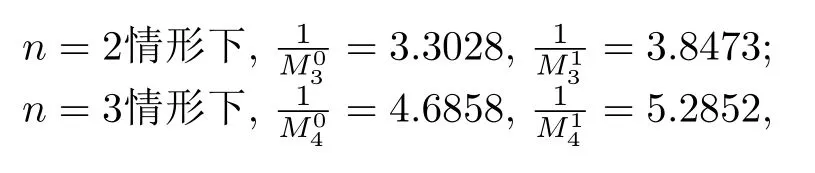
即基于Cauchy积分公式和Hile引理得到的常数要精确于基于Poisson积分公式得到的常数[6]，并该常数与R3中Helmholtz算子对应的结果相吻合[8].

作为一个特列，有以下结论

定理3.3(Schwarz引理) 设B(0，1)⊂Rn+1，函数1(B(0，1)，Cl(n))满足

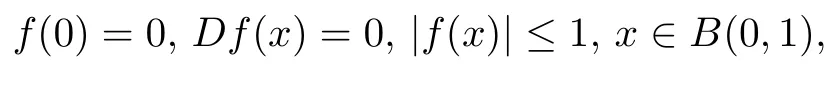
则对任意(0，1)，有