乌鲁木齐市新冠肺炎疫情数据的贝叶斯分析

古丽斯坦·库尔班尼牙孜田茂再

(1.新疆财经大学 统计与数据科学学院，新疆乌鲁木齐 830012;2.中国人民大学 应用统计科学研究中心，中国人民大学 统计学院，北京 100972)

§1 引言

新型冠状病毒肺炎(Corona Virus Disease 2019，COVID-19)，简称“新冠肺炎”，是一种由2019新型冠状病毒引起的急性呼吸道传染病.新冠肺炎出现以后持续蔓延至许多国家，严重威胁着人类的生命健康，因此引起了世界各国的广泛关注与高度重视.在全球抗击新冠肺炎的过程中，众多学者对疫情传播和发展趋势进行了大量研究.Guan和Hu[1]等收集截止2020年1月29日中国30个省，自治区，直辖市552家医院的1099例新冠肺炎确诊病例，对新冠肺炎的潜伏期，死亡率进行估计.刘勋，孟秋雨[2]等收集湖北省截至2020年2月10日新冠肺炎疫情数据，利用OpenGeoda软件对湖北省新冠肺炎发病的空间聚集性特征进行分析.周涛[3]等对我国COVID-19基本再生数值进行预测.白尧等[4]利用SEIAR模型对陕西省疫情风险进行了评估.

国家卫健委组织每天发布新冠肺炎每日新增确诊病例与每日新增无症状感染者病例，这为新冠肺炎的建模和分析提供了良好的基础.它们在描述疫情的传播特征，探讨疫情传播的影响因素，在数据驱动下预测疫情的可能发展趋势，评估防疫措施的有效性等方面起着重要作用.因此从理论层面探究这两组数据的分布特征，通过基于数学，统计学以及计算机科学的完整有效的分析方法来对数据进行建模，从样本入手挖掘出隐藏的，有价值的信息在新冠疫情分析中具有很重要的意义，并且对新冠疫情分析方法的重要补充.

目前国内外新冠疫情的有关研究主要集中在疫情发展趋势的预测[5-9]，疫情对经济[10]，旅游[11]等方面的影响与冲击等层面.利用贝叶斯方法探索疫情数据的分布特征方面的研究甚少.基于此，本文根据新疆乌鲁木齐市2020年7月15日至8月15日新冠肺炎疫情每日新增确诊病例与2020年7月15日至8月16日每日新增无症状感染者病例的实际数据，分别基于泊松分布，变点泊松分布与过度发散泊松分布建立统计模型，并利用贝叶斯方法对模型进行统计推断，旨在从理论层面揭示这两组数据的内在统计特征和统计规律，能为抗击疫情提供一定的理论依据.

统计推断中最常用的方法是古典统计与贝叶斯统计.其中古典统计是基于大样本推断总体，把未知参数看作一个未知的固定量，缺点是过于依赖样本信息，如果样本有偏或样本稀疏，则会使参数估计出现偏差.而贝叶斯统计是把未知参数也看作是随机变量，并充分利用先验信息，更加符合人类认知自然的过程.特别是对于小样本数据而言，基于大样本推断总体的传统统计模型受到更多挑战.而贝叶斯层次模型通过引入先验信息，充分考虑各种不确定性，可在一定程度上克服小样本缺陷[12-15].从数据自身的特征来看，新冠肺炎每日新增确诊病例与每日新增无症状感染者病例每天只有一个观测值，因此不满足大样本性质;再者每日新增确诊病例与每日新增无症状感染者病例也有可能不满足独立同分布假定.综上所述，直接利用古典统计方法，这两组数据可能会突破大样本与独立同分布的两个前提条件.而利用贝叶斯方法在理论上可能会更加严密可靠.因此为了突出贝叶斯方法在疫情数据分析中的重要作用，本文通过贝叶斯方法和分层贝叶斯方法对乌鲁木齐市每日新增确诊病例与每日新增无症状感染者病例进行分析.

本文的安排如下:§2分别基于泊松分布，变点泊松分布和过度发散泊松分布对乌鲁木齐市每日新增确诊病例与每日新增无症状感染者病例进行统计建模，并利用贝叶斯方法对模型进行统计推断;§3利用DIC值对三种模型的拟合优度进行评价;§4是本文的结论.

§2 乌鲁木齐市新冠肺炎数据的贝叶斯分析

本文研究的数据来源为2020年7月15日至2020年8月16日全国健康委员会公布的乌鲁木齐市每日新增确诊病例与每日新增无症状感染者病例数据.每日新增确诊病例的样本区间为7月5至8月15日，样本个数为n32;每日新增无症状感染者病例的样本区间为7月5至8月16日，样本个数为n33.样本期间乌鲁木齐市新冠肺炎每日新增确诊病例与无症状感染者病例变化趋势如下图1所示.下文对这两组数据的分布特征进行统计建模.

图1 每日新增确诊病例与无症状感染者病例的变化趋势图

2.1 基于泊松分布模型的贝叶斯分析

泊松分布是概率论中常用的一种离散型概率分布，适合于描述单位时间内随机事件发生的次数，如机器出现故障的次数;汽车站内候客人数;自然灾难发生的次数等.由于新冠肺炎每日新增确诊病例与每日新增无症状感染者病例是计数数据，且为离散随机变量，所以从数据的这个特点出发，先利用泊松分布进行建模.

2.1.1 基于泊松分布模型的每日新增确诊病例贝叶斯分析

假设乌鲁木齐市总人口为N(N355.2万人)，每日新增确诊病例发病率为p1，每日新增确诊病例Y1，···，Yn是独立同分布的离散随机变量，且Yi服从二项分布b(N，p1).因为N很大，p1很小，根据泊松定理[16]，随机变量Yi的分布可以用参数为λNp1的泊松分布来近似，即

其中λ代表每日平均新增确诊病例.

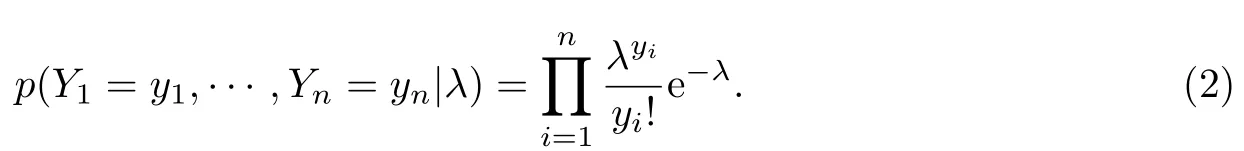
为了获取参数λ的后验分布，需要先给定相应的先验分布.根据国内外研究经验，λ的先验分布假定为伽马分布，即π(λ)Ga(α，β).样本的联合分布函数和π(λ)相乘可以得到联合后验分布

因此每日平均新增确诊病例λ的条件后验分布为

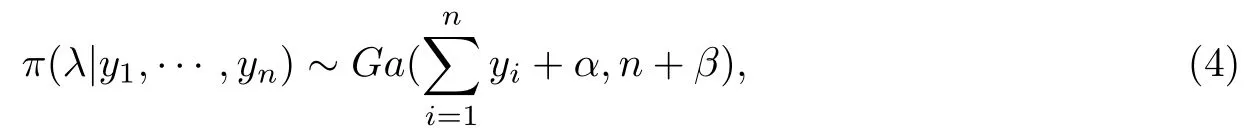
其中Ga(·)代表伽马分布.基于参数λ的条件后验分布，本文采用MCMC方法来对后验分布进行抽样.MCMC算法的基本思想是:通过从后验分布中获取随机样本，建立一条平稳分布为后验分布的马尔科夫链，然后根据这些样本对未知参数进行统计推断.MCMC算法中常用的抽样方法有Metropolis-Hasting算法，Gibbs算法，独立抽样算法等.其中最简单，应用最广泛的MCMC方法是Gibbs算法.当参数的后验分布为标准分布时，Gibbs算法直接从参数的后验分布中抽取样本[17].根据(4)式可知，参数λ的后验分布为常见的伽马分布，所以可以用Gibbs抽样方法直接对验分布进行抽样.本文利用Winbugs软件进行操作[18].假定参数λ的的初始值为10，超参数α4，β2，马尔科夫迭代链长度为10000.表1给出了参数估计的最终结果，图2是MCMC方法数据模拟得到的参数λ的轨迹图，核密度图和自相关函数图.

表1 每日平均新增确诊病例的贝叶斯估计

从表1可以看出，每日平均新增确诊病例的贝叶斯估计25.21，跟实际值25.93比较接近，参数估计的MC误差趋向于零，说明用模型的拟合效果较好.由图2可以看出，抽样值基本都均值附近波动，核密度估计图近似正态，自相关函数值趋近于零，说明产生的马尔科夫链呈现收敛状态，根据λ与p1的关系计算出来的样本期间新增确诊病例平均发病率p1的估计值为2.2436×10-4，这跟实际发病率p12.2375×10-4的比较接近.总之，模型来拟合每日新增确诊病例比较合理.

图2 参数λ的迭代轨迹，核密度与自相关函数图

2.1.2 基于泊松分布模型的每日新增无症状感染者病例贝叶斯分析

同理，假设样本期间乌鲁木齐市新增无症状感染者发病率为p1′，平均新增无症状感染者病例为ηNp1′.每日新增无症状感染者病例Z1，···，Zm服从参数为η的泊松分布，即

其中z(z1，···，zm)是每日新增确诊病例的样本观测值.设η的先验分布为伽马分布Ga(α1，β1).得到的每日平均新增无症状感染者病例η条件后验分布为

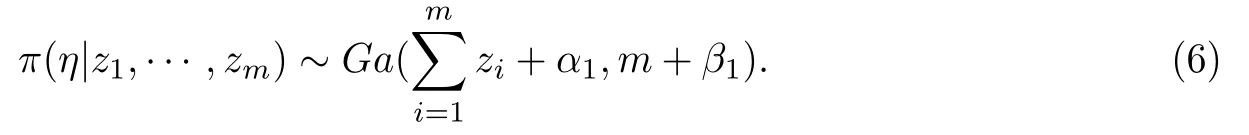
利用Gibbs算法对η的后验分布进行抽样，初始值取为η5，超参数设定为α2，β2.表2给出了η的最终参数估计结果，图3是MCMC方法数据模拟下得到参数η的迭代轨迹图，核密度图与自相关函数图.

表2 η的贝叶斯估计结果

图3 参数η 的迭代轨迹，核密度与自相关函数图

从表2的结果可以看出，每日平均新增无症状感染者病例η的贝叶斯估计为11.24，估计结果跟样本均值11.51非常接近，参数估计的MC误差趋向于零，说明模型的拟合效果很好.由图3可以看出，参数η的迭代轨迹基本稳定，核密度估计图近似正态，自相关函数值趋近于零，因此可以认为迭代已经收敛.根据η与p1′的关系得到的每日新增无症状感染者平均发病率的估计为1.0250×10-4，这跟无症状感染者实际发病率p1′1.0839×10-4很接近，因此利用贝叶斯方法估计模型参数是有效的.

2.2 基于变点泊松分布模型的贝叶斯分析

在上文的建模过程中假定每日新增确诊病例和每日新增无症状感染者病例在整个样本期间是同分布的，但实际数据有可能不满足这个假定.为了更深入地探究数据的分布特征，本节利用变点泊松分布对数据进行建模.在变点模型中先把样本按照出现时间的先后顺序排列，如果在某个未知的时刻开始样本的数字特征和分布特征突变，那这个未知的时刻称为变点.变点检测分为对分布参数的变点检测和分布本身的变点检测[19].本文基于分布参数的变点检测方法，只有存在一个变点的情形下分别对两组数据进行建模.

2.2.1 基于变点泊松分布模型的每日新增确诊病例贝叶斯分析

假设τ是每日新增确诊病例的一个变点，新增确诊病例的发病率为p2，每日新增确诊病例Yi服从参数为λNp2的泊松分布.模型的第二层对λ进行建模.假设，当i1，···，τ时，λexp(β1);当iτ+1，···，n时λexp(β1+β2).把这两个模型结合可以写成

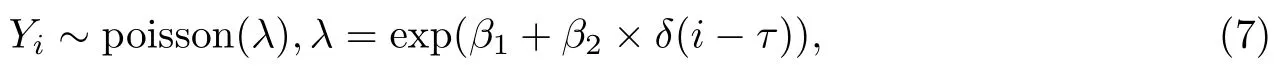
其中δ()是示性函数，若()里的表达式为非负其值为1，否则为零.参数β1与β2的先验分布设定为独立先验，并假定为π(βk)～ N(0，0.001)(k1，2).假定变点发生在样本出现的时间间隔内，变点参数τ的先验分布为U(1，n)，n32.利用MCMC方法对未知参数β1，β2和τ进行贝叶斯推断，进行10000次迭代，参数初始值的设定为τ5，(β1，β2)(0，0)，表3列出了得到的参数估计结果.图4，图5给出了参数β1，β2和τ的迭代轨迹图核密度估计图.

表3 每日新增确诊病例变点泊松模型参数的估计结果

图4 参数β1，β2与τ的迭代轨迹图

图5 参数β1，β2与τ的核密度图

2.2.2 基于变点泊松分布模型的每日新增无症状感染者病例贝叶斯分析

同理，假设τ1是每日新增无症状感染者病例的一个变点，每日新增无症状感染者病例zj～poisson(η)(j1，···，m).假定当j1，···，τ1时，ηexp(γ1).当jτ1+1，···，m时ηexp(γ1+γ2).因此有

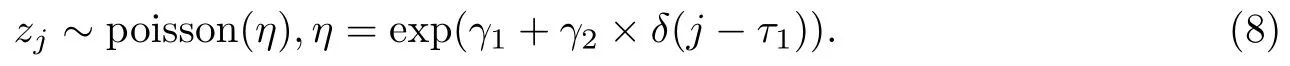
其中δ()是示性函数，若()里的表达式为非负其值为1，否则为零.假定γ1与γ2的先验分布互相独立，并假定为π(γk)～ N(0，0.001)(k1，2)，变点参数τ1的先验分布为U(1，m)，m33.利用MCMC方法对未知参数进行贝叶斯推断，进行10000次迭代.参数初始值的设定为(γ1，γ2)(0，0)，τ15.最终得到的参数估计结果如下表4所示.

表4 每日新增无症状病例变点泊松模型的估计结果

图6 参数γ1，γ2 与τ1的迭代轨迹图

从表4的结果可以发现，的置信区间不包括零，说明是显著不为零，意味着15.5是每日新增无症状感染者病例的一个变点.的符号是负的，可以认为开始每日新增无症状感染者病例开始减少.根据以上结果计算可得，7月15日至29日，每日平均新增无症状感染者的贝叶斯估计为e2.85117.305，发病率的估计为7.4083×10-5，这跟样本均值η17.333 和实际发病率为p′7.4162×10-5非常接近.7月30日到8月16日每日平均新增无症状感染者的贝叶斯估计为e(2.851-0.958)6.6392，实际值为η6.6667，发病率的估计为3.4122×10-5，实际发病率为p′3.4229×10-5，可见模型的估计效果很好.参数估计的迭代轨迹图和核密度图分别在如下图7，图8所示.由图7，图8可以看出，当迭代次数到达一定数量后参数γ1，γ2与τ1的抽样值基本都在均值附近波动，可以认为产生的链具有较好的收敛性.从核密度估计来看γ1，γ2的核密度基本正态，变点参数τ1的核密度大致可以看成均匀分布，说明参数的先验分布均为共轭先验分布.

图7 参数γ1，γ2与τ1的核密度图

2.3 基于过度发散泊松分布模型的贝叶斯分析

由实际样本数据计算可得，样本期间乌鲁木齐市新冠肺炎每日新增确诊病例的均值为E(y)25.937，方差为Var(y)717.546;每日新增无症状感染者病例的均值为E(Z)11.515，方差Var(Z)97.695，显然这两组数据的均值与方差不相等，不满足泊松分布的均值与方差相等的特征，因此这两组数据可以认为过度发散数据[20].本节基于过度发散泊松分布对这两组数据进行建模.

2.3.1 基于过度发散泊松分布模型的每日新增确诊病例贝叶斯分析

假设每日新增确诊病例的发病率为pi，每日新增确诊病例Yi(i1，···，n)服从参数为λiNpi的泊松分布，具体为

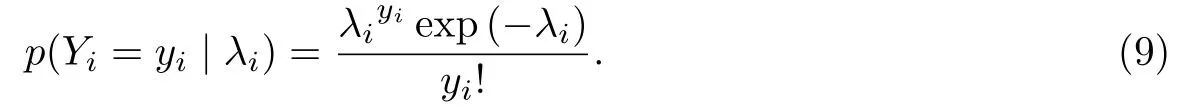
分层模型的第二层对λi进行建模，假定λi服从形状参数为α，尺度参数为β的伽马分布.即

其中α，β为超参数，分层模型的第三层假定α的先验分布为指数分布，β的先验分布为伽马分布.具体而言

其中A，B，C为确定的常数.令y(y1，···，yn)，λ(λ1，···，λn)，把参数先验分布乘以似然函数，可以得到联合后验分布为:

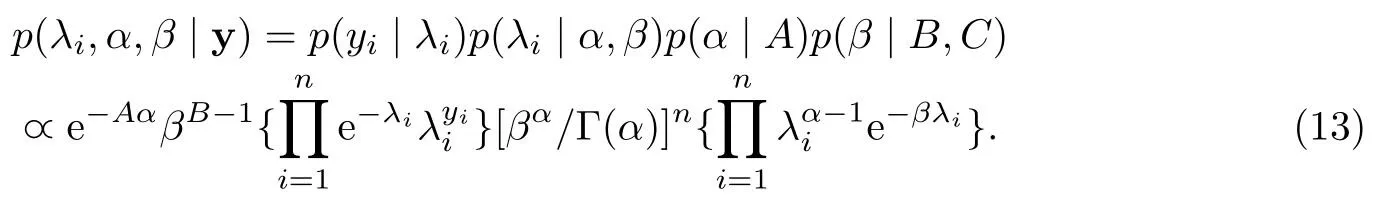
从以上的联合后验密度函数可以推出，λi，β和α的条件后验分布分别为

可见参数λ与β的后验分布均有标准的分布形式，直接可以用Gibbs算法进行抽样，但参数α的后验分布没有标准的分布形式，需要采用MH 算法进行抽样，因此本文采用Gibbs抽样和MH算法相结合的MCMC方法[21-22]估计模型的未知参数θ(λ，α，β).MH算法抽样过程中所需要的提议分布选取为0到1上的均匀分布U(0，1).通过抽样产生的序列(θ(0)，θ(1))，···，θ(k)是一个马尔科夫链，它的平稳分布收敛于联合后验密度p(θ|y)[20].抽样次数设定为N10000，未知参数的初始值设定为λi(0)5(i1，···，32)，(α(0)，β(0))(2，1)，超参数设定为A2，B2，C1.表5给出了最终得到的参数估计结果.因为篇幅有限，下面的图8，图9只给出了λ的最大分量λ16与超参数α，β对应的迭代轨迹图和核密度估计图.

表5的结果表明，每日平均新增确诊病例λi(i1，···，n)的估计值与实际值非常接近，标准差也比较小，参数估计的MC误差趋向于零，利用贝叶斯方法对模型估计是有效的.由图8，图9可以发现，当迭代次数到达一定数量后参数α，β和λ16的迭代轨迹基本稳定，可以认为所产生的马尔科夫链收敛.对于核密度而言，λi(i1，···，32)的核密度近似为正态分布，参数α和β的核密度近似可以看成伽马分布，这说明参数β的先验分布是共轭先验分布.

图8 参数λ16，α与β的迭代轨迹图

图9 参数λ16，α与β的核密度图

表5 每日平均新增确诊病例的贝叶斯估计结果

2.3.2 基于过度发散泊松分布模型的每日新增无症状感染者病例贝叶斯分析

假设乌鲁木齐市7月15日至8月16日每日新增无症状感染者病例发病率为pj(j1，···，m)，每日新增无症状感染者病例zj(j1，...，m)服从参数为ηjNpj的泊松分布，取ηi的先验分布为Ga(α2，β2)，超参数α2的先验分布为exp(A1)，β2的先验分布为Ga(B1，C1)，A1，B1，C1为给定的常数.记η(η1，...，ηm)，通过跟上文一样的思路与步骤，利用MCMC方法对未知参数(η，α2，β2)进行估计，总共进行N10000 次迭代，未知参数的初始值设定为ηj(0)8(j1，···，m)，(α2(0)，β2(0))(2，1)，常数A13，B12，C12.最终得到的参数估计结果如下表6所示.因为篇幅有限，图10，图11中只给出了η的最大分量η11与超参数α2，β2对应的迭代轨迹图，核密度图.表6中的参数估计结果表明，每日新增无症状感染者ηj(j1，···，m)与发病率pj的估计值跟实际值很接近;估计量的MC 误差趋近于零，因此可以认为模型对实际数据的拟合效果很好.由图10，图11可以看出，当迭代次数到达一定数量后参数η11与α2与β2的迭代轨迹基本稳定，所产生的的马尔科夫链收敛.参数η11的核密度近似正态，α2和β2核密度近似为伽马分布，β2的先验分布是共轭先验分布.

图10 参数η11，α2与β2的迭代轨迹图

图11 参数η11，α2与β2的核密度图

§3 模型的评价

由上文的结果可以看出，对于每日新增确诊病例和每日新增无症状感染者病例而言，三个模型均有较好的拟合效果，为了选择其中的最优模型，利用Spiegelhalter等[23]提出的DIC准则来对三种模型的拟合优度进行评价.DIC(Spiegelhalter[23])是Akaike信息标准(AIC)在贝叶斯统计方面的推广.它的具体形式为

表7 各个模型的DIC值计算结果

由表7的结果可知，对于乌鲁木齐新冠肺炎每日新增确诊病例与每日新增无症状感染者病例而言，基于过度发散泊松分布模型的DIC值最小，其次为变点泊松模型，泊松模型的DIC值最大，这说明过度发散泊松分布模型能够为最准确地刻画出这两组数据的分布特征，因此对这两组数据利用过度发散泊松分布来建模是最合理的.

§4 结论

每日新增确诊病例和每日新增无症状感染者病例对新冠肺炎传播过程的描述，分析和探讨疫情传播的影响因素方面重要作用，并且为新冠肺炎的建模和分析提供了良好的基础.因此本文从乌鲁木齐市新冠肺炎疫情每日新增确诊病例与无症状感染者病例的实际数据出发，以探索数据的分布特征为目的，分别基于泊松分布，变点泊松分布，过度发散泊松分布对数据进行统计建模，利用贝叶斯方法估计模型中的未知参数，并利用DIC值对模型的拟合优度进行评价.结果表明，三种建模方法对两组数据都具有较好的适用性，相比之下，基于过度发散泊松分布的模型在拟合优度方面均优于其它两个模型，因此对这两组数据利用过度发散泊松分布来进行建模是最为合理的，其次为基于变点泊松分布的模型，泊松分布模型的拟合优度相对较差.