分数维下基于分数阶导数模型的期权定价

宋丽娜，朱 荻

(东北财经大学 数据科学与人工智能学院，辽宁大连 116025)

§1 引言

期权是一种活跃在国内外金融市场的衍生产品之一.我国内地市场上证50ETF期权和沪深300ETF期权分别于2015年2月9日和2019年12月23日上市交易.内地期权市场的扩容，一方面丰富了金融市场，有利于吸引大量资金进场;另一方面应该认识到风险管理的紧迫性和重要性.充分发挥期权双刃剑作用的关键是对其合理定价.经典的期权定价方法包括Black-Scholes模型[1-5]，二叉树模型[6]和倒向随机微分方程[7]等.其中，Black-Scholes模型的问世为研究者提供一种思路，利用偏微分方程的理论和方法研究期权定价问题.随着研究工作的发展，[8]引入Schrödinger型非线性偏微分方程替换线性Black-Scholes方程作为期权定价模型.针对这一模型，[9]首次提出金融畸形波解，成功刻画金融市场中资产价格波动的怪波现象.经典模型的改进和完善一直以来都是专家学者的重点研究工作.归因于大量实证研究发现:金融资产价格变动存在长记忆性.[10-15]利用分数Browain运动取代标准Browain运动建立分数次Black-Scholes模型在分形市场下定价期权.

分数阶偏微分方程是对整数阶偏微分方程的统一和推广，分数阶导数算子是一个积分-微分算子，能够有效地刻画事物发展的历史依赖性，是分形几何和分形动力学建模的有效工具.分数阶偏微分方程已被引入定价理论.目前所涉及的模型可分为三类，一是时间分数阶偏微分方程，[16]在修正的Riemann-Liouville分数阶导数定义下给出时间分数阶Black-Scholes方程.二是空间分数阶偏微分方程.[17]在三种特殊的L´evy过程FMLS，CGMY和KoBoL下推导出金融市场中带有Riemann-Liouville分数阶导数的扩散方程.[18-21]对上述两种分数阶期权定价模型进行解法研究.第三是时空分数阶偏微分方程.在修正的Riemann-Liouville分数阶导数下，[16]给出带有一个分数阶参数的Black-Scholes方程，[22]得到双参数的分数阶Black-Scholes模型.之后，[23]给出带有交易费的时空分数阶导数模型，并利用中国内地市场的上证50ETF期权说明结果的有效性.[24]采用Caputo和Riesz-Feller分数阶导数利用Green函数推导分数阶扩散方程定价欧式期权并且利用Mellin-Barnes积分表达式给出定价公式.在Caputo导数下，朱元国等将分数阶不确定微分方程引入期权定价模型[25-26].

分数阶微积分和分数阶偏微分方程在期权定价问题中的应用在近几年得到快速发展，但是不可否认，众多问题有待进一步解决，诸多方面有待进一步完善和提高.新型定价模型和定价方法仍然是学术研究者和市场参与者关注的重点.随着分数阶微积分的发展，分数阶导数的定义有多种形式，例如，分数阶Riesz导数，Grünwald-Letnikov分数阶导数，Riemann-Liouville分数阶导数和Caputo分数阶导数等.其中，Caputo分数阶导数是对Grünwald-Letnikov导数定义的扩展.在此定义下，常数的导数等于零并且进行Laplace变换时对初值条件的要求与整数阶微积分一致.鉴于此，Caputo分数阶导数被广泛地应用于物理，力学和工程等研究领域.与已有模型不同，本工作依据金融市场的分形特征利用对冲技术建立带有Caputo型导数的分数阶期权定价模型.本文余下安排如下:§2推导出时空分数阶期权定价方程;§3利用改进的求解技术获得分数阶导数模型的半解析解;§4将所得结果引入中国内地期权市场，利用数据对分数阶导数模型进行解释;最后，§5给出结论和讨论.

§2 分数阶导数期权定价方程

在本文的工作中，采用对冲组合建立分数阶导数期权定价模型，故对市场作以下假设.

I 对冲组合Πt在时间段[t，t+dt]的价格变化满足下面等式

其中St表示标的资产的价格.

II 标的资产价格的变化遵循下列分数次指数方程

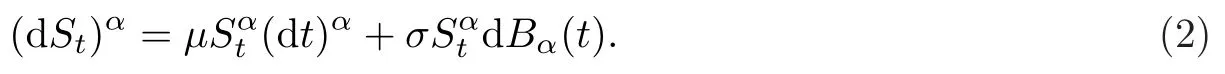
其中μ，σ分别表示期望回报率和标的物的波动率.Bα(t)表示带有Hurst指数α的分数Brownian运动.方程(2)的形式来自文献[22].

III 在分数阶导数下，设有E(dΠt)rΠt(dt)α.

α作为Caputo型分数阶导数的阶数，有如下定义.

定义2.1[27]在Caputo分数阶导数定义下，函数f(x)的α阶导数定义为

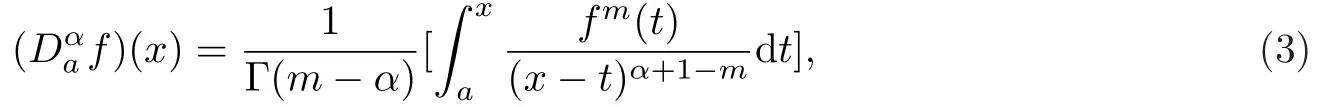
其中m-1(x)

方程(1)的设计源于Caputo分数阶导数定义下的广义中值定理.

引理2.2[28]设f(x)[a，b]，(a，b]，且0＜α ≤1，那么有

其中(a，b].

根据分数阶微积分，分数阶偏微分方程和期权定价理论，得到以下结论.

定理2.3基于假设I -III，期权价格V(S，τ)满足下列时空分数阶偏微分方程，

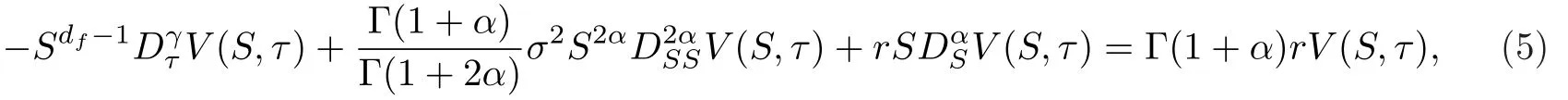
其中df是分形维数.τT -t，T表示期权的到期日.

证首先，建立对冲组合

基于假设I，对冲组合(6)在时间段[t，t+dt]的价值变化是

为实现Caputo分数阶导数建模，本工作假设定价模型有一个变量可分离函数解V(S，t)，即

回顾Caputo分数阶导数定义下的广义Taylor级数展开式.

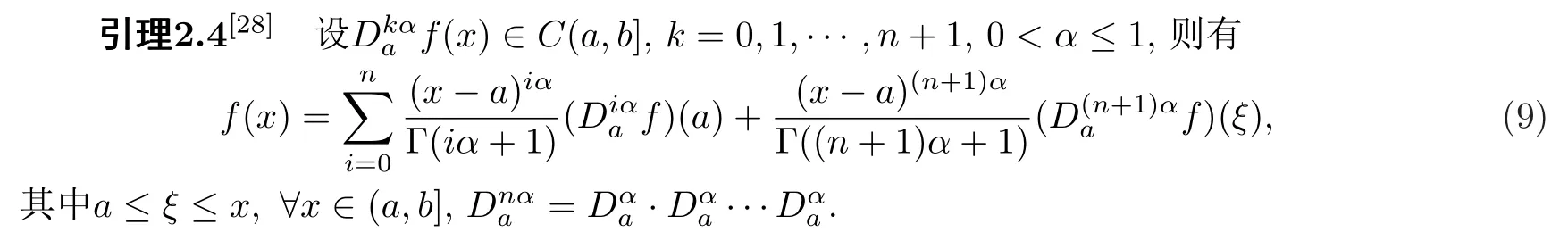
利用广义Taylor公式(9)，将V1(S)和V2(t)展成带有相同阶数α的广义Taylor级数，则有

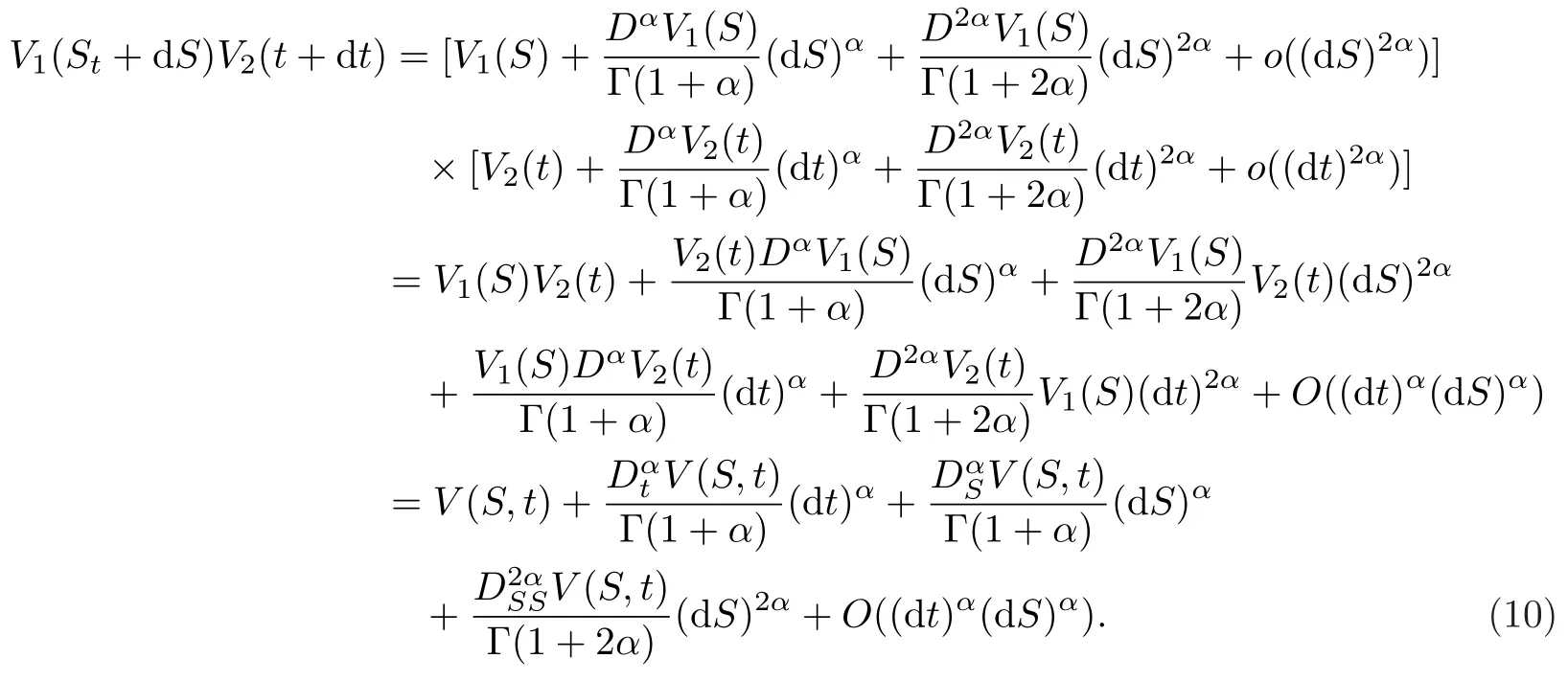
将表达式(11)代入方程(7)中，并令

可以得到下面表达式

借助于假设III，本工作建立如下形式的分数阶偏微分方程，

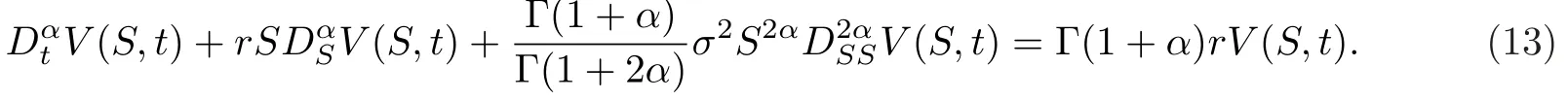
利用[29-30]，文献[22]建议将金融市场的期权价值变化作为一种分形传输系统，为此设期权价格与总流通率满足下列方程

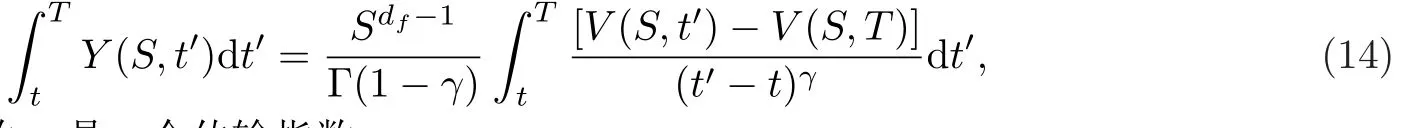
其中df是分形维数，γ是一个传输指数.

这里将股票市场作为分形介质，Y(S，t)有表达式

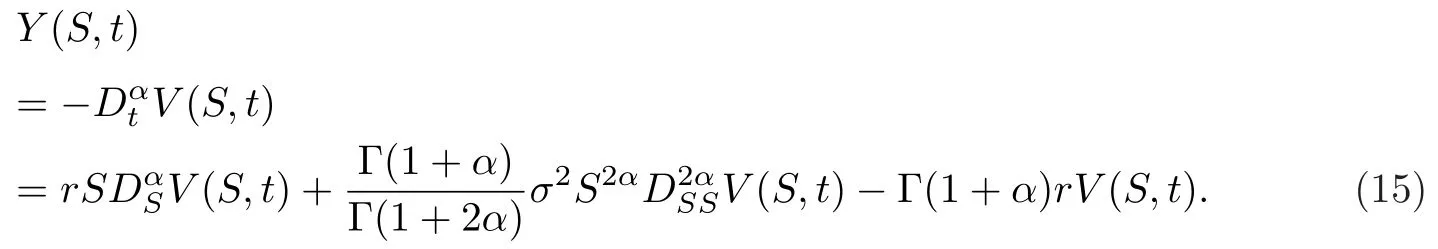
最终可以建立时空分数阶偏微分方程

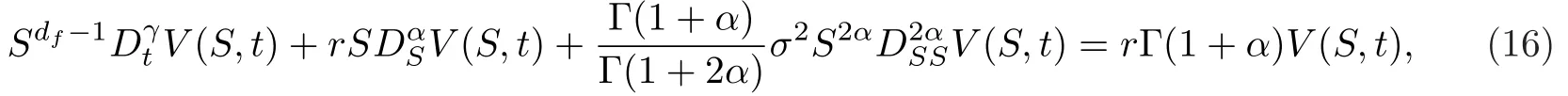
其中

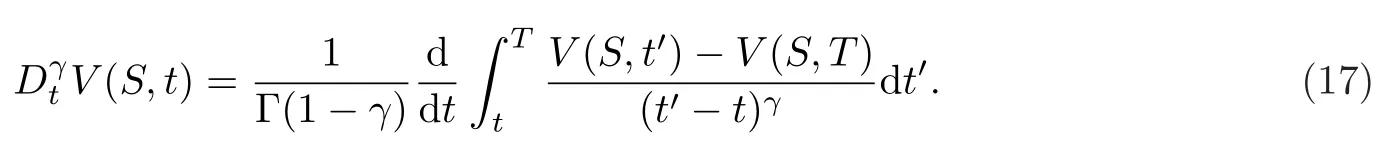
进一步作变量代换

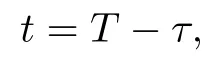
得到

方程(18)的最右端是一个修正的Riemann-Liouville分数阶导数.正如文献[16]指出:当函数是可微的，修正的Riemann-Liouville分数阶导数定义下产生的结果与Caputo导数定义产生的是一致的.文献[31]也给出等价关系证明.所以，本工作直接采用Caputo分数阶导数定义下的方程(5)，连同初边值条件，建立时空分数阶导数期权定价模型，定价标准的欧式和美式期权.

§3 优化的半解析解

本节研究期权价格V(S，τ)满足方程(5)和下列初边值条件组成的初边值问题，

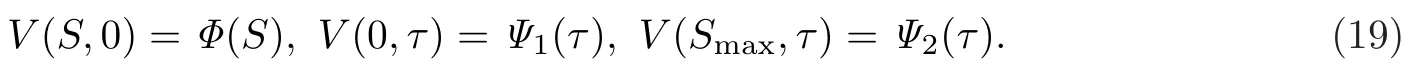
首先利用变量代换

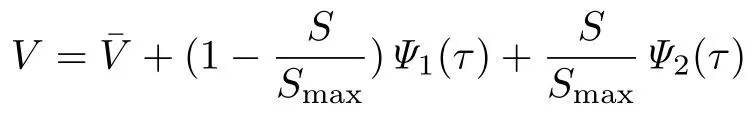
使边界条件齐次化，方程(5)转化为

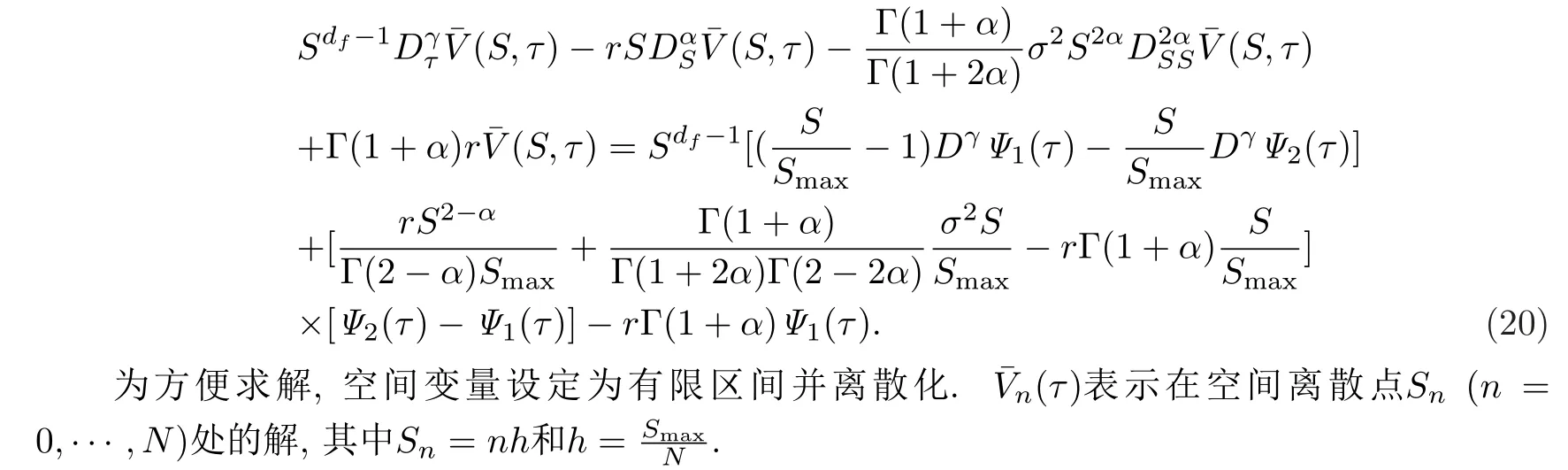
根据Caputo型导数的L算法[32]，采用下面分数阶微商的近似公式

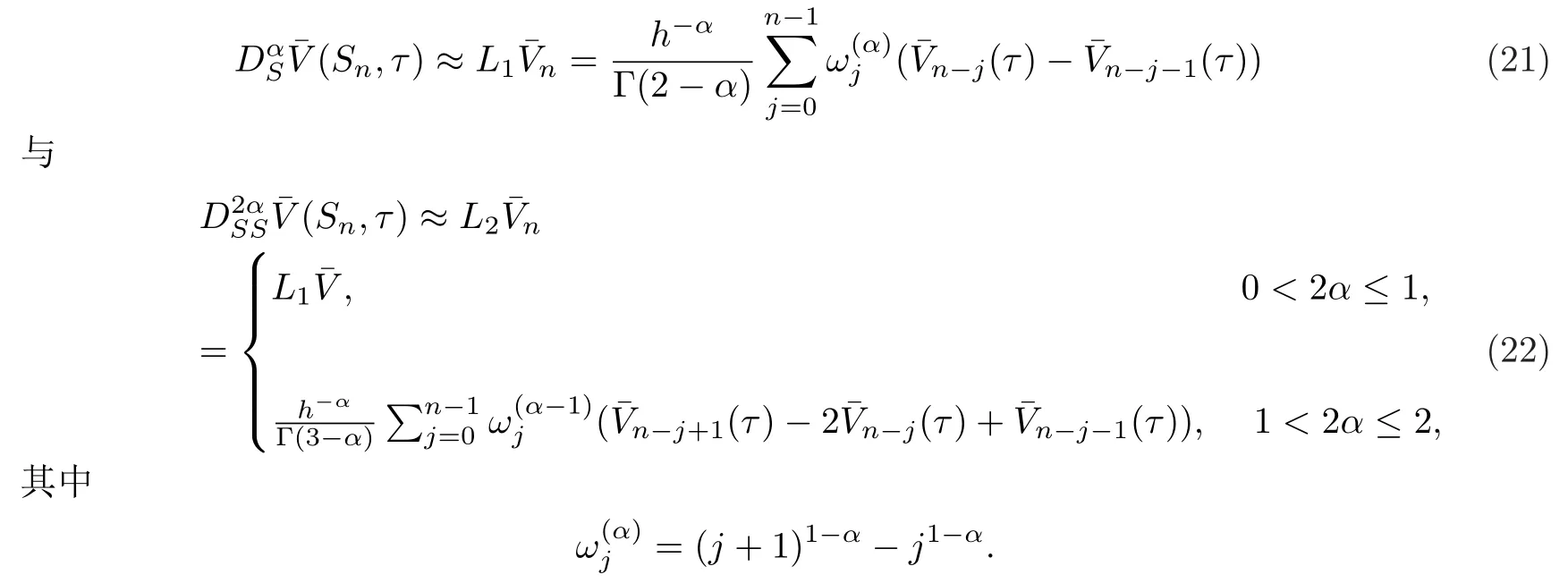
由于经典的Black-Scholes方程含有二阶偏导数，为接近这一点，在下面的计算过程中，考虑1＜2α ≤2.

在空间点Sn上，利用优化方法求解方程.为此改写方程(20)为

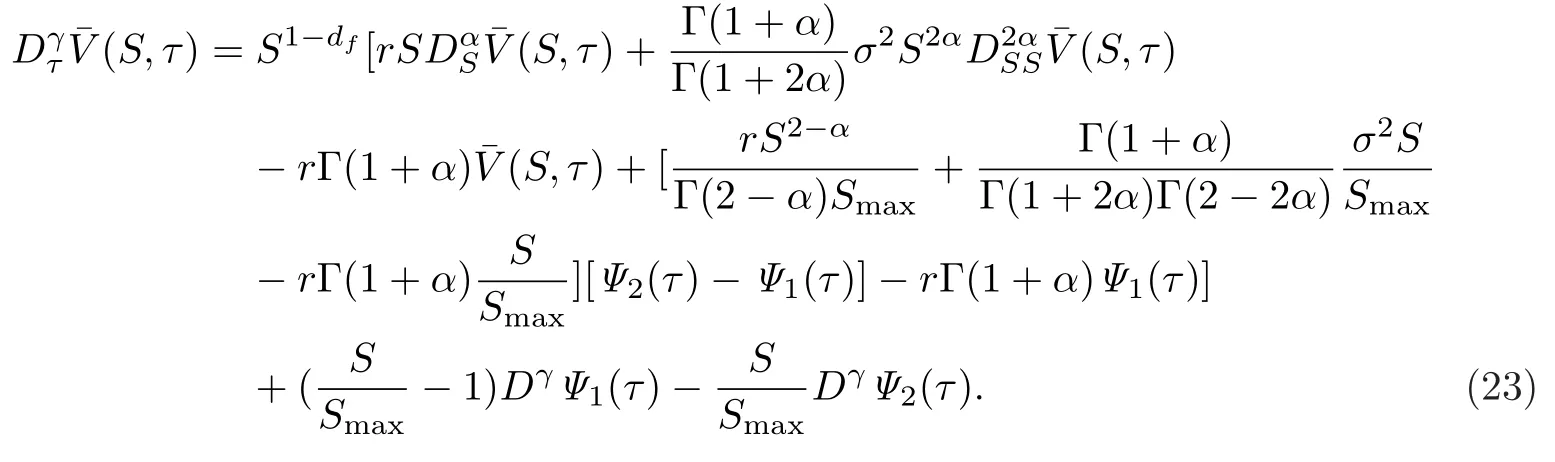
根据经典的Adomian分解法[33]，可以构造以下一阶近似解，

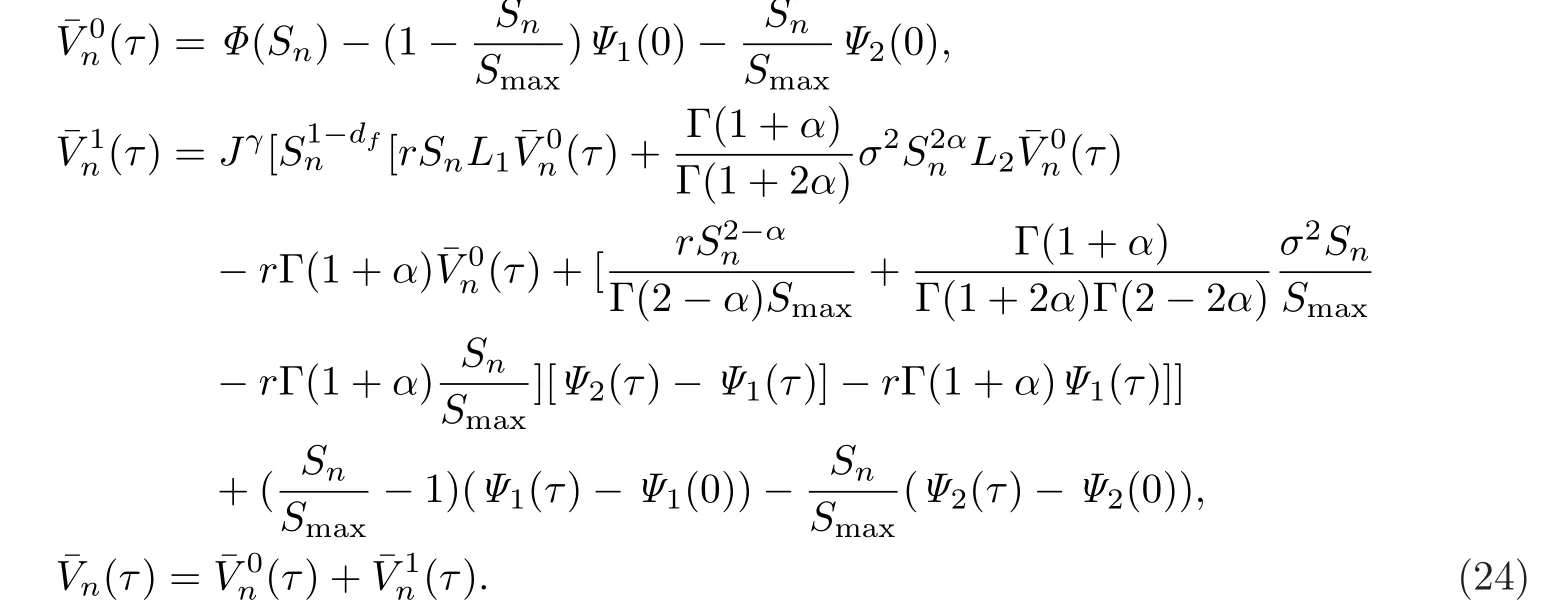
这里Jγ表示Riemann-Liouville分数阶积分算子，即

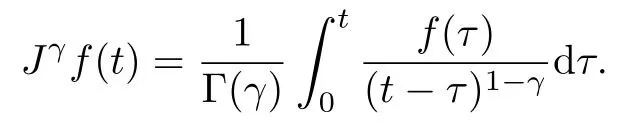
将该积分算子作用于Caputo分数阶导数得到等式

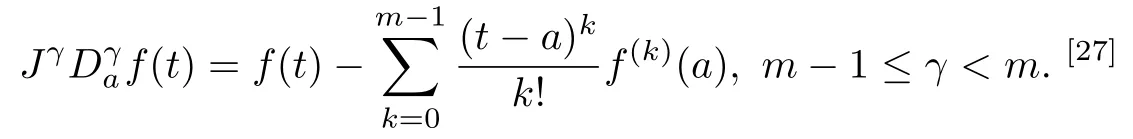
在空间变量离散的框架下，本工作采用优化技术获得半解析解，

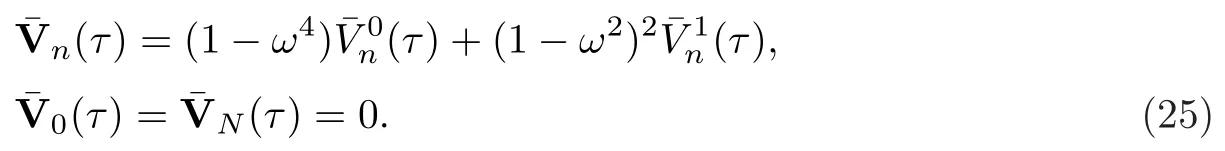
其中ω是收敛控制参数.

更一般地，可以建立以下表达式定义的级数解，

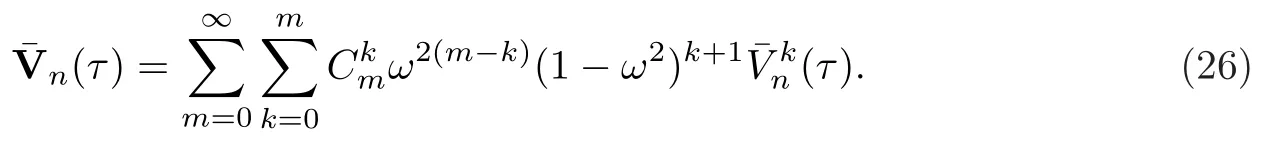
§4 应用与分析

借助于数学计算软件Matlab，将§3的结果应用到期权市场.在对沪深300ETF期权和上证50ETF期权进行应用分析的同时对所建立的时空分数阶导数期权定价模型进行解释.

例4.1应用半解析结果(25)和下面初边值条件估计欧式看涨期权.

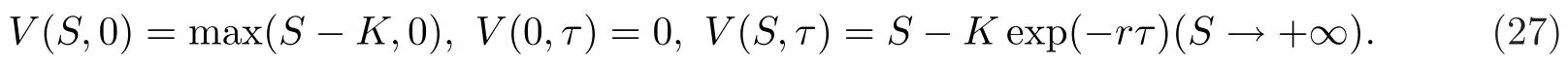
数据来源:上证50ETF，沪深300ETF和相应的期权数据来自中银证券交易软件

沪深300ETF在2019年的历史波动率σ是0.1980，R/S分析法给出Hurst指数是0.6773.分数阶导数定价方程(5)中的参数df是一个Hausdorff维数.文献[34]建议分形维数可以近似等于2-Hurst指数，所以df取为1.3227.也就是说，由沪深300ETF组成的分形介质的分形维数可以看作是1.3227.以执行价格K4.5的沪深300ETF期权10002221作为样本进行应用分析.无风险利率r取作电子储蓄债券的利息，约等于0.04.不失一般性，随机选取2020年2月17日的交易数据τT -tSt4.064，Vt0.0596，估计次日的期权价格，并将2020年2月18日的St取为开盘价4.057.图1展示分数阶导数的阶数，波动率，期权价格之间的关系曲线.令ω为0.1，在交易日2020/02/17，时间变量的分数阶导数γ与波动率σ之间的关系曲线如图1(a)所示.这里，选择α ＞0.5.同时，当时间和空间分数阶导数的阶数取不同值时，交易日2020/02/18的波动率σ与期权价格V(S，t)的关系曲线如图1(b)所示.

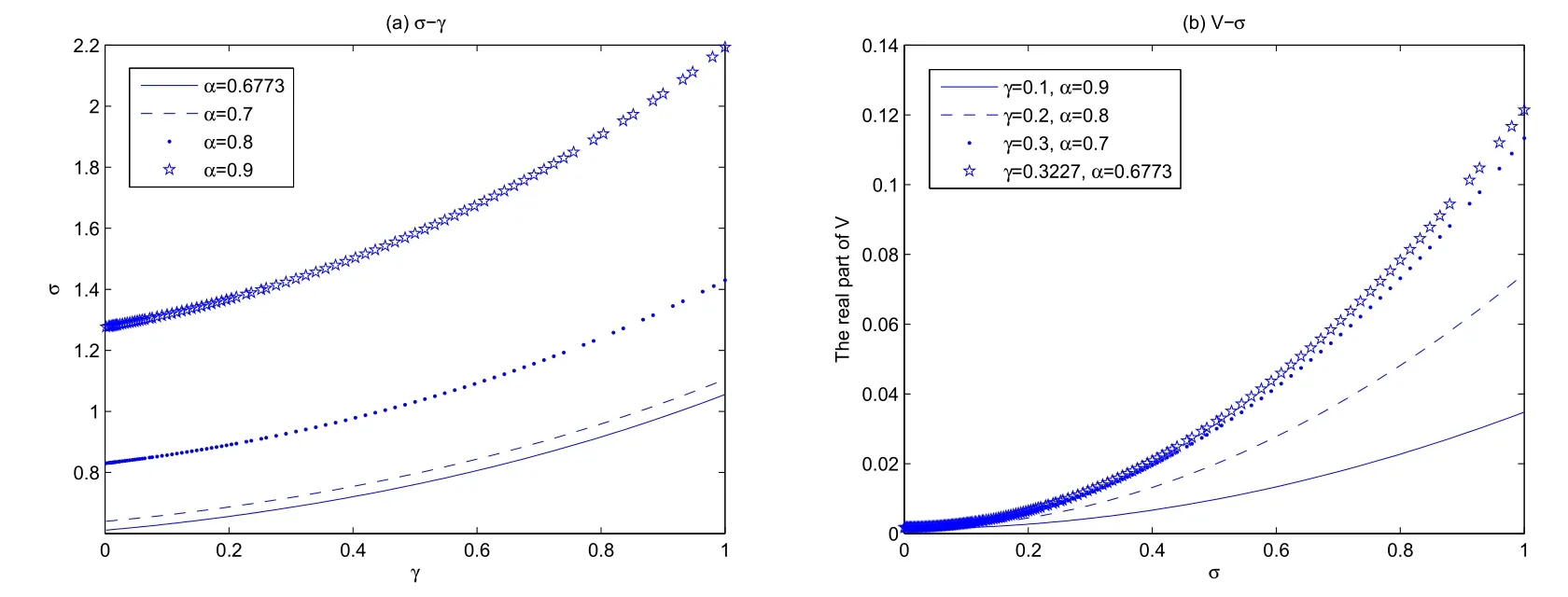
图1 关系曲线

当α0.6773和σ0.1980时，参数ω与γ在2020年2月17日的函数关系如图2所示，得到四组关系式.如果γ0.3772，按图2显示的关系式计算ω为±0.52803947∓1.1067955·10-16i和±2.0809089·10-16∓0.73458464i.交易日2020年2月18日的标的物沪深300ETF的价格St取为开盘价St4.057，利用本文的结果可以得到期权的价值为0.059198276-1.1156883·10-16i和0.060233499-2.6784167·10-16i.当日实际值为0.0606.在γ分别取作0.3772 和0.6773，其他参数不变的情况下，观测范围扩大为2020年01月02日-2020年06月22日的交易日.本工作的估计值，分数次Black-Scholes公式[10]，Black-Scholes公式和实际值一同绘制在图3中.实际上，结果有四组数值，由于数值彼此之间的差距并不明显，所以本工作选择其中一组值来绘制曲线.通过与真实值的对比，图3显示本工作的结果是有效的.

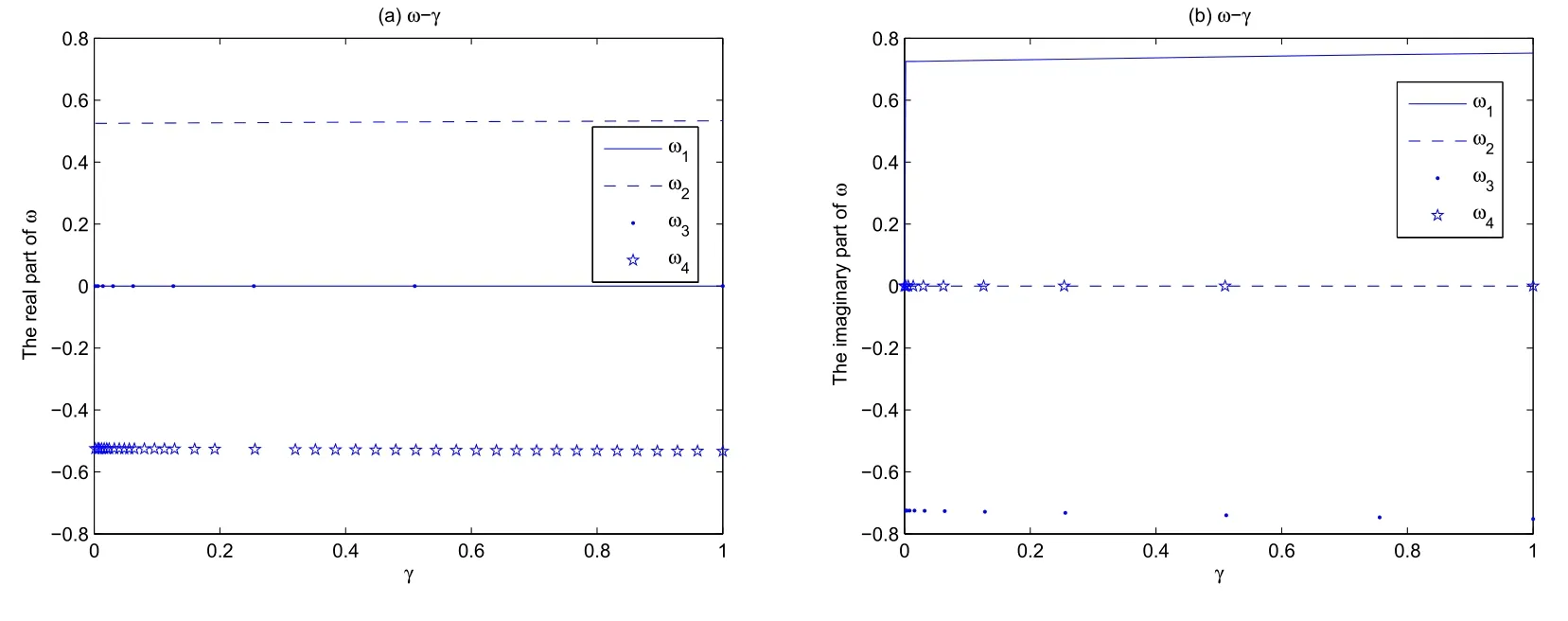
图2 曲线ω-γ

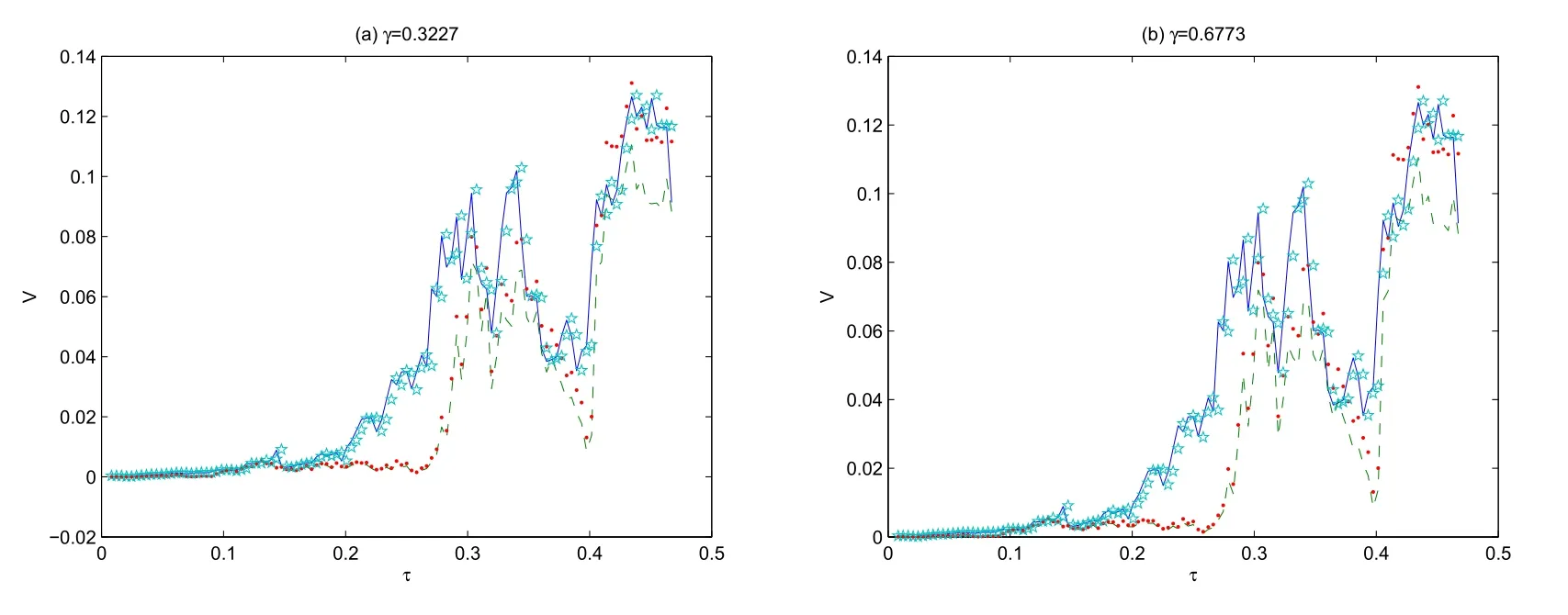
图3 α0.6773时欧式看涨期权价格对比

例4.2分数阶导数期权定价模型在欧式看跌期权中的应用.

该例所需满足的初边值条件为

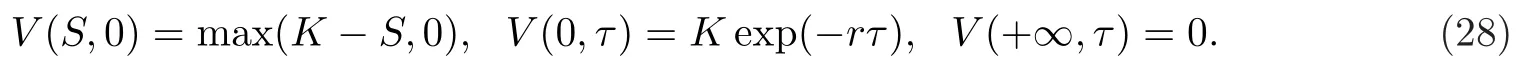
以沪深300ETF期权10002230于2020年1月8日-2020年6月22日的交易数据为样本，其执行价格K为4.6.根据例4.1，确定参数

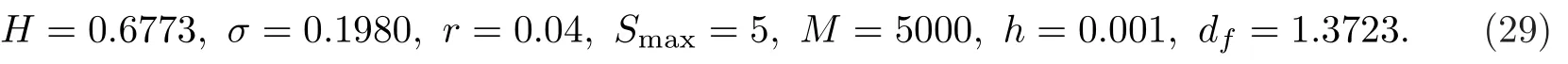
首个交易日，ω值选择0即可.之后，利用前一交易日的沪深300ETF实际收盘价和沪深300ETF期权价格决定ω值.当日期权价格的计算采用沪深300ETF的开盘价格.重复例4.1的计算过程，图4描绘2020年01月09日-2020年06月22日的沪深300ETF期权价格的比较.其中，分数阶导数α的值除取Hurst指数外，还任意取为0.9，来显示分数阶导数取不同值时期权价格的对比.同时，图5给出相应的误差对比图形，描绘的是本工作的结果，分数次Black-Scholes模型，标准Black-Scholes模型和真实值之间的绝对误差的对比.从图4和图5可以得出结论:本文的算法是有效的.并且发现:当时间和空间分数阶导数的阶数取不同值时，图4和图5中图形(a)和(b)的走势是相似的.

图4 欧式看跌期权价格对比

图5 误差对比

例4.3应用时空分数阶导数模型估计美式看跌期权.

定价美式期权与定价欧式期权的主要区别在于美式期权需要考虑提前行权的可能性.为避免套利，期权在每一点的价值不能小于内在价值.对于这一点的数学描述，采取一种简洁且有效的方法.在初边值条件(28)基础上，美式看跌期权的早期最优执行需要满足下面表达式

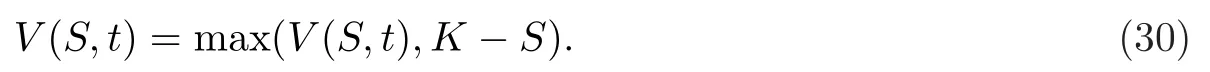
由于美式期权数据获取的局限性，本工作借用上证50ETF期权10002001的数据确定参数ω值，进而绘制在分数阶导数取不同值时美式看跌期权的价格曲线.应用例4.1中提到的估计方法，确定参数

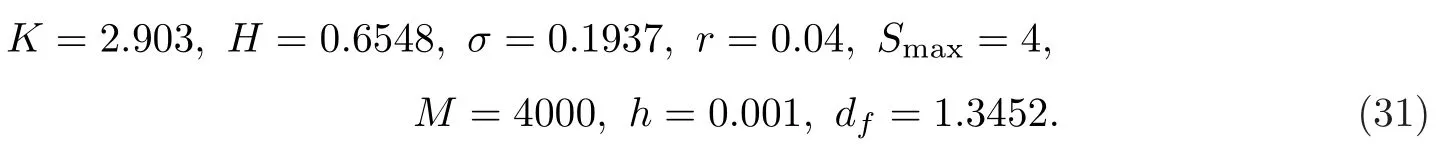
在每个时间点上，期权价格应满足以下等式，

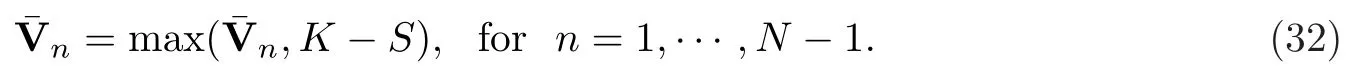
随机绘制一组结果.图6显示2019年10月24日-2020年6月22日的交易日中，美式看跌期权分别在γ0.3452，α0.6548和γ0.2，α0.7时的价格变化.在分数阶导数的阶数取不同值时，模拟美式看跌期权的变化趋势，结果符合规则，是可以理解的.

图6 美式看跌期权

§5 结论和讨论

本工作在Caputo分数阶导数定义下，研究基于时空分数阶偏微分方程的期权定价问题.以标准欧式和美式期权问题为例，利用内地金融市场沪深300ETF期权和上证50ETF期权的数据说明本工作的实际效用.以下是对整个工作的总结和进一步的讨论.

不同于已有文献[16-17，22-26]，本工作的模型是在Caputo分数阶导数定义下采用对冲技术建立的.众所周知，Caputo分数阶导数在物理力学等方面表现出优越性.由于分数阶微积分自身的复杂性，导致期权定价模型的建立存在诸多困难.本工作为建立新型模型，假设分数阶导数期权定价模型的解是一个变量可分离的函数，基于假设I-III，利用套期保值技术推导出单参数分数阶方程(13)，然后利用Heuristic Argument构造双参数方程(16).最后，通过将终端条件转换为初始条件得到Caputo型时空分数阶导数期权定价方程(5).

建立分数阶导数期权定价模型求解的改进框架.求解Caputo分数阶导数模型是一个棘手的问题，所以只取到一阶近似.对于这样结果，如果只在标准的Adomian 分解法下进行，很显然得到结果是不理想的.为此，从解法上给以修正，加入收敛控制参数ω.基于同伦分析方法[35]，文献[23]提出优化的Adomian分解法.本文用ω2代替文献[23]优化算法中的ω.显然，这种优化算法是灵活的，多样的.在对空间变量离散情况下，沿时间变量方向应用改进的Adomian分解法.从结果中可以看出，本工作建立的优化算法是可行且有效的.该改进思想可以应用于广义微分变换法，摄动法等诸多解析方法中，可以用于求解整数阶和分数阶偏微分方程.

在变量可分离的假设下，建立方程(5).并在半离散框架下，处理基于方程(5)的期权问题.诸多计算过程存在误差.在实际应用过程中，除利率r，波动率σ等常规参数外，本工作特别需要估计参数df，α，γ，ω.参数df，γ，α分别表示分形介质的维数，时间和空间分数阶导数的阶数，是体现分形特征的重要指标，能充分地反映市场的分形结构.但是，不可否认，更多参数的参与会导致更大的误差，并直接导致论证的复杂性.为此，本工作利用ω值来减少误差，利用前一天的收盘价数据确定ω值，来计算当天的期权价格.

在实证分析过程中，本工作采用开盘价计算当日期权价格.这种设计的优点是市场参与者可以利用沪深300ETF和上证50ETF的开盘价提前估计期权的收盘价，以便对实盘操作进行及时有效的调整.本文不仅尝试在Black-Scholes期权定价模型中引入Caputo分数阶导数，而且考虑实际的期权交易操作，有利于分数阶导数期权定价模型的理论和实践研究.