迭代函数系统的伪轨特殊性和平均跟踪性质

曾 鹏，李远飞

(广州华商学院 数据科学学院，广东广州 510000)

§1 引言

跟踪理论已经成为动力系统中非常重要的一个理论分支，特别是在结构稳定性理论中扮演着非常重要的角色[1-2].平均跟踪性质的概念最早是由Blank[3-4]给出，并且证明了某些摄动双曲系统具有平均跟踪性质.自平均跟踪性质概念问世以来，越来越多的学者开始关注各种类型的跟踪性质，对它们与动力系统所熟知的其它概念的关系进行了深入的研究，并取得了一些有价值的成果[5-11].

迭代函数系统是分形理论的重要分支，最早可以追溯到Hutchinson[12]构造了Rn中的有限个相似的压缩映射族来对分形集的自相似性研究，它是分形图像处理中最富生命力并且最具有广阔应用前景的领域之一，1985年，Barnsley[13]发展了这一分形构型系统，并命名为迭代函数系统(IFS).近年来发现动力系统中的很多重要的概念，如吸引子，极小性，传递性等都能够被推广到迭代函数系统[13-15].

自Glavan和Gutu在文[15]中定义迭代函数系统的伪轨跟踪性质以来，受到越来越多的学者对这方面的关注[15-21]，他们将多经典动力系统中的各种跟踪性质都引入到迭代函数系统中来，并且获得了一些比较好的性质.如Bahabadi[17]介绍了迭代函数系统的平均跟踪性质，并且证明了一个迭代函数系统具有平均跟踪性质当且仅当它的斜积变换具有平均跟踪性质;Nia[18]引进了迭代函数系统的渐近平均跟踪性质，并将经典动力系统中渐近平均跟踪性质的相关性质都推广到了迭代函数系统中;Shabani[20]给出了迭代函数系统中的遍历跟踪性质并研究了其与拓扑混合，链混合，跟踪性之间的一些关系.

紧致度量空间连续映射的特殊性最早是由Bowen在文[2]中为了研究公理A微分同胚的遍历性质引入的，Fakhari和Ghane在文[7]中定义了伪轨特殊性并研究了它与遍历跟踪性质的关系.最近，Shabani[20]将伪轨特殊性的概念推广到了迭代函数系统.

本文主要研究迭代函数系统中的伪轨特殊性和平均跟踪性质的相关关系，并且证明了下面的结论.

1.如果IFS(F)有伪轨特殊性质，则它有平均跟踪性质;

2.如果IFS(F)有平均跟踪性质并且F中某些f有稠密的-回复点，则IFS(F)是拓扑传递的.

§2 预备知识

记Z+为非负整数集，N为正整数集.在经典的动力系统中，称偶对(X，f)是一个拓扑动力系统，其中(X，ρ)是一个紧致的度量空间，f:X →X为连续的映射.

设(X，ρ)是一个紧致的度量空间，对任意，ε ＞0，记B(x，ε):ρ(x，y)＜ε}.设A ⊂Z+，用|A|表示集合A的个数，用d(A)表示集合A的密度，且

由字符{0，1，···，m-1}组成的所有的单边无限序列集定义为

设(X，ρ)是一个紧致的度量空间，fi:X →X(i0，1，···，m-1)为连续映射，则F{f0，f1，···，···fm-1}为作用在X上的连续映射族，则称迭代函数系统为由F作用在X上所生成的半群，记为IFS(F).Z+，及ωω0ω1ω2，称序列为IFS(F)的轨道，即

定义2.1[18]设IFS(F)为迭代函数系统.

(1) 对任意的非空开集，若存在Z+和使得∅，则称IFS(F)是拓扑传递的.

(2) 对任意的非空开集，若存在N ＞0，对任意的n ＞N，有Ø，则称IFS(F)是拓扑混合的.

(3) 对任意的以及任意的δ ＞0，若都存在一条从x到y的δ-链(伪轨)，则称IFS(F)是链传递的.

定义2.2[13-14]设IFS(F)为迭代函数系统.

(1) 设δ ＞0，若存在正整数NN(δ)及使得∀n ≥N(δ)和非负整数k，有

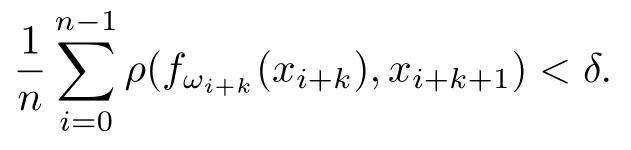
则称序列{xi}iZ+是IFS(F)的一条δ-平均伪轨.

(2) 若对于任意的ε ＞0，存在δ ＞0，使得对任意的一条δ-平均伪轨都能被X中的点ε-平均跟踪，即存在，使得

则称IFS(F)有平均跟踪性质.

定义2.3[21]设IFS(F)是一个迭代函数系统，[0，1).如果对任意的ε ＞0，存在δ ＞0使得IFS(F)中任意的一条δ-平均伪轨，都能被X中的点z，ε-q-跟踪，即存在，使得＜ε}＞q，则称IFS(F)有-平均跟踪性质.

定义2.4[20]设IFS(F)是一个迭代函数系统.IFS(F)有伪轨特殊性是指对于任意的ε ＞0，存在δδ()＞0和KK()＞0，使得对任意的非负整数

§3 伪轨特殊性与平均跟踪性质

本节主要证明如果IFS(F)有伪轨特殊性质，则它有平均跟踪性质.该结论可由文献[17，19，21]间接获得，受文献[8]的启发，下面给出一个直接证明的方法.

定理3.1设IFS(F)是一个迭代函数系统.如果IFS(F)有伪轨特殊性质，则它有平均跟踪性质.

设lsM+t，s ≥0，0≤t ＜M.则|{i ≤n，ρ(fωi(xi)，xi+1)≥δ}|＜s+1，否则

与(1)式矛盾.因此有

设X是紧致的黎曼流形.称迭代函数系统IFS({f0，···，fm-1})是 扩张的(参见文献[20])是指对任意的{0，1，···，m-1}，fi为C1-扩张映射.即，存在常数C ＞0和λi(0，1)满足对任意的N和，有‖

例3.2设映射f0，f1作用在S1上，定义

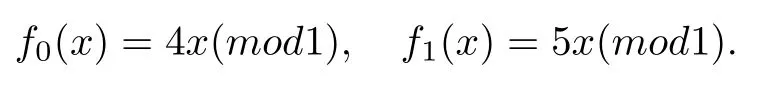
显然，IFS({f0，f1})是扩张的.则由文献[20]中引理6.4和注记6.2可知IFS({f0，f1})有伪轨特殊性质.从而根据定理3.1 知，IFS({f0，f1})有平均跟踪性质.

下面的例3.3来自文献[20]中例7.1.

例3.3设X{a，b，c}，ρ为离散的度量.其中a，b，c为X中三个不同的点.对任意的定义f0(x)a，f1(x)b，f2(x)c.则f0，f1，f2是X上的连续映射.设F{f0，f1，f2}.文献[20]中作者证明了IFS(F)有伪轨特殊性，从而根据定理3.1知，IFS(F)有平均跟踪性质.

§4 传递性与平均跟踪性质

文献[10]中证明了f有平均跟踪性质且具有稠密的-回复点，则f是拓扑传递的.本节证明如果IFS(F)有平均跟踪性质且满足F中某些f有稠密的-回复点，则IFS(F)是拓扑传递的.

首先需要下面的引理4.1和引理4.2(见文献[10]中引理4.1和引理4.2).

下面的引理4.3来自文献[21]中的定理6.2.

引理4.3设IFS(F)是一个迭代函数系统.则IFS(F)有平均跟踪性质当且仅当对任意的[0，1)，IFS(F)有-平均跟踪性质.

定理4.4设IFS(F)是一个迭代函数系统.如果IFS(F)有平均跟踪性质且满足F中某些f有稠密的-回复点，则IFS(F)是拓扑传递的.

根据引理4.1有

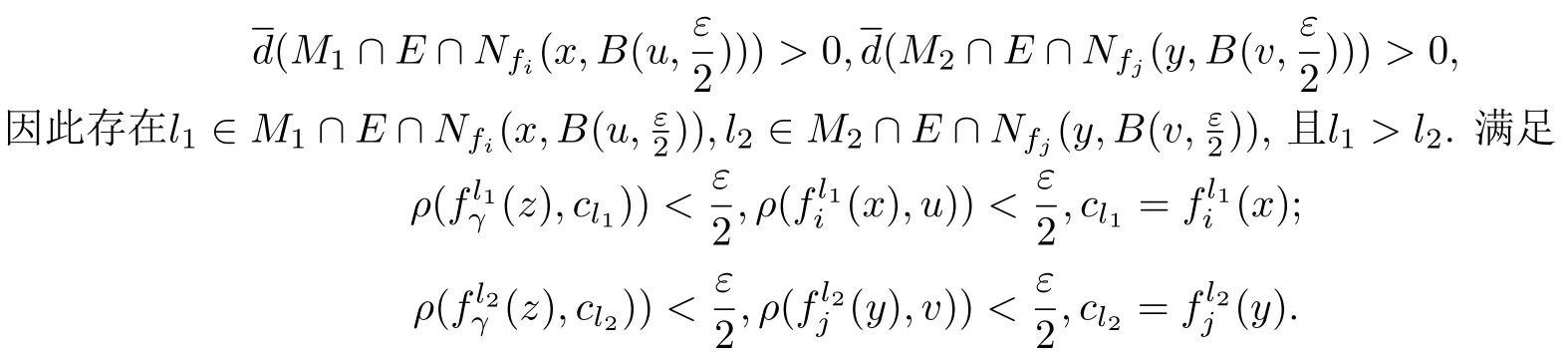
从而有

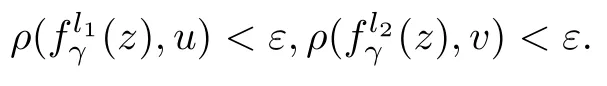
所以

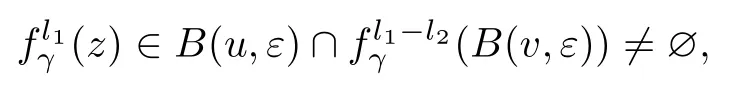
因此IFS(F)是拓扑传递的.

由定理3.1和定理4.4，可以得到下面的推论4.5.

推论4.5设IFS(F)是一个迭代函数系统.如果IFS(F)有伪轨特殊性且满足F中某些f有稠密的-回复点，则IFS(F)是拓扑传递的.

下面给出一个具有平均跟踪性质但没有拓扑传递性的例子(可参见文献[21]例6.5)

例4.6设映射f0，f1作用在[0，1]上，定义

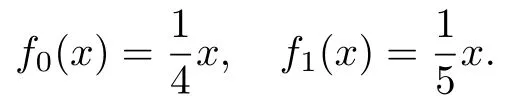
则由文献[16]中定理2.1知，IFS({f0，f1})有平均跟踪性质.但是IFS({f0，f1})不是拓扑传递的.

致谢感谢审稿人的仔细阅读以及相关建议，本文受广州华商学院科研项目资助.