基于AR模型的海上风机脉动风速时程模拟

骆光杰，朱洪泽，郭 健，苏 凯，3，4

(1.浙江华东工程咨询有限公司，浙江 杭州 310014；2.水资源与水电工程科学国家重点实验室(武汉大学)，湖北 武汉 430072；3.武汉大学水工岩石力学教育部重点实验室，湖北 武汉 430072；4.武汉大学海绵城市建设水系统湖北省重点实验室，湖北 武汉 430072)

0 引 言

近年来风电新能源行业不断发展，近海风机由于其具备占地少、噪音小，风资源丰富等优势[1]成为当前风电能源发展的首选。对于兆瓦级风机而言，由于结构高耸且柔性较大，同时，海上运行条件复杂多变，尤其以风荷载变化最为明显，对结构安全提出了严峻考验。无论采用叶素-动量定理[2]或简化伯努利方程[3]计算风机荷载，还是通过指数律风轮廓线计算塔筒风荷载[4-5]，均需要首先获取结构风速变化情况。重大工程建设中，常采用风洞试验或现场实测等手段确定风荷载，但前者耗资巨大，并且结果不具普适性[6]，后者存在布设困难，并难以获取整体风场分布情况。基于数值模拟方法，可利用较少数据快速获取大量代表性风速时程曲线，在风机结构设计和强度校核过程中，具备突出的作用和意义。相关数值模拟方法主要有线性滤波法、谐波叠加法、逆傅里叶变换法、小波分析法等[7]，不同方法存在各自优缺点，但线性滤波法中自回归模型(Auto-regressive model， AR)拥有计算量小和速度快的特点，近年来在相关领域研究中使用较多。温鹏等[8]通过自回归算法对陆上风机进行风速模拟，同时利用模型残差平方和进行模型阶数判定；刘文洋等[9]针对大跨度空间结构，设计MATLAB程序以实现风速记录模拟与整理存储；张文福等[10]针对细化的标量过程AR模型和向量过程AR模型，从计算精度及效率角度出发进行了讨论分析；舒新玲等[11]通过VC和MATLAB混合编程实现空间风速场的模拟。

本文根据海上风机的体形特征，采用线性滤波法中的自回归(AR)模型，利用MATLAB平台编制了海上风机脉动风速时程模拟程序，并基于江苏黄海某风机工程项目，进行实际案例计算。同时，采用美国可再生能源实验室(National Renewable Resource Laboratory， NREL)开发研制的TurbSim[12]软件进行结果对比。

1 脉动风基本特征

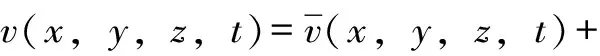
(1)

式中，x、y、z分别代表空间中任一点的三维坐标；t为某一时刻。其中平均风认为是周期在10 min以上的风速幅值不变部分，并且平均风风速沿高程方向的幅值变化规律可用指数函数表示，即

(2)

而脉动风是由风的不规则运动产生，在工程中常假定为平稳随机过程，即在任意时刻的风速概率分布完全相同的随机过程。因此常通过功率谱函数进行时域上的脉动风速时程模拟。目前，根据对强风观测记录处理方式的不同。存在两类常用于海上风机结构设计的脉动风速功率谱(power spectral density， PSD)，包括Davenport谱[15]、Kaimal谱[16]、Von-Karman谱等[17-20]。常见功率谱如表1所示，其中Kaimal风速谱由于计算简单，并且考虑了风速谱随时间变化情况，美国、欧洲规范均采用该风速谱用于风荷载模拟等问题研究[4]，本文即采用该风速谱进行计算，风速谱模型示意如图1所示。

表1 常用脉动风速功率谱

图1 Kaimal风速谱

2 基于AR模型的脉动风速时程模拟

AR模型是将均值为0的白噪声随机序列通过滤波器，使其输出具有指定谱特征的随机过程[21]。由于不涉及其他变量，整体计算相对简单，非常有利于脉动风速时程的模拟。

2.1 AR模型基本方程

采用AR模型对空间风场进行模拟时，需要考虑风的空间相关性，因此将式(1)扩展至空间M点形成基本方程，可表示为

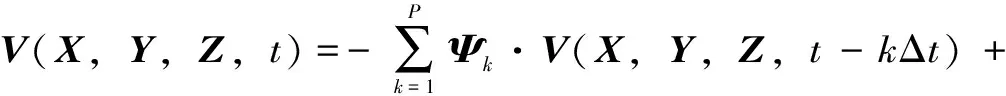
(3)

其中，

X=[x1，x2，…，xM]T

(4)

Y=[y1，y2，…，yM]T

(5)

Z=[z1，z2，…，zM]T

(6)

N(t)=L·n(t)

(7)

式中，(xi，yi，zi)为空间第i点坐标，i=1，2，…，M；V(X，Y，Z，t)、V(X，Y，Z，t-kΔt)分别为空间各点在t时刻及(t-kΔt)时刻的脉动风速时程向量；p为AR模型阶数，可根据AIC准则(最小信息准则)选取，通常取p=4；Δt为模拟风速时程的时间步长；Ψk为AR模型自回归系数矩阵，为M×M阶方阵；L为M×M阶下三角矩阵；n(t)是M维均值为0、方差为1相互独立的白噪声向量。为简化表述，将V(X，Y，Z，t)简写为V(t)。

根据自相关函数的性质，对式(4)两侧同乘VT(t-jΔt)，并做数学期望计算，得到

(8)

进一步简化为矩阵形式(正则方程)，即

(9)

d=L·LT

(10)

Ψ=[I，Ψ1，…，ΨP]T

(11)

式中，Ψ为(p+1)M×M阶矩阵；I为M阶单位阵；O为PM×M阶零矩阵；R为(p+1)M×(p+1)M阶相关函数Toeplitz矩阵，其表达式为

R=

(12)

需要特别注意的是，R矩阵中任意元素R(kΔt)均是M阶方阵，k=0，…，p，表示为

式中，矩阵中各元素Rij(kΔt)代表时间相差kΔt时，空间任意两点i与j间的相关函数，其中i，j=1，…，M。

2.2 求解自回归系数矩阵

对于自相关矩阵R，可由Wiener-Khintchine公式可知式(13)矩阵中各元素Rij(kΔt)可由功率谱函数表示为

(14)

式中，当i=j时，功率谱函数Sij(f)即为自功率谱密度函数；而i≠j时，则称为互功率谱密度函数，并且可由两点处自功率谱函数求得，计算公式为

(15)

式中，Cohij(f)为空间两点间相干函数[22]，用以表示风速时程的空间相关特性，其三维表达式为

Cohij(f)=

(16)

通过选择表1中脉动风速谱模型，可计算空间M点各点自功率谱密度函数，再由式(14)～(16)可得到相关系数矩阵R，求解正则方程可得到AR模型自回归系数Ψ和矩阵d。

2.3 求解随机过程

对求解得到的d矩阵进行Cholesky分解，可得下三角矩阵L，进而通过随机白噪声向量n(t)得到独立随机过程向量N(t)。通常为方便计算，假定初始时刻及之前时刻各点风速均为0，即：t≤0时，V(t)=0。在此基础上，将自回归系数Ψ和矩阵d代入基本方程(1)并可表示为

(17)

3 工程实例模拟

依据前文所述基本求解思路，本文利用MATLAB数学分析平台，编制基于AR模型的模拟程序，以对风机塔筒、叶轮等空间多点脉动风速时程进行模拟。

江苏黄海如东海域某4 MW近海风机塔筒高度为81.25 m，叶轮直径为146 m。计算模型简化为平面结构，采用笛卡尔直角坐标系，原点位于风机塔筒与海平面交界处，水平方向为X轴，Y轴以竖直向上为正。塔筒部位共模拟8点，叶片各模拟3点，各模拟点基本位置如图2所示。本文目标谱采用Kaimal风速谱，模拟主要需要场地参数、频域模拟参数以及AR模型参数等。根据项目资料确定场地类型为A类，10 m处多年平均最大风速为8 m/s；频域起始模拟频率定为0.001 Hz，截断频率为10 Hz，共划分为1 000份；采用4阶AR模型，模拟总时长为100 s，时间步长为0.01 s。

图2 海上风机简化计算模型(单位：m)

同时，本文采用TurbSim程序进行对比分析，该软件常用于生成海上风机结构的风速入流条件，支持自定义气象边界和模型条件，并可输出不同文件类型全域风速时程数据，以辅助各类结构分析软件计算，例如OpenFAST、Bladed等。

限于篇幅限制，本文仅选取节点8、11号进行比较。如图3、4所示，分别为各点风速时程及功率谱密度函数模拟结果对比。

图3 风机部分控制点风速时程

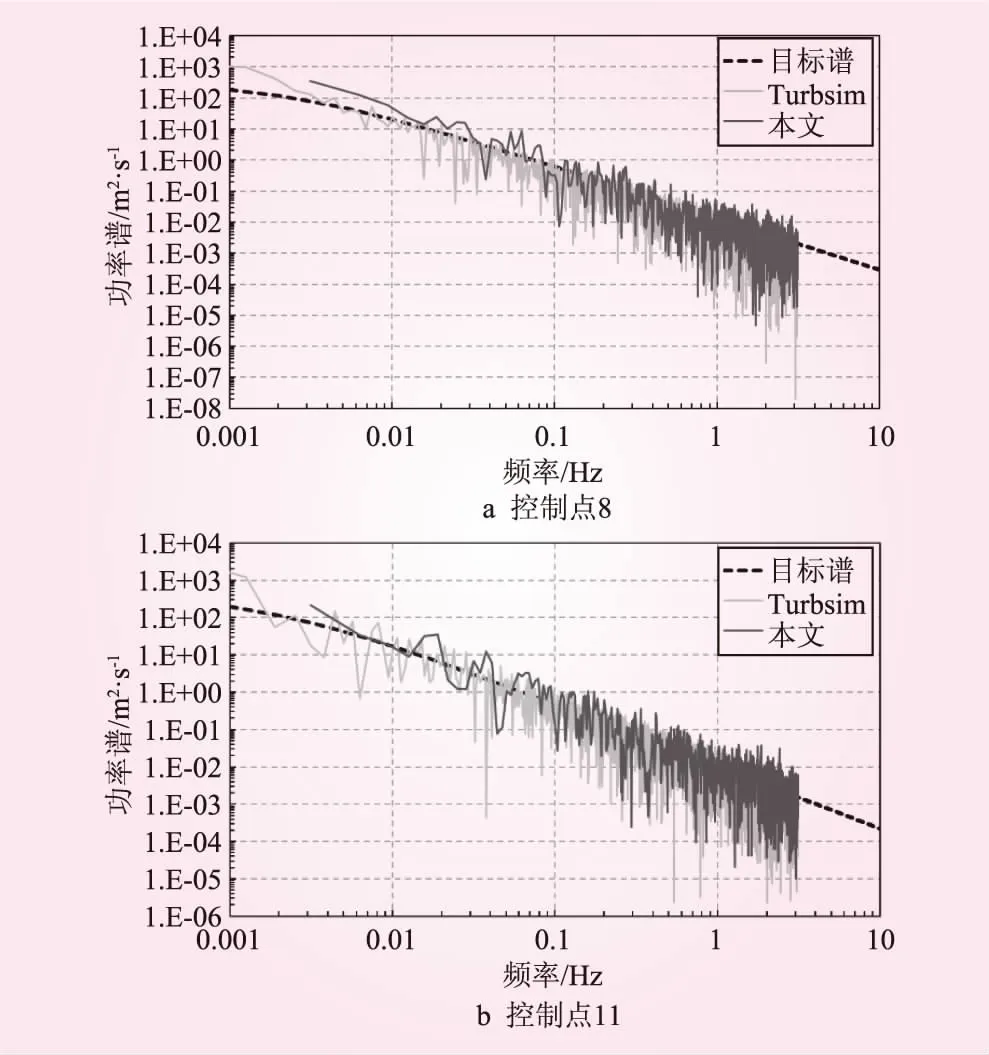
图4 风机部分控制点功率谱

由图3可以看出，本文采用AR法得到的控制点整体风速波动大于TurbSim程序模拟结果，这是因为AR模型中无法定义湍流强度，而在TurbSim程序中可通过IECturbc (IEC turbulence characteristic)进行定义。在频域中，两者风速功率谱模拟结果基本一致，并且与Kaimal目标谱拟合效果良好，达到预期目标。

同时，需要注意的是，TurbSim程序模拟风场时，需要预先设定空间网格，如图5所示。对于无法通过该网格确定的空间点，例如本文中叶片上控制点12～17，则无法直接获取，只能选择进一步提高空间点分布密度以获取相关结果，这无疑提高了计算成本。而本文对空间控制点没有预设要求，例如控制点12脉动风速时程如图6所示。

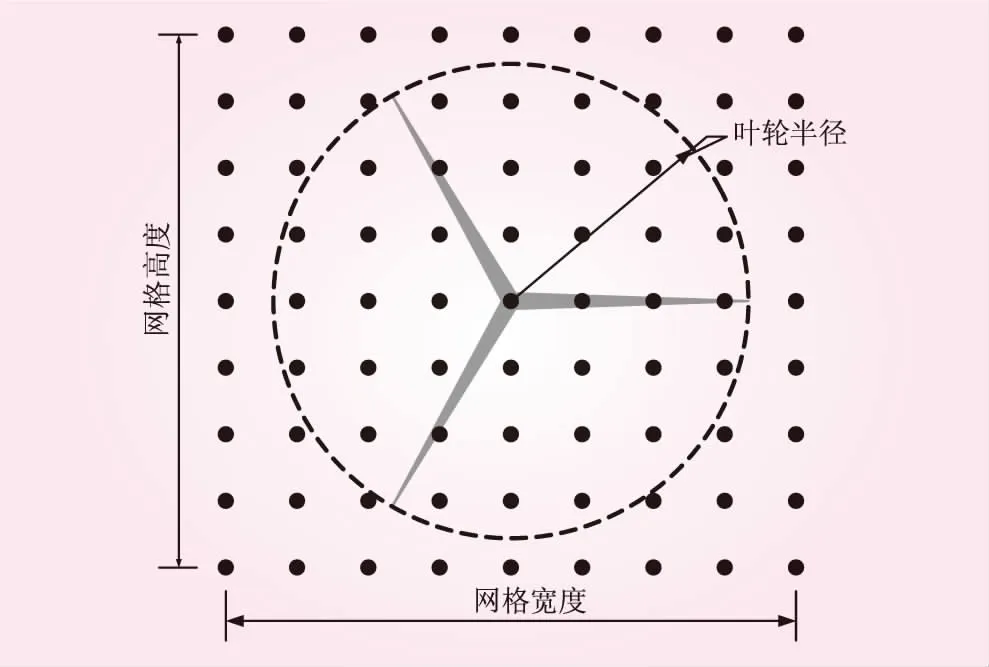
图5 TurbSim程序预定义网格

图6 控制点12号脉动风速时程

4 结 论

本文基于线性滤波法中自回归模型及Kaimal脉动风速功率谱，编制了相关空间域脉动风速时程模拟软件，并根据江苏黄海某工程实际确定基本参数，对海上风机结构脉动风场进行模拟计算，最后与TurbSim程序相对比。计算结果表明：

(1)对海上风机的脉动风速时程模拟时，采用AR模型仅需通过少量地域气象资料便可快速生成多组空间控制点脉动风速时程，同时计算过程迅速，操作简单。

(2)本文模拟结果虽然无法考虑湍流强度，但其功率谱密度函数与TurbSim程序结果及目标Kaimal功率谱谱拟合效果较好，整体模拟精确。同时，由于本文程序对计算控制点无任何要求，因此可广泛适用于各类风机结构。

(3)以当前自回归模型模拟海域脉动风速时，本文对风机风场进行了简化，未考虑塔影效应等影响，用于工程实际中时，仍需要辅以相关测风塔实测信息或气象记录。