基于小样本学习和生成式对抗网络模型的短期风电功率预测

栾 毅， 剡文林，刘 岩，杨永强

(1.云南电力调度控制中心，云南 昆明 650041；2.华北电力大学能源动力与机械工程学院，北京 102206)

0 引 言

风电是一种重要的低碳能源，它具有低成本、清洁、可再生等诸多优点，具有可持续能源供应的潜力[1]。风能固有的间歇性、随机性和波动性等特点给大规模风电并网的安全调度和平稳运营带来挑战[2]。准确的风电预测不仅可以有效解决风电消纳问题，也会增强风电在电力市场中的竞争力[3]。

风电预测问题属于数据密集型应用，其核心挑战是如何处理大量、复杂、丰富多样、快速变化的数据。机器学习在数据密集型应用中非常成功，但当数据集很小时，机器学习模型无法很好的学习到数据的完整特征[4]。国内外已有大量研究[5-7]表明，统计方法的模型并不直接建立风速与功率的物理关系，而是试图找出数据之间的映射关系，需要对大量的历史数据进行识别、拟合、训练，才能达到一定的精度。为了解决这一问题，近年来提出了小样本学习(Few-shot learning， FSL)[8]。利用先验知识，FSL可以快速地泛化到只包含少量有监督信息的样本的新任务中[9]。

本文主要开展了以下3方面工作：①针对区域电网内的风电场缺少大量历史数据的问题，本文提出了一种基于FSL的生成对抗网络(Generative Adversarial Network， GAN)[10]模型用以扩充样本集，从而更好地完成风电预测模型的训练与预测功能；②针对传统生成对抗网络模型无法处理回归问题的情况，提出了改进-生成对抗网络(GR-GAN)的模型，使其可以在样本有限的条件实现风电预测这一回归问题；③使用两个不同地区风电场的历史发电量数据集进行了实验验证，结果表明与基线方法相比，本文模型方法达到了最佳预测效果并且在输入较少样本时模型就表现出较小的预测误差。

1 算法理论介绍

1.1 小样本学习

机器学习(Machine Learning)是一种计算机程序，可针对特定任务T学习经验E，并根据性能评价指标P不断提高经验E在任务T上的表现。小样本学习(FSL)是一类机器学习问题(使用E、T、P表示)，其中对目标任务T，E只有有限数量的有标签信息。

目前的小样本研究主要聚焦在监督学习，具体可分为以下3类：小样本分类问题(Few-shot classification)，其目的是在对每一个类别都只有少量有标签样本的情况下学习一个分类器；小样本回归(Few-shot regression)，其任务则是在有限的输入-输出样本对上评估一个回归函数h，其中yi是因变量y的观测值，xi是模型输入，即自变量x的观测值；小样本强化学习(Few-shot reinforcement learning)，其目标是在少量状态-动作对的情况下学习强化策略。风电预测问题的预测目标变量是连续变量，因此属于一类回归问题，本文主要基于小样本回归实现风电预测。

1.2 生成对抗网络

GAN包括2个独立的深度网络：生成器和判别器。生成器接收一个随机变量z并将其映射到数据分布pdata(x)，其中z的分布为pz(z)。生成器的输出分布应收敛到训练期间的数据分布。判别器通过输出0或1来判别生成器产生的样本是否为真样本。在GAN的训练过程中，生成器和判别器分别用于生成样本和分类样本，采用对抗的方式提升彼此的性能。GAN采用对抗损失函数来训练生成器和判别器

minGmaxDV(D，G)=Ex～Pdata(x)[logD(x)]+
Ez～Pz(z)[log(1-D(G(z)))]

(1)

G(z)是生成数据分布，因此公式可以改为

minGmaxDV(D，G)=Ex～Pdata(x)[logD(x)]+
Ex～PG(x)[log(1-D(x))]

(2)

式中，maxDV(D，G)为最大化判别器D的价值函数。判别器的任务是，对于真数据，输出1；对于假数据，输出0。由此可知Ex～Pdata(x)[logD(x)]表示了真数据的价值，Ex～PG(x)[log(1-D(x))]表示假数据的价值，两部分的结果相加得到了判别器的价值函数，其数值越大表示判别器越准确。minG部分则是要最小化生成器G的价值函数，训练生成器时目标与判别器训练目标相反，希望D(x)接近与0，即迭代器对假数据的判断结果越错误越好，这样就表示了生成数据分布接近真实数据分布。

GAN算法的目的是推导出由两方参与的极小化极大算法的纳什均衡点(Nash-equilibrium point)[11]。在本文的风电预测算法中，针对风电场发电数据样本偏少的问题，基于GAN模型完成风电样本的生成与判定任务。

2 基于GR-GAN的风电预测模型

各地区风电场保存的历史数据包含了大量的缺失值，并且存在一些噪音，不利于算法模型的训练。因此首先需要对风电场原始数据进行数据预处理，得到标准的、干净的、连续的数据。

随后基于风电场的历史功率、历史风速、地形地貌、数值天气预报、风电机组运行状态等数据建立风电场的特征表达和融合，进而构建风电场输出功率的预测模型。受到改进的GAN技术的启发[12]，改进GAM模型，使其能够处理风电预测这一回归问题。本文应用GAN生成逼真的高质量样本，并预测与这些生成的样本相对应的连续标签。

最终对整个网络模型(包括生成器和判定器)进行训练，最终得到训练好的预测模型。以风速、功率或数值天气预报数据作为模型的输入，结合风电场机组的设备状态及运行工况，得到风电场未来的输出功率。具体流程如图1所示。

图1 GR-GAN模型流程

2.1 数据表示

针对风电场历史数据集中重要性相对较低的温度数据和湿度数据的缺失部分，基于温度数据与湿度数据服从正态分布的性质，使用期望值最大化方法(Expectation maximization，EM)进行填充。对于风力特征及其他重要性靠前且缺失率适中的特征参数，根据欧式距离确定缺失数据样本最近的K个样本，将这K个值加权平均来估计该样本的缺失数据，同时使用K最近邻模型(K-means clustering)预测补充缺失值。

2.2 预测模型构建

借鉴改进的GAN模型原理，提出了GR-GAN模型，重点是基于生成对抗网络的半监督学习来解决回归问题，它包含一个生成器和一个判别器，其中生成器负责生成接近训练集的真实样本；判别器用于验证生成的样本并且将这些样本预测成连续的标签。使用特征匹配技术训练生成器。判别器产生两个输出：一个用于预测风电场的功率标签，一个用于预测生成样本是真/假的概率。预测标签归一化到[0，1]范围后，在判别器网络的最后一层使用sigmoid函数进行非线性变换。

我们使用一个无监督GAN损失函数以及一个有监督回归损失训练判别器

(3)

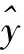
基于回归的GR-GAN模型结构如图2所示，其中D(x)和预测标签均使用卷积神经网络(Convolutional neural network， CNN)。其中，xgen为生成器产生的无标签风电场数据；xlabel为有标签的真实风电场数据；xunlab为无标签的真实风场数据。

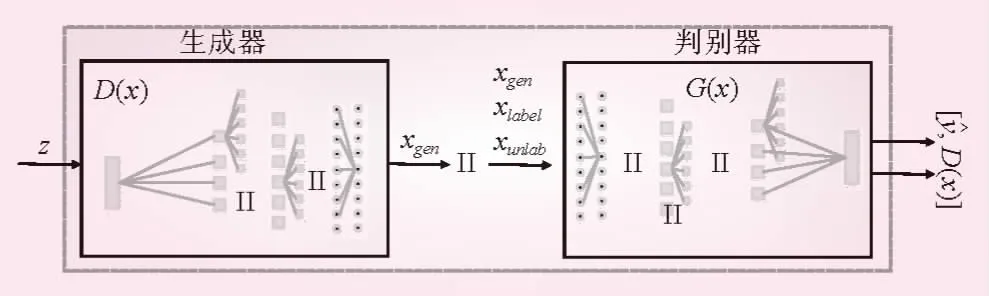
图2 GR-GAN模型结构示意

3 实验结果及分析

3.1 评价指标

为评估风电预测模型GR-GAN的准确性，选用2个指标作为评估标准。一是平均绝对百分比误差(Mean Absolute Percentage Error，MAPE)用于评估实时误差，代表线性回归损失，公式为

(4)

式中，n为数据集中包含风电场数据样本的天数；Wi为第i天的实际发电量，kW·h；W′i为第i天的预测发电量， kW·h。

另一个指标是均方根百分比误差(Root Mean Squard Percentage Error，RMSPE)用于评估预测期间的总体误差，代表误差的平方的期望值，表达式为

(5)

3.2 对比算法

为验证GR-GAN算法的生成对抗网络结构的性能及其对电场日风力发电功率的预测性能，使用原始生成对抗网络(Original-RGAN)、支持向量回归(Support vector regression， SVR)、长短期记忆(Long-short term memory， LSTM)算法进行对比验证。

Original-RGAN是以原始GAN模型为基础，在一个生成模型G、一个判别模型D上加入一个回归模型R。基于判别模型D通过对抗学习得到的一系列潜在特征层，通过R与D共享特征层可以提高风电预测回归模型R的性能表现。同时利用回归模型R估计生成模型G的条件变量与生成样本之间互信息的下界值，约束生成模型G使其产生更真实的样本。

SVR方法作为支持向量机(support vector machine， SVM)在回归问题上的应用，SVR方法使用核函数将风电场数据映射到特征空间并寻找一个最佳区域，再对区域外的点进行回归操作。

LSTM方法是LSTM网络，通过训练时在风电场时间序列上的反向传播来克服梯度消失问题，由于其易于处理时间序列的特性，可以用来构建大规模的递归神经网络来处理机器学习中复杂的序列问题，并取得不错的结果[12]。

3.3 仿真实验与结果分析

实验风电场的数据集分别来自新疆某风电场和内蒙古某风电场，前者保存了2015年～2018年的数据，后者保存了2014年～2019年的数据。将最后一年的数据作为测试集，其余作为训练集。模型对2个测试集的1月时间尺度预测结果如图3所示。

图3 实验对比

由图3可以看出，GR-GAN模型曲线与真实发电量曲线表现出相同的趋势，在所有模型中最接近真实发电量数据。通过观察可知，GR-GAN模型与其他三种模型相比大幅减小了误差，表现出最好的预测性能，证明了模型在风电预测问题的有效性；LSTM模型表现出比Original-RGAN模型更好的预测效果，这是由于LSTM模型基于风电场数据的时间序列建模，更好的表征了数据，而Original-RGAN模型虽然可以生成更多样本，但其内部结构简单的卷积网络层与回归模型制约了其预测效果；SVR方法表现出了最差的预测性能，这说明SVR这种基于机器学习的方法在本案例中不能很好表示风电场的数据特征。

本文同时验证了模型在少量样本情况下的预测性能，实验结果如图4所示，横坐标表示模型使用x天的训练数据，纵坐标为模型的平均绝对百分比误差。由图4可见，在训练的初始阶段，基于GAN模型的GR-GAN和Original-RGAN就表现出了较小的误差，而LSTM模型和SVR模型在实验初期误差较高，说明基于生成对抗网络的模型更适用于小样本的风电预测问题；随着加入训练的真实样本数越来越多，LSTM模型的误差小于Original-RGAN模型，说明在样本足够的情况下LSTM模型可以保持较好的预测性能。

图4 小样本实验对比

表1、2列出了两个数据集中小样本实验的误差，进一步证明了本文方法的有效性。实验分别使用了200、500、1 000 d以及全部真实样本进行训练，对比分析各模型的平均误差。由观察可知，GR-GAN模型相比Original-RGAN其MAPE降低了2.19%，这表明，GR-GAN中的无监督网络模型对生成样本有很好的增强效果；GR-GAN模型相比LSTM模型MAPE降低了0.33%，说明GR-GAN模型表现了较有竞争力的预测性能，与LSTM模型的全样本预测结果差别较小的原因可能是由于GR-GAN模型内部的CNN结构不能像LSTM模型可以对时间序列有更好的表示。

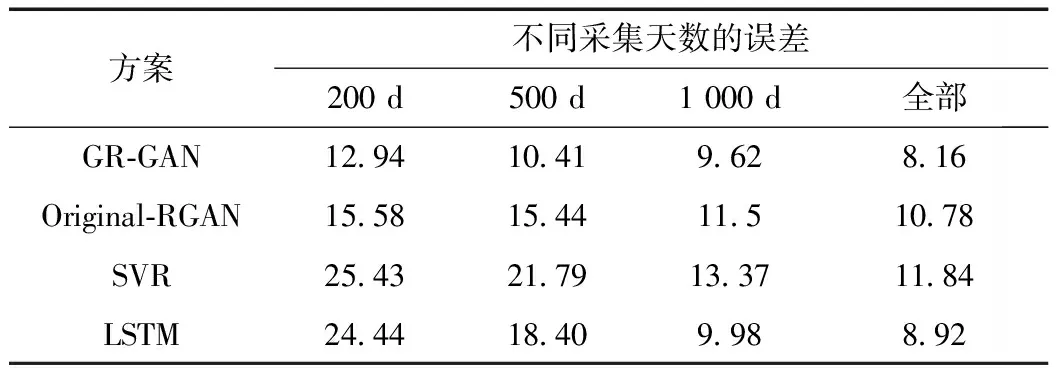
表1 小样本实验预测误差统计(新疆电场数据集) %

表2 小样本实验预测误差统计(内蒙古电场数据集) %

4 结 论

本文对新疆、内蒙古地区两个风力发电量的短期预测问题进行了研究，提出了一种基于小样本学习与生成对抗网络的风电发电量预测模型，在两个风电场数据集上进行了验证，结论如下：

(1)在多个对比方法中，基于GAN的方法在所有验证方法中表现最好，说明此类网络结构更适用于小样本的风电预测问题，其中GR-GAN模型体现出了最好的预测性能。

(2)在处理复杂风电数据时，基于深度学习的方法表现出更强的学习能力。

(3)LSTM模型对全样本训练的风电预测问题仍然表现了较小的误差，说明LSTM模型更适合处理风电数据所构成的时间序列，鉴于其既适用于风电预测的小样本学习，又能对时间序列进行更准确的预测，因此后续工作将进一步探索融合LSTM网络的GAN回归模型。