不同应力路径下砂岩分段变速连续卸荷变形特性研究
覃万里,艾洲洋,郑 莉,蔡 军
(浙江华东工程咨询有限公司,浙江 杭州 310000)
0 引 言
工程高陡边坡的变形不仅影响边坡施工期的稳定性,也对工程运营造成一定的安全隐患,高陡边坡岩体开挖卸荷中卸荷应力路径、卸荷速率对边坡开挖变形产生的影响较为显著。韩铁林等[1]在不同应力路径下对砂岩试样进行了三轴试验,对比分析了砂岩的强度、变形、破坏力学特性,得出了不同应力路径下砂岩侧向变形、强度特性和破坏特征的影响因素和变化规律。刘泉声等[2]通过对比不等量卸围压和轴压的原煤试验和不同围压下的常规三轴试验,研究了卸荷条件下原煤的变形、强度参数及破坏特征。王瑞红等[3]将砂岩三轴加载破坏试验与卸荷破坏试验进行对比,得出了岩体的峰值应变、残余应变与围压的关系,力学参数与卸荷量的关系以及变形参数与卸荷速率的关系。胡卸文等[4]通过对比红砂岩三轴加载和卸载试验,得出了2种不同应力路径下的变形破坏特征和强度参数差异。王兴霞等[5]在升轴压卸围压的应力路径下进行了砂岩的卸荷试验,重点比较了变形模量在三轴加卸载下的弱化规律,以及卸荷速率对变形模量的影响关系。戴兵等[6]基于不同应力路径下的卸荷试验,研究了3种不同方案下岩样轴向吸收应变能转化为扩容消耗应变能的程度,以及初始围压对3种应变能的影响程度和岩样存储弹性应变能的大小。郭喜峰等[7]在不同卸荷速率下进行了岩石的卸荷试验,根据应力-应变曲线特征,得到了破坏强度特征、变形参数随卸荷速率的变化规律。胡帅等[8]通过与循环加卸载试验的对比分析,研究在一种应力路径下,不同卸荷速率对花岗岩变形特征和强度破坏特点的影响。邓华峰等[9-10]研究了卸荷速率和孔隙水压力对岩样的应力-应变曲线、侧向扩容特征、变形模量和破坏裂纹发展规律的影响,并将高陡边坡在各种工况下的开挖进行数值模拟,用卸荷力学理论对岩体参数进行劣化,与监测结果对比分析。
现有研究中对于卸荷应力路径的研究虽然很多,但大多是基于恒轴压卸围压、恒围压加轴压的三轴试验,较少考虑卸围压加轴压以及卸围压卸轴压应力路径对岩石(岩体)力学性质的影响。在进行岩石卸荷试验的研究时,在不同的初始围压下,需考虑岩石不同应力路径、不同速率分段连续卸荷下岩石的力学特性、力学参数,变形模量以及破坏特征。对不同卸荷速率的研究,虽然在不同卸荷速率下进行了多个三轴卸围压试验,并进行了对比分析,得出了相关结论,但并未结合实际情况考虑人工操作和开挖方法的影响。实际工程中,边坡开挖卸荷的速率极有可能是分段连续变化的,在室内试验时应考虑这个因素的影响。为此,本文从卸围压卸轴压、卸围压增轴压、卸围压恒轴压3种不同应力路径出发,通过在试验中控制不同卸荷速率,模拟分段变速连续卸荷状态,探讨在不同的3种路径下砂岩的弹性模量、变形模量的变化特征。
1 试验方案及试样制取
试验岩石为选自四川西南地区某高陡边坡的长石砂岩,灰色,主要成分为石英(>52%)、粘土(约15%)、针铁矿(约18%)以及其他物质(约10%)。通过现场采样,选取完整、均匀的较大岩块,切割成小块运回试验室钻芯取样,按照DLT 5368—2007《水利水电工程岩石试验规程》[11]和国际岩石力学学会试验方法委员会《关于节理岩体大尺寸取样及三轴试验的建议方法》[12],岩样尺寸为直径50 mm或54 mm(与现场取得岩芯的方法有关)、长度为直径2~3倍的圆柱体。
为使试验结果更接近理论值,最大限度地消除误差,对岩样的制作、选取尤为苛刻,保证在层理一致、质地均匀的岩块上进行取样,并通过超声波测速的方法,对岩样进行筛选,最终选择了40个岩样。按照推荐标准,制成尺寸φ50 mm×100 mm圆柱形试件,见图1。

图1 试验试样
岩样分2组进行,先按每个工况下1个岩样为第1组进行试验,然后采用同样试验方案进行第2组,最后取2组数据的平均值作为最终试验数据。对于数值偏差较大的数据,用剩下的岩样作为补充试样,重新按相应试验方案进行后,对获取数据筛选,最大限度降低试验数据误差。试验中,将整个卸荷过程以30 s为间隔分成3个试验时间段;每个试验时间段卸荷速率都不相同;每个试验时间段持续30 s,且每个试验时间段卸荷是连续的,无间断。试验方案见表1。

表1 不同应力路径下分段变速连续卸荷试验方案
2 试验结果及分析
2.1 砂岩三轴压缩试验强度及变形参数
砂岩在5、10、15 MPa和20 MPa这4个围压等级下的偏应力-应变曲线见图2。试验中,三轴峰值应力σ1是三轴抗压强度与岩样底面积之比值;弹性模量通过偏应力-应变曲线中弹性变形阶段的直线斜率确定;而变形模量通过应力峰值的50%与应变比值,即割线斜率确定。砂岩三轴压缩试验强度及变形参数见表2。

图2 试样偏应力-应变的关系
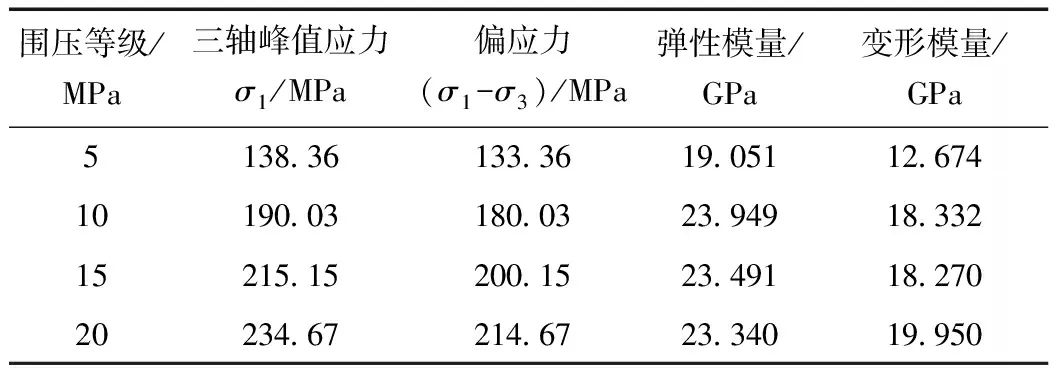
表2 砂岩三轴压缩试验及变形参数
2.2 不同应力路径下分段变速卸荷砂岩弹性模量
不同应力路径下分段变速卸荷的砂岩,在不同初始围压等级下弹性模量与变形模量见表3。从表3可知,任意应力路径下变形模量值都比弹性模量要小,且相同初始围压下,卸围压增轴压应力路径下的弹性模量与变形模量最大。
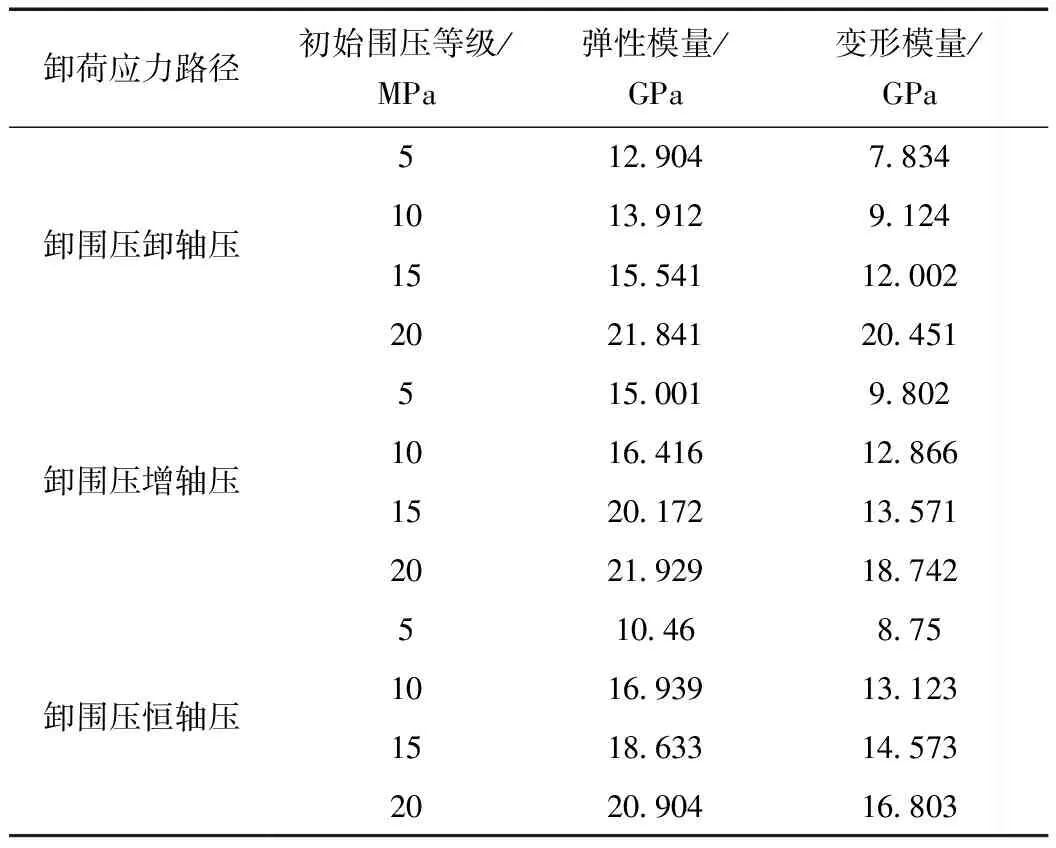
表3 基于不同应力路径下砂岩分段变速卸荷变形参数
结合表3中不同应力路径下砂岩的弹性模量与初始围压的关系,绘制出了相应的趋势线,见图3。从图3可看出,3种应力路径下,弹性模量总体上随着初始围压的增大而增大。在低围压阶段,基于卸围压卸轴压应力路径下弹性模量增加的最慢,而基于卸围压恒轴压应力路径下弹性模量增加的最快;在高围压阶段,弹性模量随初始围压的变化趋势与低围压阶段相反。

图3 不同应力路径下砂岩弹性模量
对弹性模量进行线性拟合,结果见图4。从图4可知,卸围压恒轴压下的弹性模量线性拟合斜率最大,说明在卸围压恒轴压应力路径下,弹性模量随围压增加的最快,并且拟合的相关系数也较大。而卸围压增轴压下的弹性模量线性拟合斜率虽然最小,但相关系数最大,拟合度最好。虽然卸围压卸轴压应力路径下线性拟合公式的相关性最低,但其斜率却较大。说明3种应力路径下的线性拟合公式可以很好用于拟合弹性模量和初始围压之间的关系。

图4 不同应力路径下砂岩弹性模量拟合
2.3 不同应力路径下分段变速卸荷砂岩变形模量
为了进一步探究不同应力路径下岩样的变形特征随初始围压的变化规律,研究了变形模量与初始围压的关系。结合表3中不同应力路径下砂岩的变形模量与初始围压的关系,绘制出了相应的趋势线,见图5。从图5可知,3种应力路径下的变形模量随初始围压都呈增大趋势,但是增长的平均速率却大不相同。

图5 不同应力路径下砂岩变形模量
对变形模量进行了线性拟合,结果见图6。从图6可知,不同应力路径下拟合的斜率各不相同,卸围压卸轴压斜率最大,卸围压增轴压其次,卸围压恒轴压最小。卸围压卸轴压下,变形模量线性拟合斜率最大,说明在卸围压卸轴压应力路径下,变形模量随初始围压增加的最快,并且拟合相关系数也较大,但与其他2种应力路径相比,其相关系数最小。卸围压恒轴压拟合的相关系数最大,但其变形模量拟合斜率却最小。通过此现象可发现,3种应力路径中变形模量的线性拟合斜率从上到下逐渐减小,但相关系数却逐渐增大。与变形模量不同的是,弹性模量线性拟合斜率在卸围压恒轴压下最大,而在卸围压卸轴压下最小,说明变形模量线性拟合斜率的变化规律和弹性模量线性拟合斜率的变化规律恰好相反。

图6 不同应力路径下砂岩变形模量拟合
2.4 不同应力路径下分段变速卸荷砂岩变形模量与卸荷当量的关系
以上研究了加载阶段,变形模量随初始围压的变化规律,但在岩样卸荷阶段,变形模量随卸荷围压的变化规律却大不相同,随着卸荷围压的减小,变形模量在不断变化。通过求卸荷当量Δσ3,可直观地研究卸围当量与变形模量之间的关系。计算公式如下
(1)

不同卸荷当量下砂岩变形模量统计见表4。岩样的变形模量随卸围压量的变化见图7。从表4和图7可知,每种应力路径下岩样的变形模量随初始围压的升高而增大,随卸荷当量的增加而减小。卸荷当量在0~60%之间时,变形模量基本都随卸荷当量线性下降,且速率较小,降幅一般都在0~5%之间;卸荷当量在60%~100%之间时,变形模量降幅突然变大且下降速率较大,说明岩样在临近破坏时,围压的微小变化便会引起变形模量的剧减。

表4 不同卸荷当量下砂岩变形模量统计

图7 不同应力路径下砂岩变形模量
3 结 语
本文基于室内三轴加载试验以及卸围压卸轴压、卸围压恒轴压、卸围压增轴压3种应力路径下的分段变速卸荷试验,研究高陡边坡岩体开挖卸荷过程中的变形问题,得出了以下结论:
(1)在每种应力路径下,岩样分段变速卸荷的弹性模量与变形模量都随初始围压的升高而增大,变形模量随卸荷当量的增加而减小。对比发现,任意应力路径下变形模量值都比弹性模量要小,且相同初始围压下,卸围压增轴压应力路径下的弹性模
量与变形模量相对较大。
(2)不同初始围压的变形模量随卸荷当量的降幅随着初始围压的增大呈减小趋势。每种不同应力路径下,变形模量降幅各不相同,基于卸围压恒轴压应力路径下的变形模量整体降幅最大,而卸围压增轴压下的变形模量降幅最小,说明卸围压恒轴压应力路径对于砂岩变形影响最为显著,卸围压卸轴压次之,而卸围压增轴压的影响最小。

