基于BP神经网络的膨胀土判别分级方法研究

杨娱琦，朱 晟

(1.河海大学水文水资源与水利水电工程科学国家重点实验室，江苏 南京 210024；2.河海大学水利水电学院，江苏 南京 210024)

0 引 言

膨胀土广泛分布于我国云南、贵州、四川、广西、河北、河南、湖北、陕西、安徽和江苏等地[1-2]。作为一种特殊土，膨胀土在塑性图上的分类属于高液限粘土[3]，具有一般粘土吸水膨胀、失水收缩的胀缩特性。膨胀土的特殊性在于其含有大量的蒙脱石、伊利石、高岭石等亲水粘土矿物，从而对于环境变化，特别是湿热变化非常敏感，体现在吸水时产生膨胀压力或失水时产生收缩裂缝。这种特性导致了膨胀土地区存在路基沉陷和开裂、边坡滑塌等严重威胁施工与运营安全的问题，也直接威胁了以膨胀土为地基的建筑物的安全性，可能造成建筑物开裂。同时，膨胀土在天然状态下一般强度较高、承载力较高、压缩性低，易被误认为是性质较好的粘土。考虑到这些工程问题，在有膨胀土分布的地区开展工程建设前，为有效预防和处理膨胀土可能带来的危害，首先必须将膨胀土同其他粘土区分开，其次对膨胀土进行膨胀潜势或胀缩性的分级，最后根据分级结果采取适宜的工程措施。若对膨胀土的胀缩性估计过高则将造成浪费，过低则会埋下安全隐患。因此，有必要建立可靠且便捷的膨胀土判别分级方法。

1 膨胀土判别分级方法研究现状

为了对膨胀土进行判别分级，进而定量划分其胀缩特性，国内外学者开展了大量研究工作，提出了不同的方法。美国垦务局Holtz等[4]以胶粒含量、塑性指数、缩限和膨胀体变为指标，提出了USBR方法；南非Williams等[5]根据塑性指数和小于2 μm粘粒含量建立了粘土膨胀势判别分级图；柯尊敬[6]、谭罗荣[7]分别把胀缩潜量和风干含水量作为膨胀土判别分级的的指标；姚海林等[8-9]对膨胀土的标准吸湿含水率进行了研究，发现其与膨胀土的蒙脱石含量、阳离子交换量、比表面积等指标有较好的线性关系，建议采用自由膨胀率、塑性指数和标准吸湿含水率这3项指标作为膨胀土的分级依据。

可见，膨胀土判别分级问题较为复杂，不同方法选取的指标和标准各不相同。这些指标可分为2类：第1类和膨胀土的物质组成有关，如粘粒含量、粉粒含量、蒙脱石含量、阳离子交换量等；第2类和膨胀土在与水相互作用中所体现的性质有关，如液限、塑限、塑性指数、自由膨胀率、标准吸湿含水率等。膨胀土性质十分复杂，其胀缩特性既受其物质组成控制，又和其微观结构密切相关。这些指标中的任何一项都只能代表膨胀土某一方面的特性，仅靠单一指标无法较为全面地反映其特性，故应采用多指标联合判定方法。判定指标的选取应尽可能满足以下几条原则：①反映膨胀土特有物理力学特性；②测量较为简单方便；③受环境变化影响小，重现性好；④各指标间独立性好。

目前对于膨胀土的判别分级方法，国内相关标准尚未有统一的指标选取：①GBJ 145—90《土的分类标准》(以下简称“标准1”)[10]提出根据塑性图对膨胀土进行初步判断。②JTG D30—2004《公路路基设计规范》(以下简称“规范1”)[11]在条文说明中初步提出了依据自由膨胀率、塑性指数和标准吸湿含水率对膨胀土进行判别分级的方法，且给出了膨胀潜势分级的参考标准。③ GB/T 50145—2007《土的工程分类标准》(以下简称“标准2)”[12]明确废止了标准1，仅在条文说明中指出膨胀土应依据相应的技术标准进行分类。④JTG C20—2011《公路工程地质勘察规范》(以下简称“规范2)”[13]明确提出了膨胀土的自由膨胀率、塑性指数和标准吸湿含水率三指标分级方法(见表1)。⑤GB 50112—2013《膨胀土地区建筑技术规范》(以下简称“规范3)”[14]仅给出自由膨胀率作为膨胀潜势分级判据。⑥JTG D30—2015《公路路基设计规范》(以下简称“规范4”)[15]指出膨胀土的标准吸湿含水率不小于2.5%，膨胀土判别和膨胀潜势分级应符合规范2的有关规定；在条文说明中指出规范3的自由膨胀率判别法的可靠性存在争议，易产生误判和漏判。⑦TB 10077—2019《铁路工程岩土分类标准》(以下简称“标准3”)[16]规定膨胀土按照自由膨胀率、蒙脱石含量和阳离子交换量进行分级(见表2)。

表1 膨胀土分级标准(公路)

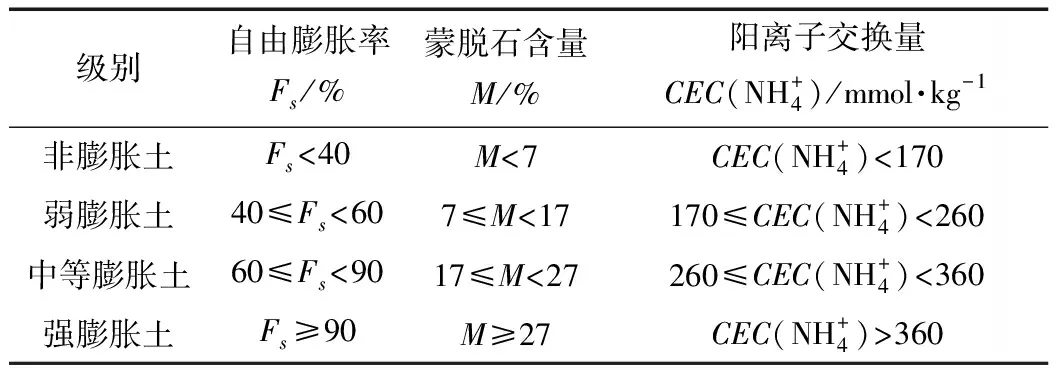
表2 膨胀土分级标准(铁路)

可见，膨胀土的相关标准目前没有统一分级方法，公路和铁路部门的分级指标不同。公路部门采用的3个指标测试难度相对较小，但属于同一类指标，未能直接体现膨胀土的物质组成。铁路部门同时采用了2类指标，且蒙脱石含量和阳离子交换量能够反映膨胀土的本质，但这2个指标测试困难，难以推广。

实际使用指标分级法时，对某一膨胀土试样，会出现按不同指标分级而结果不一致的现象，即可能跨越2个、甚至3个级别，这样得到的分级结果显然存在争议。不难发现，规范4和标准3分级界限值的选取对膨胀土的分级结果影响显著。段海澎等[17]依托皖中地区合肥—六安—叶集高速公路，应用规范1对沿线广泛分布的膨胀土进行的判别分级研究发现，规范1推荐的分级标准不适用于皖中地区膨胀土，并给出了建议的膨胀潜势分级标准，具有较好的适用性和准确性。因此，膨胀土的分级必须考虑其地域性。统一的定量分级标准存在局限性，而若是定性描述则难以得到一致的结果。

考虑到这一问题，有必要对膨胀土的判别分级开展进一步研究。近年来，学者们在以往指标分级法的研究基础上，结合不同的数学工具，提出了相应的膨胀土分级方法，如模糊数学法[18-19]、支持向量机法[20]、Fisher判别分析法[21]、云模型法[22-23]等。这些方法为膨胀土判别分级问题提供了新的思路，但也存在一些问题，难以客观准确地进行分级指标权重的赋值；选用的分级指标测试难度较大，不利于工程实用。

近年来，人工神经网络迅速发展并得到了广泛应用。易顺民[24]、刘书贤[25]等利用神经网络方法对膨胀土分级进行了初步研究，但缺乏系统性且未分析各指标对分级结果的影响。为此，本文以安康地区膨胀土为研究对象，选用粘粒含量、粉粒含量、液限和塑性指数作为分级指标，建立两层无偏置的BP神经网络模型，对安康膨胀土开展了判别分级的学习与预测，并进行了各指标的敏感性分析。

2 基于BP神经网络的膨胀土判别分级方法

2.1 BP神经网络基本原理

1986年，以Rumelhart和McClelland为首的科学家提出了BP神经网络的概念，这是一种按照误差反向传播算法训练的多层前馈神经网络，其学习过程由信号的正向传播与误差的反向传播2个过程组成。正向传播时，信号由输入层传入，经隐含层逐层处理后传向输出层。反向传播时，根据输出层输出值与期望值之间的误差，利用梯度下降法反向逐层修正各神经元连接的权值和偏置。如此反复迭代，直到误差满足一定的停止条件，利用学习好的神经网络，即可对未知样本进行预测。BP神经网络无需在输入量与输出量之间建立确定性的数学关系、具有良好的自适应性且能够用于对输入信号的分类，理论上可用于膨胀土的判别分级。

2.2 判别指标选取

基于指标选取原则，首先考虑到利用塑性图可以对膨胀土进行初步的判别，故在上述第2类指标中选取液限指数和塑性指数2个指标；其次选取的指标既能体现膨胀土与水相互作用中表现的性质，又能反映其物质组成，在第1类指标中宜选取2个。为降低测试难度，便于应用推广，选取粘粒含量和粉粒含量。因此，本文选取的判别指标为粘粒含量、粉粒含量、液限指数和塑性指数4个指标。

2.3 BP神经网络模型建立

神经网络设输入层、隐含层和输出层。输入层4个神经元x1、x2、x3、x4，分别代表4个判别指标粘粒含量、粉粒含量、液限、塑性指数。将膨胀土分级结果分为3类：强膨胀土、中膨胀土和弱膨胀土，分别对应输出层的3个神经元y1、y2、y3。输出层的值为1个1×3的矩阵y=[y1，y2，y3]，其中，[1，0，0]表示强膨胀土，[0，1，0]表示中膨胀土，[0，0，1]表示弱膨胀土。隐含层设定为5个神经元。据此，本文建立了模型结构如图1所示4×5×3的两层无偏置BP神经网络模型。以安康地区膨胀土[24]为例进行研究，该BP神经网络模型学习过程的算法步骤如下：

表4 模型学习结果

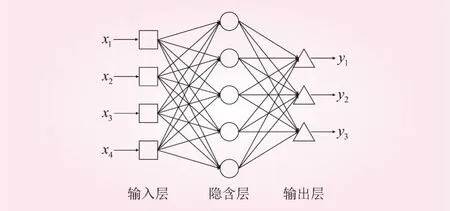
图1 BP神经网络模型结构示意

(1)给定学习集D=(xk，yk)，其中xk、yk分别表示输入值和期望输出值。设定隐含层和输出层的激活函数f(x)，给定学习率η、停止条件。在[-1，1]之间随机生成输入层第i个神经元与隐含层第h个神经元之间的初始权值vih、隐含层第h个神经元与输出层第j个神经元之间的初始权值whj，即权值矩阵V、W。激活函数取为Sigmoid函数，即

(1)

(3)计算误差。若算得误差不满足停止条件则继续步骤(4)，若满足则继续步骤(6)。其中，误差取均方误差，即

(2)

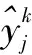
(4)根据梯度下降法，以目标的负梯度方向更新各层之间的权值，其中

(3)

(4)

(5)

(5)根据更新的网络计算得到输出值，回到步骤(3)。

(6)学习结束。根据学习好的神经网络模型，即可对未知样本进行预测。

2.4 确定学习率 η

为了利用学习好的模型对未知样本进行预测，要求学习时能够尽快收敛。当学习集的输入值和期望输出值、权值矩阵的初始值和各神经元的激活函数一定时，学习率η控制着每轮迭代的更新步长，若太大则可能震荡，无法收敛，太小则收敛速度过慢，降低计算效率，因此需要确定合理的学习率η。为此，选取文献[24]中17个实测安康地区膨胀土样本作为学习集，η分别取1、0.5、0.25和0.125，迭代20 000次。学习结果见图2。不同学习率误差统计见表3。根据图2和表3，对不同学习率模型均能较快收敛，学习效果良好，误差小。当学习次数小于10 000次时，学习率越小，收敛速度越慢。当学习次数为20 000次、学习率为0.5时误差最小。因此，

表3 不同学习率误差统计

图2 学习结果

对于本模型，学习率η可在0.125～1的范围内取值。设定学习率η为0.5，停止条件为误差Ek≤1.0×10-7。

2.5 安康膨胀土学习与预测结果

模型学习结果见表4。输入层到隐含层、隐含层到输出层的权值矩阵V、W分别为

利用学习好的神经网络对6个未知样本进行预测，结果见表5。根据表4、5可知，本文选取的BP神经网络经过学习后，对未知样本的预测结果与实际结果完全吻合，因此该模型能够用于安康膨胀土的分级。

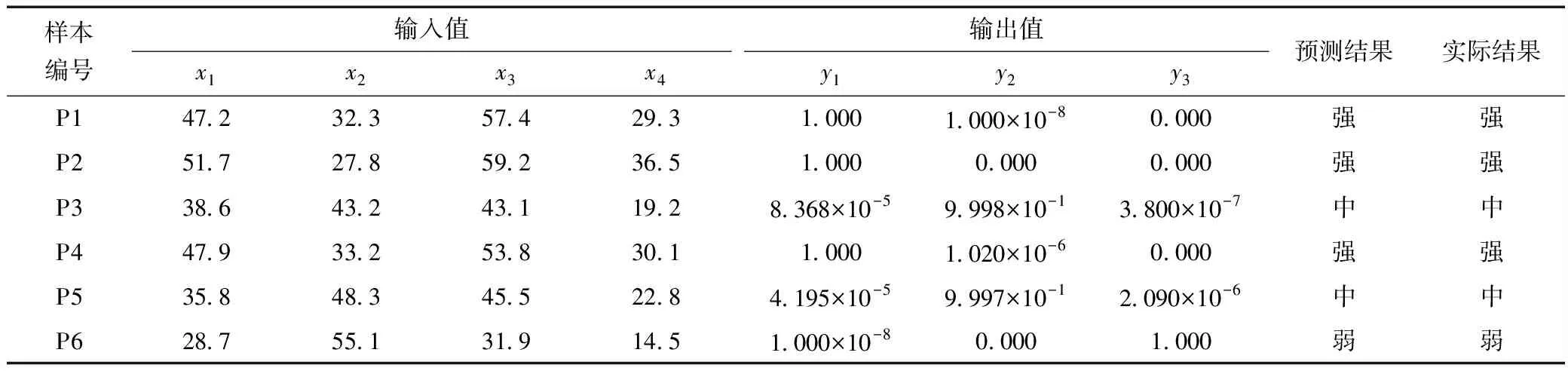
表5 模型预测结果

3 指标敏感性分析

本文选取的判别指标均需要通过试验测得，存在测量误差。对于传统的指标分级法，若指标测量值在分级界限值附近，则测量误差可能导致误判。神经网络方法具有一定的容错能力，可以有效减小测量误差对结果的影响，下面结合本文建立的模型具体说明。

对6个未知样本的各输入变量分别加±2%、±4%、±6%、±8%和±10%的扰动，共计240个样本，利用本文模型进行预测。所有扰动样本中，最终有10个产生了误判，误判样本结果见表6。对各指标扰动后模型预测误差进行统计，结果见表7。从表6、7可以看出，当各指标扰动量不超过4%时，均不会对预测结果产生影响。

表6 误判样本结果

表7 各指标扰动后模型预测误差统计

对于粘粒含量和粉粒含量，绘制不同扰动量下模型预测误差与误判数，见图3。从图3可知，当粘粒含量逐渐减少或粉粒含量逐渐增加时，预测误差逐渐增大，直至对P1和P4样本产生了由强膨胀土到中膨胀土的误判。进一步分析可知，不论是粘粒含量的减少，还是粉粒含量的增加，都会导致样本蒙脱石等亲水粘土矿物含量的减少，从而其膨胀性随之降低。

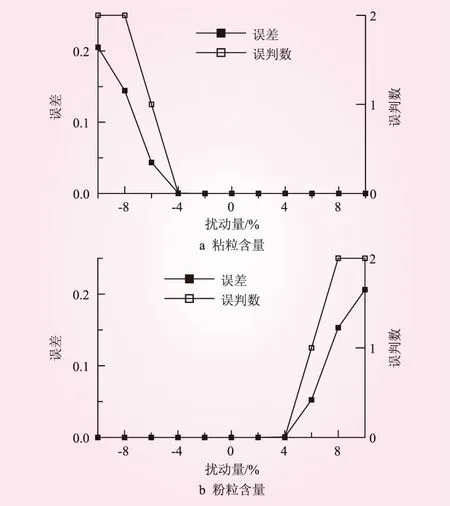
图3 不同指标扰动后模型预测误差与误判数

液限和塑性指数即使有10%的误差，也未对预测结果造成误判。观察权值矩阵V的各元素可知，相比于第1、2行，第3、4行的元素绝对值较小，则液限和塑性指数对输出值的影响较小，故这2个指标的扰动对判断结果影响较小。

综上，本文模型选取的4个指标中，粘粒含量和粉粒含量的测量精度对预测结果影响较大，而液限和塑性指数的影响较小；同时，对于这4个指标的测量，液限和塑性指数的测量误差较大，经敏感性分析，这2个指标的扰动对判别影响较小。因此，本文模型能有效减小指标测量误差对预测结果的影响，具有较好的容错能力。

4 结 语

本文以安康膨胀土为研究对象，选用粘粒含量、粉粒含量、液限和塑性指数4个分级指标，建立了两层无偏置的BP神经网络模型，对安康膨胀土进行了判别分级研究，得到如下结论：

(1)本文建立的模型选取的指标测试相对简单，学习效果良好，能够准确预测未知样本的膨胀性。

(2)对于安康膨胀土，粘粒含量和粉粒含量对分级结果影响较大，而液限和塑性指数影响较小。

(3)相比于传统的指标分级法，本文模型具有较好的容错能力，可有效减小指标测量误差对分级结果的影响。

(4)BP神经网络用于膨胀土的判别分级是合理可行的，具有一定的推广与应用价值。