基于Hotbooting-Q算法的抽水蓄能电网电能交易风险识别方法

王荣茂，刘 淼，李青春，张 晔

(辽宁电力交易中心有限公司，辽宁 沈阳 110006)

0 引 言

利用热启动Hotbooting技术融合Q-Learning算法(以下简称Q学习算法)构成Hotbooting-Q交易算法[1]。通过Hotbooting技术得到类似场景下Q学习算法的Q值表及V值表，其中，Q值及V值是Hotbooting-Q交易算法在强化学习中的定义值，其在较大程度上缩减该算法的学习步长，提升收敛性能的同时获取优良学习效果[2-3]。

电能交易需求猛增，电网企业的业务压力也随之增强。近年来，国家高度重视抽水蓄能发电，作为发展新型能源的关键组成部分，其优势在于可靠性高、技术发展成熟、生命周期久，抽水蓄能电站可提升电网运行的平稳性及协调能力，节能减排、低碳环保、促进可再生能源发展是我国对新兴能源的基本要求，实现资源优化配置[4]，关乎社会、经济、文明发展，对电力储能具有重要意义。电网电能在频繁交易过程中可能存在风险，对风险的识别显得格外重要，及时发现并规避风险，保证电能交易安全可靠运行，关乎民生经济等各个方面的安全运行。陈涛等[5]提出抽水蓄能水电站职业健康风险评价方法，在模糊数学法基础上进行风险评估，该方法成本较高不适宜全面推广使用；李刚等[6]提出抽水蓄能电站水淹风险评价研究方法。

综合以往研究方法，本文提出基于Hotbooting-Q算法的抽水蓄能电网电能交易风险识别方法，及时发现并规避风险。

1 基于Hotbooting- Q算法的抽水蓄能电网电能交易策略

1.1 基于深度Q学习算法的电网电能交易模型

抽水蓄能电网DWi和上级电网、其他抽水蓄能电网进行电能交易，对下一时期电能存储值和其他抽水蓄能电网交易决策有直接影响，因此，利用马尔科夫过程表示抽水蓄能电网电能交易博弈机制[7]，在动态博弈过程中，其他抽水蓄能电网的电量程度和抽水蓄能电网本身负荷需求无法得知的情况下，采用深度Q学习算法进行计算，获取满足切身利益的电能交易策略[8]。

DWi瞬时效益函数为

(1)

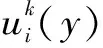
DWi依据本身实际情况的交易策略对Q函数实施同步更新的过程表示为

(2)

(3)

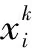
(4)

(5)

至此，完成基于深度Q学习算法的抽水蓄能电网电能交易博弈模型构建。

1.2 深度Q学习算法中Hotbooting技术的运用

处于初始化Q值表时，深度Q学习算法将全部元素设为0，历次学习时从0开展大规模探寻并训练，在较大程度上提升学习速度。将深度Q学习算法与Hotbooting技术二者融合，能够大幅减少实践操练时间并快速提升该算法的收敛性能[10]。

依据之前电能交易类似情景在类似情况下进行模拟实验，并获取实践操练数据，在此基础上，对Q值表、V值表开展初始化处理[11]，该过程采用Hotbooting技术完成，利用处理后的Q值表及V值表取替初始化值表。该模型求解流程如下：

(3)合法交易值采用挑选整理数据的方式获取。

(5)实时上报交易策略，同时更新电能值得到下一阶段状况。

(6)模仿交易环境需利用Hotbooting技术完成，得到结果Q值表及V值表。

(7)深层次Q学习算法交易控制中心调整交易策略，得到最优预期效益。

图1为完整的模型求解流程。

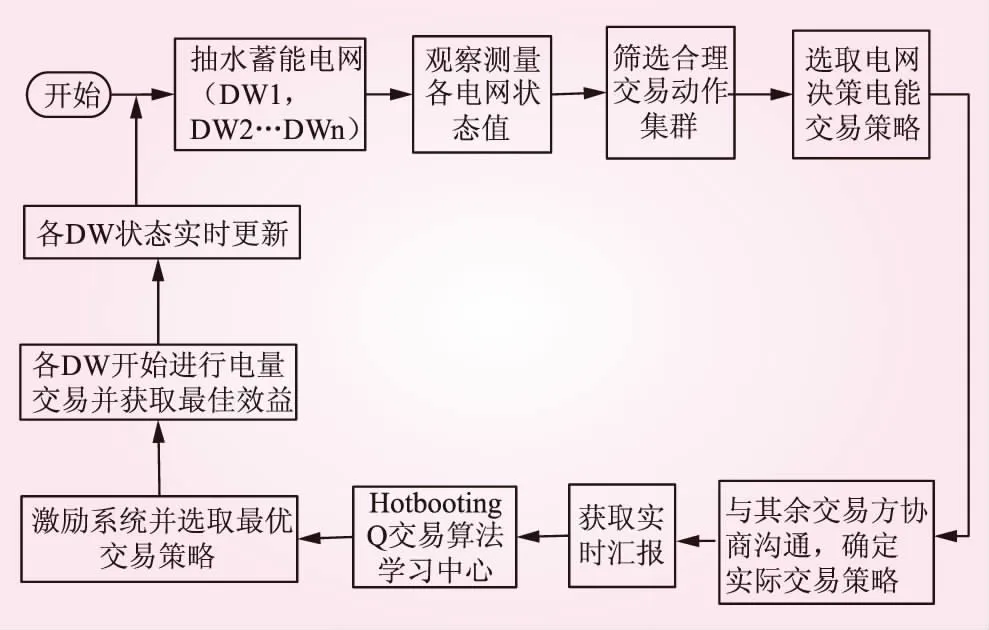
图1 求解流程

2 抽水蓄能电网电能交易风险识别模型

2.1 搭建风险识别网络拓扑结构

拟设一个抽水蓄能电网电能网络拓扑及交易拓扑，用G=(N，E)表示电网电能网络。N、E分别为网络节点合集和网络中无向边合集；网络拓扑中第c条边用Ec表示。Gs=(Ns，Es，S)为电网电能网络拓扑。其中，用下角标s表示交易拓扑，有交易经过的网络节点合集和网络中有交易经过的边合集分别用Ns、Es表示，同时用Es(c，f)表示网络中有交易经过连接节点c和f的边；网络的交易合集用S表示，经过网络中Es(c，f)边的交易合集用SE(c，f)表示。网络中第c个交易重要度的数值用Isc表示。Ns={N1，N2，…N6}表示网络节点合集，用Es={E1，E2，E3，E4，E5，E7}表示网络负载交易的边合集，其中，两条边E6，E8为不负载交易且不包含在Es内，用S={S1，S2，S3，S4，S5}表示全部交易的合集。

2.2 交易重要度分析

交易业务突发中止或出现交易缺陷情况时对电网平稳运转产生的影响水平为交易重要度，该指标用于评估抽水蓄能电网电能交易对电网影响的重要程度[12-13]。

2.3 交易风险均衡度测度指标及算法

2.3.1 交易风险度

电网平稳运转受到交易中止或者交易牢靠性减弱时的影响水平为交易风险度[14]，采用最优交易策略的电网通信网络通道段所负载的单一交易的风险程度表示为

R(Es(c，f)sc)=Isc(I-PEs(c，f))·A

(6)

式中，R(Es(c，f)sc)为第Es(c，f)边负载的sc交易的风险值；Isc为网络中第Es(c，f)边上负载的第c笔交易重要度；PEs(c，f)为网络中负载第c笔交易第Es(c，f)边的牢靠度数值；A为牢靠性减弱时的影响水平调节系数。

网络负载交易的某一通道段为通道段综合交易风险度，即网络中对应边负载的各个交易风险度综合值[15]。Es(c，f)边负载的Sc交易的风险值总和为R(Es(c，f))，其公式为

(7)

式中，网络中边Es(c，f)负载的各类交易各类别数目和第c类交易数目分别为m和Nc。

2.3.2 交易风险均衡度

2.3.2.1 全网交易风险度总和

设全网交易风险度为R(Gs)，鉴于交易具有双向性，同一个网络边的交易风险值分别用REs(c,f)、REs(f,c)表示，R(Gs)可表示为

(8)

求解R(Gs)的第一步为求和Es(c，f)边负载交易的风险度值，第二步为求和归属于交易网络Gs全部边交易风险度值。

2.3.2.2 全网平均交易风险度

依据全网交易风险度及网络拓扑中边的数目N，计算得到全网平均交易风险度。

2.3.2.3 网络交易风险均衡度

电网电能交易风险均衡度模型为

(9)

采用全网交易风险度均衡度BR(Gs)衡量网络整体交易分配均衡性，将基于深度Q学习算法的抽水蓄能电网电能交易博弈模型获取的最优交易策略作为模型输入，对抽水蓄能电网电能交易过程中可能存在的风险进行识别，掌控电网电能交易状态。分别从交易风险分布均衡度和风险度两方向进行分析，网络中各项交易通道段负载的交易风险度平衡分散状态依据交易风险均衡度指标进行衡量，当指标接近0时代表全网的交易安排风险处于平衡状态，此时运行风险较小；当指标过大时则代表网络中交易通道上负载的交易分散失衡，其中部分链重要交易过度聚集或过度轻载。

2.3.3 识别编码

2.3.3.1 网络节点交易连接矩阵编码

考虑到节点间邻接关系和交易连接关系，节点间交易状态矩阵S(Gs)表示为

(10)

元素S(Gs)cf位于节点交易连接矩阵S(Gs)中，该元素等量互换为SEs(c，f)，代表节点c和f当中的边的交易连接状况。当两个节点发生交易连接时，S(Gs)cf=1；无交易连接时，S(Gs)cf=0(c≠f)；其中节点本身无交易关联关系用S(Gs)cf=0表示。

2.3.3.2 交易重要度矩阵编码

电网通信网负载多类电网通信交易，设种类为M，M种电网通信交易重要度M×1阶的矩阵形式为

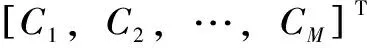
(11)

2.3.3.3 网络多边交易重要度计算

边Es(c，f)负载交易矩阵SEs(c，f)=[Sk1，Sk2，…，SkM]，电网通信交易类别用下角标M表示，边Es(c，f)负载第c类交易数目用Sk1表示。SEs(c，f)用于表示S(Gs)内部的某一元素。

IEs(c，f)用于表示网络中边负载的各项交易重要度之和，IEs(c，f)与各节点交易连接矩阵和交易重要度矩阵、边交易矩阵之间的关联关系等同于交易重要度矩阵C、S(Gs)内部的某一元素SEs(c，f)和节点交易连接矩阵S(Gs)中的S(Gs)cf元素三者乘积。

2.3.3.4 全网交易重要度计算

依据各节点的交易连接关系将全网交易的重要度分布矩阵表示为

(12)

式中，I(Gs)的矩阵阶为n×n，网络节点数目用于表示n，任意两个节点间各类交易的重要度之和用于表示中I(Gs)的每个元素。

求解全网交易风险度

R(Gs)=I(Gs)P(Gs)

(13)

若不考量其他因素，单一考量风险及交易重要度的关系，用R(Gs)=I(Gs)表示R(Gs)的矩阵形式，利用网络多边交易重要度求取IEs(c，f)。

全网负载交易的各边风险度之和为

(14)

采用全网平均交易风险度及网络交易风险均衡度指标，对全网交易平均风险度即风险均衡度进行求解。

网络中第c个节点Nc交易风险度为

(15)

至此，完成抽水蓄能电网电能交易风险识别方法设计。

3 实验分析

采用MATLAB编程软件搭建某区域的抽水蓄能电网，应用本文方法对该电网的电能交易风险进行识别，利用本文方法与文献[5]抽水蓄能水电站职业健康风险评价方法、文献[6]抽水蓄能电站水淹风险评价方法进行对比验证，验证本文方法的识别效果。

在该电网中，选取一个5节点、7边的抽水蓄能区域电网，该区域网络节点合集为Ns={N1，N2，N3，N4，N5}，网络负载交易边合集为Es={E1，E2，E3，E4，E5，E6}，网络负载交易合集为S={S1，S2，S3，S4，S5}。采用本文方法获取该区域电网交易的最优预期效益，并从交易重要度及交易风险度、交易风险均衡度、识别编码方面进行分析，并搭建电网电能交易风险均衡度的识别模型，进行交易风险识别。

利用式(15)遍历某市抽水蓄能电网电能交易过程中的各个节点，并识别得到该电网电能交易风险度结果如表1所示。

表1 各节点交易风险均衡度结果

由此可见，本文方法能够有效识别出各电网电能交易节点风险度值。

为分析电能交易后，该电网的平均效益水平曲线，将学习布长设为6 000步，利用本文方法与文献[5]方法、文献[6]方法进行对比验证，效益变化曲线如图2所示。

图2 效益变化曲线

根据图2可知，在收敛性方面，本文方法和文献[5]方法在初步时有一段较为鲜明的学习时间，且本文方法在500步左右完成收敛，比文献[5]提前完成，这是因为本文方法运用Hotbooting技术，预先对相似场景下的数据进行大批量的仿真测试，极大程度上缩短了后续学习的摸索时间，加速掌控交易规律；文献[6]方法并无学习过程且未能从交易数据中汲取经验和规律，效益值也最低，由此可见，本文方法能够提高交易效益，且整个算法的收敛性好。在收益情况方面，文献[6]方法交易策略的收益值较差，最高不超过8.9；文献[5]方法交易策略的收益值在14.5区间范围内浮动，与文献[6]方法相比提升约38.6%；本文方法的收益值平稳维持在18.5，较文献[5]、[6]方法分别提升约51.9%、21.6%。

对电网电能交易运行风险分析进行仿真模拟，随机选取该电网中的70条电网电能交易线路，依据电网电能交易状态风险信息传输路径，对不同数量交易线路的交易风险进行识别，将本文方法与文献[5]、文献[6]方法对比验证，判定识别精度更高的方法。用图3表示3种方法识别不同数量线路的风险识别失误次数。

图3 风险识别失误次数

由图3分析可知，文献[5]方法在交易线路数量为30次以内时风险识别失误在9次左右浮动，交易线路数量超过30次后其失误次数呈直线上升状态，风险识别失误次数全程在8～18区间内，识别效果较不理想；文献[6]方法风险识别失误次数全程在12次以上，随着交易线路数量逐步上升，交易风险识别监督逐渐降低；本文方法整体平稳运行，风险识别失误次数全程始终保持在3次以内，由此可见本文方法识别精度极高且稳定，可放心投入运行使用。

4 结 论

通过搭建基于Hotbooting-Q算法的抽水蓄能电网电能交易模型并求解获取最佳交易策略，将交易策略输入风险识别模型求解风险度，以此判断风险高低，在步长500步时完成收敛，其收益值平稳维持在18.5，高效且平稳；风险识别失误次数全程始终保持在3次以内，交易风险精准度极高，可有效识别出交易风险。