考虑堆石料空间变异性的心墙坝地震安全性随机有限元分析

杨 鸽，朱 晟，D. V. Griffiths

(1.杭州国家水电站大坝安全和应急工程技术中心有限公司，浙江 杭州 311122； 2.中国电建华东勘测设计研究院有限公司，浙江 杭州 311122；3.河海大学水工结构研究所，江苏 南京 210098；4.科罗拉多矿业大学土木与环境工程学院，科罗拉多 戈尔登 81401)

中图分类号：TV641.41;TU435文献标识码：A文章编号：0559-9342(2022)01-0077- 08

0 引 言

土石坝由天然岩土材料堆筑而成，虽然国内外现行的施工填筑规范中都对堆石料的干密度以及表征其密实程度的指标给出了较明确的控制标准，但对堆石料的级配和母岩性质等因素的控制则相当“粗放”[1-3]。不少研究都证明[4- 6]，密实程度相同的同一种堆石料，其级配不同时力学性质也会有较大差别；而母岩特性对堆石料力学性质的影响更是无须赘言。因此，虽然土石坝施工过程中对筑坝堆石料进行了质量控制，但坝料的物理力学性质仍很可能具有一定的不确定性。

近年来，已有很多学者致力于探讨岩土材料的不确定性对结构反应影响的研究，例如Vanmarcke[7]、Baecher和Christian[8,9]、Griffiths和Fenton[10-16]、龚晓南和黄广龙等[17-19]、Duncan和Low[20, 21]、Popescu等[22-23]、傅旭东等[24-26]以及李典庆、蒋水华、祁小辉等[27-33]的一系列研究。然而，在土石坝抗震工程领域，只有吴再光等[34]、Sanchez Lizarraga[35]以及王笃波等[36]曾探讨筑坝材料的不确定性对大坝动力反应的影响。笔者曾探索采用随机有限元法(Random Finite Element Method， RFEM)对土石坝进行随机地震响应进行分析，并以某高混凝土面板堆石坝为例，探讨了堆石料的级配、Duncan-ChangE-B模型模量系数以及初始摩擦角等物理力学性质的空间变异性对大坝地震加速度响应及永久变形的影响[37]。

本文将以某高心墙堆石坝为例，进一步探讨筑坝材料的不确定性对心墙坝动力响应及抗震安全的影响。研究思路为在蒙特卡罗法的框架下，采用RFEM模拟考虑筑坝堆石料空间变异性时心墙坝的加速度响应及永久变形，通过对比随机有限元法和常规确定性有限元法的计算结果，讨论筑坝堆石料的空间变异性对心墙坝动力响应的影响，然后再对各随机物理性质参数的敏感性进行比较分析。

1 心墙坝地震安全性随机有限元分析方法

采用随机有限元法分析心墙坝加速度响应及永久变形的基本流程如图1所示。首先，采用局部平均细分法生成一组具有空间变异性的材料随机场；然后，采用“逐单元法”将材料随机场映射至有限元网格，使每个网格单元都找到相应的材料参数取值；之后，调用有限元静力分析模块，模拟坝体材料为该组随机场时坝体的应力、变形等；最后，输入地震动荷载，调用动力有限元分析模块，采用Wilson-θ法逐步求解动力平衡方程，计算每个小时步内的动力加速度响应以及动应力。在此基础上，采用沈珠江经验公式计算残余体应变和剪应变，利用初应变法计算残余变形。通过上述过程即完成了一次随机有限元分析，得到了一个随机样本，在蒙特卡罗法的框架下，重复上述步骤多次，直至计算得到的随机样本达到统计稳定后，即可通过对随机样本的统计分析，估计大坝地震响应的统计特性。

图1 随机有限元分析心墙坝随机地震反应的基本流程

局部平均细分法生成材料随机场的原理见文献[37]以及Fenton[38]和Vanmarcke[39]的研究。土石坝非线性静动力有限元分析的原理见顾淦臣等[40]的介绍。计算结果的统计稳定采用主要性能指标的滑动平均值(Running Average，Run.ava.)和滑动标准差(Running Standard Deviation，Run.sd.)判断，其具体定义见文献[37]。

2 案例概况

R工程初步设计挡水建筑物为砾石土直心墙堆石坝，最大坝高315 m，上游坝坡为1∶2.1，下游坝坡坡比为1∶2.0。心墙顺河向最大宽度为162 m，上、下游坡比均为0.23；心墙与上、下游坝壳堆石之间设反滤层、过渡层。

2.1 计算模型

采用如图2所示的有限元计算模型，共有4 595个实体单元，另在心墙与反滤I区之间设置124个接触面单元。静力分析模拟坝体的填筑和蓄水过程，坝体自重荷载的施加考虑施工填筑的顺序分34级施加；水荷载则分8级施加至正常蓄水位。动力荷载方面，根据工程场地地震安全性评价报告，场地100年超越概率2%的基岩地震加速度峰值为0.434g，典型场地地震动时程如图3a所示，对应场地加速度反应谱如图3b所示。

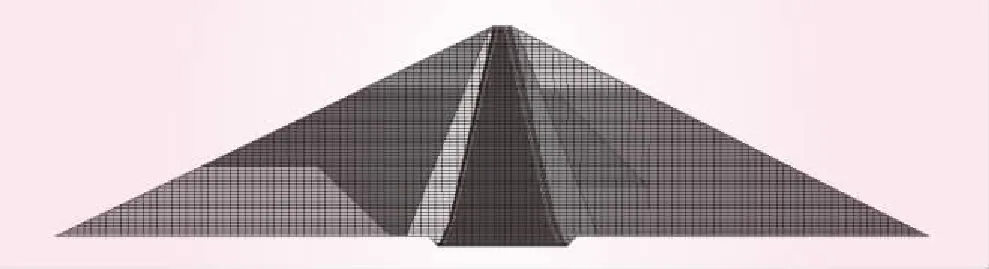
图2 有限元计算网格

图3 地震动输入(100年超越概率为2%)

2.2 堆石料的物理力学性质及其不确定性

筑坝堆石料的物理力学性质都具有一定程度的不确定性以及空间变异性。为了解堆石料力学性质(特别是变形特性)的不确定性，需要对大量的力学试验结果进行统计分析，成本极高。受此影响，目前对岩土材料不确定性的研究多集中在其物理性质上，只有少数研究涉及到了材料的强度特性和变形特性；而在考察材料不确定性对结构反应的影响的研究中，也一般只考虑材料物理性质或强度特性的不确定性，极少研究涉及到材料变形特性不确定性[38,41,42]。特别值得注意的是，在几乎所有考察岩土材料力学特性不确定性对结构反应影响的研究中，描述力学特性不确定性的统计参数都是作者根据有限的已发表的文献中的数据“拟定”而来，并非根据对具体研究对象的试验测量结果获得。

相比于力学性质参数，岩土材料物理性质参数的统计特性则通常较容易获得。为此，笔者提出[37]采用包含材料物理指标的力学模型描述筑坝岩土材料的力学性质，这样便可通过材料物理参数的统计特征推算出材料力学特性的统计特征，从而大大降低获取材料力学参数统计特性的成本，使岩土结构概率性分析中材料参数统计特性的获方法更加可靠。

2.2.1 动力本构模型

堆石料动力性质方面，将采用Menq[5]提出的包含堆石料孔隙比e、不均匀系数Cu、平均粒径D50的动本构模型，并将上述物理参数设置为具有空间变异性的随机场，即

(1)

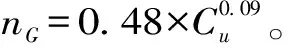
得到Gmax后，可通过下式计算动剪模量G，即

(2)

式中，γ为动剪应变；γr为参考应变，γr=K1×Cu-nr×(σ0/Pa)0.5，其中，nr、K1均为拟合参数；a为指数，a=K2+0.1×lg(σ0/Pa)，其中，K2为参数。

材料的阻尼特性方面，由于Menq给出的计算公式形式过于复杂，本文采用下式计算阻尼比：

(3)

式中，λr为参考阻尼比，λr=K3(σ0/Pa)+K4，其中，K3、K4均为拟合参数。

上述模型中，参数KG、nr、K1、K2、K3、K4需通过对材料动力试验曲线拟合得到。结合室内试验土料的物理指标，对R工程堆石料动力三轴试验结果进行拟合，得到Menq模型的拟合模型参数取值见表1。

表1 动力本构模型参数

2.2.2 静力本构模型

材料的静力本构模型方面，由于目前暂时尚未有描述堆石料物理指标与静应力-应变关系的模型，本文将继续沿用在心墙坝有限元分析中常用的Duncan-ChangE-B模型，并参考以往经验将对结构反应影响较大的参数(模量系数K和初始摩擦角φ0)设置为随机场。对R工程堆石料静三轴试验结果进行拟合，得到Duncan-ChangE-B模型参数见表2。

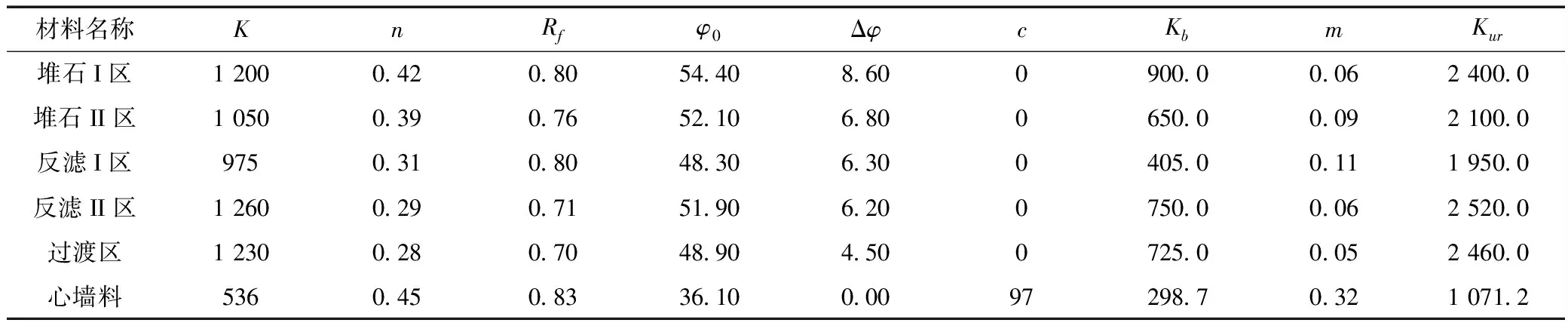
表2 静力本构模型(Duncan-Chang E-B模型)参数

此外，土体干密度决定了静力分析阶段的自重荷载以及动力分析阶段的惯性力，因而也被设置为随机场。

2.2.3 随机物理力学参数的统计特性

随机有限元分析中将考虑堆石料孔隙比e、不均匀系数Cu、平均粒径D50、干密度、E-B模型的模量系数以及初始摩擦角的空间变异性。由于示例工程尚未建成，并无法通过对坝体材料的检验确定上述随机变量的统计特性，因而本文将参考现有填筑标准、相似工程现场检测资料以及相关研究成果综合估计上述随机参数的统计特性，统计参数的具体拟定过程见文献[37]，拟定结果见表3。

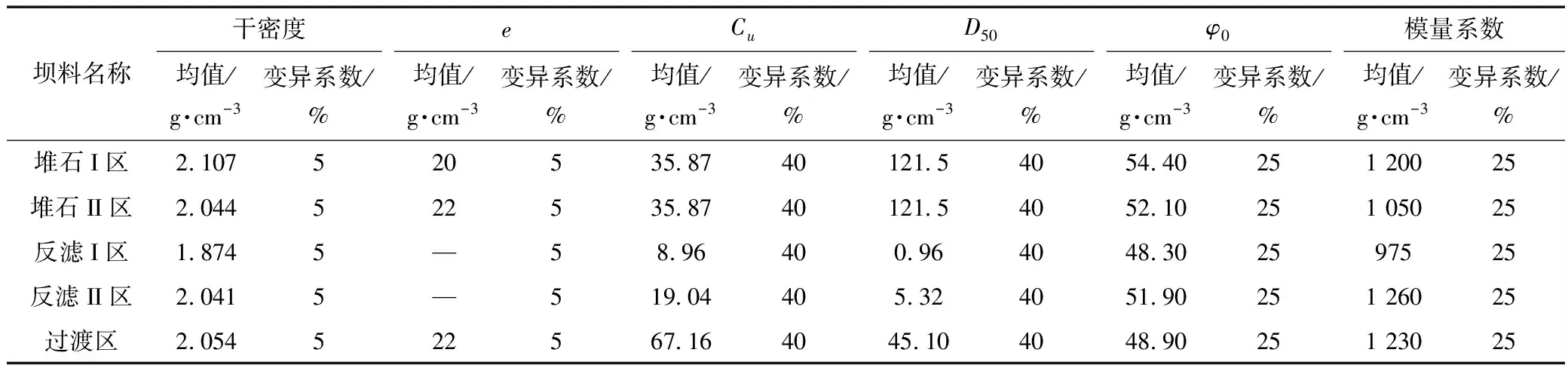
表3 堆石料物理参数

随机场内不同位置对应的变量间的相关性强弱用相关距离描述。目前仅有少量针对天然土层的相关距离的研究成果[43-47]，而并没有针对心墙坝工程的研究成果。为此，本研究参考天然土层的相关距离取值，将各个参数随机场的水平和垂直相关距离分别设定为150 m和50 m。图4为随机参数为干密度的典型参数随机场。

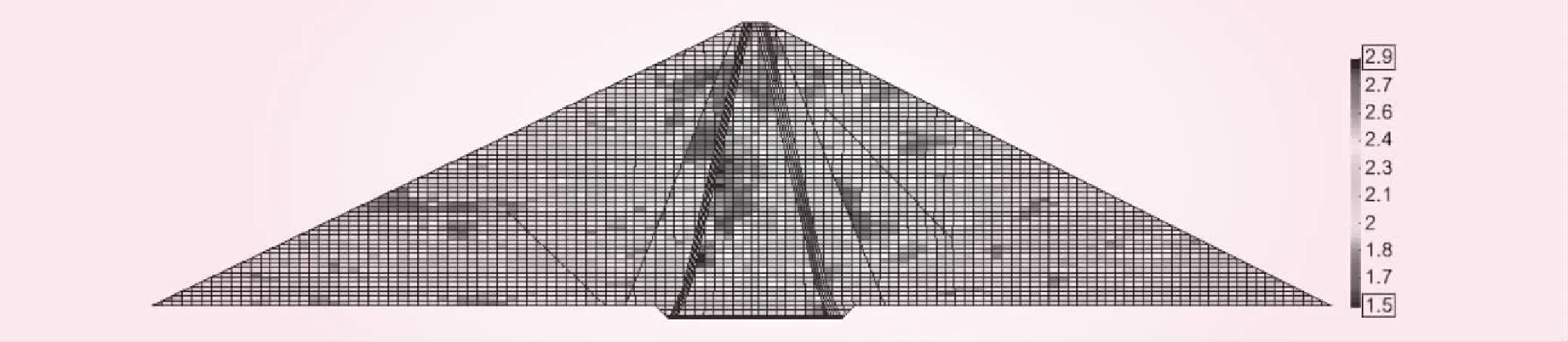
图4 不确定性筑坝堆石料参数分布示意(随机参数为干密度)

3 心墙坝地震安全性分析结果

3.1 计算结果的统计稳定性

在根据RFEM计算结果估计总体统计规律之前，先要保证计算结果达到“统计稳定”。为此，选择坝体最大震后沉降以及坝顶水平峰值加速度作为性能指标，绘出他们的滑动平均值和滑动标准差随RFEM模拟次数的变化，如图5所示，坝体最大震后沉降在模拟次数达到300时已经非常稳定，坝顶水平峰值加速度在模拟次数达到400以后也已非常稳定。因而，可以认为本文中对600次RFEM模拟结果的分析能够代表总体的统计特性。

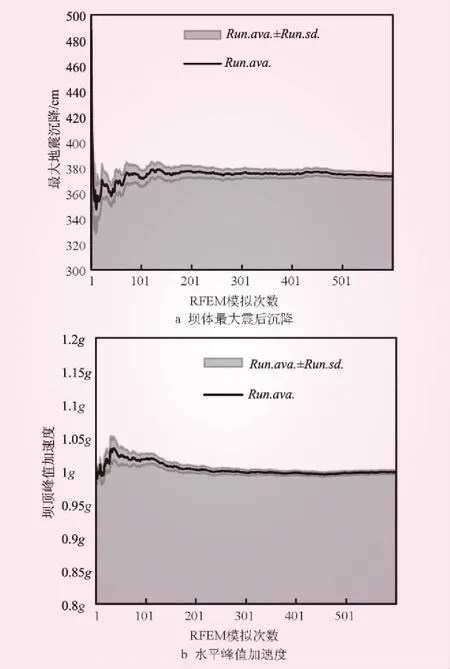
图5 随机有限元计算结果的稳定性

3.2 加速度响应

图6统计了考虑材料随机性时坝顶典型节点的水平向峰值加速度的频率分布情况，其中实线为600次RFEM计算结果的均值，虚线为不考虑材料随机性时的计算结果。表4为水平向加速度峰值计算结果的统计特征值。由表4可知，考虑材料随机性时，坝顶峰值加速度计算结果的均值(0.998 22g)略大于确定性计算结果(0.971 91g)，对应放大倍数为2.30。计算结果的离散性方面，水平向坝顶峰值加速度的极差高达约0.6g，但变异系数仅为7.44%，而90%、95%以及98%保证率对应的峰值加速度取值分别为0.109 431g、0.114 279g以及0.118 187g，分别为确定性分析结果的1.126倍、1.176倍和1.216倍。

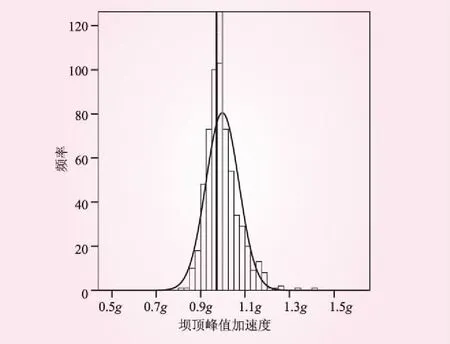
图6 坝顶水平向峰值加速度频率分布

表4 坝顶水平向峰值加速度统计参数

筑坝材料具有不确定性时，除了加速度响应的极值，加速度响应的频谱特性也具有不确定性。图7所示为坝顶典型节点加速度时程的反应谱，其中曲线为确定性有限元计算的结果，其余为4次典型RFEM的计算结果。可以看到，虽然大多数响应加速度反应谱的形状与确定性计算结果相似，但不同方案反应谱的高峰区所对应的频率范围或者峰值仍有所不同。例如，顺河向加速度方面，多数方案在0.8 Hz附近的反应谱取值已经较小，但方案3、4在0.8 Hz附近却出现了一个尖峰；方案2在1.5 Hz附近出现峰值，方案3在0.8 Hz附近出现峰值，而其他方案的峰值则都在0.2～0.3 Hz附近。类似的情况在竖向加速度反应谱图中也可观察到。加速度响应反应谱高峰区对应的频率反映了坝体的自振特性，因而上述高峰区位置不同的现象反映了筑坝材料的不确定性引起了坝体自振特性的变化。

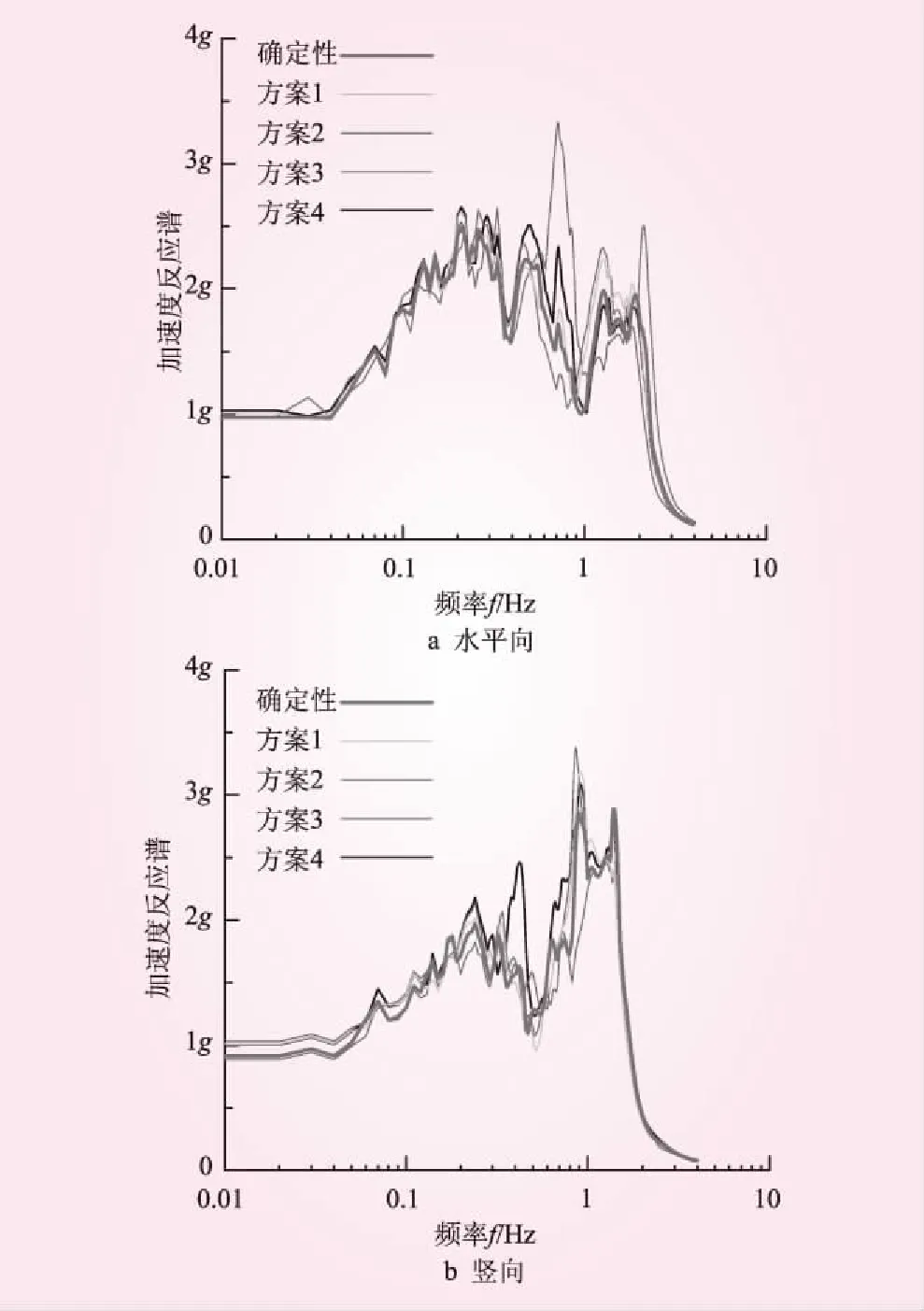
图7 坝顶加速度反应谱(典型案例)

3.3 永久变形

图8统计了考虑材料随机性时坝体最大震后沉降频率分布情况，其中实线为600次RFEM计算结果的均值，虚线为不考虑材料随机性时的计算结果，为327.3 cm。表5为最大沉降计算结果的统计特征值。由表5可知，考虑材料随机性时最大沉降计算结果的均值明显大于确定性计算结果；而确定性有限元计算结果的保证率约为25%，即在材料存在随机性的情况下，最大沉降大于确定性有限元预测值的概率约有75%。计算结果的离散性方面，最大沉降的变异系数为17.2%。若要设计值的保证率达到90%、95%和98%，最大沉降的取值分别为455.2、490.7、527.7 cm，分别为确定性分析结果的1.39倍、1.50倍和1.61倍。

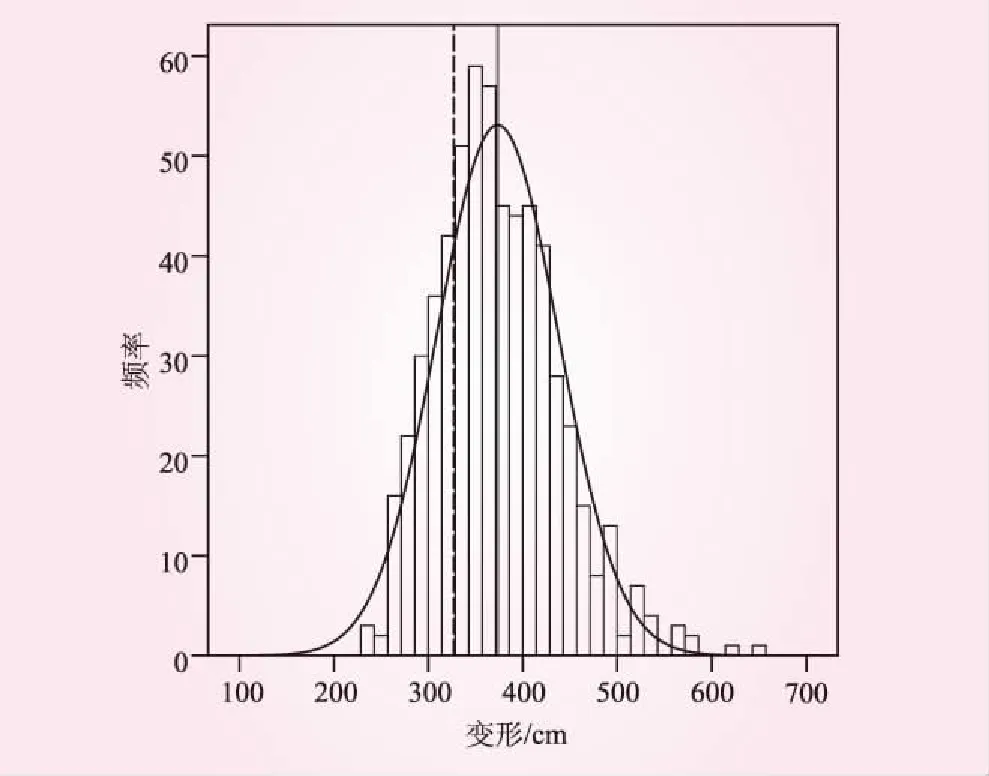
图8 震后坝体最大沉降频率分布

表5 震后坝体最大沉降统计特性

对RFEM计算得到的最大震后永久变形进行Kolmogorov-Smirnov检验以确定其是否满足正态分布，经检验，顺河向和竖直向最大永久变形的双侧渐近显著性都小于0.05%。因此，可以认为随机最大永久变形不满足正态分布。绘制最大永久变形与对数正态分布的P-P图以检验其是否满足对数正态分布，如图9所示，计算点与45°直线重合极好，由此可知随机最大永久变形满足对数正态分布。

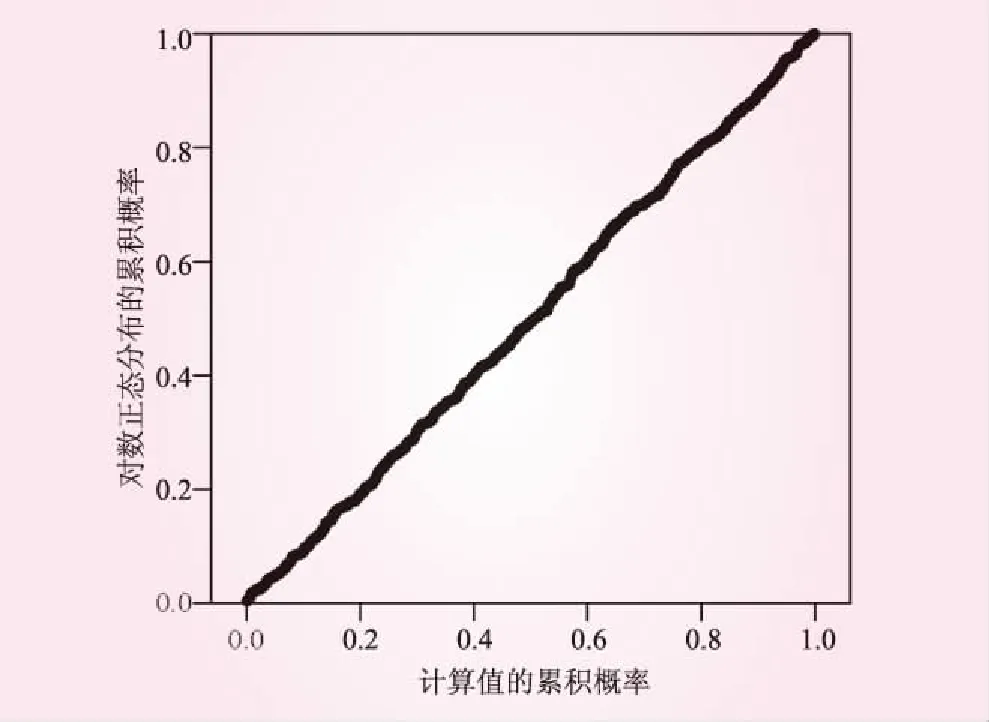
图9 震后坝体最大沉降P-P示意

4 材料物理参数随机性的敏感性分析

对材料物理参数(干密度、孔隙率、不均匀系数及平均粒径)的不确定性做敏感性分析，为堆石料填筑质量控制标准的设定提供一定参考。为此进行4组蒙特卡罗随机有限元模拟，每组分别考虑一种物理参数的随机性，各参数的变异系数取值见表3。此外，用敏感率R表征地震响应对各个物理参数随机性的敏感性，即

(4)

敏感率R的取值越大，表明坝体响应对该材料参数的敏感性越高；反之亦然。

表6为考虑各材料参数随机性时最大竖向永久变形的频率分布情况。孔隙率和干密度本身的变异系数为5%，由表6可知，孔隙率和干密度引起最大沉降的变异系数分别为6.56%和2.89%，为其本身变异系数的1.3倍和0.577；因而，在目前大坝填筑中严格控制孔隙率和干密度是非常合理的。相比之下，不均匀系数和平均粒径的变异系数为40%时引起的最大竖向永久变形的变异系数分别为11.07%和6.78%；因此，现行土石坝填筑规范并不要求对这两项参数进行非常严格控制也是合理的。但是不均匀系数和平均粒径的随机性过大也还是会对结构响应造成影响，由表6可知，考虑不均匀系数随机性时结构响应的变异系数最大，其次是考虑平均粒径随机性时，随后才是考虑孔隙率随机性时。因此，不能完全不对不均匀系数和平均粒径的随机性进行控制。

表6 考虑各个材料性质不确定性的计算结果统计(永久变形)

表7为考虑各材料参数随机性时坝顶水平峰值加速度响应的分布情况。由表6、7可知，坝顶水平峰值加速度对应各个材料参数的敏感率R普遍略低于最大竖向永久变形对应的各R值，即坝顶水平峰值加速度对材料参数随机性的敏感度略低。此外，与最大永久变形类似，峰值加速度响应对孔隙率的敏感性相对较高，其次是干密度，而对不均匀系数和平均粒径的敏感性相对较低。但是，并不代表就不需要对筑坝材料的不均匀系数和平均粒径进行控制——考虑不均匀系数的随机性时响应的变异系数仍然最大，而考虑平均粒径随机性时对应的变异系数也大于考虑干密度随机性时。

表7 考虑各个材料性质不确定性的计算结果统计(水平峰值加速度)

5 结 论

本文以某高心墙堆石坝为例，采用基于局部平均细分法的随机有限元法模拟考虑筑坝堆石料空间变异性时心墙坝的地震响应以及永久变形，据此探讨了堆石料的空间变异性对心墙坝地震安全性的影响，以及心墙坝地震响应对各随机物理参数的敏感性。主要结论为

(1)考虑筑坝材料空间变异性时，大坝峰值加速度响应的取值和频谱特性都发生一定程度的离散，为使设计方案的保证率达到90%以上，需将确定性分析得到的峰值加速度放大1.1倍～1.2倍。

(2)大坝震后最大沉降的离散程度相比更大，且为使设计方案的保证率达到90%，需将确定性分析结果放大1.4倍～1.6倍。

(3)心墙坝地震响应对堆石料孔隙率和干密度随机性的敏感性相对较高，对不均匀系数和平均粒径的随机性的敏感性较低。但是，不均匀系数和平均粒径的随机性仍然会对大坝的地震反应带来变异性，因此有必要对其随机性进行控制。

综上所述，忽略材料的不确定性可能导致低估大坝的地震反应。目前大坝填筑中严格控制孔隙率和干密度是非常合理的，而施工过程中也宜加强对堆石料级配的控制，避免其出现过大的随机性。