不同时间尺度径流的多重分形特征解析

刘树锋，关 帅，陈记臣

(1.广东省水利水电科学研究院，广东 广州 510635；2.河口水利技术国家地方联合工程实验室，广东 广州 510635；3.广东省水动力学应用研究重点实验室，广东 广州 510635)

0 引 言

由于受到人类活动、气候、地质地貌等因素的影响，径流时间序列变化过程呈现出复杂的非线性特征，探索径流的非线性特征成为水文学领域的研究热点。关于径流时间序列非线性特征的研究，较早从混沌和分形角度进行。如：1987年Hense等[1]最早在水文领域中引入了混沌分析方法；Sivakumar等[2]于2001年分析了瑞典南部Gta河流域131年(1807年1月～1937年12月)的月降雨量和月径流量序列存在混沌现象；Xu等[3]于2008年以阿拉尔水文站1958年～2005年的时间序列资料为基础，运用分形理论，揭示了塔里木河干流年径流过程的分形特征。为了能反映径流时间序列的真实特性，需考虑它们的多层次结构，而传统的方法难以分析径流时间序列非线性的多层次结构。因此，相关学者结合多重分形理论，来描述径流时间序列的多层次结构。近年来，多重分形理论作为分形几何领域的一个主要发展方向，在物理学、经济学、网络交通、通讯和图象处理、水文学等许多学科和领域有着重要的应用[4-7]。如：Labat等[8]基于岩溶流域的高度非线性和非平稳系统，分析了皮雷内埃斯山脉(法国阿里日)的3个法国岩溶泉(Aliou、Baget和Fontestorbes)上测得的降雨和径流的多重分形分析特征；Kantelhardt等[9]讨论了大时间尺度上降水和河流流量的多重分形特性；Wang等[10]以洪水时间序列为研究对象，解析武江流域洪峰流量、洪水总量、最大24 h洪量、最大48 h洪量和最大72 h洪量的多重分形特征；袁晓辉等[11]采用多重分形消除趋势波动分析法，分析了长江流域某水文站的月径流序列；张姝琪等[12]运用非参数检验法分析了咸阳站等7个站点年径流序列非平稳性波动特征。流量作为径流常用的表示方法，本文以锦江流域为对象，分析年尺度和月尺度的流量时间序列的多重分形这一内在典型特征。通过对流量时间序列内在微观分形特征进行分析，揭示其演变规律，为径流的预测、利用和管理提供合理判据和科学依据。

1 研究区域简介

锦江是珠江水系北江里浈江的西源，发源于湖南省万时山。流向自北而南，纵贯全县，在细瑶山出仁化县境，至韶关市曲江区白芒坝汇入浈江，锦江流域水系图见图1。干流长度为108 km，集雨面积为1 913 km2，主流平均比降0.171%，多年平均流量44.55 m3/s。锦江流域属中亚热带气候[13]，受季风和地形的影响较大，多年平均降雨量为1 611.0 mm，年最大降雨量2 060 mm(发生在1959年)，年最小降雨量1 117.4 mm(发生在1967年)，年平均降雨天数153 d，多年平均水面蒸发量为1 340 mm，多年平均陆地蒸发量为704.8 mm。本研究选取锦江流域作为研究对象，分析该流域1967年～2018年共52年的年、月平均流量分形特征。

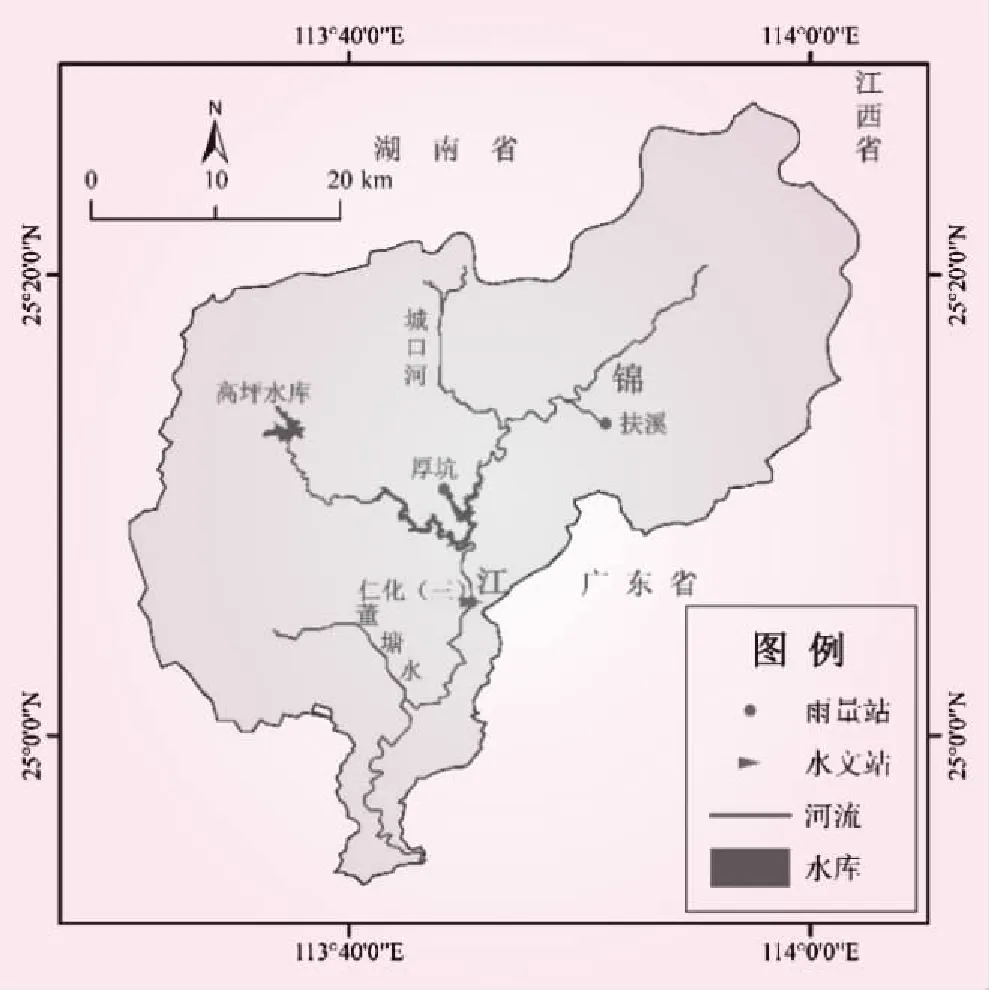
图1 锦江流域示意

2 研究方法

多重分形，又叫多标度分形，由Mandelbrot[14]在研究湍流时首次提出。多重分形通过一个谱函数来描述分形结构上不同的局域条件、或在演化过程中不同层次所导致的概率在整个集合上的分布状况，是从系统的局部出发来研究其整体的特征，并借助统计物理学的方法来讨论特征参量的概率测度的分布规律[15]。

幂谱是研究分形的重要工具，根据幂谱与频率之间的关系式

E(ω)∝ω-β

(1)

若时间序列的幂谱与幂率logE(ω)与log(ω)之间成正比关系，则表明该时间序列具有无标度性。把满足幂率的频率区间及相应的时间区间称位无标度区间，在无标度区间内，研究的对象具有无标度性，即存在自相似性，表明局部与整体在形状、性质或功能等方面是相似的。

从信息论角度，当r→0时，得到

Iq(r)=Cr-(1-q)Dq

(2)

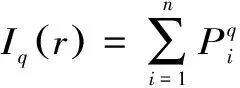
通过Legender变换得到

(3)

当时间序列的过程是多重分形过程时，则配分函数M(λ，q)随着时间标度λ的变化服从如下的幂律关系

M(λ，q)∝λτ(q)

(4)

式中，τ(q)为尺度函数(又称为“质量指数”)，可通过对双对数函数图lnM(λ，q)～lnλ中的点进行最小二乘法拟合得到，且尺度函数τ(q)有如下性质：①τ(q)是一个凹函数；②当q=0时，所有尺度函数具有相同的截距τ(0)=-1；③τ(q)是q的非线性函数。

根据τ(q)计算出奇异标度指数α和多重分形谱函数f(α)

(5)

对于存在多重分形结构的时间序列，奇异标度指数α(q)则是q的非线性的、递减的函数。其中，Δα=αmax-αmin在统计意义上反映了序列变化的程度和范围，Δα越大，说明时间序列分布越不均匀，波动幅度较大；若Δα=0，属于完全均匀的分布状况。而Δf(α)=f(α)左-f(α)右，当|Δf(α)|越大，表明该时间序列分布越不均匀，波动行为就越混乱。若Δf(α)>0，奇异谱曲线为左钩型；若Δf(α)<0，则奇异谱曲线为右钩型。

3 结果与分析

根据幂谱与频率之间的关系式，本文首先解析锦江流域年、月平均流量的logE(ω)与log(ω)之间是否为正比关系；再进一步分析锦江流域年、月平均流量在其无标度范围内的多重分形性，分析结果如图2所示。

图2 年平均流量的幂谱与频率关系曲线

图2表明锦江流域的年平均流量的幂谱与频率之间的曲线成正比关系，且logE(ω)与log(ω)的正比系数的绝对值为：1.933 9，即年平均流量的β值，说明锦江流域年平均流量具有无标度性。相似地，得出锦江流域各月流量的β值(见表1)。

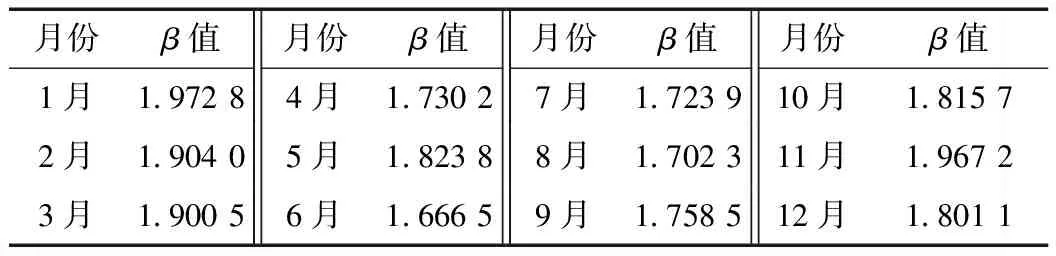
表1 各月流量的幂谱与频率关系式中的 β值

表1说明，锦江流域各月流量时间序列的β值均大于1.670 0。这表明锦江流域各月流量过程的时间序列具有无标度性。

本文进一步分析锦江流域年平均流量和月平均流量的配分函数，据此可判断锦江流域年平均流量是否具有多重分形的特性，锦江流域年、月平均流量的配分函数图见图3和图4。

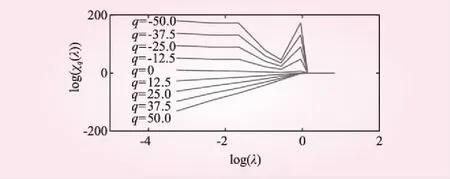
图3 年平均流量的log(λ)～log(xq(λ))关系曲线

图3和图4为q取不同值时log(λ)～log(xq(λ))的曲线簇，说明：当log(λ)<-0.55时，若q<0，log(λ)～log(xq(λ))具有良好的线性关系，q>0存在微小的波动，但整体上依旧以线性关系为主。而且随着q的增加，线与线之间的距越来越窄，直线斜率明显增大，表明锦江流域年平均流量和月平均流量具有多重分形特征。综上所述，锦江流域的年、月时间尺度的流量过程时间序列在相应的标度范围内，具有多重分形的特征。

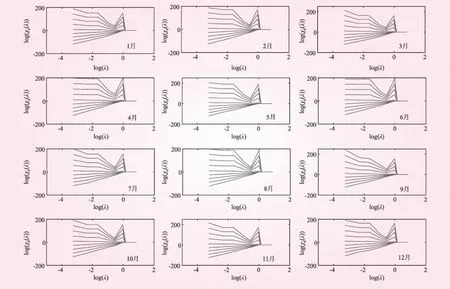
图4 各月平均流量的log(λ)～log(xq(λ))关系曲线

对锦江流域年、月平均流量进行多重分形分析，得到q～τ(q)曲线(见图5)。

图5表明锦江流域流量过程的q～τ(q)曲线为凹向q轴的曲线，q～τ(q)之间存在非线性关系，进一步说明锦江流域流量过程的时间序列具有分形结构特征；且τ(q)随着阶数q值的增加而增加，当q>0时，τ(q)随着阶数q的增加的幅度变小。

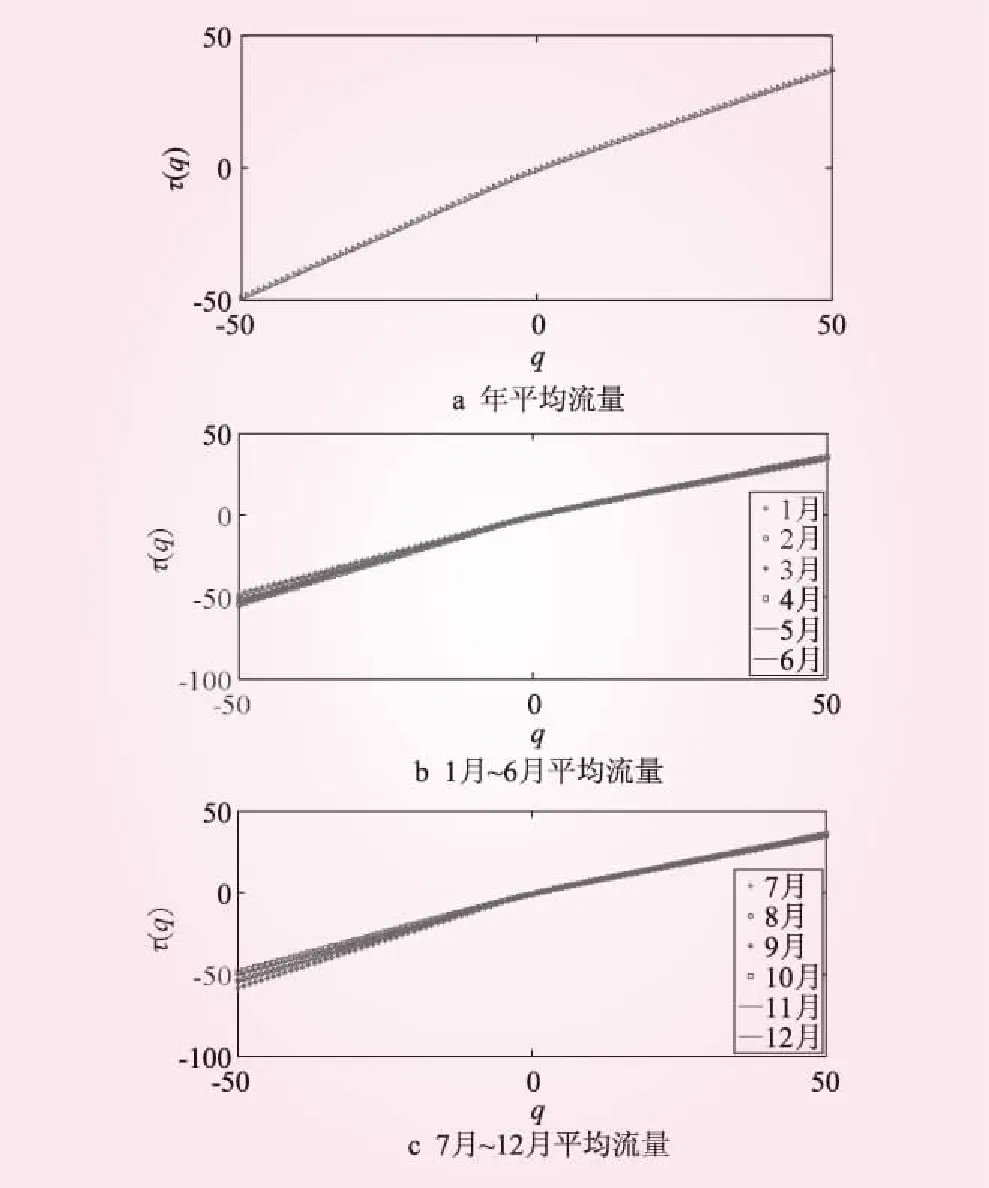
图5 锦江流域流量过程的q～τ(q)曲线

多重分形谱α～f(α)的关系图，能反映一个时间序列局部和全局的奇异性。图6和表2为锦江流域年、月平均流量的多重分析奇异谱分析结果。

图6和表2说明，锦江流域年、月平均流量的α～f(α)曲线形状均呈现左钩型和右钩型；且Δα越大，代表锦江流域流量过程分布越不均匀，波动幅度越大。具体地：年平均流量序列的多重分形谱开口Δα=0.24为最小，说明年平均流量序列的波动幅度较小；而9月平均流量序列的多重分形谱开口Δα=0.45为最大，说明9月平均流量序列的波动幅度较大，表现出强烈的多重分形特征。同样地，依据|Δf(α)|值，得到锦江流域年、月平均流量波动行为混乱程度和奇异性由小到大的排序为：10月流量<6月流量<年平均流量<12月流量<7月流量<5月流量<2月流量<1月流量<4月流量<3月流量<8月流量<9月流量<11月流量。

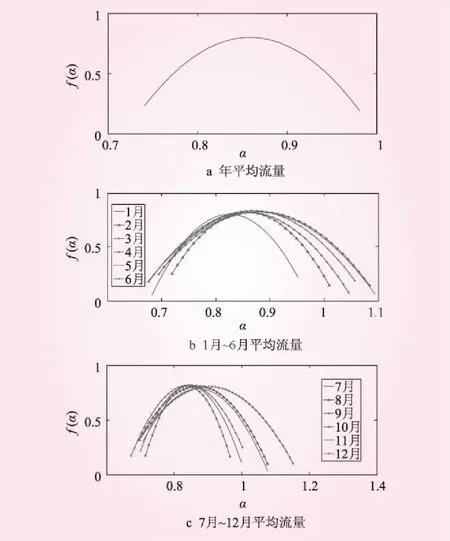
图6 锦江流域流量过程的多重分形谱

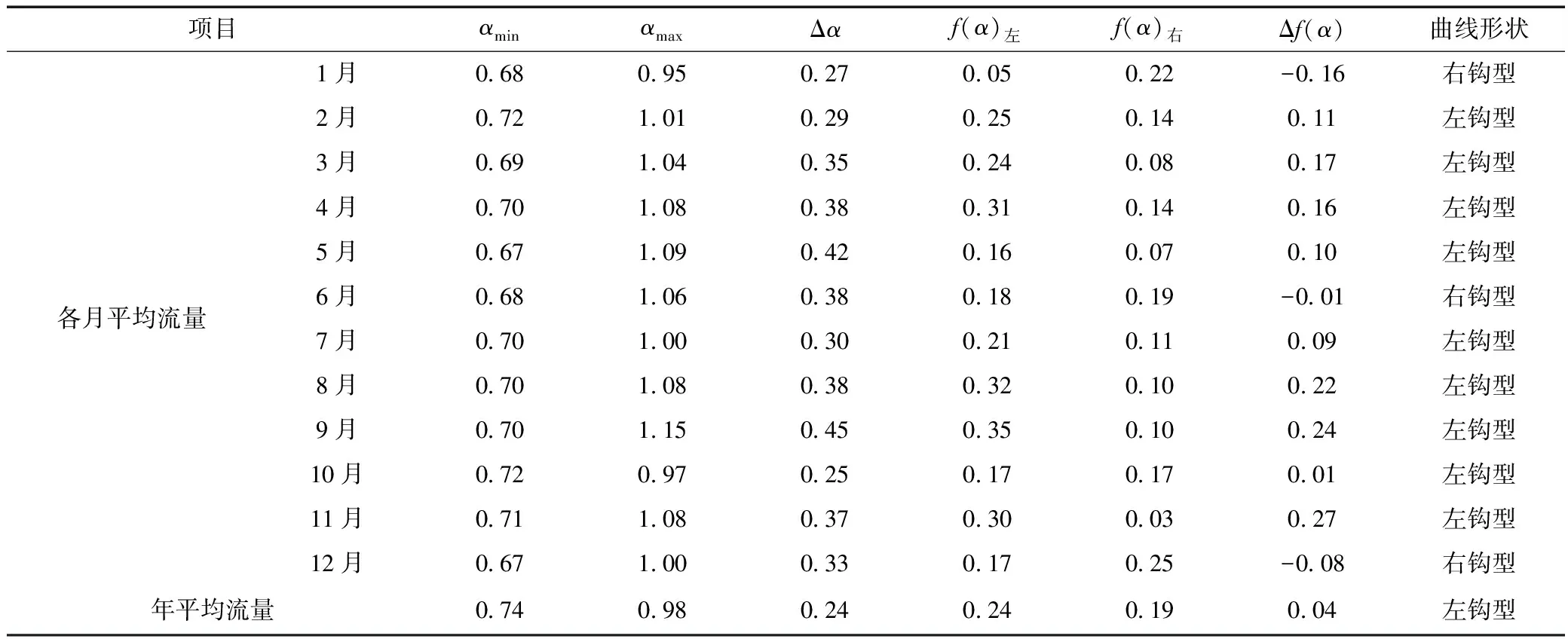
表2 锦江流域流量过程的多重分形谱函数的相关参数

4 结 论

本文通过多重分形方法，分析了锦江流域径流时间序列的非线性特征，所取得的主要成果如下：

(1)过去52年的年时间尺度和月时间尺度的平均流量，均表现出明显的多重分形特征。

(2)锦江流域12个月的月平均流量和年平均流量序列相比，年平均流量的波动幅度最小，9月平均流量序列的波动幅度较大，即9月平均流量表现出强烈的多重分形特征。

(3)锦江流域年、月平均流量波动行为混乱程度和奇异性由小到大的排序为：10月流量<6月流量<年平均流量<12月流量<7月流量<5月流量<2月流量<1月流量<4月流量<3月流量<8月流量<9月流量<11月流量。锦江流域年、月平均流量的多重分形变化特征，表明锦江流域年、月平均流量时间序列具有较为复杂的混乱特性，这为锦江流域年、月平均流量的复杂性规律的解析提供依据。