山地拖拉机坡地等高线旋耕土壤侵蚀规律研究
孙景彬 刘 琪 雒鹏鑫 杨福增 刘志杰 王 峥
(1.西北农林科技大学机械与电子工程学院, 陕西杨凌 712100;2.农业农村部北方农业装备科学观测实验站, 陕西杨凌 712100;3.西北农林科技大学林学院, 陕西杨凌 712100)
0 引言
土壤侵蚀是世界范围内土地退化的一个重要过程,严重威胁着农业的可持续发展[1]。耕作侵蚀是土壤侵蚀的重要类型之一,具体是指土壤在耕作机具的作用下发生分散、搬运和沉积的过程[2]。坡地工况的耕作侵蚀现象更为明显,会导致坡高侧的土壤耕作层变浅,坡低侧土壤严重堆积,改变了原始坡地形貌,影响后续机械化仿形作业(如播种),而且会降低土壤肥力,影响作物产量。黄土高原丘陵山区是重要农业生产区,属于国家战略“黄河流域生态保护和高质量发展”的中心区域,非常适合种植小麦、玉米等农作物,但是该地区以坡耕地、小块地居多,土壤质地疏松、抗蚀能力较差[3]。旋耕作业是该地区农业生产最基本、最重要的耕作方式之一,耕作侵蚀现象也随之产生,会威胁到坡地土壤质量以及水土流失防治工作[4]。
耕作侵蚀研究方面,研究针对的区域和作业工况分别为黄土区的牛拉铧式犁横坡耕作[5-7]、东北黑土区典型坡面的铧式犁耕[8]、川北山区的顺坡耕作[9]及紫色丘陵区的顺坡机耕[10-11]等。但针对黄土高原地区特定土壤类型,坡地等高旋耕这一常见作业工况下土壤耕作侵蚀机理研究尚未见报道。因此,有必要深入开展黄土高原丘陵山区旋耕机坡地等高旋耕侵蚀规律研究。
本文拟构建H245标准型常用旋耕刀在坡地工况下的扰土体积参数方程,分析旋耕刀坡地扰土过程的力学条件,确定坡地土壤旋耕侵蚀的主要影响因素;基于离散元仿真试验和土槽试验来探究坡地土壤在旋耕刀扰动下的迁移规律;基于多元回归分析方法探究作业参数对土壤侧向、水平位移的影响规律,并寻优确定最佳作业参数组合,为现有旋耕机在黄土高原坡耕区低侵蚀作业提供技术指导以及后续坡地专用旋耕机设计提供研究思路。
1 坡地旋耕单刀扰土与受力分析
通过构建单刀扰土体积方程、分析其坡地扰土时的受力,初步确定影响坡地旋耕侵蚀的关键因素,为仿真、土槽、实地试验研究提供理论参考。
1.1 旋耕刀坡地扰土量分析
在坡地旋耕过程中,旋耕刀对土壤的扰动量决定了耕作侵蚀的程度。首先,分析单把旋耕刀单个回转周期内切土的体积[12]。建立图1所示的直角坐标系,其中x轴为作业机具前进方向,y轴为耕深的反方向(垂直于坡面方向)。旋耕刀自身回转运动与前进运动的轨迹合成为余摆线。
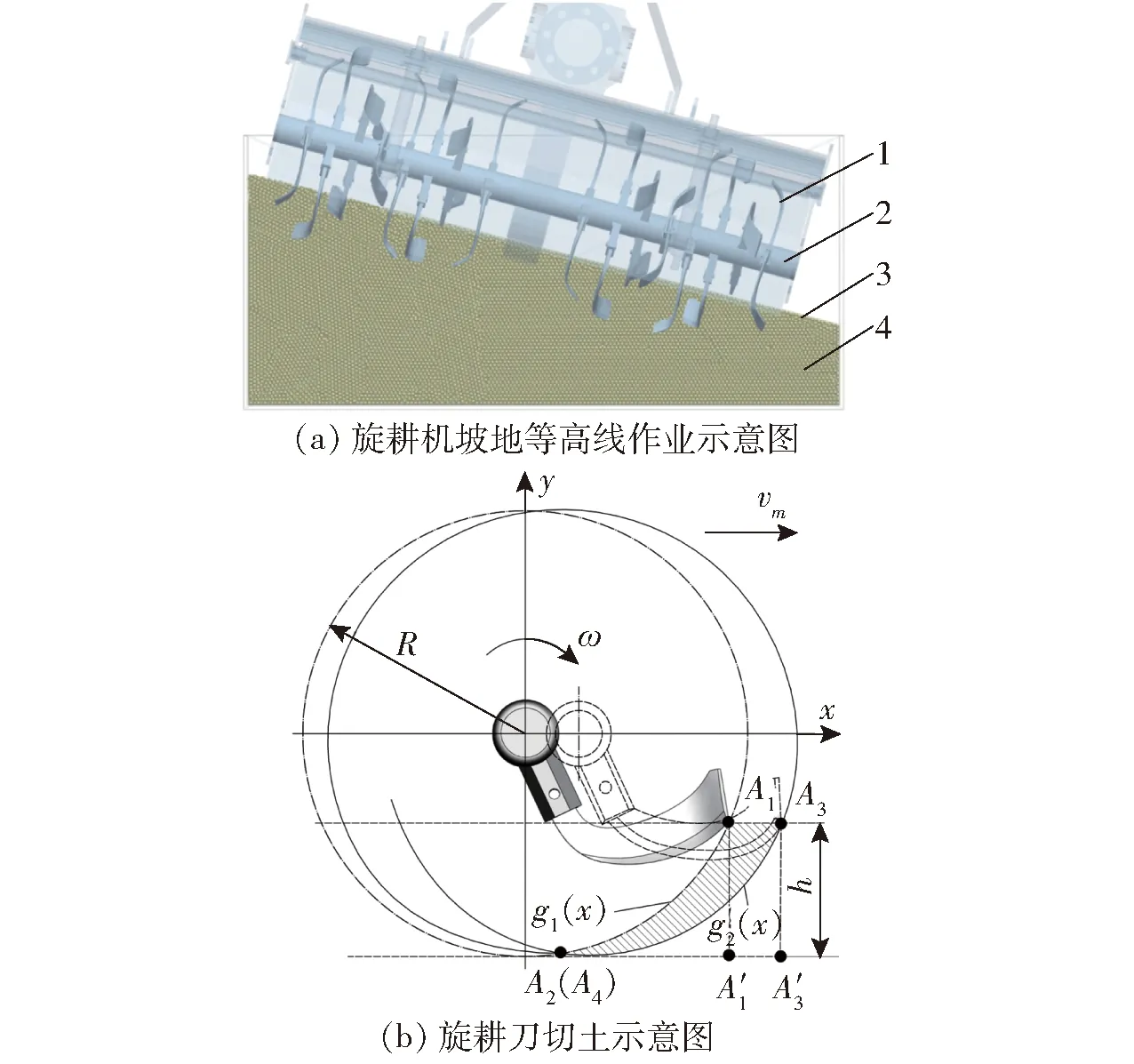
图1 旋耕刀坡地扰土分析Fig.1 Analysis of soil disturbance by rotary tillage blade on sloping land1.旋耕刀 2.旋耕刀轴 3.坡面 4.坡地土壤
图1中,A1为旋耕刀在一个回转周期内的第1次触土点,A2为旋耕刀在两个回转周期中运动的交点(第1次交点),A3为旋耕刀在一个回转周期内的第2次触土点,A4为旋耕刀在两个回转周期中运动的交点(第2次交点),A′1为过点A1垂线与坡面沟底线的交点,A′3为过点A3垂线与坡面沟底线的交点。
由图1可知,在旋耕刀的回转周期内,切土面积S方程为

(1)
式中SA1A2A′1——曲边三角形A1A2A′1面积
SA1A′1A′3A3——四边形A1A′1A′3A3面积
SA3A4A′3——曲边三角形A3A4A′3面积
g1(x)——A1A2两点间的曲线方程
g2(x)——A3A4两点间的曲线方程
x′1、x′2、x′3、x′4——点A1、A2、A3、A4沿x轴的坐标,mm
h——耕作深度,mm
R——旋耕刀回转半径,mm
旋耕刀端点的轨迹方程为
(2)
式中vm——作业机组前进速度,km/h
ω——旋耕刀轴回转角速度,rad/s
t——时间,s
联立式(1)、(2)可得

(3)
其中
(4)
式中t1、t2、t3、t4——旋耕刀过点A1、A2、A3、A4的时间
单把旋耕刀在回转周期内的切土厚度可根据面积割补法求得,将切土垡的横截面积假设为平行四边形[12]。横截面积随着旋耕刀触土深度的增大而减小。图2中旋耕刀的正切刃长度L、正切刃弯折角θ均为定值,可得切土厚度T为
T=Lsin(π-θ)
(5)

图2 旋耕刀切土厚度示意图Fig.2 Schematic of cutting soil thickness by rotary tillage blade
根据单刀的切土面积、切土厚度、z把旋耕刀切土节距s关系式(s=2πvm/(zω)),可得扰土体积为
(6)
由式(6)可知,扰土体积V主要与z、h、s、R、ω、L、θ有关,北方旱区旋耕刀轴一般采用双头螺旋结构排列,z取2。本文选用的是H245型常用旋耕刀,R、L、θ均为定值,故切土体积主要受耕作深度h、切土节距s、刀轴回转角速度ω等因素的影响。并且在刀轴回转角速度一定的情况下,切土节距直接反映的是耕作速度。因此,坡地角一定的情况下,耕作深度、旋耕作业速度及旋耕刀轴转速是影响坡地旋耕侵蚀的主要因素。
1.2 旋耕刀坡地扰土受力分析
首先,做以下假设:①土壤颗粒在旋耕刀上无相对位移。②土壤颗粒之间无相对作用力。
旋耕刀扰土过程的受力不仅与刀的结构参数、土壤参数有关,而且与坡地角密切相关,假定坡地角为α。等高线旋耕时旋耕刀轴的中心线x1应始终与坡地保持平行。以土壤颗粒作为单元体进行受力分析,可得其与旋耕刀正切面脱离的瞬间受到法向力Fa、摩擦力f、重力G及离心力Fc综合作用(图3)。

图3 旋耕刀作用下土壤颗粒空间受力分析Fig.3 Mechanical analysis of soil particles affected by rotary tillage blade
以刀柄中心面与刀轴中心线上的交点为原点O1,刀轴中心线方向(平行于坡面方向)为x1、作业机具前进方向为y1,垂直于坡面的方向为z1,建立空间直角坐标系,然后将该坐标系平移到土壤颗粒的质心O2处,得到新的空间坐标系。设土壤颗粒脱离旋耕刀正切面后的运动方向为Az。将上述土壤颗粒所受到的力分解到x2O2z2坐标系,如图3b所示,求得土壤颗粒沿着x2方向合力为
(7)
式中γ——土壤颗粒脱离时刀轴的转角,(°)
δ——x2O2y2平面与旋耕刀正切刃夹角,(°)
β——Az在x2O2y2平面投影与y2轴夹角,(°)

图4 旋耕单刀离散元仿真模型Fig.4 Rotary tillage single-knife discrete element simulation model1.旋耕刀 2.后处理选定的土壤颗粒 3.土槽模型
将离心力Fc、重力G、摩擦力f表达式代入式(7)可得
Fx=(mω2rcosγ+mgcosα)tanδ+mgsinα-
μ(mω2rcosγ+mgcosα)sinβ
(8)
式中m——土壤颗粒质量,kg
r——土壤颗粒运动回转半径,mm
μ——土壤与旋耕刀正切面间的摩擦因数
g——重力加速度,m/s2
因δ=θ-π/2,故式(8)变换为
Fx=-(mω2rcosγ+mgcosα)cotθ+mgsinα-
μ(mω2rcosγ+mgcosα)sinβ
(9)
式(9)中,可根据关系式δ=θ-π/2求得x2O2y2平面与旋耕刀正切刃夹角δ;土壤颗粒脱离时,刀轴转角γ取值范围[12]为0°~90°;土壤与旋耕刀正切面间的摩擦因数μ可通过测量得到。土壤颗粒一般会沿着x0正方向运动,力学条件为Fx>0。表明夹角β(代表了土壤颗粒运动方向)与旋耕刀的回转角速度、正切刃折弯角、坡地角有关。
综上,可得耕作深度、旋耕刀正切刃的形状、坡地角、旋耕作业速度及旋耕刀轴转速是影响坡地旋耕侵蚀的主要因素。
2 离散元仿真试验
2.1 基本假设
为了保证仿真有效性,对仿真做出假设[13-17]:①旋耕土槽仿真模型中土壤简化为球状颗粒。②考虑旋耕刀扰动后土壤颗粒粘结力对运动的影响,选用Hertz-Mindlin with JKR接触模型[18]。③旋耕过程中旋耕刀的回转速度、作业前进速度及耕深参数根据实地试验的情况进行设定。
2.2 离散元仿真模型构建
通过EDEM求解器模块对仿真时间步长、仿真时间及网格尺寸进行设置,为保证仿真的连续性,设置其仿真时间步长为1.50×10-4s,仿真时间为5 s,网格单元尺寸设置为颗粒平均半径的3倍。土槽长×宽为1.5 m×1.4 m,坡地角设置为5°、10°和15°。
基于图4a所示的HandySCAN3D型扫描仪,对H245旋耕刀进行三维结构扫描,经VXelements软件处理得到旋耕刀的STL点云模型,将STL文件导入逆向建模软件Geomagic Design X 64得到旋耕刀三维模型(图4b)。最后,将该旋耕刀的三维模型导入仿真土槽模型中,如图4c所示。将SolidWorks中建立的旋耕机整机三维模型导入仿真土槽模型中,如图5a所示,仿真作业过程如图5b所示。
基于Analyst模块进行后处理分析。在旋耕机幅宽范围的偏中间位置,垂直于坡面方向设置3个不同深度的土壤层,分别为浅层(0~50 mm,颗粒设置为蓝色)、中层(50~100 mm,颗粒设置为红色)和深层(100~150 mm,颗粒设置为绿色),如图5a所示。基于“Export Results Data”导出仿真前、后所有标记的土壤颗粒在侧向和水平方向上坐标的均值,对均值作差得到土壤颗粒沿侧向和水平方向所发生的位移。

图5 旋耕机坡地仿真试验Fig.5 Simulation test of rotary tillage on slope
2.3 旋耕单刀对土壤颗粒的扰动
为了分析单个旋耕刀扰动下土壤运动情况[19-20],对单个旋耕刀侧切刃正下方选取一定宽度和深度的土壤,共设置6个不同位置的土壤条带,设置旋耕刀的回转速度为150 r/min,旋耕前进速度为1.5 km/h,旋耕深度15 cm。图6为位于侧切刃正下方的土壤颗粒在旋耕刀回转360°扰动下沿着水平、侧向以及垂直方向的运动过程。

图6 侧切刃正下方土壤的运动情况Fig.6 Movement of soil particles under lengthwise edge
由图6可知,旋耕刀没有接触到表层土壤时,所有的土壤颗粒处于静止状态;随着旋耕刀入土,旋耕刀侧切刃与土壤颗粒的接触类型由点接触逐渐变为面接触,接触面积不断增大,旋耕刀侧切刃周围的土壤颗粒在刀刃剪切和挤压作用下开始发生相对运动。并且土壤颗粒在侧切刃的动态滑切作用下有向后运动的行为。L1~L6处深层的土壤颗粒虽然处于旋转中心范围内,但其并未与旋耕刀有直接接触,故土壤几乎不受力而保持静止状态;其余土壤颗粒与旋耕刀接触时受到短暂的水平力,在水平力作用下均随旋耕刀的切土有向后运动的行为。处于较浅层的土壤颗粒受到的作用力比中层和深层土壤颗粒的作用力大,因此,浅层土壤颗粒的位移最大。L1~L6中的土壤颗粒虽然都位于侧切刃下方,但土壤颗粒起始侧向运动的方向,取决于颗粒质心的侧向位置是否偏离于侧切刃的轴线。
旋耕刀开始入土至触土最深的过程中,侧切刃接触到的土壤颗粒会在侧切刃的作用下向更深方向运动。位于较浅层的土壤颗粒会随着刀刃的下切表现出轻微的向下运动,主要原因是其位于刀刃的切土边缘,随着刀刃的进一步向下运动,土壤颗粒不会继续向后运动,而是在原始位置由于土壤扰动作用表现出微量的下陷。位于较深层的土壤颗粒因承受上层土壤颗粒的重力,其受到垂直方向的力相对较小,故较深层中只有靠近旋耕刀旋转中心的土壤颗粒表现出较大的位移。
旋耕刀触土最深至完全出土的过程中,L4~L6处表层的土壤颗粒均表现出偏正切刃朝向一侧运动,说明旋耕刀的正切刃在一定程度上决定了土壤颗粒抛撒的方向,因此在进行坡地专用旋耕刀具的设计时应该充分考虑这一点。
L1~L6中选定的所有土壤颗粒沿侧向、水平方向、垂直方向平均位移随旋耕刀回转角的变化曲线如图7所示。

图7 单刀扰动下不同位置土壤颗粒的位移Fig.7 Displacement of soil particles in different positions under single-pole disturbance
由图7可知,随着旋耕刀转过一定的角度,土壤颗粒在侧向、水平方向以及竖直方向的位置均发生变化,其中土壤颗粒的水平位移远大于侧向、竖直位移。具体地,如图7a所示,随着旋耕刀的入土切削抛撒过程,土壤颗粒侧向的位置均表现为向坡地较低侧变化的现象,并且,土壤颗粒的侧向位置变化最大的是处于旋耕刀出土瞬间所扰动的土壤颗粒,这说明旋耕刀正切刃的弯折角很大程度上决定了土壤颗粒的侧向抛撒效果;如图7b所示,土壤颗粒的水平位置随着旋耕刀的扰动而发生变化,L2~L5位置的土壤颗粒水平位移大于L1和L6,原因是L2~L5位置的土壤在旋耕刀的此次回转周期中,处于旋耕刀的旋转中心正下方,所受的扰动程度更大一些,但是实际中沿坡地等高线旋耕作业中旋耕刀对所有土壤的扰动程度相同,并且土壤颗粒沿水平方向位移与旋耕刀轴转速和机组作业前进速度密切相关;如图7c所示,随着旋耕刀的入土,大部分土壤颗粒垂直位置会呈现出先变深后变浅的趋势,主要原因是在旋耕刀的侧切刃作用下,土壤颗粒首先会出现一定程度的下陷,随后会滑出刀刃的边界被刀刃抛撒,颗粒被抛撒的程度与其相对于正切刃的位置有关,旋耕刀出土时,正切刃所扰动位置的土壤颗粒在垂直方向上的位移最大。
2.4 旋耕机对土壤颗粒的扰动
为了深入探究旋耕机整机作业参数(旋耕刀轴转速、作业前进速度)及坡地角对土壤颗粒在侧向和水平方向的位移规律,参照文献[21-22]的方法,采用控制变量法进行了单因素仿真试验。
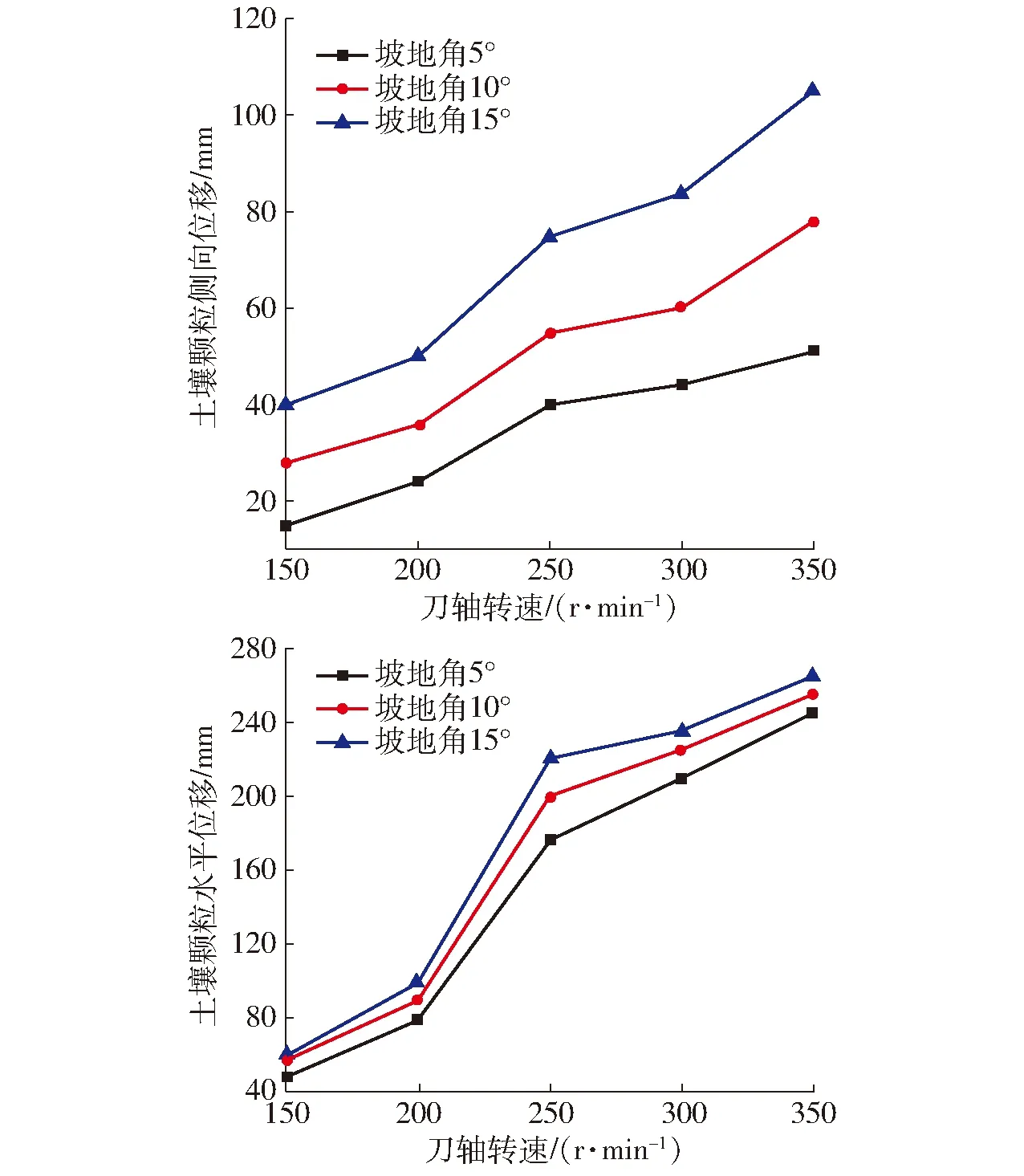
图8 不同旋耕刀轴转速下土壤颗粒位移变化曲线Fig.8 Soil particle displacement change curves at different rotation speeds of rotary tillage blade shaft
设置耕作深度15 cm,旋耕作业前进速度1.5 km/h,在不同坡地角、不同旋耕刀转速作用下,得到3个深度层土壤颗粒的平均侧向位移和水平位移如图8所示。
由图8可知,土壤颗粒的侧向位移以及水平位移均随着刀轴转速的增加而增加,主要原因在于旋耕刀的转速越高,对土壤颗粒的抛撒程度越大。并且坡度越大,侧向位移随刀轴转速增大的程度会越大,主要原因在于旋耕刀的转速高,其对土壤颗粒的抛撒程度大,从而使得土壤颗粒被抛起的高度大,降落过程中,在重力沿着坡面向下分力作用下运动位移变大。在转速150~250 r/min区间内,随着刀轴转速的增大,颗粒的水平位移增大程度远大于侧向位移。
设置耕作深度15 cm,旋耕刀轴转速250 r/min,在不同坡地角、不同旋耕作业前进速度下,得到3个深度层土壤颗粒的平均侧向位移和水平位移如图9所示。

图9 不同旋耕作业速度下土壤颗粒位移变化曲线Fig.9 Soil particle displacement change curves at different rotational tillage speeds
由图9可知,土壤颗粒的侧向位移以及水平位移均随着作业速度的增加而降低。作业前进速度越小,单位时间内土壤颗粒所受到旋耕刀的扰动次数越多,导致土壤的抛撒程度增大。土壤颗粒的水平位移方向与机组前进方向相反,并且水平位移较侧向位移受旋耕作业速度的影响更为显著,当旋耕作业速度由0.5 km/h增加到1.5 km/h时,土壤颗粒沿旋耕作业方向的位移增加了近50%。
3 坡地旋耕土槽试验与实地试验
3.1 试验方案
于2021年10月,分别在西北农林科技大学机械与电子工程学院土槽实验室和坡地专用试验场进行了坡地旋耕土槽试验和实地试验[23-24]。其中,土槽试验主要用于探究不同试验因素对旋耕机坡地旋耕侵蚀总体扰土量的影响规律,实地试验主要用于探究不同试验因素对不同深度、不同大小颗粒土壤的位移影响规律[25]。按照GB/T 5668—2008《旋耕机》规定的试验方法进行试验。
坡地旋耕土槽试验与实地试验的机器系统分别如图10、11所示,土槽试验系统主要包括土槽测试车、镇压器、旋耕机等;实地试验系统主要包括自主研发的姿态调整山地履带拖拉机、125型旋耕机(旋耕刀为H225型)、直尺、卷尺、土壤示踪器(3种尺寸的铝块)以及自行搭建的示踪器位置坐标测定台架,该台架主要用来测定土壤在旋耕前后沿着各个方向的位移。

图10 坡地旋耕土槽试验Fig.10 Rotary tillage experiment in soil trough1.土槽测试车 2.旋耕机 3.坡地 4.土壤收集条带

图11 坡地旋耕实地试验Fig.11 Field test of rotary tillage on sloping land1.山地履带拖拉机 2.坡地自适应悬挂系统 3.旋耕机 4.坡地 5.示踪器位置坐标测定台架 6.土壤含水率测定仪 7.土壤紧实度测定仪 8.示踪器(铝块)
3.2 土壤位移测量方法
旋耕试验前,塑造坡地角(5°、10°、15°)并压实土壤,然后在每个土壤示踪器(铝块)的表面用记号笔编写序号,将土壤示踪器按照一定的规律进行编号,按照图12所示的埋设方案,将其布设在3种不同深度的土层中(表层0~50 mm、中层50~100 mm和深层100~150 mm各埋设45个示踪器,即图12中示意的3种颜色各有45个),并采用坐标测定台架测量并记录此时每个示踪器的初始二维坐标[18]。在试验中,将小区坡地划分为3个区段,每个区段间隔为1 m,此时在拖拉机旋耕机组一次旋耕过程就进行了3次重复试验。最后,追踪所有带有编号的土壤示踪器,用坐标测定台架测量并记录其最终二维坐标,对每个示踪器的最终二维坐标与初始二维坐标取差值,即得到示踪器沿着水平和侧向两个方向的位移。所有示踪器的水平位移、侧向位移分别取均值得到最终结果。

图12 土壤示踪器埋设布置方案示意图Fig.12 Schematic of soil tracer burial layout scheme
3.3 耕作参数对旋耕机扰土迁移量的影响
坡地土壤旋耕侵蚀的扰土迁移量一般是指单位长度坡地范围内,在耕作后土壤从坡地较高侧向较低侧的输送量。坡地旋耕土槽试验(图10b)中,首先将长度为4 m的土壤收集带整齐铺放到坡地较低侧,旋耕完成后,收集输送迁移的土壤,并用电子秤称量,进而得到在不同作业参数下的旋耕侵蚀扰土迁移量。
按照控制变量法,设定土槽测试车的前进速度(即旋耕作业速度)为0.5 km/h,得到不同旋耕刀轴转速下侧向扰土量如图13a所示;设定旋耕刀轴转速350 r/min,得到不同旋耕作业速度下的侧向扰土量如图13b所示。

图13 旋耕作业参数对旋耕机扰土迁移量的影响Fig.13 Effect of rotary tillage parameters on soil displacement
由图13可知,在旋耕作业速度一定的情况下,旋耕机扰动导致的土壤迁移量随着旋耕刀轴转速的增大而增大,并且坡地角越大,土壤侧向迁移量明显增大;旋耕刀轴转速一定的情况下,随着旋耕作业速度的增大,土壤侧向迁移量明显减小。上述试验结论与仿真试验一致。
3.4 耕作参数对土壤颗粒宏观运动的影响
为了进一步验证仿真试验、土槽试验结论的准确性,以及深入分析3种深度土层中的不同粒径土壤颗粒在所设定旋耕参数下的运动规律,进行了坡地旋耕实地试验。
3.4.1刀轴转速对土壤位移的影响
设定坡地角15°,山地拖拉机作业前进速度1.5 km/h,得到刀轴转速对不同深度层上不同粒径土壤颗粒位移影响如图14所示。
由图14可知,土壤的水平位移和侧向位移均随着刀轴转速的增加呈现增大趋势。原因在于,旋耕转速越高,土壤被抛撒的程度越高,从而导致土壤的位移越大。水平位移随着刀轴转速的增加程度大于侧向位移随刀轴转速的增加程度。因此,在坡地工况下,刀轴转速的变化对土壤水平运动的影响程度大于其对土壤侧向运动的影响。土壤的水平位移总是大于侧向位移主要是因为旋耕刀在切土的过程中,其对土壤沿水平方向的抛撒作用大于沿侧向的抛撒作用。该结论与方会敏等[19]的研究结论一致。并且,土壤颗粒越小,其侧向、水平位移会越大,可以用动量定理解释这一规律。

图14 刀轴转速对不同深度层土壤位移的影响Fig.14 Effect of blade shaft rotation speed on soil displacement at different depths
3.4.2旋耕作业速度对土壤位移的影响
设定坡地角15°,旋耕刀轴转速300 r/min,得到旋耕作业速度对不同深度层的土壤位移影响如图15所示。
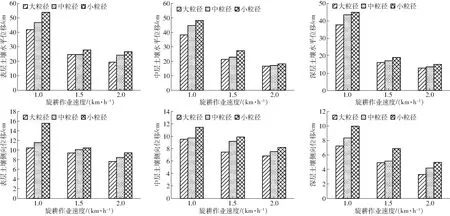
图15 旋耕作业速度对不同深度层土壤位移的影响Fig.15 Effect of forward speed of rotary tillage operation on soil displacement at different depths
由图15可知,土壤的水平位移和侧向位移均随着作业速度的增加呈现减小的趋势。原因在于,作业速度越大,在某一耕作区域土壤扰动的时间减少,导致对土壤的扰动程度减小。土壤的水平位移随着作业速度的增加而减小的程度较侧向位移大,原因在于,作业速度增大,土壤向机组行驶前进方向移动的程度增加。
3.4.3坡地角对土壤位移的影响
设定旋耕刀轴转速300 r/min,旋耕作业速度1.5 km/h,得到坡地角变化对不同深度层土壤位移影响如图16所示。

图16 坡地角对不同深度层土壤位移的影响Fig.16 Effect of slope angle on soil displacement at different depths
由图16可知,土壤的水平位移和侧向位移均随着坡地角的增加呈现增大的趋势。原因在于,坡地角越大,土壤被抛撒起来之后,土壤颗粒在重力的分力以及旋耕刀的扰动下继续向坡低侧迁移;水平位移随着坡地角增加程度远小于侧向位移随坡地角的增加程度。随着土壤颗粒所处深度的增加,其水平和侧向的位移均变小,主要是因为旋耕刀的扰动发生时,较深层次的土壤颗粒受到其周围土壤的阻碍程度越大,因此其位移会相应减少。
3.5 正交试验
3.5.1正交试验方案
为了进一步探究坡地角、旋耕刀轴转速、旋耕作业速度3因素对土壤水平位移和侧向位移2个指标的综合影响,并构建坡地旋耕作业过程中土壤沿侧向和水平位移的相关参数模型,根据Design-Expert软件中的Box-Behnken Design组合设计原理,以土壤水平位移和侧向位移作为试验指标,设计了三因素三水平正交组合试验。因素编码如表1所示。正交试验结果如表2所示,A、B、C为因素编码值。
3.5.2回归数学模型建立和显著性检验
表2中的结果经Design-Expert软件处理得到方差分析结果(表3)。
对试验数据进行二次多元回归拟合,得到土壤侧向位移、水平位移的二次多元回归方程分别为
Y1=6.06+3.43A+1.33B-1.25C+0.85AB-
1.05AC-0.6BC-0.68A2+1.07B2-0.08C2
(10)
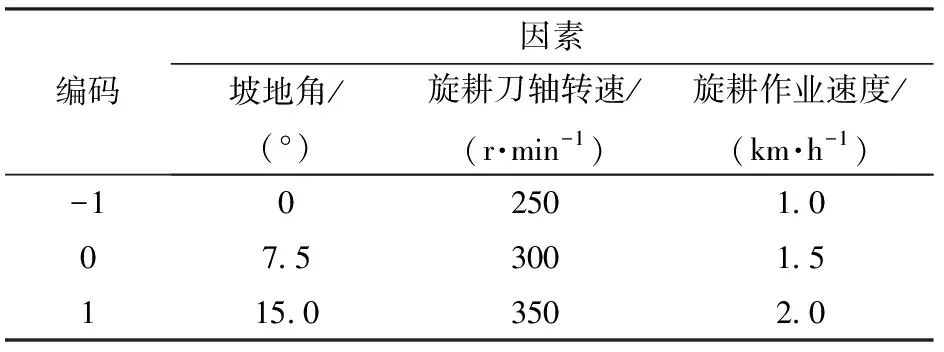
表1 试验因素编码Tab.1 Codes of factors

表2 正交试验结果Tab.2 Results of orthogonal test
Y2=20.24+1.71A+0.94B-3.85C-0.15AB-
1.73AC-0.075BC+0.08A2-2.27B2+2.31C2
(11)

表3 正交试验方差分析Tab.3 Varance analysis of orthogonal test result
A、B、C、AB、AC、A2、B2对土壤侧向位移影响均显著(P<0.05)。失拟项P值为0.113 5(P>0.05),回归方程不失拟。决定系数(0.985 0)与校正决定系数(0.965 8)均接近于1,表明回归方程拟合度很高,精密度为24.925,大于4,表明该回归方程在设计域内预测性能良好。各因素对土壤侧向位移显著性的影响由大到小依次为:坡地角、旋耕刀轴转速、旋耕作业速度。
A、B、C、AC、B2、C2对土壤水平位移影响均显著(P<0.05)。失拟项P值为0.089 6(P>0.05),回归方程不失拟。决定系数(0.980 3)与校正决定系数(0.954 9)均接近于1,表明回归方程拟合度很高,精密度为25.012,大于4,表明该回归方程在设计域内预测性能良好。各因素对土壤水平位移显著性的影响由大到小依次为:旋耕作业速度、坡地角、旋耕刀轴转速。
3.5.3各因素对性能指标影响效应分析
采用降维法对坡地角、旋耕刀轴转速、旋耕作业速度中的任一项调至零水平,得到每组显著的交互作用对土壤侧向位移和土壤水平位移的响应曲面图,如图17所示。
对于土壤侧向位移Y1,当旋耕作业速度为1.5 km/h时,坡地角与旋耕刀轴转速的交互作用响应曲面如图17a所示。当坡地角一定时,土壤侧向位移Y1随着旋耕刀轴转速的增加而增加;当旋耕刀轴转速一定时,土壤侧向位移Y1随着坡地角的增加而增加。上述两因素的交互作用中,坡地角对土壤侧向位移Y1的影响更为显著。

图17 土壤侧向、水平位移响应面Fig.17 Response surface of soil lateral and horizontal displacement
对于土壤侧向位移Y1,当旋耕刀轴转速为300 r/min时,坡地角与旋耕作业速度的交互作用响应曲面如图17b所示。当坡地角一定时,土壤侧向位移Y1随着旋耕作业速度的变化不明显;当旋耕作业速度一定时,土壤侧向位移Y1随着坡地角的增加而急剧增加。
对于土壤水平位移Y2,当旋耕刀轴转速为300 r/min时,坡地角与旋耕作业速度的交互作用响应曲面如图17c所示。当坡地角一定时,土壤水平位移Y2随着旋耕作业速度的增大明显减小;当旋耕作业速度一定时,土壤水平位移Y2随着坡地角的增加而增加。上述两因素交互作用中,坡地角对土壤水平位移Y2的影响更显著。
3.5.4参数优化
根据以上试验结果,以土壤侧向位移最小、水平位移最小为优化目标,将坡地角设定为0°~15°范围内的某一定值(如3°、6°、9°、12°、15°),对旋耕刀轴转速和旋耕作业速度进行优化求解,得到在不同坡地角下的作业参数组合,如表4所示。

表4 不同坡地角下最优作业参数组合Tab.4 Optimal working parameter combination at different slope angles
由表4可知,在坡地角0°~15°范围内设定的5个坡地角中,优化解与验证值基本一致,优化解可信。该结果可有效指导现有旋耕机在黄土高原坡地作业时的参数设定。
4 结论
(1)构建了H245标准型常用旋耕刀在坡地工况下的扰土体积参数方程,对旋耕刀进行了坡地扰土过程的力学分析,确定了导致坡地旋耕土壤侵蚀的主要影响因素为坡地角、耕作深度、旋耕刀轴转速及旋耕作业速度。
(2)基于EDEM离散元仿真软件研究了单把旋耕刀和旋耕机整机的坡地扰土规律。单把旋耕刀仿真得出:土壤颗粒在旋耕刀侧切刃的动态滑切作用下有向后运动的行为,浅层土壤颗粒位移最大,深层土壤颗粒位移最小,并且深层中靠近旋耕刀回转中心的土壤颗粒位移最大;土壤的侧向位移方向受旋耕刀正切刃朝向的影响,正切刃的弯折角很大程度决定了土壤颗粒的侧向抛撒效果;随着旋耕刀的入土,土壤颗粒的垂直位置呈现出先变深后变浅的趋势。旋耕机仿真得出:土壤颗粒的侧向、水平位移均随着刀轴转速的增加而增加,随着旋耕作业速度的增加而降低。
(3)选取刀轴转速、旋耕作业速度和坡地角作为试验因素,进行了坡地旋耕土槽试验和实地试验。坡地旋耕土槽试验得出:旋耕机扰动导致的土壤迁移量随着旋耕刀轴转速的增大而增大,随着旋耕作业速度的增大而减小。坡地旋耕实地试验得出:土壤水平、侧向位移均随着刀轴转速的增大而增大,水平位移随着刀轴转速的增加程度大于侧向位移随刀轴转速的增加程度;土壤的水平、侧向位移均随着作业速度的增大而减小,水平位移随着作业速度增大而减小的程度大于侧向位移;土壤的水平、侧向位移均随着坡地角的增大而增大,水平位移随着坡地角增加程度远小于侧向位移。并且,土壤颗粒越小,其侧向和水平位移越大。
(4)以坡地角、旋耕刀轴转速、旋耕作业速度为试验因素,土壤侧向位移和土壤水平位移作为试验指标进行正交试验,得到土壤侧向位移和水平位移与自变量之间的回归方程;方差分析得到影响土壤侧向位移的主次因素为坡地角、旋耕刀轴转速、旋耕作业速度,影响土壤水平位移的主次因素为旋耕作业速度、坡地角、旋耕刀轴转速;经参数寻优得到在5个随机设定的坡地角下旋耕机最优作业参数组合。

