基于荷载试验的钢混叠合梁技术评定研究

鞠森森　钱若霖　黄春晖　赵春晨

摘要：对于现役桥梁的管养小修、对于旧桥的评定加固已成为公路桥梁、市政桥梁建设单位一项举足轻重的工作，本文采用成桥荷载试验研究的评定方法，针对某钢混叠合梁桥梁，通过静载试验研究各主要截面的应力状况、挠度变形，通过环境激励和跑车试验研究桥梁的自振特性和冲击系数。研究表明：该桥的应力和挠度校验系数均小于1.0，表明结构工作状态处于弹性阶段，强度符合设计要求;桥梁基频、阻尼比、冲击系数等动力特性结果均满足规范要求，表明桥梁整体性较强，刚度符合设计要求。基于静动载试验结果，提出了一种置信度优化校验系数区间的方法，有效避免了因数据随机性和离散性过大引起的试验结果精度不足的问题，精确了校验系数的区间范围，给同类桥梁静载试验分析提供一定的借鉴意义。

关键词：钢混叠合梁;荷载试验;置信度;区间估计

中图分类号：U446.1

文献标识码：A文章编号：1001-5922（2022）06-0102-06

Research on technical evaluation of steel composite beams based on load test

JU Sensen， QIAN Ruolin， HUANG Chunhui， ZHAO Chunchen

（Civil Engineering College， Shannxi Polytechnic Institute， Xianyang 712000， Shaanxi China

）

Abstract：The maintenance and small repair of existing bridges and the assessment and reinforcement of old bridges have become a pivotal task for highway bridges and municipal bridge construction units. This paper adopts the evaluation method of bridge load test research， for a steel-concrete composite beam bridge， the stress conditions and deflection deformation of each main section are studied through static load tests， and the natural vibration characteristics and impact coefficients of the bridge are studied through environmental excitation and sports car tests. Research shows that the bridges stress and deflection calibration coefficients are both less than 1.0， indicating that the structural working state is in the elastic stage and the strength meets the design requirements; the fundamental frequency， damping ratio， impact coefficient and other dynamic characteristics of the bridge meet the requirements of the specification， indicating that the rigidity meets design requirements. Based on the static and dynamic load test results， a method for confidence optimization of the calibration coefficient interval is proposed， which effectively avoids the problem of insufficient accuracy of the test results caused by the excessive randomness and dispersion of the data， and precise the interval range of the calibration coefficient， providing a certain reference meaning for the static load test analysis of similar bridges.

Key words：steelconcrete composite beam; load test; confidence; interval estimation

无论是新建桥梁或是在役桥梁，定期检测和维修是提高其耐久性的重要手段。目前对于桥梁结构构件技术状况及承载能力的评价方法主要有5种[2-4]：外观调查、设计规范方法、专家经验方法、结构可靠性理论方法以及荷载试验方法。据报道，通过對5座桥的实际评估结果分析，与规范对比提出了改进建议[5];从标准种类、评定手段、评定过程、病害等级和优缺点等方面入手对多种评定方法进行分析研究并提出了优化建议[6];随机抽取国省干线公路桥梁，分别采用《公路桥涵养护规范》和《公路桥梁技术状况评定标准》对桥梁技术状况进行评定，总结了两种规定下桥梁技术状况评定的特点[7];基于桥梁部位、适应性、刚度退化及病害发展趋势等因素在评定过程中无法合理考虑的问题，优化了桥梁技术状况评定方法[8]。0F6D8556-6ACD-4637-8135-A62BF25AC6C0

因此，荷载试验作为最直接有效的一种评定桥梁技术状况和承载能力的技术方法，从定量化的角度对其进行研究，优化校验系数取值，提高评估结果可靠度，对于发现桥梁结构的隐蔽病害，确保桥梁安全性能具有重要意义。

1工程概况及有限元分析

某高速公路桥梁主桥为单孔简支钢混凝土叠合梁，对应下部结构桥墩采用群桩排架墩，基础为桩基础。桥面横坡坡度为2%（单向坡），纵坡坡度为1.1%。设计汽车荷载等级为公路-I级，设计时速为80 km/h，桥梁横断面布置：0.5 m+15.25 m（行车道）+0.5 m，试验联桥墩平均高度为25.25 m。桥面铺装采用10 cm厚沥青混凝土。

采用结构设计软件MIDAS/civil，构建主桥有限元模型，主梁由C50混凝土和Q345钢材构成，弹性模量分别取3.45×10⁴、20.6×10⁴ MPa，容重分别为25、76.98 kN/m³;桥面铺装采用二期恒载的形式施加，容重为24 kN/m³。

主梁选用梁单元形式，支座选用一般支承模拟其边界条件，静力特性分析考虑换算截面，动力特性分析采用空间迭代法，有限元离散模型和设计车道荷载作用下的跨中弯矩包络图如图1和图2所示。

2静力加载试验

根据桥梁一般检测及静力荷载试验实测数据，结合结构有限元分析计算成果，根据应变校验系数对结构强度进行分析，挠度校验系数对结构刚度进行分析，从而得到桥梁结构安全使用性能的评定结果。

在實际判断桥梁现状安全性能和承载能力时，《公路桥梁荷载试验规程》（JTG/T J21-01—2015）[9]给出量化结果，即结构校验系数指标，通过试验结果和理论结果之比，得到各主要测点校验系数，其表达式：

η=S_e/S_s

式中：S_e为在实际试验荷载下所测量的弹性变位（或应变）试验值;S_s为在试验加载作用下，某工况的控制截面内力或位移（或应变）的最大计算效应值。

当η≤1时，表明结构具备足够的承载能力，有一定的安全储备;当η>1时，则表明结构可能存在储备不足的问题，需进一步计算分析其承载能力。

2.1测试截面选择和测点布置

根据有限元分析对结构内力分析结果，确定桥梁结构的弯矩控制截面、挠度控制截面，选定跨中截面、1/4跨处截面桥梁测试截面分别为Ⅰ-Ⅰ截面、Ⅱ-Ⅱ截面，测试截面分布如图3所示。

Ⅰ-Ⅰ、Ⅱ-Ⅱ截面各布置30个正应变（应力）测点（不包括温度补偿片），全桥共布置应变测点60个;Ⅰ-Ⅰ、Ⅱ-Ⅱ截面各布置6个挠度测点，在10^#～11#桥墩的1^#、3^#、6^#T梁靠近支点处布置支点沉降测点，作为Ⅰ-Ⅰ、Ⅱ-Ⅱ截面挠度值修正依据;全桥共布置挠度测点12个，测点布置位置如图4所示。

为保证主要测试截面试验荷载加载效率在0.85～1.05[3]，经过计算分析，静载试验选用6辆汽车（均为3轴），每辆汽车车体重和荷载重共计375 kN，每个截面分别进行中载和偏载工况加载，共计6个工况;中载和偏载工况，标准加载车的横向分布位置如图5所示。

2.2静载应变结果

为保证结构构件在加载过程中处于弹性工作状态，其相对残余应变值结果需在20%以内。因此，对静载试验应变校验系数结果进行分析，同时以相对残余应变作为参照，验证数据可靠度。在荷载作用下，

每个工况对应控制截面应变实测值、理论计算值以及校验系数值如表1所示;校验系数分布如图6所示;主梁沿腹板方向应变值变化典型图，如图7所示。（其中应变结果以受拉为正;受压为负。）

根据实测值分析，不同试验工况下各底板应变相对残余值在0%～17.6%，表明主梁在试验期间，处于弹性受力阶段。由表1及图6可知，在保证加载效率0.85～1.05的实际车辆荷载作用下，每个工况底板测点应变校验系数在0.63～0.98;其中大于0.90的应变校验系数有2个，表明梁整体安全度足够，全桥应力状况符合规范和设计要求。

由图7可知，主梁各控制截面腹板测点应变基本上呈三角形线性分布，表面主梁应力受力合理可靠。

2.3静载挠度结果

对静载试验挠度校验系数结果进行分析，同时以相对残余应变作为参照，验证挠度数据可靠度。在试验荷载作用下，每个工况相应控制截面的挠度实测值、理论计算值以及校验系数值如表2所示。

现对上述24个数据进行分组，基于斯特吉斯经验公式[10]计算分组数为：

n=1+3.322lgN

=1+1.322×lg27=5.755

（取整数为6）

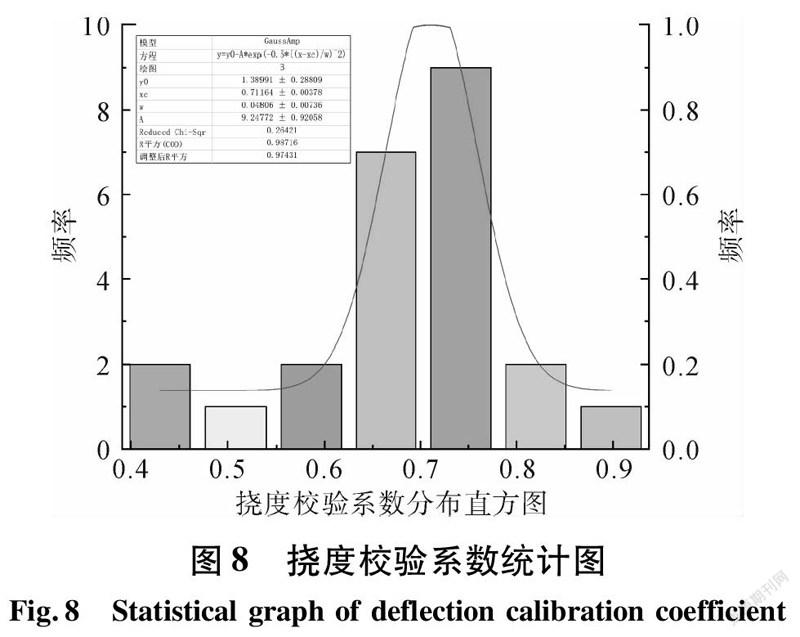
因此，根据样本最大值和最小值可计算出每组数据范围为0.078，可进一步计算出起始下限值为0.39。因此，将每组频数、频率计算结果列于表3中;并对频数分布直方图进行绘制，结果如图8所示。

由图8可知，各工况下挠度校验系数基本上服从正态分布规律，现根据95%的置信度，对各工况下的挠度校验系数进行区间估计，置信区间为[μ-2σ，μ+2σ]，即在不同的静载工况下，该钢混凝土叠合梁桥的挠度校验系数取值范围为0.62～0.81，结构刚度具有足够的安全富余度，满足规范和行车要求。

3动力特性试验

3.1自振特性

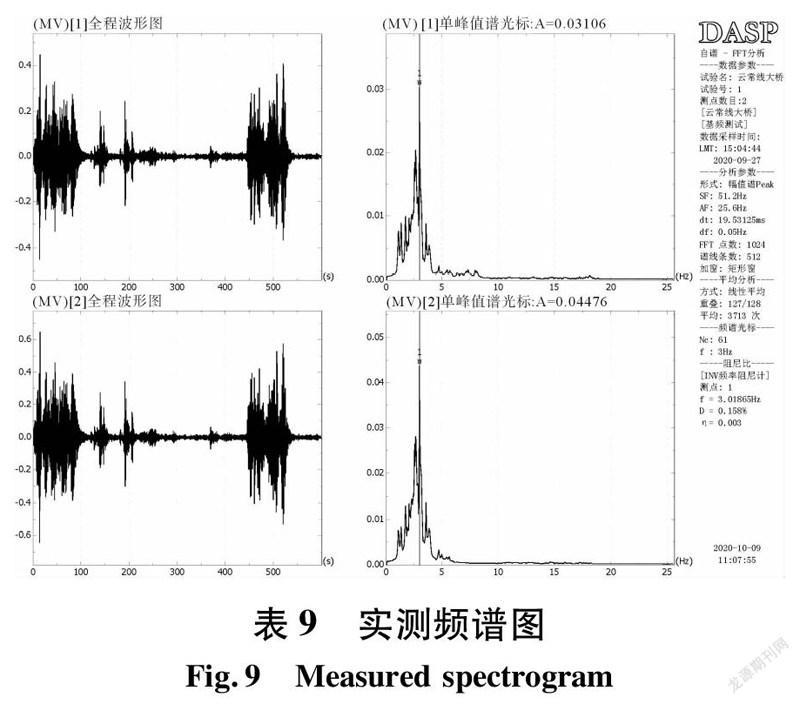
在试验跨1/4跨、跨中分别布置加速度传感器，横断面布设位置为护栏内侧，根据自然环境激励，对桥梁动力特性参数进行识别，分析主梁的振动响应，包括自振频率、阻尼比。主要根据傅里叶变换的谱峰值法，对数据进行自振特性参数分析，采用Coinv DASP V11软件对自振特性参数进行识别，测试频谱图如图9所示。0F6D8556-6ACD-4637-8135-A62BF25AC6C0

由实测结果可知，实测自振基频为3.019 Hz，大于有限元计算值2.174 Hz;实测阻尼比为0.158%，属于桥梁结构正常的阻尼比范围0.08以内。表明结构整体性较强，动刚度较大。

3.2动载试验

为保证激振信号能够达到足够的强度，计算采用1辆载重汽车分别以30、40、50 km/h的时速驶过桥梁，对桥梁进行激振，以测取响应信号;动应变测点布置在Ⅰ-Ⅰ、Ⅱ-Ⅱ截面3^#、4^#梁底板处。

采用Coinv DASP V11软件进行数据结果识别，通过3点法的方法对冲击系数进行计算，在跑车工况中测得主要截面的最大动应变与相应的静应变，进行计算，得到冲击系数，结果如表4所示;每个控制截面测点动应变时程曲线如图10所示。

在跑车动载激励下，桥梁试验跨I-I截面、II-II截面的冲击系数计算平均值分别为为0.053、0.050，根据《公路桥涵设计通用规范》计算的冲击系数为0.121，实测值小于计算值，表明桥梁结构整体平顺，在行车激励下主梁结构整体振幅较小。

4结语

（1）在相当于设计汽车荷载效应的车辆荷载作用下，各工况主要测点应变校验系数0.63～0.98;主要测点应变相对残余均小于20%;各控制主梁截面腹板测点应变基本上呈三角形线性分布，表明主梁应力状况符合设计要求。按照95%的置信度进行区间估计，该桥的挠度校验系数在0.62～0.81，表面结构刚度具有足够的安全富余度，满足规范和行车要求;

（2）根据动载试验，桥梁实测基频大于计算基频，实测阻尼比為0.158%，满足规范要求，试验跨的实测冲击系数均小于计算值，表面桥梁整体性较强，动刚度较大，同时桥面平顺，行车激励下主梁结构整体振幅较小;

（3）采用图表分析和区间估计，有效排除了因为应变和挠度测点数量多而造成的数据随机性和离散性大的情况，同时精确了校验系数取值范围，为各类桥梁静载试验校验系数的计算分析提供了借鉴意义。

【参考文献】

[1]郑一峰，雷刚.城市桥梁技术状况评定及动静载试验研究[J].甘肃科学学报，2021，33（2）：101107.

[2]谌润水， 胡钊芳. 公路桥梁荷载试验[M]. 北京：人民交通出版社， 2003.

[3]宋一凡. 公路桥梁荷载试验与结构评定[M]. 北京：人民交通出版社， 2002.

[4]郑继光， 孙福申， 李煜，等. 混凝土桥梁结构工后评价及其方法[J]. 吉林交通科技， 2000（3）：2931.

[5]陈栋梁. 桥梁技术状况评定方法比较研究[D].重庆：重庆交通大学，2013.

[6]陈树礼，刘永前.城市与公路桥梁技术状况评定方法对比分析[J].建筑科学与工程学报，2018，35（3）：95103.

[7]宋永焕，韩帅，袁浩，等.基于《公路桥涵养护规范》与《公路桥梁技术状况评定标准》的桥梁技术状况评定结果对比分析[J].交通标准化，2012（2）：3337.

[8]彭松.现行公路桥梁技术状况评定标准优化研究[J].公路与汽运，2020（5）：117119.

[9]长安大学. 公路桥梁荷载试验规程[M]. 北京：人民交通出版社股份有限公司， 2016.

[10]王梓坤. 概率论基础及其应用（第2版）[M]. 北京：北京师范大学出版社， 1996.0F6D8556-6ACD-4637-8135-A62BF25AC6C0