基于PIV试验示踪粒子添加方式的研究
邱奕龙 陈荟宇 曾鸿基 吉雷
1.中国石油西南油气田公司天然气研究院 2.中国石油天然气集团公司天然气质量控制和能量计量重点实验室 3.西华大学流体及动力机械教育部重点实验室
随着计算机和处理图像技术的飞速发展,利用集流动可视化和流动测试一体的PIV(Particle Image Velocimetry)技术成为了研究流场特性的新兴方向[1-2]。
PIV技术为一种利用弥散在流体中的粒子对光的散射作用,用光学方法测得粒子在流场中不同时刻的位移,并基于粒子的跟随性来确定流场的各种参数的技术[3],相比于其他测试流场的方式,大大降低了对流场本身的扰动。倪锐等[4]利用PIV技术对天然气管道内流场进行测量,发现PIV技术测量误差很小,符合实际要求。而加注示踪粒子是PIV测量的前提条件,示踪粒子的添加方式对流态扰动有不同影响,内部示踪粒子分布也不尽相同。马昌友等[5]通过PIV对暂冲式风洞高亚音速平面叶栅流场进行测量时发现了示踪粒子越大对流动的跟随性越差;陈莹等[6]在低速风洞中完成了对PIV示踪粒子最佳投放位置的研究。应用PIV技术测量流场时,示踪粒子加注方式对流场和示踪粒子质量浓度的分布存在影响,对示踪粒子加注方式的研究十分必要。
为了更加深入地探索示踪粒子的加注方式对流场及质量浓度分布的影响,设计了3种示踪粒子加注方式,并比较对流场的扰动情况和粒子的分布规律,得到最优加注方式,为PIV测量技术提供理论指导。
1 理论
流体在流动过程中遵循连续性方程和动量方程。
连续性方程即流入控制体内的净质量流量与控制体内由于密度变化在单位时间里所增加的质量相等[7],连续性方程的理论公式如式(1)所示[8]。
(1)
式中:ρ为气体密度,kg/m3;t为时间,s;u、v、w分别为流体沿x、y、z3个方向的速度,m/s。
动量方程即一个系统不受外力或所受外力之和为零[8],这个系统的总动量保持不变,理论公式如式(2)~式(4)所示[9]。
(2)
(3)
(4)
式中:P为流体所受压力,Pa。
本次模拟采用的颗粒模型为液滴,粒径为1×10-6m,质量流量为1×10-20kg/s。由于在实际试验过程中,颗粒将会受到流场中的拖曳力、浮力、压力梯度力和虚拟质量力,其颗粒在拉格朗日坐标系下所受到的力学平衡方程如式(5)~式(8)所示[10]。
(5)
(6)
(7)
(8)
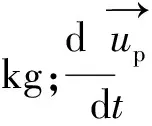
2 数值模型
2.1 几何模型
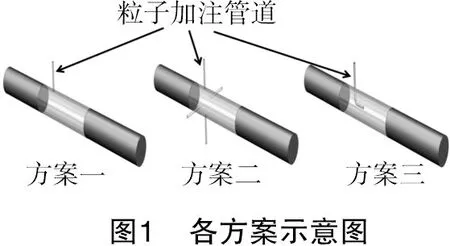
本次数值模拟使用NX10.0软件对几何模型进行绘制,天然气主管流道为直径100 mm、长度5 000 mm的圆柱形流道,采用3种方案对示踪粒子进行加注,加注位置均为距主管流道入口800 mm处。方案一为单旁通管道加注粒子;方案二为四旁通管道加注粒子;方案三为L型管道加注粒子。各方案模型示意图如图1所示。
2.2 网格模型
对几何模型进行网格划分是所有CFD的基础,网格划分的意义在于将连续的流体利用网格块离散化[10]。本次数值模拟对3个方案的模型进行了网格划分,并对其进行了网格无关性验证,当网格数量为3 282 718时,所有方案的监测点物理量均不随网格数增加而改变,本研究的所有模型的网格数量均大于3 282 718。
2.3 计算模型
采用FLUENT进行数值模拟,湍流模型standardK-ε,近壁面函数选择Standard Wall Functions,流体介质为甲烷,主管道入口采用速度入口,流量为100~600 m3/h,出口为压力出口,壁面采用光滑无滑移壁面。压力速度耦合采用SIMPLEC算法,空间离散模型除了Gradient采用最小二乘法,其余均为二阶迎风格式。选择液滴作为示踪粒子,粒径为e-6m,为了更加贴合真实粒子加入管道中,在DPM模型中采用粒子与流场耦合的方式求解粒子颗粒的轨迹,并假设粒子在流场中受到剪切力、压力梯度力和虚拟质量力。
3 结果分析
3.1 不同添加方式对流场湍流强度的影响分析
湍流强度是表征流场微观脉动特征的重要参数之一,它是速度波动的均方根与平均速度的比值,在探究管道内流场的流动特性时,需要着重关注流场内的湍流强度,当湍流强度小时,流场即趋于稳定[11]。
湍流强度计算公式如式(9)所示。
(9)
式中:I为湍流强度,无因次。
本次数值模拟应用上述数值模型,应用 FLUENT软件,对3种方案在各个进口流量下的流场内湍流强度进行了计算,绘制了不同方案对流场湍流强度影响的单线图(见图2)。
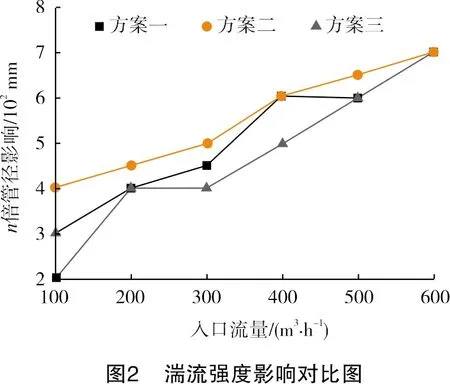
如图2所示,在大流量600 m3/h 时,3种方案对流场湍流强度的影响均在7倍管径以内,小流量100 m3/h时,方案一对流场湍流强度的影响最小,而当流量大于200 m3/h 后,方案二对流场湍流强度的影响略大于方案一、方案三。
这是由于单管加注相比多管加注时,示踪粒子仅从一个方向进入,减少了对流场截面上流体整体的扰动,而相比于L型管的加注方式,单旁通管并未过多地伸入流场内部,所以其扰动也小于L型管加注方式。而当入口流量开始较大时,这些影响开始变得可以忽略,所以方案一优于方案二、方案三。
3.2 不同添加方式对流场涡量的影响分析
旋涡是流体中非常常见的一种运动形态,涡量是描写旋涡运动的物理量,为流体速度矢量的旋度[12-13]。涡量动力学方程是反映旋涡流体变化规律的方程,如式(10)所示[14]。利用该方程可说明流体中旋涡的产生、变化现象,且涡量越小时,流场越稳定。
(10)
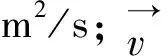
使涡量发生变化的因素有质量力、压强梯度、黏性应力、流体压缩或膨胀、涡线变化等[15],本次试验中3种示踪粒子的加注方式必然对原流场产生扰动影响。为此,应用FLUENT软件,对3种方案在各个进口流量下的流场内涡量分布进行了计算(见图3)。
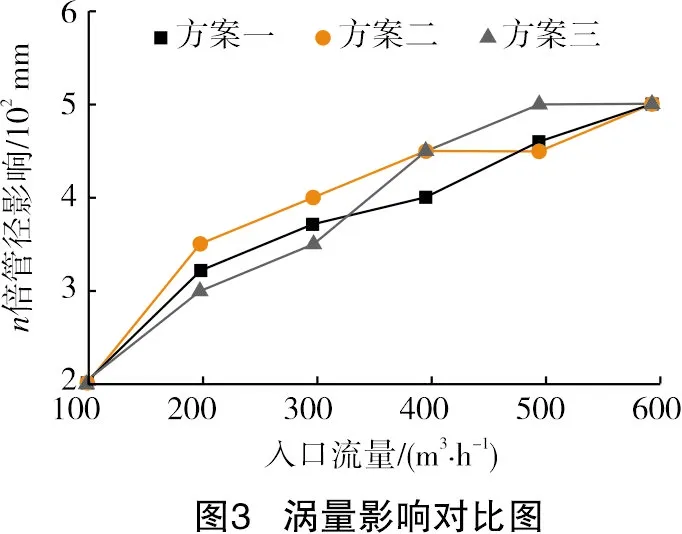
由图3可以看出,3种方案在各种流量下对流场涡量的影响均在5倍管径以内。当流量在300 m3/h以下时,方案三对流场的涡流影响小于方案一、方案二,这是因为方案三的示踪粒子是顺着流场流动的方向而释放出的,所以示踪粒子与天然气的流动方向从一开始就相同,这就使得流场的涡量变化没有方案一、方案二那么大。而当流量大于300 m3/h后,由于L管的管壁直接伸入到管道内部,流量大时对管壁的击打程度大,此时方案三对流场涡流的扰动略大于方案一、方案二。
3.3 不同添加方式粒子质量浓度分布情况的分析
PIV技术是通过采集管道内示踪粒子在CCD相机两次曝光的位置,利用位置差除以曝光时间求得速度,进而求得和速度有关的其余物理量[16]。因此,要得到完成的流场结果,其示踪粒子在管道内的分布必须均匀,为此,对不同添加方式的示踪粒子质量浓度分布进行了对比。
图4为不同加注粒子方式的质量浓度分布图。由图4可知,方案二的示踪粒子分布最好,各处较为均匀,方案一次之,方案三的粒子几乎全部分布于管道中部。造成这一现象的原因是方案一和方案二的示踪粒子在加注时存在与主流场速度方向垂直的速度,且粒子在y方向行驶的过程中,直到主管底部粒子y方向速度仍不为0,故颗粒在流场的剪切力作用下,会布满整个管道;方案三的示踪粒子分布主要集中在管道中心位置,管壁附近颗粒质量浓度较低。这是由于L型管道的粒子出口y方向速度很小,且主管道的流速也较小,湍流强度不高,以至于颗粒无法到达管壁附近,造成粒子分布不均的现象。
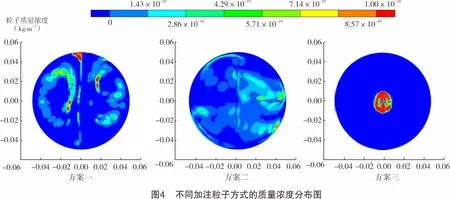
由图4可以看出,方案二的粒子分布最好,各处较为均匀,方案一次之,方案三的粒子几乎全部分布于管道中部。由于方案一和方案二的示踪粒子在注射时存在与主流场速度方向垂直的速度,且粒子在y方向行驶的过程中,直到主管底部粒子y方向速度仍不为0,故颗粒在流场的剪切力作用下,会布满整个管道;方案三的示踪粒子分布主要集中在管道中心位置,管壁附近颗粒质量浓度较低。这是由于L型管道的粒子出口y方向速度很小,且主管道的流速也较小,湍流强度不高,以至于颗粒无法到达管壁附近,造成粒子分布不均的现象。
3.4 试验
为验证数值计算的准确性,对四管加注示踪粒子的方式进行了试验,试验在国家石油天然气大流量计量站成都分站和西华大学流体与动力机械教育部重点实验室进行。实际试验过程中,采用PIV设备对天然气管道示踪粒子添加方式进行了研究,实验设备见图5~图6。

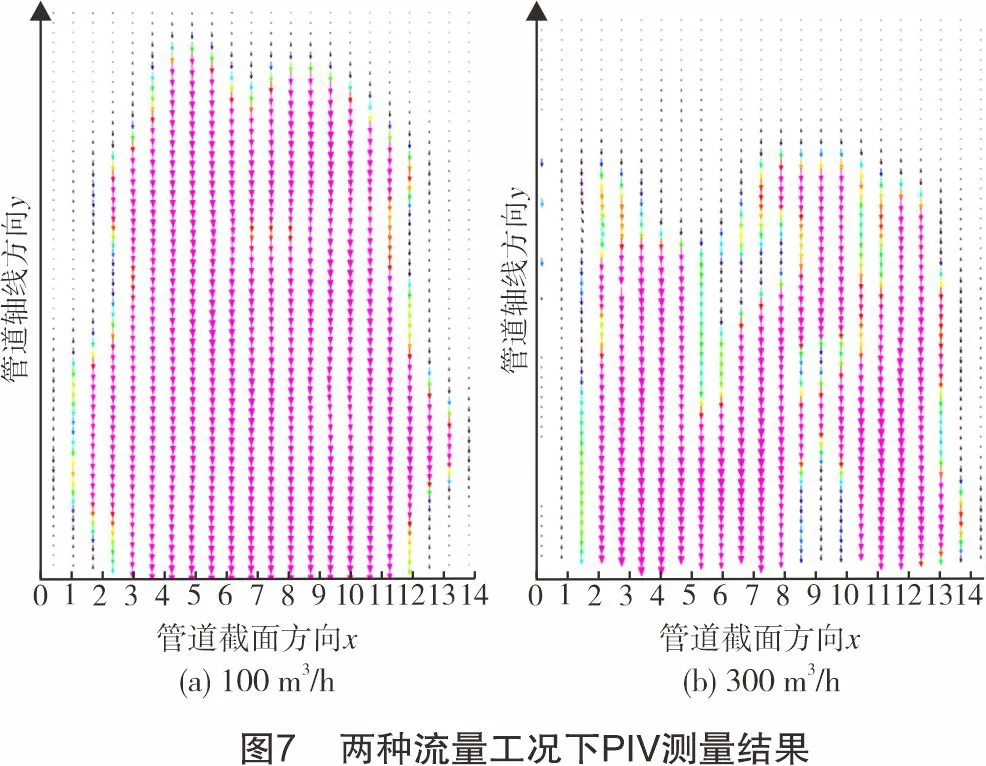
试验中将透明管设置在距加注口10倍管径(10d)处,通过粒子成像测速仪进行测试,由PIV高速CCD相机获取粒子速度矢量图,试验压力1.5 MPa,试验温度31 ℃。从两个流量工况来看,天然气流速矢量箭头方向一致,没有明显漩涡,表明此处流体流动平稳,上游示踪粒子加注对下游流态的影响已基本消弭;整个测量区域均存在粒子速度矢量,说明示踪粒子分布可布满管道。该结果与数值计算结果相符,证明了此次数值模拟的可靠性。图7所示为PIV测试结果。

4 结论
(1)单管加注示踪粒子在小流量下对流场的影响较小,随着流量的增大,对流场的影响程度增大;多管加注示踪粒子在大流量时对流场影响与单管加注差异不大;L管加注示踪粒子在各流量下对流场的影响均较小。
(2)L型管道加注示踪粒子时,粒子在管道内的分布极不均匀,几乎全部集中于管道中部,所以不宜用于PIV测量,容易造成误差,而多旁通管道注射示踪粒子后粒子在管道流场内的分布最为均匀。
(3)通过PIV装置对四管加注示踪粒子的方式进行了验证,试验结果显示,天然气流速矢量箭头方向一致,没有明显旋涡,表明流体流动平稳,上游示踪粒子加注对下游流态的影响已基本消弭;整个测量区域均存在粒子速度矢量,表明示踪粒子分布可布满管道。该结果与数值计算结果相符,证明数值模拟的可靠性。
综上,多旁通管道注射示踪粒子为天然气管道内流场最优示踪粒子加注方案。

