基于“轨迹坐标”的竞赛小车凸轮设计

梁国栋，霍海涛，王 怡，石纪新

(1.天津科技大学工程训练中心，天津 300222；2.天津科技大学教学质量监控与评估中心，天津 300222；3.天津科技大学机械工程学院，天津 300222)

中国大学生工程实践与创新能力大赛是列入《教育部评审评估和竞赛清单(2021年版)》(教政法厅函〔2021〕2号)的重要赛事[1].大赛里工程基础赛道中的势能无碳小车和热能小车绕障行驶竞赛项目，绕障的难度逐届增加，从早期的“8字形轨迹”“直道S形轨迹”，逐步提高为“双8字形轨迹”“环道S形轨迹”，直至2021年的新“环形轨迹”和新“8字形轨迹”，每次竞赛的绕桩难度较上一次都明显提升，导致绕桩轨迹越来越复杂.实际上，轨迹的变化对于小车的最根本影响是凸轮轮廓的变化.为了设计出满足竞赛小车运行轨迹要求的凸轮，本文介绍一种基于“轨迹坐标”的竞赛小车凸轮设计方案.文中所述凸轮机构的设计方法，能够全面应对赛题避障轨迹的变化[2]，解决有各种避障运行轨迹要求的小车凸轮的复杂设计问题，具有很强的适用性.

1 比赛规则对设计的要求

赛场为5200mm×2200mm 的长方形平面区域，赛场中间设有隔板，隔板与边框之间区域即为赛道，在赛道中心线上放置有障碍桩(如图1的运行方式示意图中所示的圆点)，障碍桩为直径20mm、高200mm 的圆棒，障碍桩从出发线开始按平均间距1000mm 摆放[3].

无论是重锤驱动的无碳势能小车，还是斯特林发动机驱动的热能小车，都有环道S形、8 字形和综合3种运行方式.其中：环道S形为在赛道上走S轨迹，如图1(a)所示；8字形为在赛道上走8字S轨迹，如图1(b)所示；综合则为在赛道上交替完成环道S形和8 字形两种轨迹运行方式[3].

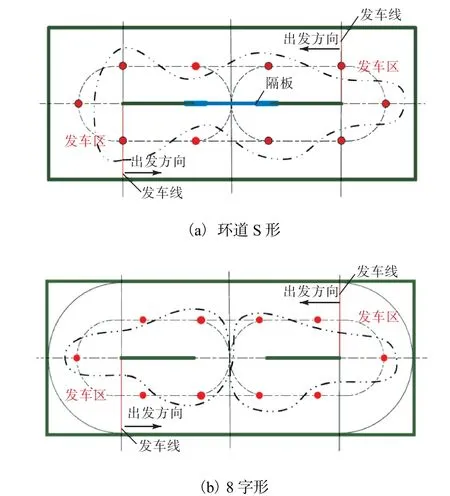
图1 运行方式示意图 Fig.1 Schematic diagram of running mode

本文以环道S形运行方式的比赛规则为例，介绍如何利用计算机辅助设计软件，通过取得规划轨迹上的采样坐标，进行轨迹上各点曲率半径的计算，进而获得凸轮轮廓上各点的坐标，采用“坐标法”开展小车凸轮轮廓设计.

2 运行轨迹的规划

对于2021年赛题设置的复杂障碍题目，如果采用传统方法(设法找到规划轨迹曲线的函数或者利用几个已知函数曲线拼凑规划轨迹并求得轨迹曲率的方法)进行复杂轨迹映射凸轮轮廓线的设计，将很难完成设计任务.一方面，很难找到与规划轨迹完全一致的曲线函数；另一方面，为了让规划的轨迹尽可能贴近已知的函数曲线，就要降低规划轨迹的相关技术指标，损失轨迹曲线的优化程度.

在三维可视化实体模拟软件Autodesk Inventor中，可以在没有确切轨迹函数的情况下，按照比赛规则要求确定的赛道布局图，进行主动轮避障运行轨迹规划和施画，结果如图2所示.在草图环境中[4]，用鼠标从任意一点拉动轨迹曲线，在满足避障约束条件的情况下，不断调整各部分轨迹曲线的曲率变化至合适位置，使之尽可能平滑，同时还要考虑轨迹规划的总路径长度要与主动轮的直径和周长、传动比等小车的主要参数相匹配.

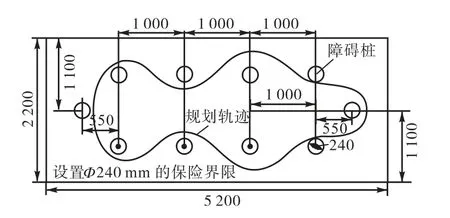
图2 Inventor中的环道S形避障轨迹规划图 Fig.2 “S-shape in loop” trace roadmap in Inventor

在Inventor中确定好主动轮的运行规划轨迹之后，将轨迹图导出为DWG格式，随后导入到AutoCAD中，再将主动轮轨迹向外扩展一定距离(主动轮与导向轮中心的距离)，即得到后轴中点P的运行轨迹，结果如图3所示.

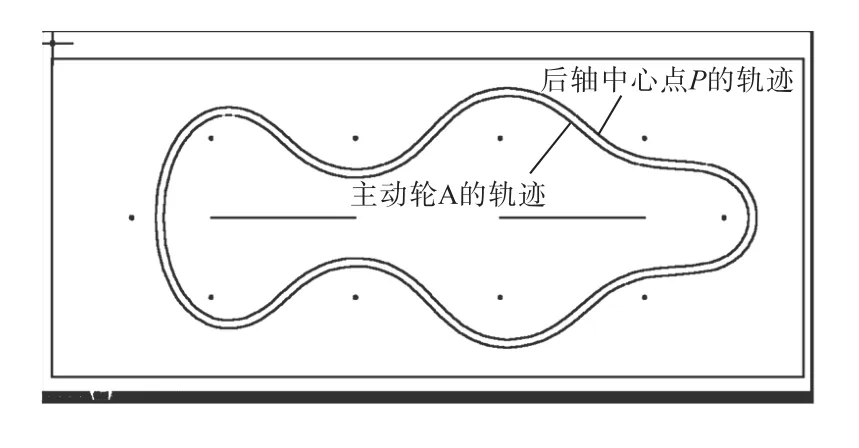
图3 环道S形避障轨迹规划CAD图 Fig.3 “S-shape in loop” trace roadmap in CAD

在AutoCAD中的P点运行轨迹图上，等间隔设置360个轨迹采样点，通过AutoCAD 中的“数据提取”功能，取得并导出每个采样点在世界坐标系中相对系统默认原点的各点坐标[5].采样点位置坐标示例见表1.

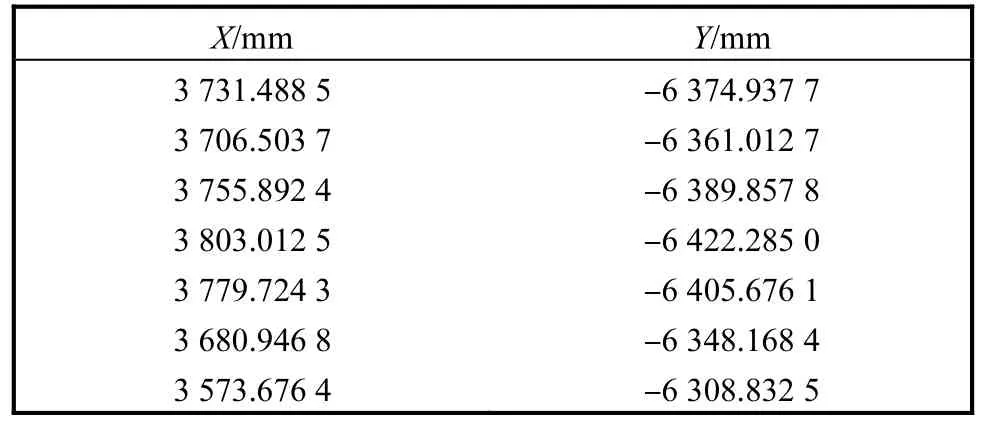
表1 规划轨迹上的采样点坐标示例 Tab.1 Example of coordinates of sampling points on the track

3 结构参数与轨迹参数的假设与确定

3.1 小车部分结构名称与参数

小车运行示意图如图4所示.

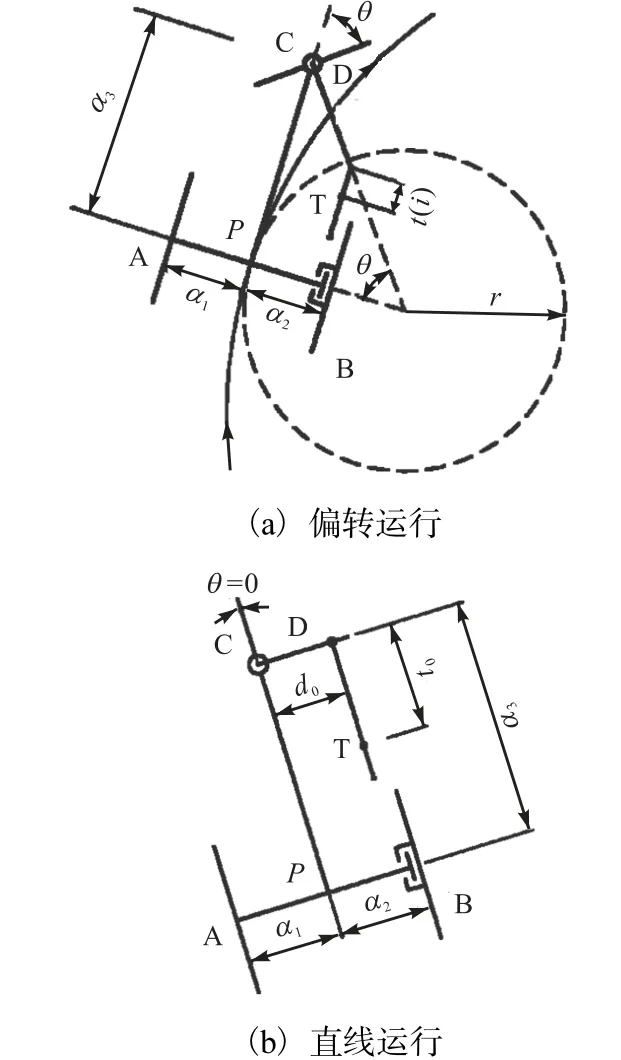
图4 小车运行示意图 Fig.4 Schematic diagram of running car

图4中：A为小车的主动轮(左后轮)；B为小车的从动轮(右后轮)；C为小车的导向轮(前轮)；D为转向杆，转向杆的高度与凸轮的基圆圆心保持水平；T为转向控制凸轮，凸轮设计在从动轮一侧.P为后轴中心点；α1为主动轮与导向轮中心的距离，α2为从动轮与导向轮中心的距离，α1＝α2＝55mm；α3为导向轮中心与后轴水平中心的距离；θ为导向轮的转向偏角，如图所示前进方向，向右偏转为“＋”，向左偏转为“－”；t0为导向轮偏转角为0°时，凸轮基圆中心与导向轮中心的距离，也是凸轮基圆半径；t(i)为凸轮每转过1°时的凸轮向径；d0为导向轮的中心与凸轮厚度中心在X轴方向的距离；r为采样点处的轨迹曲线的曲率半径.

3.2 求解转向偏角变量

与小车的运行轨迹和转向控制凸轮的轮廓线都有关联的变量是导向轮的转向偏角θ.小车的导向轮的转向偏角θ和运行轨迹是一一对应的，同时导向轮转向偏角θ的偏转大小受到与凸轮和导向轮相连接的转向杆的控制.凸轮向径t(i)对转向杆产生的推程与导向轮的转向偏角θ也是一一对应的.因此，转向偏角θ是凸轮设计过程中的主要变量之一，由图4分析可知：

θ＝0°时，小车沿直线方向运行.

3.3 轨迹曲线任意一点处曲率半径的求解

在曲线上的某个点处的微小区域，可以找到一个与其曲率相等的圆，该圆的半径就是曲线上该点处的微小区域的曲率半径[6].

也可从微分的角度理解，就是尽可能地把一段曲线微分，直到最后近似为一个圆弧，此圆弧所对应的半径即为曲线上该点的曲率半径[7].

轨迹曲线上每个采样点位置都存在曲率半径r，r是凸轮设计过程中的主要变量之一.在取得的360个轨迹采样点的坐标中，通过依次选取相邻的3个采样点的坐标，可以计算出每个采样点的曲率半径.

假设轨迹上相邻的3个采样点坐标分别为(X1，Y1)、(X2，Y2)、(X3，Y3)，设(X2，Y2)对应的曲率半径为r，对应圆心坐标为(X0，Y0)，位置关系如图5所示.

硅质岩中的Al2O3和TiO2可用于判别大陆边缘沉积环境，Fe2O3可反映大洋中脊组分的影响强度[3]。样品中SiO2/Al2O3比值为9.82～62.43，比纯硅质岩(SiO2/Al2O3比值为80～1400)低很多，SiO2/Al2O3比值和Al2O3呈较好的负相关关系(图2b)，且TiO2含量为0.026%～0.386%，Al2O3/TiO2比值为14.69～73.83，与Al2O3具有较好的正相关关系，均表现为富铝特征，表明研究区有陆源碎屑沉积物[16]。

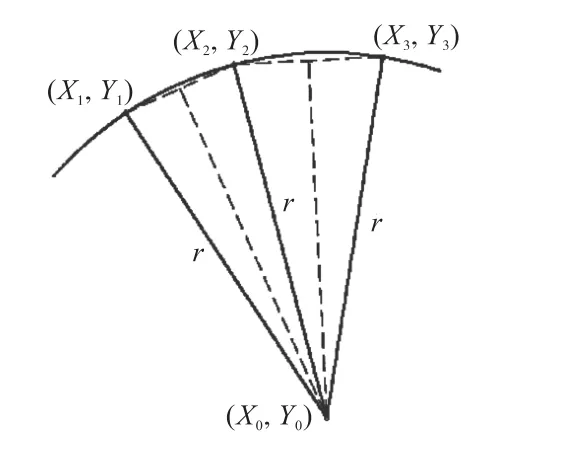
图5 轨迹上相邻三点坐标 Fig.5 Coordinates of adjacent three points on track

依据图5中关系，可列出如下方程：

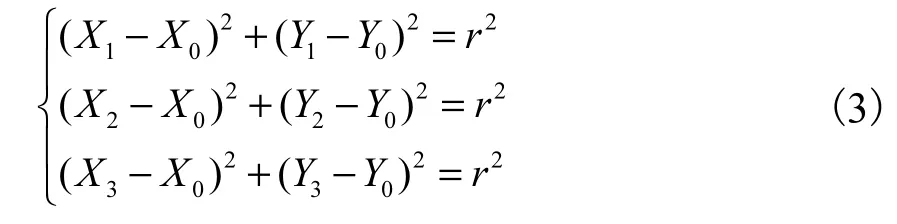
解这个方程组可得出圆心坐标(X0，Y0)的具体数值，进而可计算得到曲率半径r.

由于运算量比较大，使用Microsoft Visual C++制作了曲率半径计算工具(如图6所示)，应用该计算工具可节约大量计算时间.

图6 轨迹采样点曲率半径的计算工具 Fig.6 Radius of curvature calculation tool for sample points on track

将360个采样点的曲率半径计算结果按照X坐标顺序进行列表，结果见表2.

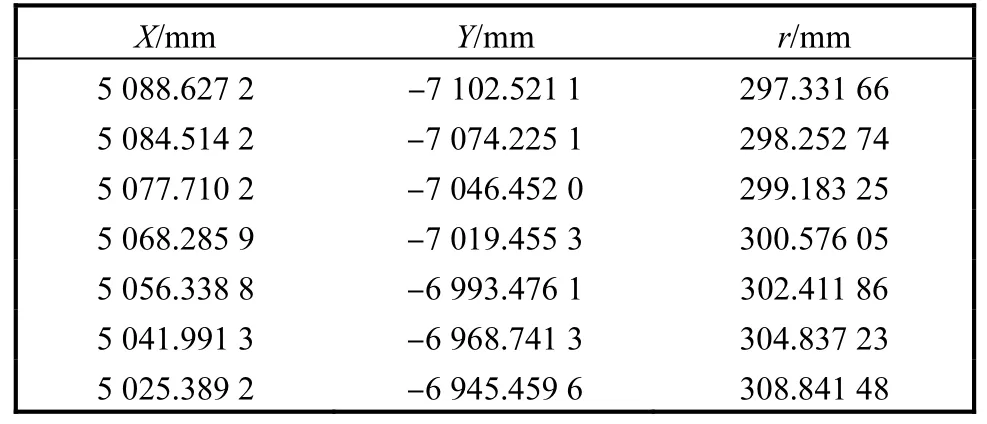
表2 采样点曲率半径计算结果示例 Tab.2 Example of radius of curvature calculation results for the sampling points

3.4 凸轮坐标参数的确定

凸轮的向径是凸轮回转中心与推杆之间的距离，也就是凸轮轮廓边沿上某一点距离凸轮回转中心的长度[8].通过图4中小车与转向凸轮推杆的受力与运动状态分析和解析计算，可计算得到凸轮向径.

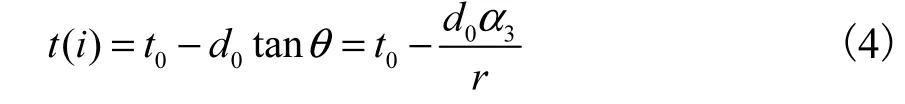
凸轮旋转一圈对应小车行走一个周期的轨迹，以1°为分度，凸轮每转过1°找到对应轨迹上的一点.按照此操作，将凸轮旋转的一周均匀地分成360份，每一份看作1°[2].在一个周期的轨迹运行过程和一个凸轮旋转周期(0°～360°)中，轨迹上选取的360个点的坐标与凸轮转角的每1°相对应.通过确定每1°对应的凸轮向径，可计算得到凸轮轮廓上对应点的坐标(Tx，Ty).

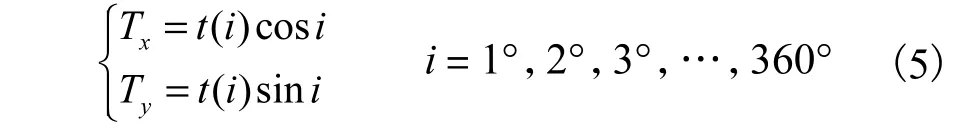
通过式(5)计算可得凸轮轮廓上点的坐标，示例见表3.

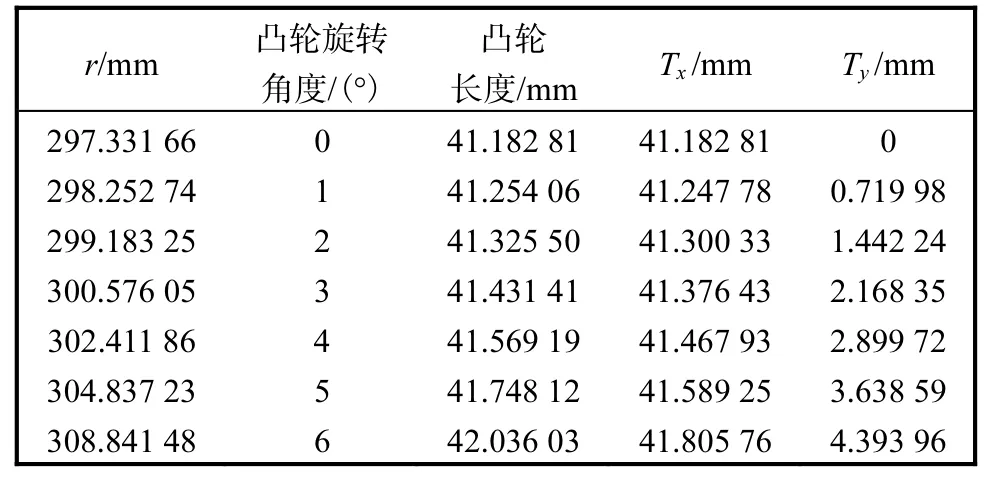
表3 凸轮轮廓上点的坐标计算结果示例 Tab.3 Example of coordinate calculation resultswith points on cam profile

4 凸轮的生成

将计算出的凸轮轮廓上点的坐标用Excel软件整理成坐标列表，然后导入AutoCAD软件中，生成凸轮轮廓的二维曲线图，结果如图7所示.

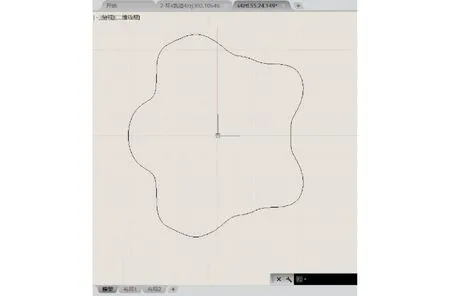
图7 凸轮轮廓的二维曲线图 Fig.7 Two dimensional curve of cam profile

将在AutoCAD中生成的凸轮轮廓的DWG文件导入三维软件UG NX中进行拉伸建模[9]，生成凸轮轮廓三维建模图(图8)，该图可用于凸轮的加工制造.凸轮厚度设计为3mm.

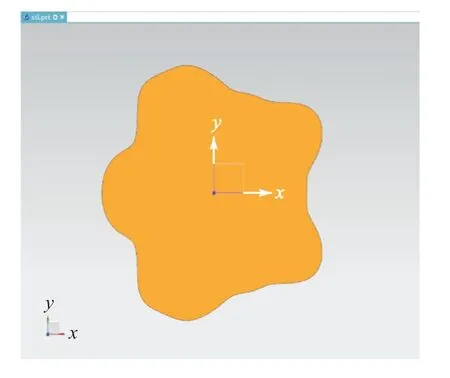
图8 凸轮轮廓三维建模图 Fig.8 3D modeling diagram of cam profile

本方案的凸轮轮廓线是依靠映射小车运动轨迹的方法获得的.为了保证作为摆动从动件的推杆的运动规律平稳，在确保小车能够通过比赛规则规定的障碍物的情况下，需要通过采用调整小车的规划轨迹的方法找到一条轨迹，使通过该轨迹映射获得的凸轮轮廓线平滑无死角.

通过观察可知，设计出的凸轮轮廓线整体没有出现锐角和直角，内外转角均能够平滑过渡，有利于提高运行轨迹与设计轨迹的拟合度和推杆的平稳运动，设计合理.

将本文设计的凸轮加工成型，并与其他零件一起组装成热能驱动小车，该小车的实物图如图9所示.

图9 热能驱动小车实物图 Fig.9 Photo of thermal energy-driven trolley

5 运动轨迹仿真

将小车的α1、α2、α3、t0、θ、r、S等参数及坐标代入MATLAB程序，对后轴中点P的运行轨迹进行仿真，得到仿真轨迹如图10所示.

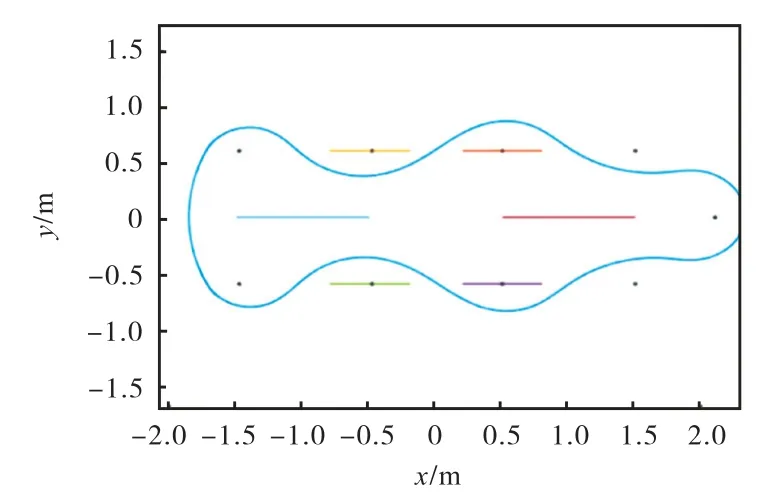
图10 后轴中点P的MATLAB仿真运行轨迹 Fig.10 Simulation of running track for midpoint Pin MATLAB

仿真结果表明，小车运行时不会与障碍桩、隔板和边框发生触碰，可实现有效避障，小车轨迹规划合理，参数选择适当.

如果要得到更高的轨迹拟合度，可以采用提高轨迹采样点数量和对应的凸轮一周均分份数的办法.文中设计时使用的360均分法，无论是在仿真过程中，还是在制作的凸轮的实际运行过程中，其结果均验证了此数量能够满足使用要求.

6 结 语

本文以2021年中国大学生工程实践与创新能力大赛基础赛道的环道S形运行方式的运行轨迹为例，利用在规划轨迹路径上的采样坐标，采用轨迹中相邻三点的坐标计算出中间点处曲率半径，运用规划、分析、计算、归纳和仿真等设计手段，介绍了一种能够普遍适用于各种运行轨迹的凸轮设计方法.该设计方法区别于传统设计思路，综合运用了多种强大设计工具软件中的简单功能，相互组合接力，解决了小车用于各种避障运行轨迹的凸轮的复杂设计问题.采用此设计方案制作凸轮的势能小车和热能小车，在天津赛区的竞赛中取得了一等奖的成绩.该研究结果对于全国性竞赛项目中的该类型竞赛题目的解答有十分重要的参考意义.该凸轮的设计方法，对于其他机构，尤其是带有凸轮的机构，也提供了十分有益的设计思路和方向.