欧洲大学数学教育研究发展趋势——基于第十届欧洲数学教育研究学会大会的分析

◎王萍萍 严亚强 (.苏州大学东吴学院,江苏 苏州 5000;.苏州大学数学科学学院,江苏 苏州 5000)

数学教育是一个年轻而蓬勃的研究领域，有学者甚至将其比作尚在襁褓中的婴儿.相比于数学教育，大学数学教育研究则更为年轻,很多研究都是在20世纪90年代后才出现的.在Tall等人《高等数学思维》这一标志性著作出版之后，大学数学教育研究领域就成了一座“富矿”，不断吸引着学者们多角度、多层次地挖掘与开发.

欧洲数学教育研究学会大会(以下简称CERME)由欧洲数学教育研究学会主办.该学会于2010年成为国际数学教育委员会(ICMI)附属的跨国数学教育组织之一,而CERME是其规模最大且影响力最大的活动形式.“大学数学教育”作为大会的主要专题，近些年接收的论文数量大幅提升，关注的课题愈加广泛，研究愈加细致.以下对这些研究进行分析，提炼其中的热点和趋势，以期对我国大学数学教育研究与实践有所启示.

一、近二十年欧洲大学数学教育研究概述

“大学数学教育”从CERME 1起就是大会的主要专题之一.某学者回顾大学数学教育在CERME中的变化发展历程时,将CERME 1-3称为该专题的“早期研究时代”,CERME 4-6称为“高等数学思维时期”,而从CERME 7开始，“大学数学教育时期”正式来临.到了CERME 10时，该专题接收的论文数是CERME 7时的两倍，且在所有专题中接收的论文数最多.可见，大学数学教育研究越来越受到欧洲数学教育研究者的重视，该领域也越发展现出活力.

二、欧洲大学数学教育研究发展趋势

CERME 10正值大会举办二十周年，吸引了世界各国众多数学教育学者踊跃参与，此次会议对定义和塑造未来几十年欧洲数学的教与学起着重要的推动和引领作用.CERME 10中“大学数学教育”专题的论文具有重要的研究价值，研究方向和方法代表着欧洲大学数学教育研究的最新发展趋势.

1.重视中学与大学数学的衔接与过渡问题

中学与大学数学的衔接与过渡已经成为大学数学教育研究领域的一个热点问题.希腊雅典大学学者的研究描绘了一名数学专业一年级学生两个学期完成中学向大学数学过渡的历程.研究者将其视为“人生大事”，并将此过渡历程分为三个阶段：即将从中学毕业的分离阶段,离开中学到大学初始的阈限阶段,以及融入大学的结合阶段.研究者分别在三个不同阶段对学生进行访谈,聚焦社交、学术和数学内容三个维度在不同阶段上的发展变化,以及社交和学术如何相互作用以完成数学内容维度上后两个阶段的过渡.

意大利米兰理工大学的学者则聚焦大一新生预备课程的课堂笔记，对比学生在一道熟悉的程序性问题和一道不熟悉的陈述性问题的记录情况(记什么、怎么记)，了解学生过渡阶段不同的学习层次、状况和习惯.德国明斯特大学的学者则聚焦大一新生在预备课程前后的自我效能感的变化情况，由于学生自我效能感通常与毅力、坚持不懈及成功相关，因此这一调查结果可以在一定程度上反映学生的过渡情况.

还有学者考察大学教师为帮助新生顺利过渡进行的尝试.英国东安格利亚大学的学者关注数学教师为防止一年级学生产生交流认知冲突,在教学评价上采用的策略.研究者使用斯法德有关数学话语的新术语“交流认知冲突”来表示本研究中数学专业一年级学生在数论学习中对“变量”的错误认知和含糊不清的理解,而这种冲突通常是由“变量”在不同数学领域中的多种表征带来的.研究者通过教师访谈和试题分析,发现教师为避免学生用中学时对“变量”的认知来理解数论中的“变量”,在试题的编排次序、试题叙述的语言上都进行了一定的暗示,教师的这些努力都旨在促进学生从中学数学向大学数学的过渡.

2.重视大学数学教师的教学实践研究

教师是课堂教学最关键的因素，许多研究者对大学数学教师的教学展开探讨.爱尔兰国立都柏林大学的学者引用美国数学家匈菲尔德的一句话概述自己的研究内容：“你看到的和没看到的,决定了你做的和没做的”,聚焦教学中的“决策点”,即一节课中需要教师做出教学决策的重要时机.文中分析了决策点对教学的重要性,指出教师拥有的资源(主要指知识)、取向(包括性情、信念、价值观、体验和爱好)和目标决定了教师做出的教学决策.本文的三位作者对自己在数学教学中有关决策点的135条教学记录进行了分析,从中归纳出8种类型的决策点和7种引发决策点的原因.

美国加州大学伯克利分校的学者也探讨了相关问题，研究者将教师干预学生的决策瞬间比作爵士乐的即兴演出，并利用匈菲尔德的TRU数学框架对一位教师的教学干预进行分析与评价.TRU课堂评价框架包含五个维度：数学内容、认知需求、学生的学习机会、学生的身份认同、应用评价.该评价框架最新版本和层次划分如表1所示.研究者指出TRU课堂评价框架可以发展教师的教学并加强教学反思，是促进教师专业发展的有效工具.

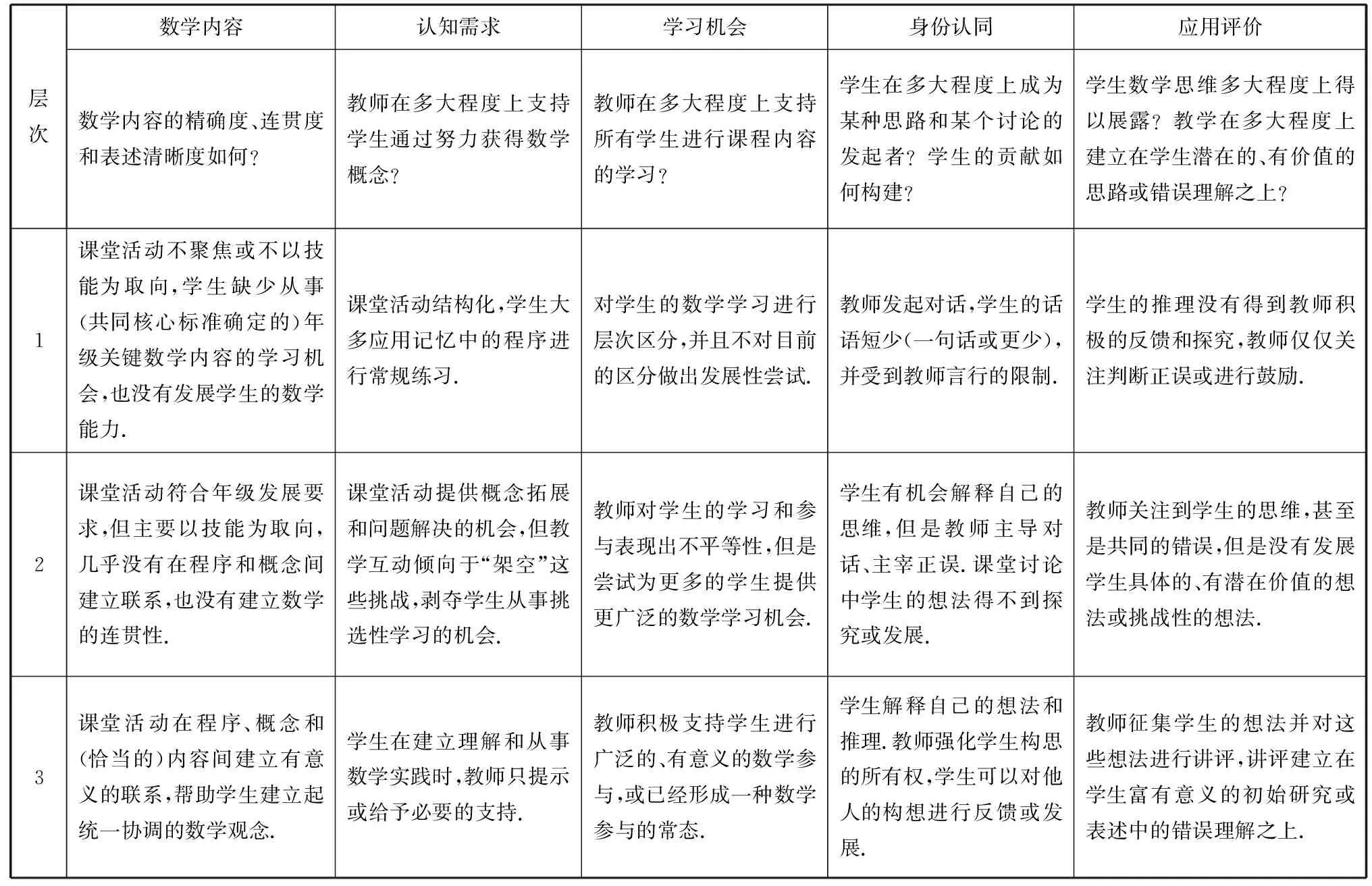
表1 TRU数学课堂评价框架的五个维度

新西兰奥克兰大学的学者通过教师访谈，分析和比较了大学教师的教学情况.研究描述了讲授微积分、线性代数和复分析课程的三名经验丰富的大学讲师对“根”的不同教学理解,并分析了引起这些差异的教学因素,如所教课程传达的数学理念不同,教材所述方法不同,以及讲师对学生进一步学术需求的考虑等.研究者指出,三位讲师传授给学生的知识受到各自所教课程的数学严谨性的影响,他们彼此之间缺乏对话，使得学生对知识的理解受限于教材内容且不全面.研究者呼吁应发展大学数学教师的教学知识，并指出讨论和交流有助于大学数学教师对数学和教学的理解，并建议编制共同认可的定义和概念手册，帮助学生建立连贯统一的数学观念.

3.关注大学生的数学学习情况

了解大学生的数学学习情况是大学教师决定教什么、怎么教、如何改进教学的基础.挪威北极大学的学者调查了自己授课的59名工科一年级学生如何学习线性代数,以及如何检验自己的学习效果.研究者使用扎根理论,将学生的回答分为程序型方法和概念型方法两类.程序型方法指“使用和操作数学技能,如计算、规则、公式、算法和符号等”；概念型方法指“通过解释和应用数学情境中的概念,通过在语言、视觉(图形)和形式数学之间进行转换和连接等表明对概念的理解”.调查显示,学生在学习线性代数时更强调概念型方法，而自己是否学会知识则通过解题,即程序型方法来检验.

数学专业学生的数学学习也是研究者的关注对象，如西英格兰大学的学者调查数学专业二年级学生在“群论”第一学期学习中的体验.数学教学研究中，以抽象代数，尤其是群论为对象的研究并不多见，主要关注学生的认知过程和错误、抽象过程中遇到的困难、学生对语义缩写和符号的反应等.本文研究者以斯法德的交流认知理论为分析框架，考察其他数学领域(如集合论)与群论间交流认知冲突的存在性.通过分析学生的课程作业和访谈等，研究者发现，在处理集合、群、子群及其元素时学生的数学学习是不完善的.此外，研究者还发现即便学生不能完全掌握某个数学概念，也能完成与此相关的数学题的证明.

众多微积分的教学研究都表明，极限概念无论在高中还是大学都是一个难点，它成为学生建立微积分基础、从具体的初等数学思维向抽象的高等数学思维过渡的一大障碍.瑞典斯德哥尔摩大学的学者采用文献分析法，将学生学习极限概念的障碍分为三种类型：与极限的数学根源有关的认识论障碍、与极限的抽象性质有关的认知障碍，以及呈现给学生的教学障碍.研究者指出这三种形式的障碍彼此联系，这些障碍源可以通过教学得以消除.

4.关注大学数学教与学的新方式

众所周知,高等教育正在经历着一场向虚拟教学方式转变的过程,有数据显示,2013年全球有超过四千万高等学院学生接受在线教育,而到2017年这个数据已增至2013年的三倍.美国纽约市立大学的学者就探讨了在线数学教育的有效性.研究者探讨了学生选择在线数学课程的原因、选择在线和面授课程学习成绩的差异等.调查显示,时间限制、与自身性格或学习风格相符是学生选择在线课程最主要的原因；而借助纽约市立大学数据库,研究者发现选择两类不同授课方式的学生在STEM课程的通过率上没有显著差异.研究还显示在线课程会影响学生参与数学课程的模式(内容和顺序等).

英国学者对201名工科大学生在数学学习中使用的工具进行了调查,得到七种类型的工具,分别是“官方”的数学教材、学生的课堂笔记、学校网站上的共享资源、Wolfram Alpha计算引擎、与教师的交流、与同学的交流以及其他网络资源等.显而易见,现代信息和通信技术的发展正在影响和改变着大学生的数学学习方式.

除上述四方面研究外，研究者们还对其他问题展开了探讨，如德国帕德博恩大学的学者研究了一个小型博士生项目中数学助教在数学辅导课程中使用的任务类型；法国布列塔尼南大学的学者采用问卷和访谈方法调查237名法国工程师工作中的数学培训和数学需求；挪威阿格德尔大学的学者展示了生物系学生通过大学数学建模活动在数学观念和数学能力上的变化；塞尔维亚大学的学者通过对一名数学家的推理和证明进行个案研究，从中获得数学教育上的启示.该专题多样化的研究内容展现出大学数学教育领域广阔的探索空间.

三、总结与启示

上述研究至少反映出欧洲大学数学教育研究的以下四个方面特征：

一是聚焦课堂.课堂始终是教育研究的初始地与必然回归，专题中的研究也充分体现了这一点.特别地，许多研究都是大学数学教师身兼教学者和研究者进行的探究，这样的研究更能引发教师产生共鸣，也更能深刻反映并解决教学实际问题.

二是对数学专业师生的关注度提升.以往，关于非数学专业的研究比较多，关于数学专业的研究比较少.CERME 10中有研究者关注数学专业学生从中学到大学数学的过渡、数学专业学生对分析及群论中概念的理解情况，关注教授代数拓扑课程的数学教授的教学日志、数学家在教学中如何进行猜想和证明、数学家和数学教育者合作教数学的项目等，这些研究在一定程度上反映出数学专业领域的教学日益受到研究者关注.

三是重视中学与大学数学的衔接与过渡.研究者围绕此课题进行多层次探讨，如调查大学预备课程中学生的变化、大一学生对数学概念的交流认知冲突、追踪学生大一年级过渡过程的发展变化、关注教师为帮助学生过渡采用的教学和评价实践等，这些研究为更深入了解学生过渡中遇到的困难及制定可行的教学策略提供了丰富的素材.

四是关注大学数学教与学的新方式.科学技术的发展大大改变了现有的大学数学教与学方式，由此带来的一系列相关课题，如教学技术的发展、成效、评价方式等都引起了研究者的关注与重视.

大学数学教育已经成为国内外数学教育研究的一个重要课题,我国学者也进行了广泛而深入的研究.如中学与大学数学的衔接问题上,有的学者对高中与大学数学课堂教学对比，提出若干大学数学教学中存在的问题；有的学者调查分析高中增加与删减内容与学生总体适应性高低的关系;还有的学者从大学数学教材的编制角度提出衔接建议.同时，有些学者关注大学数学课程的设置，如介绍了自己所在大学的数学课程改革及效果、提出大学数学第一和第二课堂进行研究性学习的理念、对大学数学文化课程的建设与教学进行了探索等.近年来，网络教学平台构建、线上线下结合的大学数学教学方式也受到了学者的大量关注.此外，大学数学的教学方式、评价方式,大学生的学习方式、对数学概念的理解等也是学者关注的对象.整体上，就大学数学课程与教学而言，目前已有的研究以非数学专业为主，而数学专业相对较少；关注本科生较多，而关注更高层次的研究生培养、职场数学培训及其过渡问题的不多，显然这些课题都有待更深入探索.