复合受力模式下FRP片材-混凝土界面的受力行为及承载力预测

施嘉伟 徐冰雷

(河海大学土木与交通学院，南京 210098)

纤维增强树脂复合材料(FRP)片材外贴法是目前各类混凝土结构加固修复的一种有效方法[1].将FRP片材外贴于混凝土表面可实现与既有结构的共同受力，并阻止裂缝扩展，从而实现良好的加固效果.FRP片材-混凝土界面是否具有良好的传力性能是影响加固效果的关键，既有研究表明FRP片材加固混凝土平面梁/板易发生始于跨中弯曲裂缝位置处的界面剥离，FRP片材-混凝土界面以纯剪受力(Ⅱ型)为主[2].目前，国内外研究者对FRP片材-混凝土界面的纯剪受力问题已进行了广泛研究，提出的界面黏结滑移模型和界面承载力预测模型能够对纯剪受力模式下的界面受力行为进行较为准确的预测[2-4].

然而，工程应用中通常还存在不少FRP片材-混凝土界面复合受力的情况[5]，如在FRP片材加固混凝土梁中，当混凝土表面出现斜裂缝后相应界面位置处将产生垂直于构件轴线方向的相对错动(Ⅰ型)，表现为复合受力模式(同时存在Ⅰ、Ⅱ 型)；在FRP片材加固混凝土曲面构件(如拱桥、变截面梁桥、隧道衬砌等)中，界面始终处于复合受力状态.相比于纯剪受力模式，复合受力模式下界面除受到面内剪切应力以外，还会受到面外法向应力的影响，受力情况更加不利.

目前已有一些研究者对界面的复合受力问题开展了相关研究.Ghorbani等[6]通过单剪试验，Alam等[7]、Zhang等[8-9]通过双剪试验，研究了复合受力模式下FRP片材-混凝土界面的受力性能，通过设置初始加载角改变界面的复合受力状态，发现随初始加载角的增大，界面受力行为显著改变，极限承载力也随之降低.Zhang等[10]数值模拟了固定加载角下FRP片材-混凝土的界面受力行为，Wang[11]理论分析了复合受力模式下的界面受力行为，Lee等[12]研究了存在界面复合受力模式的FRP片材加固混凝土构件的受力性能，上述研究采用基于幂法准则的起始损伤与失效准则，所得结果能够较好反映复合受力模式下的界面受力行为.Li等[13]采用BK准则研究了动态荷载下FRP片材-混凝土界面的复合受力问题，相比幂法准则，BK准则形式较为复杂，在现有研究中的应用相对较少.目前相关理论和数值模拟研究侧重复合受力模式下界面的受力分析，对界面性能及主要影响参数缺乏定量的模型描述，并且主要考虑固定加载角下的复合受力状况，而在加固构件以及前述单/双剪试验中FRP片材与混凝土之间的加载角是随着界面剥离的扩展而不断变化的，目前缺乏考虑该方面影响的研究.此外，关于幂法准则幂指数的取值不同研究者也不统一，尚缺乏复合受力模式下FRP片材-混凝土界面承载力的有效预测方法.

根据上述分析，本文基于幂法准则对带初始加载角的FRP片材-混凝土双剪试件建立数值模型，在试验验证的基础上进行参数分析，研究初始加载角、幂法准则幂指数、界面黏结滑移参数、FRP刚度、FRP黏结长度等因素对界面受力行为的影响.基于参数分析结果，在既有界面黏结强度模型的基础上考虑复合受力的影响，对其进行修正.最后，利用文献中复合受力模式下界面性能的试验数据，对修正模型预测精度进行了验证.

1 数值模型

1.1 试验

Alam等[7]以初始加载角为主要参数，采用双剪试件(见图1)对FRP片材-混凝土的界面性能进行了试验研究，所得结果反映了复合受力模式下界面受力行为随加载角变化的基本规律.图中，P为试验拉伸荷载，kN；bc=100 mm为混凝土试块宽度，mm；L=300 mm为单个混凝土试块长度，mm；bf=50 mm为FRP片材宽度，mm；a和b分别为台阶水平尺寸和台阶高度，mm.本文以该试验为背景，对更多的参数开展数值模拟分析.试件主体由2块长宽相同而高度不同的混凝土试块构成，通过设置不同的台阶高度b以实现不同的初始加载角，在2块混凝土连接处设置坡度以实现平缓过度.采用环氧树脂浸渍并粘贴碳纤维布于混凝土块两侧，FRP片材理论厚度tf为0.286 mm，FRP片材弹性模量Ef为118 GPa，在非试验段混凝土块外侧缠绕碳纤维布以保证界面剥离破坏发生于试验段.通过试验机夹持预埋钢棒进行加载，试验中台阶处FRP片材首先开始剥离，随加载继续界面剥离逐渐向自由端扩展，直至试验段FRP片材完全剥离.本文通过建立具有不同初始加载角的4组试件的数值模型，验证复合受力模式下FRP片材-混凝土界面数值模拟的可靠性，具体试验参数如表1所示.

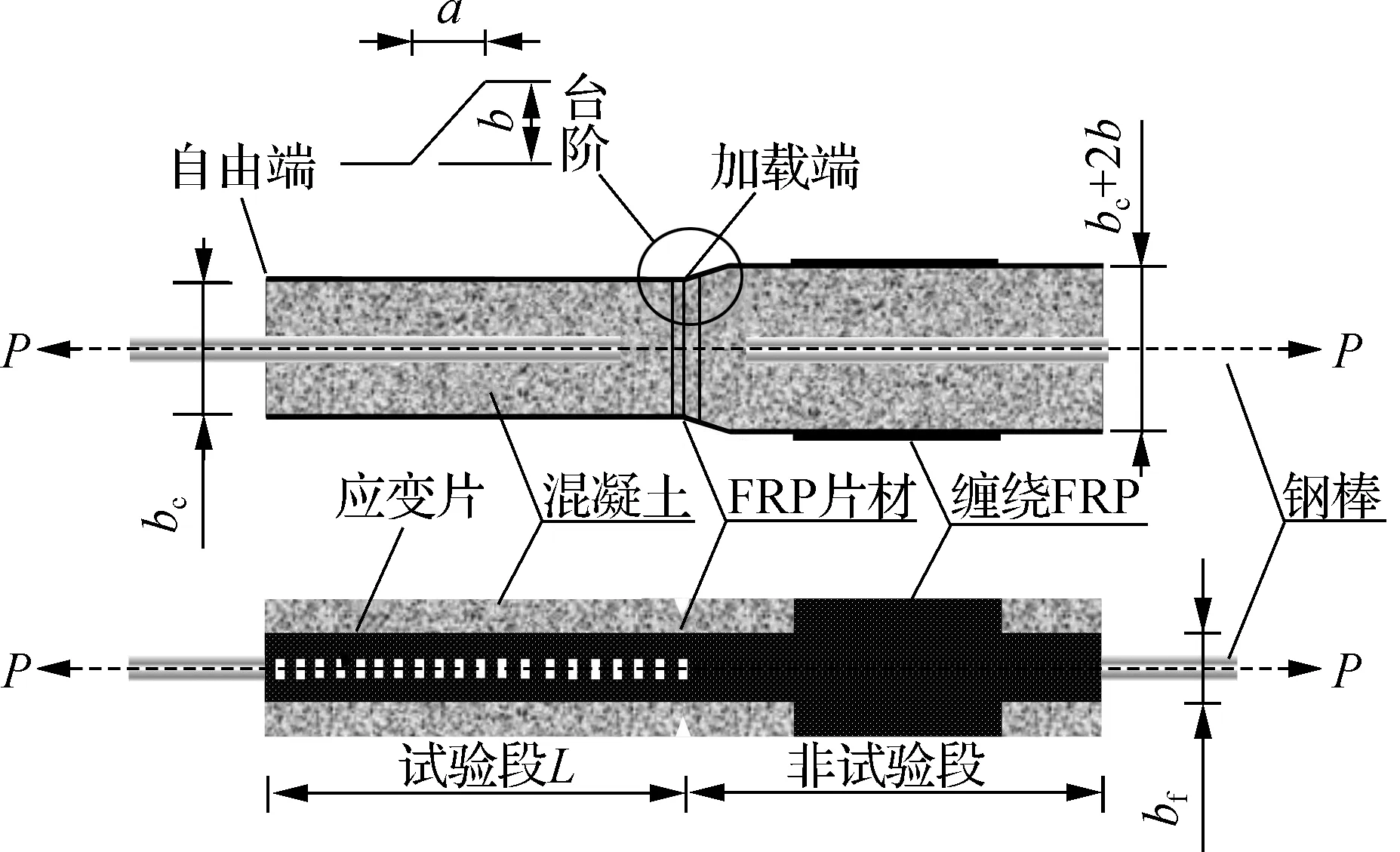
(a) 平面图

1.2 有限元模型

采用有限元软件ABAQUS对双剪试件的试验段建立有限元分析模型，如图2所示.考虑模型对称性，数值模拟采用平面1/2模型，可有效提高计算效率.为便于模拟，在保证FRP刚度Eftf与试验值相同的条件下，FRP片材取单位厚度.参考文献[3-4]，为了便于计算，默认剥离破坏发生于界面层，以界面单元的形式模拟界面受力.混凝土和FRP片材的材性均简化为线弹性，采用平面应力单元进行模拟，FRP片材-混凝土界面采用零厚度内聚力单元进行模拟.混凝土与预埋钢棒网格尺寸为5 mm×5 mm，为准确获取FRP片材的应力情况，将FRP片材网格划分为2层，网格尺寸为5 mm×0.5 mm.

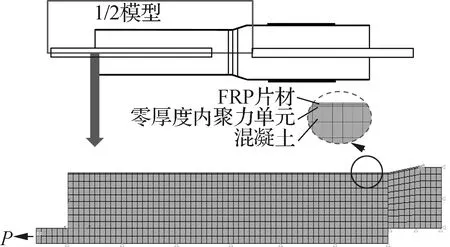
图2 FRP片材-混凝土双剪试件的有限元模型

为了考虑界面复合受力的影响，在内聚力单元属性中分别设置了单向受力时Ⅰ型和Ⅱ型模式下的界面黏结-滑移关系，如图3所示.其中，σ和τ分别为法向和切向黏结应力，MPa；σmax和τmax分别为界面法向和切向局部黏结强度，MPa；ω和s分别为法向和切向滑移，mm；ω0和s0分别为σmax和τmax所对应的滑移，mm；EⅠ和EⅡ分别为界面法向和切向黏结刚度，MPa，即黏结-滑移曲线上升段斜率；GfⅠ和GfⅡ分别为界面法向和切向断裂能，N/mm，即黏结-滑移曲线与横坐标围成的面积.

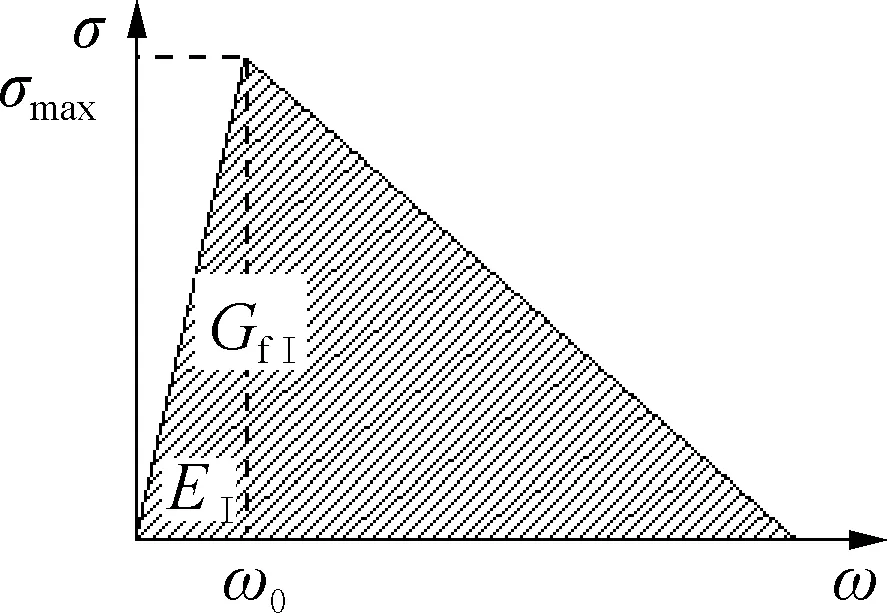
(a) 法向受力(Ⅰ型)

参考文献[14]，Ⅰ型黏结-滑移关系取双线性模型表示，σmax取为混凝土抗拉强度ft，GfⅠ取0.1 N/mm，EⅠ与EⅡ取值相等.Ⅱ型界面黏结-滑移关系及关键参数取值主要参考文献[4]，为了便于ABAQUS软件中内聚力单元属性的参数输入，Ⅱ型界面黏结-滑移曲线上升段简化为直线，表达式如下：

(1a)

(1b)

s0=0.019 5βwft

(1c)

(1d)

式中，α1为黏结-滑移曲线下降段参数；βw为宽度影响系数；ft为混凝土轴心抗拉强度，MPa.

参考文献[10-13]的研究，本文采用幂法准则作为复合受力模式下FRP片材-混凝土界面的起始损伤与失效准则，用来描述界面损伤演化及界面剥离的发生与扩展，即

(2a)

(2b)

式中，GⅠ和GⅡ分别为复合受力模式下的界面Ⅰ型和Ⅱ型能量释放率，N/mm；α为幂法准则幂指数.文献[12-13]中幂指数取2.0，文献[11]中取1.0，表明该参数取值目前还不统一，下文将对其进行参数分析.本文数值模拟中暂取α=2.0.

1.3 试验验证

为了验证有限元模型的准确性，采用文献[7]中的试验结果对本文数值模拟进行验证.数值模拟与试验的荷载-位移曲线如图4所示，可看出数值模拟结果与试验值总体上较为接近，能够反映复合受力模式下FRP片材-混凝土界面的整体受力特性，本文将根据此模型对复合受力模式下FRP片材-混凝土界面受力的主要影响因素进行参数分析.

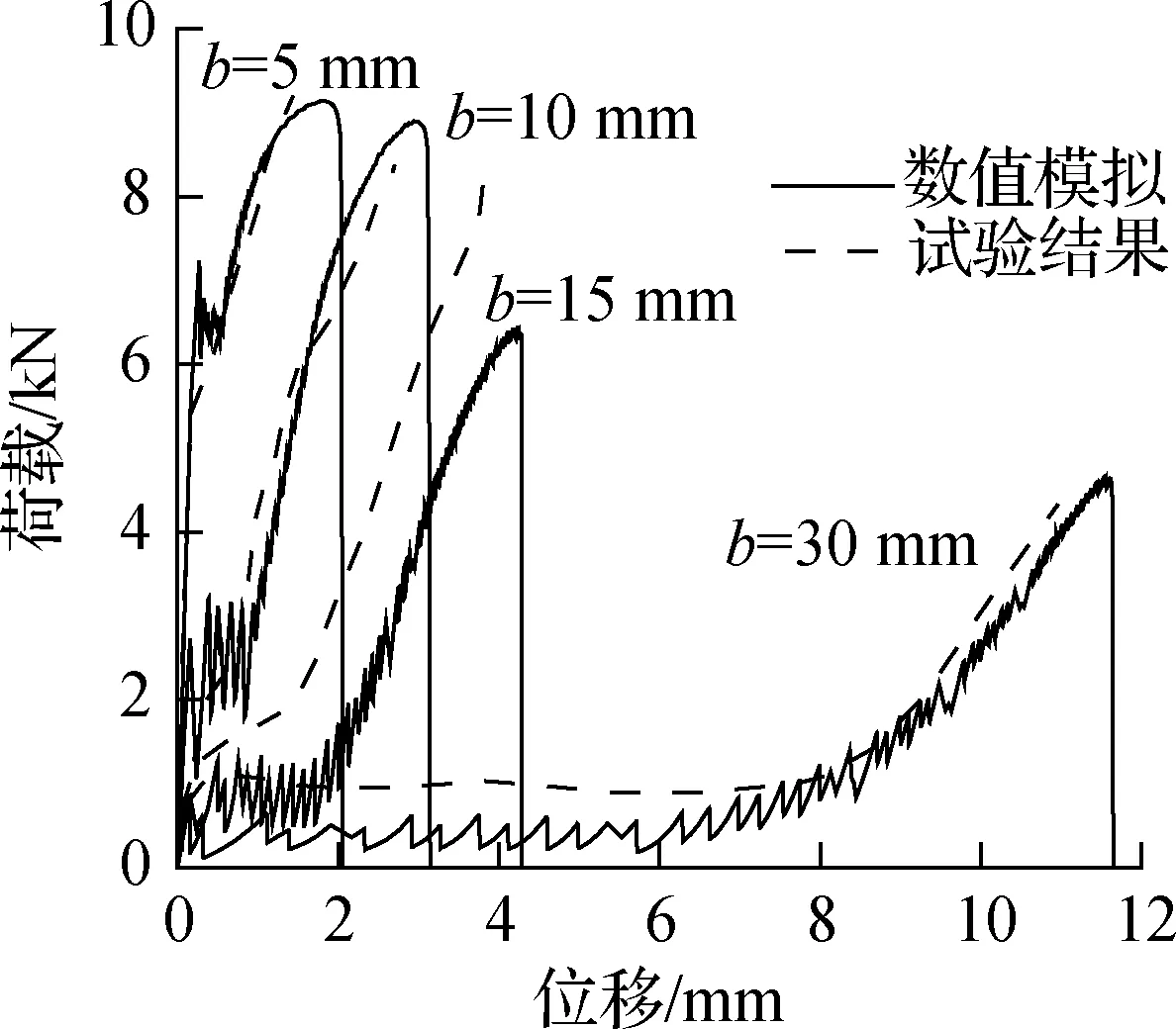
图4 数值模拟与试验结果对比

2 复合受力模式下的界面影响因素分析

基于既有研究，对复合受力模式下FRP片材-混凝土界面性能可能有影响的参数包括：幂法准则幂指数α、混凝土强度、FRP刚度Eftf与黏结长度L、黏结-滑移参数(EⅠ、EⅡ、GfⅠ、GfⅡ、σmax、τmax)等.本节以4组不同加载角下双剪试件的数值模型为基准，对这些影响因素进行参数分析，其中混凝土强度对界面性能的影响主要体现在黏结-滑移参数中，所以不再进行讨论.

2.1 幂法准则幂指数的影响

以幂法准则幂指数α为变量进行参数分析，对不同初始加载角下的界面荷载-位移结果进行对比，如图5所示.当α=0.5时，对应的荷载-位移曲线峰值相对较小.当幂指数取1.0、1.5、2.0、3.0时，相应的荷载-位移曲线都比较接近，且与试验曲线较为符合.因此，可认为α取值在1～3范围内均能较好地反映试验结果.

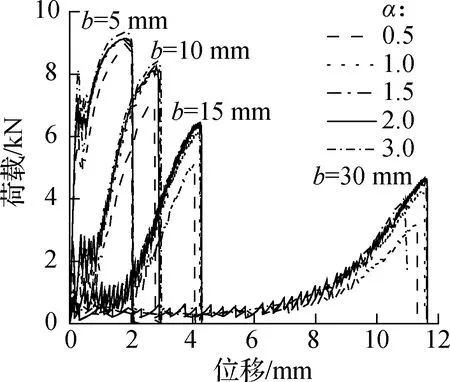
图5 幂法准则幂指数对荷载-位移曲线的影响

2.2 界面黏结刚度的影响

以界面法向黏结刚度EⅠ为变量进行参数分析，得到的荷载-位移曲线如图6(a)所示.对比同加载角模型可知，EⅠ取值越大，初始剥离荷载值越大，极限剥离荷载也越高；对比不同加载角模型可知，加载角较小(界面受Ⅰ型剥离力影响小)时，EⅠ对初始剥离的影响较为明显，对极限剥离荷载的影响很小，而加载角较大(界面Ⅰ型剥离力大)时，EⅠ对初始剥离影响不明显，对极限剥离荷载影响较大.同样地，以界面切向黏结刚度EⅡ为变量，得到的荷载-位移曲线如图6(b)所示.EⅡ取值越小，对应的初始剥离和极限剥离越大，这与EⅠ的影响相反.对比不同加载角模型可知，各加载角下EⅡ对荷载-位移曲线的影响均表现出类似的规律.

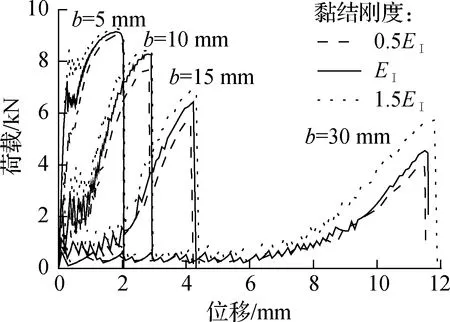
(a) EⅠ的影响(EⅠ=77 MPa)

2.3 界面断裂能的影响

图7给出了界面法向和切向断裂能GfⅠ和GfⅡ对不同初始加载角下界面荷载-位移曲线的影响.如图7(a)所示，GfⅠ取值越大，加载角小的模型中初始剥离荷载明显增大，加载角大的模型中极限荷载明显增大.通过与试验的荷载位移曲线对比，GfⅠ取0.1～0.2 N/mm范围内都能较好地模拟试验.GfⅡ取值越大，初始加载角小的模型初始剥离荷载和极限剥离荷载都明显增大，而加载角大的模型受GfⅡ的变化的影响相对较小.

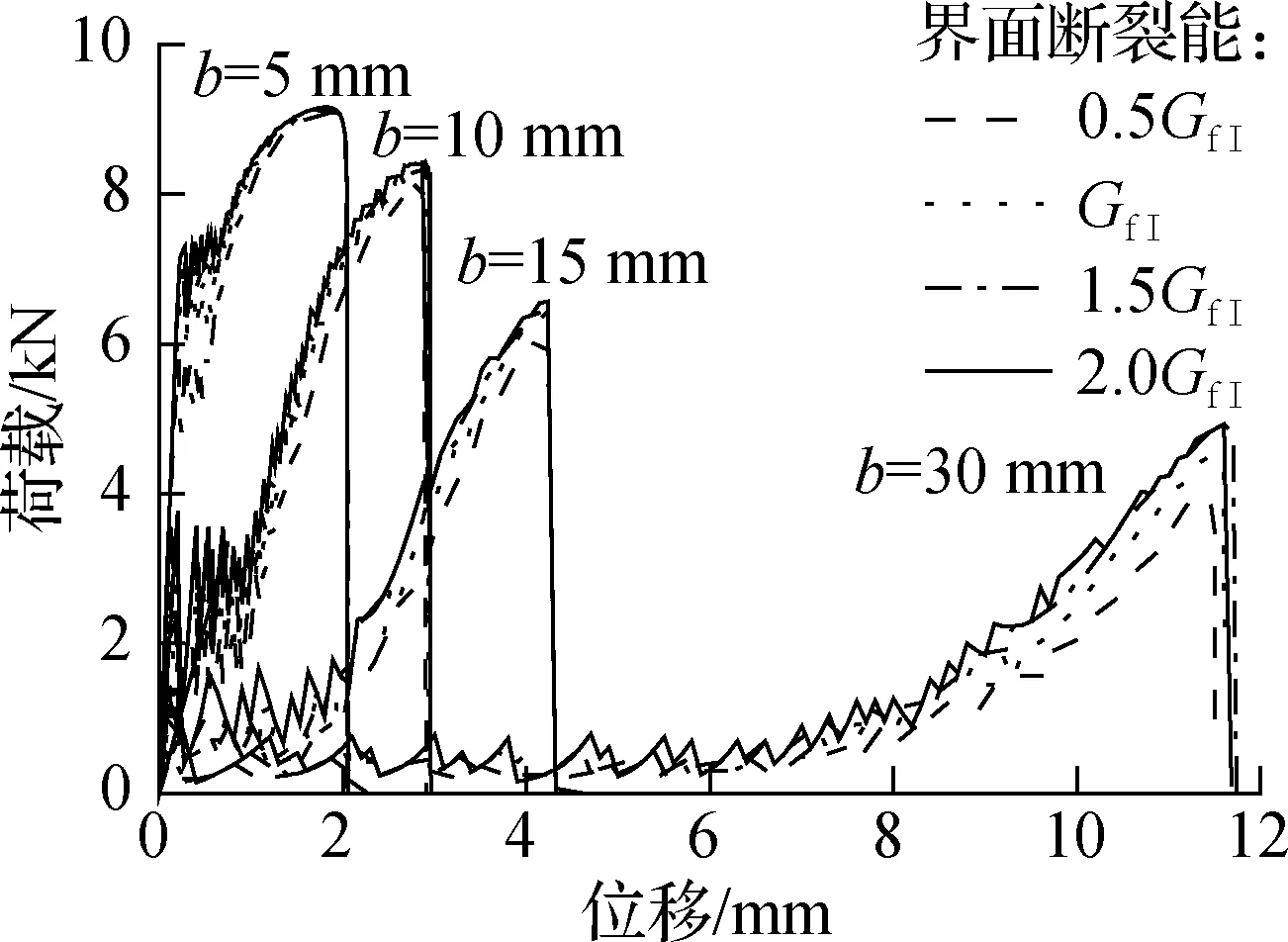
(a) GfⅠ的影响(GfⅠ =0.1 N/mm)

2.4 界面局部黏结强度的影响

图8给出了界面法向和切向局部黏结强度σmax和τmax对不同初始加载角下界面荷载-位移曲线的影响.由图可知，σmax对荷载-位移结果影响不明显，τmax的影响略大于σmax.对比还发现，界面只有在加载角较大时受σmax影响才相对较大，因此整体剥离过程中受剪切的影响较大.

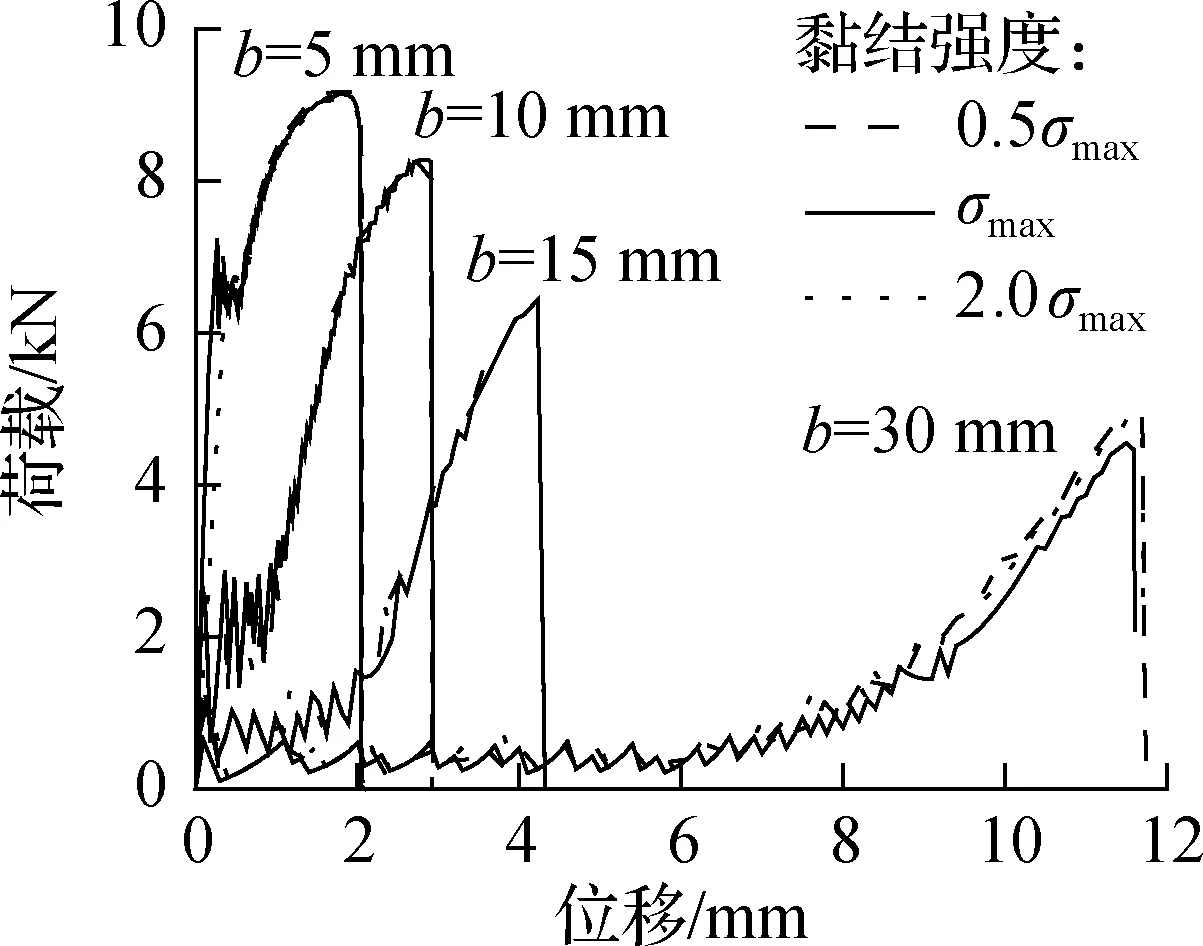
(a) σmax的影响(σmax=2.87 MPa)

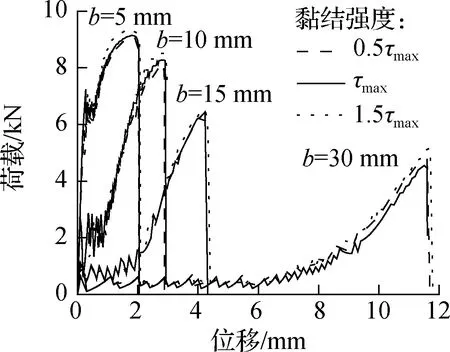
(b) τmax的影响(τmax=4.3 MPa)

2.5 FRP刚度的影响

图9给出了FRP刚度Eftf对不同初始加载角下界面荷载-位移曲线的影响.由图可知，Eftf大小对初始剥离荷载的影响不大，对极限剥离荷载的影响较为明显，Eftf越大，极限剥离荷载越大，而极限位移则越小.这说明采用高弹性模量的FRP材料或者增加粘贴层数都能提升界面承载力，但界面的延性随之变差.此外，随初始加载角的增大，界面承载力的提升幅度逐渐变小，表明在较大的加载角下刚度较大的FRP片材更容易发生界面剥离破坏.

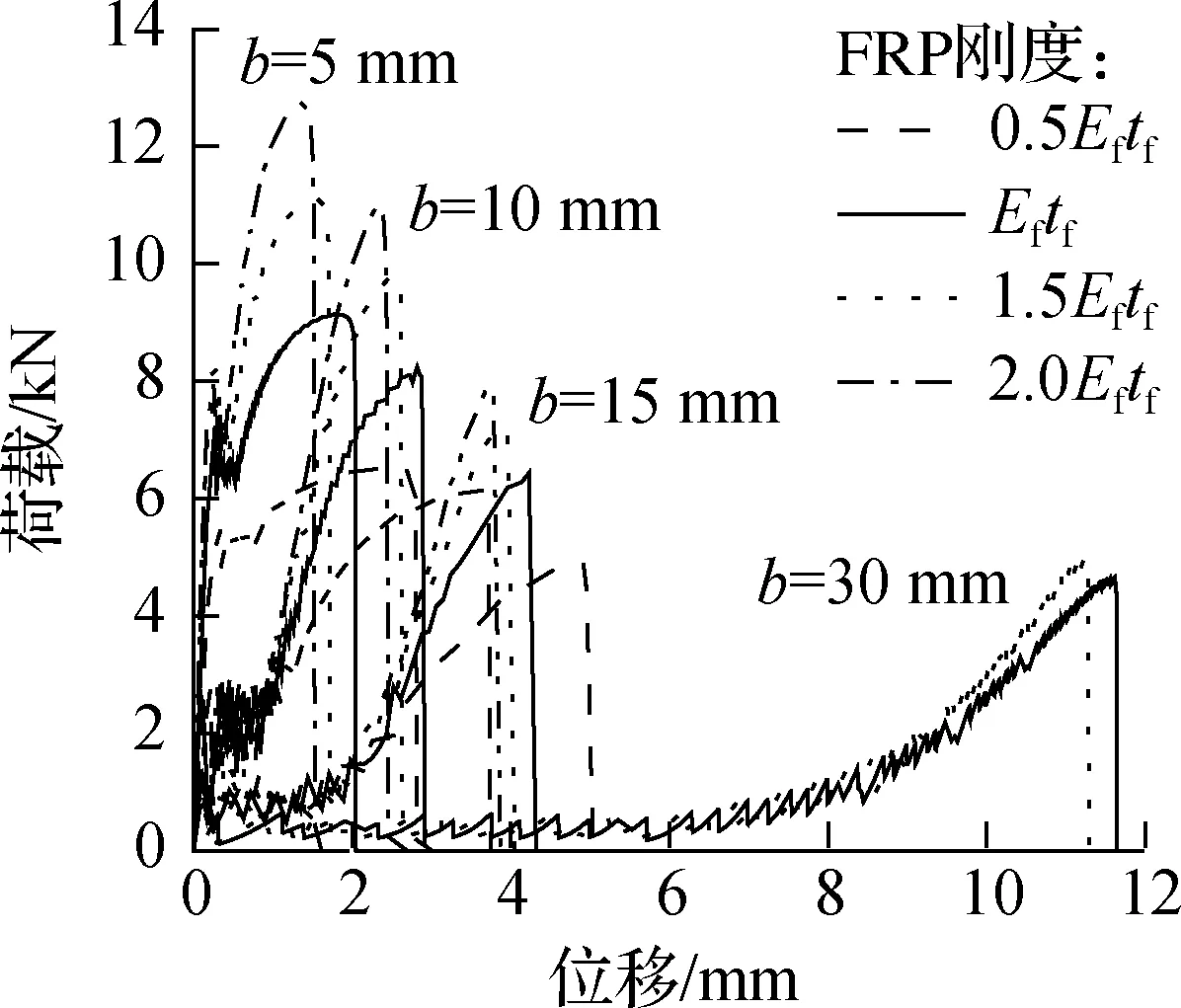
图9 FRP刚度对荷载-位移曲线的影响(Eftf=33 748 N/mm)

2.6 FRP黏结长度的影响

根据既有研究，上述基准双剪试件在纯剪受力模式下的界面有效黏结长度约为100 mm，本参数分析分别设置FRP黏结长度L为50、100、200、300 mm，以分析黏结长度对界面荷载-位移曲线的影响，如图10所示.由图可知，黏结长度仅对极限剥离荷载有影响，黏结段长度越长，极限剥离荷载越大，直至达到纯剪受力模式对应的极限剥离荷载，而对初始剥离荷载几乎没有影响.这主要是由于：① 界面剥离主要受临界剥离时FRP片材加载角的影响，L越长，几何关系上界面达到最终剥离时的加载角就越小，随L的增加，界面极限荷载将逐渐增大并接近纯剪受力状况；②界面初始剥离角是固定的，不受FRP黏结长度的影响，因此界面初始剥离荷载几乎不变.

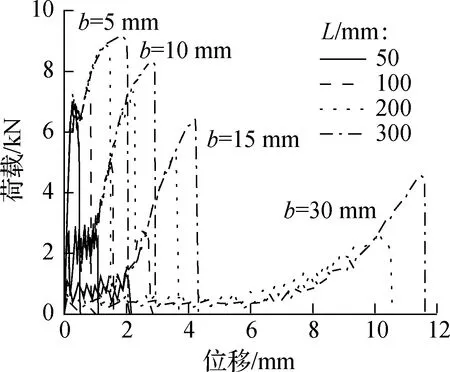
图10 FRP黏结长度对荷载-位移曲线的影响

3 复合受力模式下FRP片材-混凝土界面承载力预测模型

陆新征等[4]依据其建立的界面黏结-滑移模型，进一步推导得到了纯剪受力模式下FRP片材-混凝土界面的承载力预测公式，即

(3)

式中，Pu为纯剪受力模式下的界面剥离承载力，kN.

为了考虑界面复合受力模式的影响，将上述数值模拟所得界面极限承载力PFE与式(3)预测值Pu进行比较，所得结果如图11所示.基于上述参数分析，本文以FRP片材完全剥离时极限加载角的正切值b/(L+a)为主要变量，来综合反映复合受力模式下初始加载角与FRP黏结长度对界面承载力的影响.由图可知：PFE/Pu随b/(L+a)的增加而显著降低，表现出良好的相关性；当加载角为0时，PFE/Pu也接近1.0，表明纯剪受力模式下该模型与数值模拟结果吻合较好，可在此模型基础上进一步修正以反映界面复合受力的影响.本文采用指数函数的形式反映界面承载力随加载角的变化关系(见图11)，在此基础上得到了考虑复合受力影响的FRP片材-混凝土界面承载力修正模型，即

(4)

式中，PM为修正后的复合受力模式下界面剥离承载力，kN.

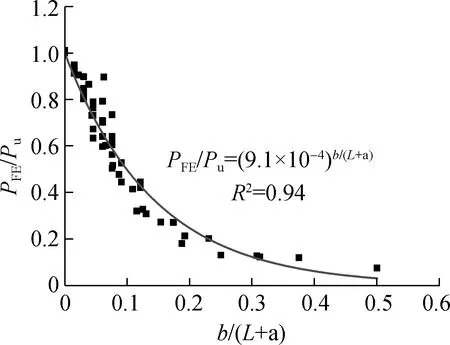
(a) 预测结果及拟合分析

为了验证模型的准确性，根据文献[7-9]中复合受力模式下FRP片材-混凝土界面性能相关的试验数据，并用式(3)、(4)分别计算得到修正前后的界面承载力预测值Pu和PM，如表2所示.其中，Pexp为界面剥离承载力试验值.图12给出了模型修正前后界面极限荷载预测值与试验值比值的分布情况，该数值越接近1.0说明预测效果越好.由图可知，相比原始模型，修正模型的平均值更接近于1.0，总体上预测结果偏于安全，离散性更小，变异系数由31.3%降低至17.4%，预测结果与试验值比值的分布范围更加集中，预测精度得到显著提高.以上分析表明，本文所提修正模型能够较好地考虑界面复合受力模式的影响，可用于带初始加载角的FRP片材-混凝土界面承载力的预测.

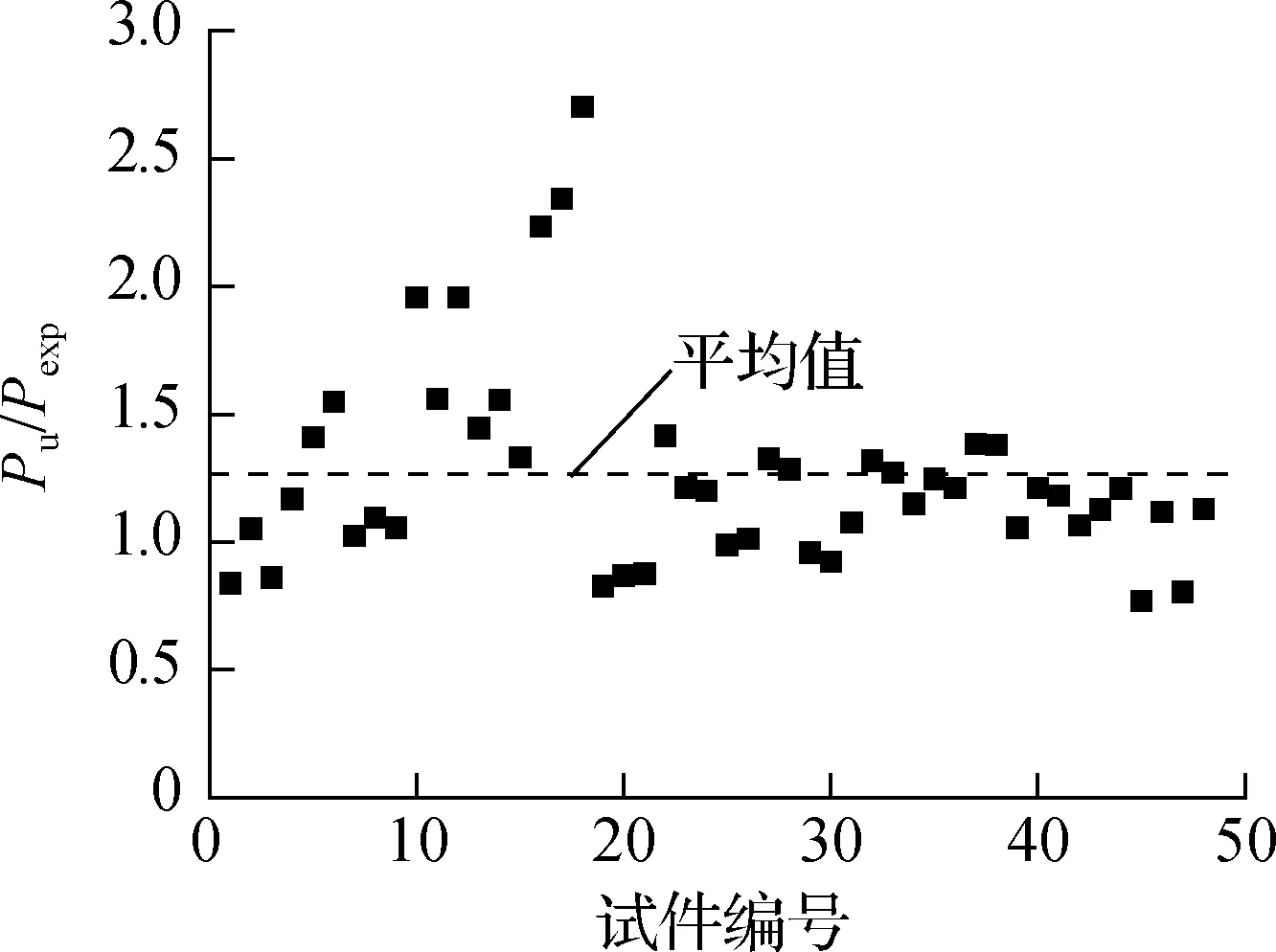
(a) 原始模型

4 结论

1) 基于幂法准则的界面起始损伤与失效准则能够有效反映复合受力模式下FRP片材-混凝土界面的受力行为，在数值建模中建议幂指数取2.0.

2) 初始加载角与FRP黏结长度对复合受力模式下界面性能的影响相对较大，二者决定了极限加载角的大小.初始剥离发生后，加载角随剥离扩展而逐渐变小，界面荷载随之逐渐提高，界面极限承载力与极限加载角密切相关.

3) 以极限加载角为主要参数，对现有FRP片材-混凝土界面承载力模型进行修正，得到能够考虑复合受力模式的界面承载力预测模型，预测结果的变异系数由31.3%降低至17.4%.

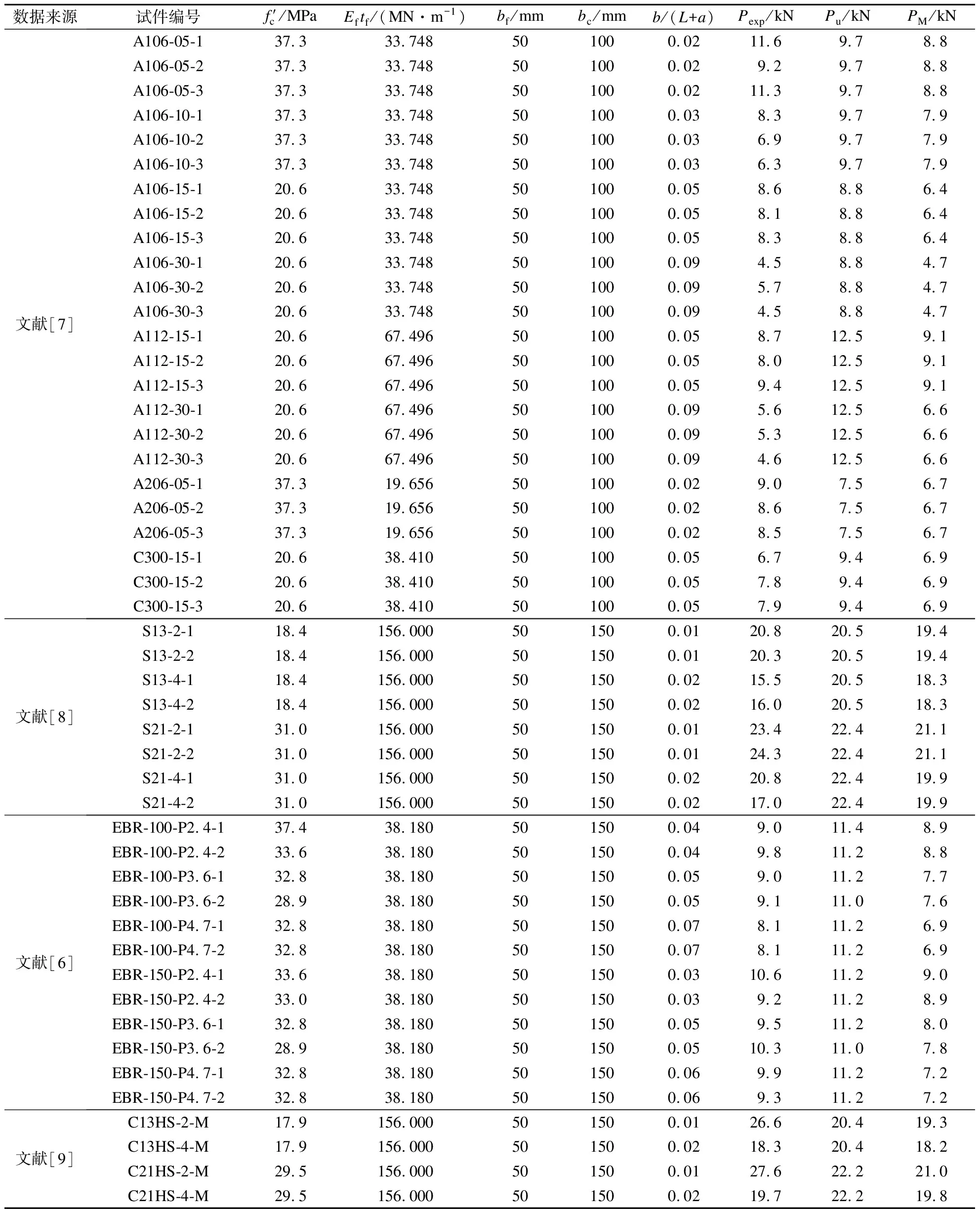
表2 试验数据库及模型预测结果