考虑预应力提高效应的混凝土梁抗剪承载力

李仁强 戚家南 衣忠强 王贤强 程 杭 王景全

(1东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 211189)(2中铁九局集团第一建设有限公司, 苏州 215538)(3东南大学桥梁研究中心, 南京 211189)(4东南大学国家预应力工程技术研究中心, 南京 211189)(5苏交科集团股份有限公司, 南京 211112)

混凝土梁斜截面破坏为脆性破坏,在设计时应保证斜截面具有足够的抗剪承载力,避免发生脆性剪切破坏[1-3].通过对截面施加预应力,可有效提高斜截面抗剪承载力[4-6].预应力混凝土梁受剪机理复杂,影响因素众多,国内外学者开展了大量的试验和理论研究[7-9].车惠民等[10-11]进行了预应力对无箍筋及有箍筋混凝土T形梁抗剪承载力影响的试验研究,发现预应力大小对试验梁混凝土抗剪贡献有提高作用,并给出了预应力混凝土T形梁抗剪承载力计算公式.肖光宏等[12]根据50片有黏结部分预应力混凝土梁和25片无黏结部分预应力混凝土梁的受剪试验结果,对有黏结和无黏结梁抗剪承载力及抗剪机理进行了比较,发现预应力可提高混凝土梁抗剪承载力,且无黏结梁抗剪承载力较有黏结梁低.Cladera等[13]提出了考虑预应力效应的中性轴高度计算方法,基于分项叠加思想,建立了考虑混凝土压杆、开裂腹板、销栓作用和抗剪钢筋的预应力混凝土梁抗剪承载力计算公式.基于混凝土力学原理,通过试验结果和精细化数值分析,Marí等[14]提出了预应力混凝土梁抗剪承载力计算公式,针对ACI-DAfStb数据库样本抗剪承载力的计算结果表明,所提公式可较好地预测预应力混凝土梁抗剪承载力.Nagrodzka-Godycka等[15]搜集了42个预应力混凝土梁抗剪试验数据,比较了Eurocode 2、ACI 318-14和Model Code 2010等规范以及学者们提出的计算方法.然而,关于预应力对混凝土和箍筋抗剪贡献的提高效应研究较少,且缺乏理论量化方法.

本文通过RC梁和PC梁微元体应力分析,剖析预应力对梁抗剪承载力的提升机理.基于桁架模型倾角变化,分析预应力对箍筋抗剪贡献的提高作用;根据承载力提高系数,分析预应力对混凝土抗剪贡献的增强作用,进而推导出PC梁抗剪承载力理论计算公式.基于国内外发生剪切破坏的PC梁试验数据,验证所提公式的准确性并进行参数分析.结果表明,所提公式具有较好的精度且可反映主要因素的影响规律.

1 预应力对RC梁承载力的提高机理

预应力对RC梁承载力的提升主要体现在预应力筋竖向分量的直接抗剪作用以及水平分量的间接抗剪作用2个方面.

图1为RC梁和PC梁隔离体中性轴处微元体应力分析示意图.图中,V为荷载；τ为微元体剪应力；fpc=Apfpcosα/Ac为中性轴处预应力筋对截面产生的预压应力,其中Ap和fp分别为预应力筋面积和有效预应力,α为预应力筋弯起角度,Ac为混凝土全截面面积；τcr为梁体开裂剪应力；ft为混凝土轴心抗拉强度；fd为微元体主压应力；β为主压应力与中性轴的夹角.通过摩尔应力圆可求得RC梁和PC梁开裂应力τcr,RC和τcr,PC分别为

τcr,RC=ft

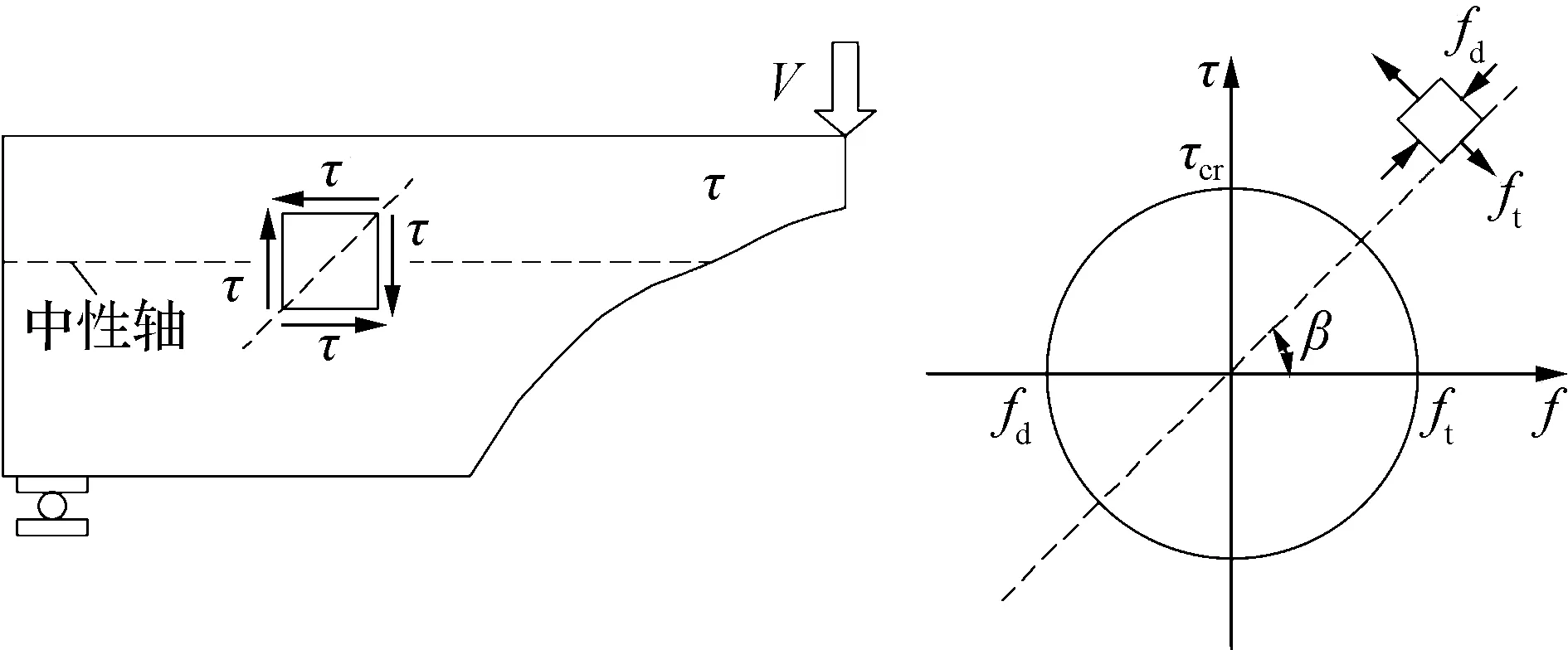
(a) RC梁

预应力筋水平分量使中性轴处微元体应力状态发生改变,减小混凝土主拉应力,延缓裂缝出现并抑制其发展,显著提高RC梁开裂荷载及裂后性能.此外,预应力可增加剪压区高度,提高混凝土抗剪贡献.

桁架模型被广泛用于箍筋抗剪贡献计算中.图2为预应力对箍筋抗剪贡献提高机理分析示意图.图中,θRC和θPC分别为桁架模型中RC梁和PC梁的倾角.对于RC梁,现行规范及多数抗剪理论采用45°桁架模型.对于PC梁,由于预应力筋水平分量的轴向预压作用,剪压区内梁体主拉应力倾角变大,斜裂缝倾角变小,能跨过更多箍筋,从而提高箍筋抗剪贡献.

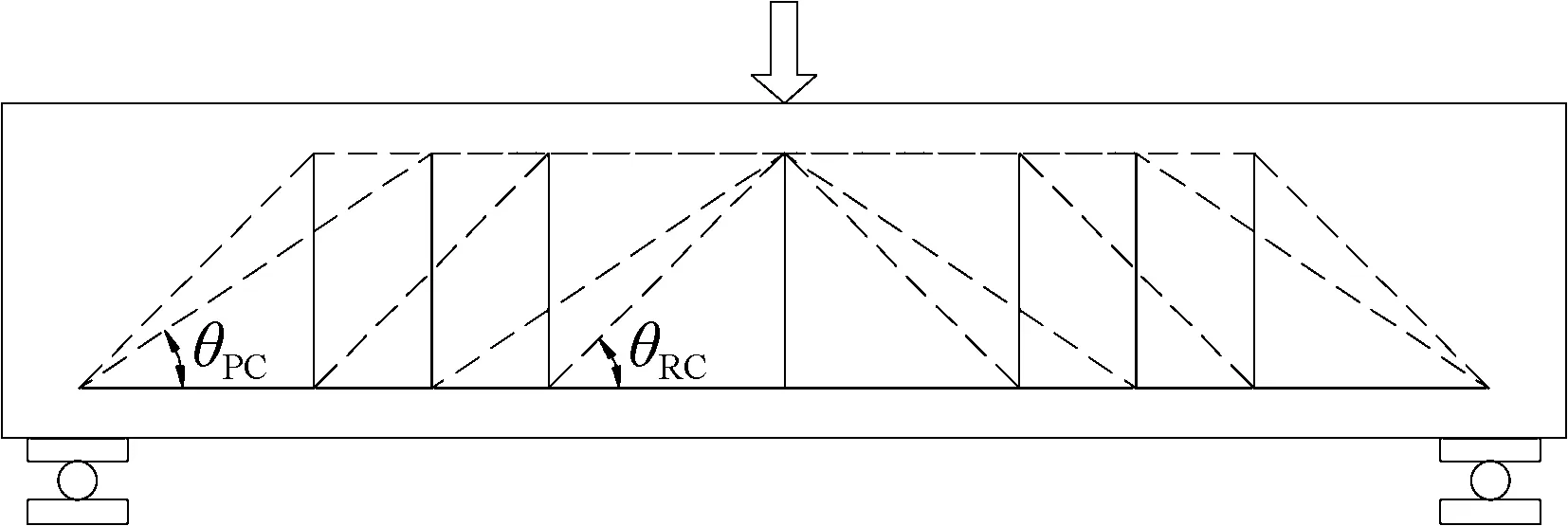
图2 预应力对箍筋抗剪贡献提高机理分析示意图

2 预应力混凝土梁抗剪承载力

2.1 预应力弯起筋抗剪贡献

对于布置弯起筋的PC梁,预应力筋竖向分量直接提供抗力,其计算公式为

Vp=Apfpsinα

(1)

2.2 考虑预应力提高效应的箍筋抗剪贡献

箍筋抗剪贡献可由桁架模型确定(见图3),其计算公式为

(2)

式中,d为梁截面有效高度；θ为桁架模型倾角；s为箍筋间距；Av为箍筋面积；fv为箍筋应力,一般取屈服强度fyv；b为梁宽.

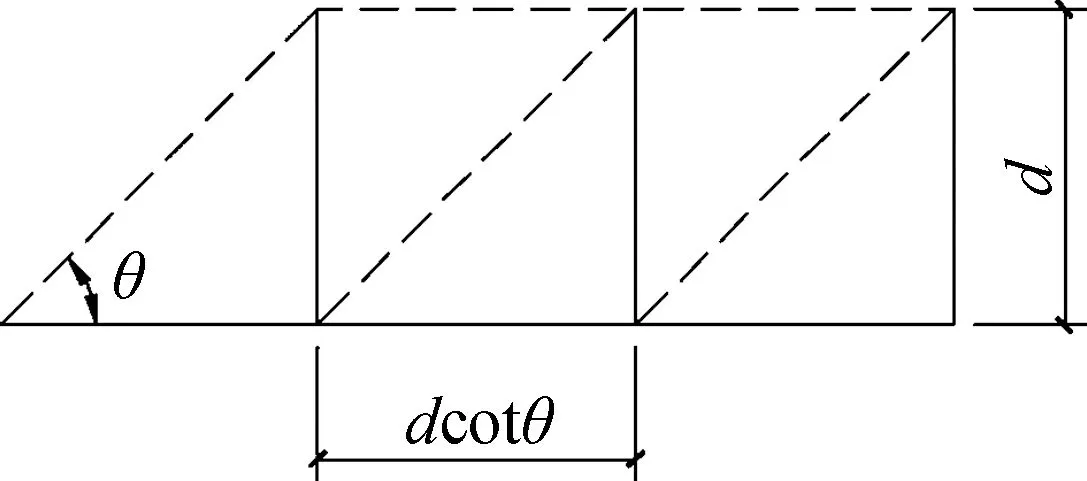
图3 桁架模型

根据文献[16-17],桁架模型的倾角介于25°与45°之间,计算公式为

(3)

式中,N为预应力筋作用在梁上的轴向压力.

Eurocode规范建议混凝土轴心抗拉强度为[18]

(4)

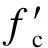
将式(4)代入式(3)可得

(5)

(6)

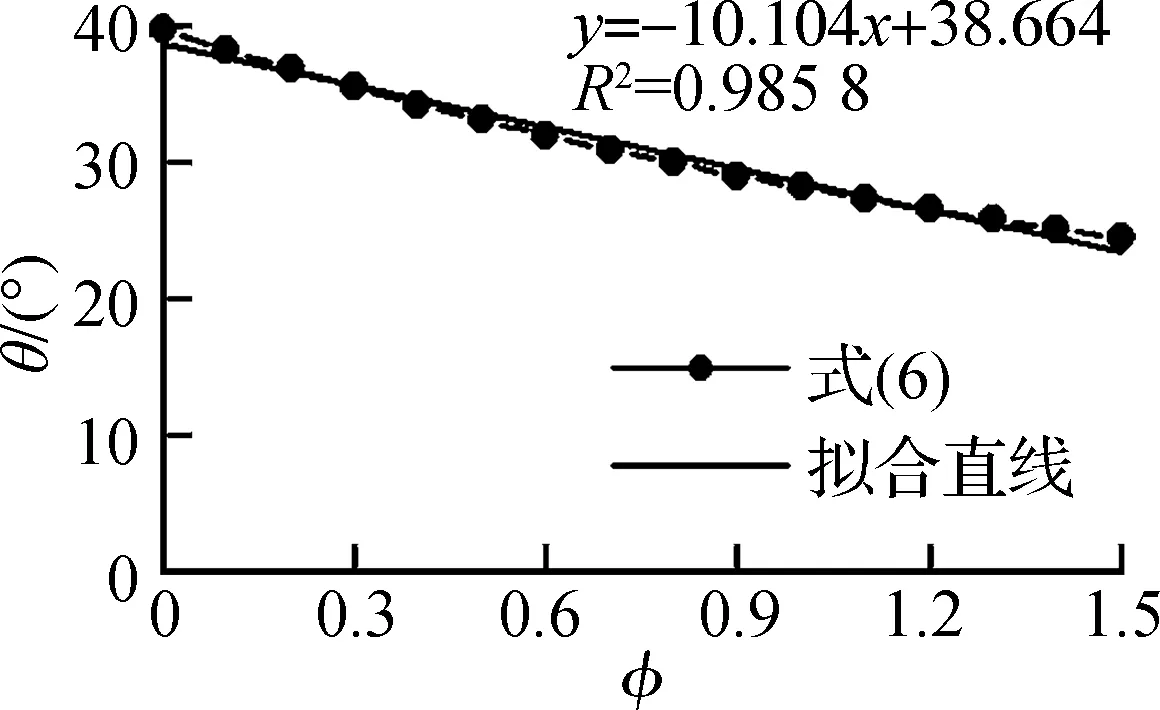
图4 桁架模型倾角的线性拟合图

2.3 考虑预应力提高效应的混凝土抗剪贡献

对于普通混凝土梁,混凝土抗剪贡献可由下式计算[19]：

(7)

(a) 预应力特征值

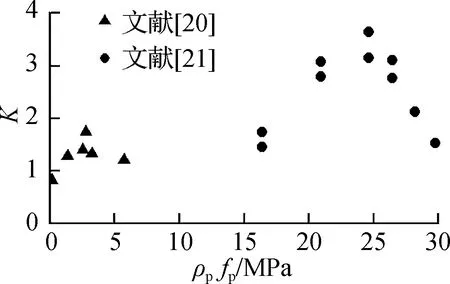
根据文献[26]中414片PC试验梁的提高系数K,以相关系数最大为目标,拟合出最优曲线,结果见图6.为计算简便,建议K取值为

(8)

图6 提高系数回归分析

2.4 考虑预应力提高效应的混凝土梁抗剪承载力

预应力混凝土梁抗剪承载力为混凝土抗剪贡献、箍筋抗剪贡献和预应力抗剪贡献的叠加,即

(9)

3 试验验证与讨论

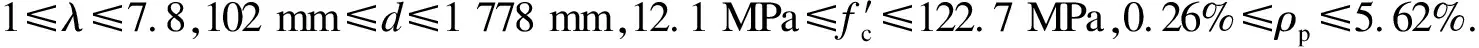
图7给出了PC梁抗剪承载力试验结果与式(9)计算结果比较.由图可知,试验值与计算值比值Δ的均值为1.016,标准差为0.193.由此说明,基于本文建议公式得到的PC梁抗剪承载力预测值与试验值吻合较好,且该公式对不同参数变化情况下的预测结果较为稳定.

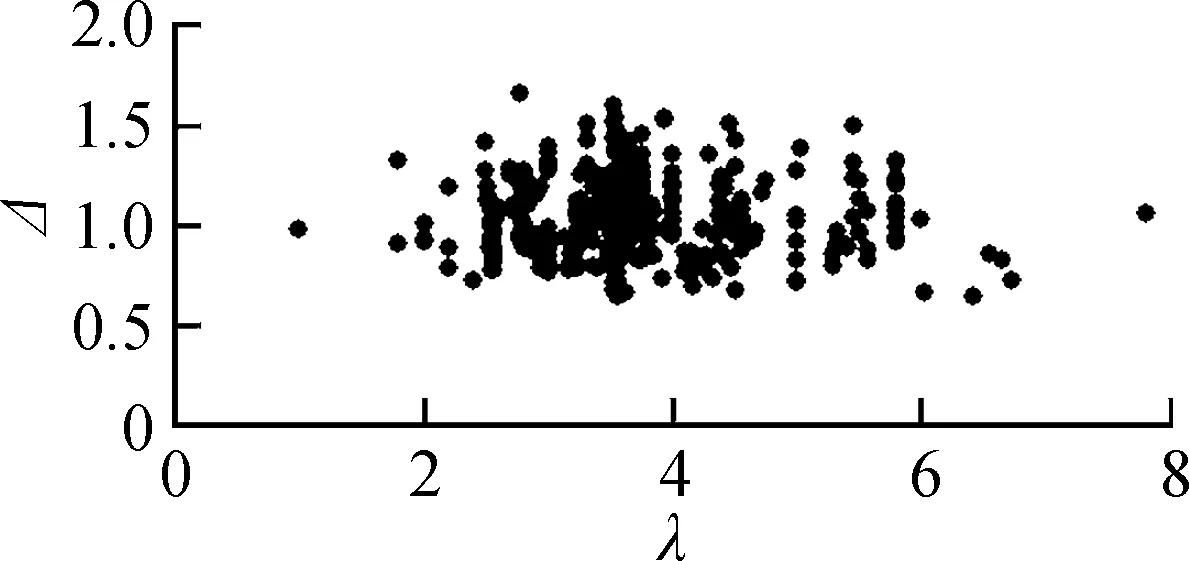
(a) 剪跨比

以文献[21]中1E梁为基准试件,对本文建议公式进行参数分析,结果见图8.由图可知,PC梁的抗剪承载力随剪跨比增加而降低,并趋于稳定.剪跨比较小时,抗剪承载力下降较快；剪跨比较大时,抗剪承载力下降趋势减缓.抗剪承载力随预应力筋配筋率的提高而增加；当预应力筋配筋率较大时,抗剪承载力趋于定值.随着预应力筋弯起角度的增加,抗剪承载力近似线性增加,说明预应力筋竖向分量直接抗剪作用较水平分量的间接抗剪作用更为显著.

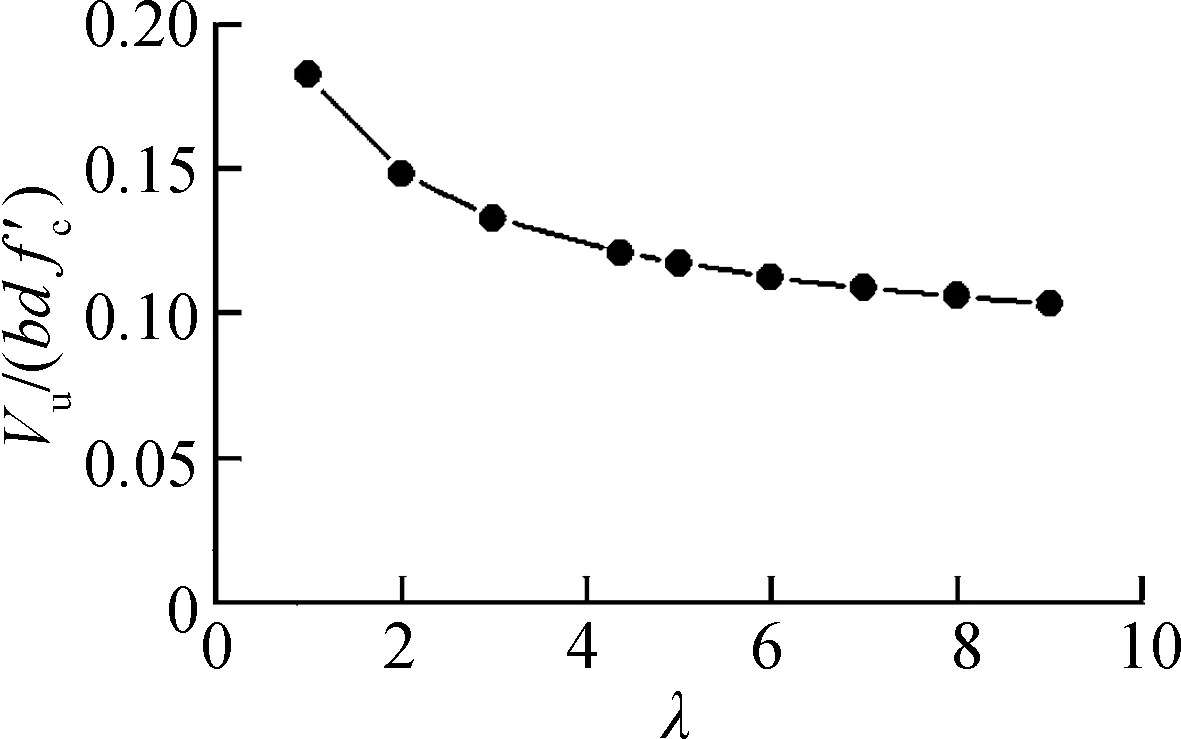
(a) 剪跨比

4 结论

1) 考虑预应力、剪跨比和混凝土强度等参数影响,提出了预应力对混凝土抗剪贡献提高系数计算方法.通过桁架模型倾角变化,考虑预应力对箍筋抗剪贡献的提高效应,叠加预应力竖向直接抗剪贡献,得到预应力混凝土梁抗剪承载力的理论计算公式.

2) 基于所提公式得到的抗剪承载力预测值与414片预应力混凝土梁抗剪承载力试验值吻合较好.抗剪承载力试验值与计算值的比值均值为1.016,标准差为0.193.

3) 所提公式可综合考虑梁体几何尺寸、混凝土强度、剪跨比、预应力、配箍率等主要影响因素,适用范围较广,形式简单,便于推广应用.