非金属原子掺杂的GaN 纳米管:电子结构、输运特性及电场调控效应*
汤家鑫 范志强 邓小清 张振华
(长沙理工大学,柔性电子材料基因工程湖南省重点实验室,长沙 410114)
1 引言
石墨烯的成功制备使二维(2D)材料的研究走进人们的视野[1-2],其独特的结构和优良的性质受到极大关注,目前已有大量2D 材料被制备,其电子相覆盖绝缘体、半导体及金属.然而,这些材料在实际应用方面也存在不足,例如石墨烯,虽然其具有优异的物理及化学性质,特别是载流子迁移率可达2 × 105cm2/(V·s)[3,4],但其零带隙半金属性质极大地限制了在场效应管(FETs)方面的应用[5].而黑磷具有依赖层数的0.3—2.0 eV 的直接带隙[6]和103cm2/(V·s)的高空穴迁移率[7,8],但其自身稳定性差,在空气中极易氧化.近年来热门的单层MoS2,虽具有1.8 eV 的直接带隙,但其载流子迁移率仅有102数量级[9],导致在场效应管方面的应用也受到限制.因此,不断探索新的高性能2D 材料是非常必要的,近年来,越来越多的2D 材料被陆续发现,其中有很多具有优良性质的单层材料[10,11],如GaN.
众所周知,GaN 具有高电子迁移率和热导率,被称作第三代半导体,一直备受科研人员的关注[12],其衍生出的低维材料也成为研究热门,例如最近的研究发现,二维GaN 具有1.68 eV 的间接带隙,并且容易制备,其结构为类似石墨烯的蜂窝状平面材料[13-16].将二维GaN 进行裁剪形成的一维GaN纳米带也被广泛研究[17,18].为了得到合适的电子性质,人们尝试使用各种手段对GaN 进行调控,例如吸附、掺杂、缺陷等[19-21].源于制备碳纳米管的灵感,人们也尝试制造GaN 相关一维纳米管,以Al2O3或六方ZnO 纳米线为衬底,利用气相外延低温生长的方法,科研人员成功制备了GaN 纳米管[22,23].据报道,GaN 纳米管表现为半导体,但是不同边缘结构的纳米管会表现出不同的电子性质,扶手椅边缘纳米管表现为间接带隙,锯齿边缘纳米管表现为直接带隙,其次随着纳米管直径的增大,带隙也增大,另外锯齿边缘比扶手椅边缘更稳定[24-26].
掺杂是调控材料电子性能的一种有效手段,被广泛应用于研究,其中对纳米管进行掺杂是一个热门方向,已有不少研究[27-29].对于GaN 纳米管[24-26],引入不同的掺杂原子,不但可以有效地调节带隙,还能提高材料的光学性质,使功能化的GaN 纳米管在电子及光电子器件方面更具应用价值.但是目前对GaN 纳米管掺杂研究,往往停留在考虑掺杂几种特定的原子上,由于掺杂原子的种类过少,很难发现掺杂导致的电子性质的变化规律,现有研究文献没有通过掺杂不同原子来研究其电子相变化规律.
本文利用密度泛函理论,对GaN 锯齿纳米管进行掺杂研究,考虑了从第ⅢA 族到第ⅦA 族的所有非金属原子低浓度掺杂情况,计算发现:结合能、形成能及杂质原子周围化学键的平均键长与掺杂原子的原子序数(原子半径)密切相关,而杂质原子与纳米管间的电荷转移与它们之间的相对电负性有直接关系.特别是,纳米管的电子相随不同原子掺杂表现出很强的规律性,掺杂第IIIA,VA,VIIA 族原子后,纳米管仍为半导体,而掺杂第IVA,VIA 族原子后,纳米管变为金属,即掺杂纳米管电子相有明显的奇-偶效应.同时发现掺杂异质原子,能调控纳米管的空穴及电子迁移率到1 个数量级的差异,特别是较高的栅极电压能明显提高空穴及电子迁移率.总之,本文获得到结果及讨论的调控方法对于材料及相关器件设计能提供有价值的参考.
2 计算方法
模型的几何优化、结构稳定性的评估、电子和输运特性的计算都采用基于密度泛函理论(DFT)的第一性原理方法.所有这些计算都是在Atomistix ToolKit(ATK)软件包中实现,这种方法已被广泛应用于研究纳米结构[30-36].在计算中,选择广义梯度近似的Perdew-Burke-Ernzerhof (PBE)形式作为交换关联势.用Troullier-Martin 模守恒赝势来表示原子核和原子轨道的线性组合,基函数组选用DZP (Double ζ+Polarization).k点采样在x,y和z方向上分别为1,1 和100.本文中z方向是管轴方向,也定义为传输方向,且采用周期性边界条件.为了追求计算效率与精度平衡,能量截断半径设定为150 Ry,用以控制实空间积分网格区间的尺寸以及泊松方程的求解.在所有研究的模型中,在x和y方向设置了一个超过20 Å (1 Å=0.1 nm)的真空层,用以消除管与“管像”之间的相互作用.结构优化标准是作用在每个原子上的力小于0.01 eV/Å,晶格内应力小于0.01 GPa.所有的计算都在几何结构优化之后进行,能量收敛标准为10—5.为了简单起见,在所有计算结果中,系统的费米能级设置为零.
3 计算结果与分析
3.1 化学结合及稳定性
单层GaN 是类似于石墨烯的六元环结构,在每个六元环中,N 原子和Ga 原子交替分布,彼此成键,进行几何优化后结构的晶格常数和Ga—N键长分别为3.236 Å和1.87 Å,这与之前DFT 研究的3.260 Å和1.880 Å非常一致[37],将单层GaN进行裁剪可以得到不同边缘结构的纳米带,图1(a)所示为GaN 纳米带的模型图,并分别给出了GaN纳米带正视图和侧视图,可以看出这是一条宽度为20 个二聚原子链组成的扶手椅型纳米带,虚线框内为纳米带单胞,每个单胞内含有20 个Ga 原子和20 个N 原子,图中a1表示扶手椅方向上的单胞基矢,a2表示锯齿方向上的单胞基矢,前文提到,对于GaN 纳米管,锯齿边缘会比扶手椅边缘更加稳定,因此将GaN 纳米带沿a1方向以水平线为轴卷曲,得到单原子层厚度的锯齿型GaN 纳米管,即本文研究的本征GaN 管,如图1(b)所示,图中给出了该纳米管的正视图和侧视图,其中虚线框为纳米管单胞,分别包含20 个Ga 原子和20 个N 原子,管半径为10.6 Å.同时,在图1(c)中给出了本征GaN 纳米管的能带图,可以看出,它是直接带隙半导体,带隙为2.18 eV.一般来说,本征材料的适用范围十分有限,为了产生新颖物理特性及扩展它的应用范围,考虑替代性掺杂,因为纳米管具有高度的旋转对称性,因此在掺杂时无需考虑被替换原子的位置,只需考虑被替换原子的种类.在本工作中,选取元素周期表中第ⅢA 到第ⅦA 主族的所有非金属原子替换同为非金属原子的N 原子.如图1(d)所示,采取低浓度掺杂,即一个单胞掺杂一个原子,橙色原子即为杂质原子.放大显示的部分为杂质原子与邻近3 个Ga 原子的成键情况,并用d1,d2及d3分别表示相关键长.对于掺杂后的结构,命名为NT-X,其中X表示掺杂原子.对于本征GaN 纳米管而言,其结构是非常典型的III-V族化合物,当不同的原子替换掉N 原子后,改变了原有的化学成分及成键情形,因此,可以预期非金属原子掺杂将导致纳米管具有不同的电子特性.

图1 (a) GaN 纳米带的正视图和侧视图(虚线框内为纳米带单胞);(b) GaN 纳米管的正视图和侧视图(虚线框内为纳米管单胞);(c) 本征纳米管的能带结构;(d) 掺杂纳米管的原子结构,X 表示掺杂原子,d1,d2,d3 分别表示掺杂原子周围的三根共价键Fig.1.(a) Top and side views of GaN nanoribbon (the black dashed-line box indicates the unit cell of GaN nanoribbon);(b) top and side views of GaN nanotube (the black dashed-line box represents the unit cell of GaN nanotube);(c) band structure of intrinsic nanotube;(d) the atomic structure of doped nanotube,X represents a doped atom,and d1,d2 and d3 are three covalent bonds around a doped atom,respectively.
在讨论杂化纳米管电子性质之前,首先计算其结合能以评估其结构相对分离态原子的能量稳定性,结合能EB定义为

其中,ET为掺杂后单胞的总能量,EGa,EN,EX分别为1 个Ga 原子、N 原子以及掺杂原子X在孤立状态时的能量,nGa,nN分别为掺杂后1 个单胞中Ga 原子和N 原子的数目,n=nGa+nN+1 为掺杂后一个单胞中原子总数.根据定义,若结合能为负值,就意味着分离态原子结合成晶体时,能量降低,形成稳定结构,其绝对值越大,结构越稳定.将计算的结合能列于表1,可以看出,所有掺杂纳米管的结合能均为负值,且位于5.19—5.31 eV/atom之间,所以掺杂形成的杂化纳米管相对分离态原子在能量上是非常稳定性的,即在实验上能实现.此外,也可以看出,掺杂纳米管的结合能比本征管的结合能(5.36 eV/atom,对应表中N 掺杂时的情况)略高,所以杂化纳米管相对本征管的能量稳定性略低,这是完全可以理解的.
同时,也可以将掺杂过程视为化学反应,因此可通过计算化学形成能表征杂化管相对本征管的稳定性,化学形成能EF定义为
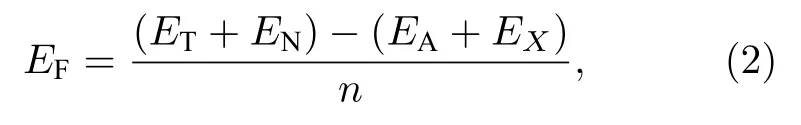
其中EA为掺杂前(本征管) 1 个单胞的总能量.根据该定义,化学形成能表示的是掺杂原子和本征纳米管反应形成掺杂纳米管及替代出N 原子的能量差,若为负值,则意味着化学反应为放热反应,掺杂纳米管在能量上比本征纳米管更稳定;反之为吸热反应,则掺杂纳米管的能量稳定性比本征纳米管低.计算结果列于表1,其中N 原子掺杂表示本征纳米管,可以看出,所有杂化纳米管的形成能均为正值,且位于0.04—0.16 eV/atom 之间,即掺杂纳米管是吸热过程,其能量稳定性降低,与结合能计算结果一致.但是,这些形成能均为较小的值,所以,杂化纳米管在能量上仍是非常稳定的.

表1 掺杂纳米管NT-X 的结合能EB 及化学形成能EF,键长di (i=1,2,3)及平均键长 d¯,电荷转移ΔQ(|e|)(负号表示失去电子),带隙Eg 和电子相EP(金属-M,半导体-S)Table 1.Binding energy EB,formation energy EF,bond length di (i=1,2,3) and averaged bond length d¯,charge transfer ΔQ (|e|) (negative sign indicates a loss of electrons),band gap Eg,electronic phase EP (metal-M,semiconductor-S) for the doped nanotubes NT-X.
事实上,表1 中的结合能和形成能随掺杂元素的变化呈现明显的规律性.对同一主族元素掺杂,原子序数越高,纳米管结合能EB的值负得越少(绝对值越小),形成能EF的正值变大,即杂化管的能量稳定性降低.在图2(a)中,以第IVA 主族非金属元素O,S,Se,Te 吸附为例,可以清楚地看到这一变化规律.这也许是因为在同一主族里,原子半经随原子序数增大而明显增大,即增大的原子半径导致杂质原子与Ga 原子结合减弱,同时,可以看到结合能EB及形成能EF变化有完全一致的变化趋势.而对位于同一周期元素的掺杂,其结合能EB及形成能EF变化较复杂(见表1).以图2(b)中给出第2 周期非金属元素B,C,N,O,F 结合能EB及形成能EF为例.可以看出本征纳米管(图中N 原子的位置)在能量上最稳定,随着掺杂原子在元素周期表上逐渐远离N 原子,其形成能和结合能也随之逐渐增大,其能量稳定性减弱.众所周知,同一周期内,原子半经随原子序数变化较为复杂,即增大核电数使原子核对电子的吸引力增加,导致原子半径变小,同时原子序数增加,也使得外层电子数增加,也可能导致原子半径增大,所以一般在同一周期内,非金属原子半径变化比较复杂.本征管在能量上最稳定,也许是N 原子与Ga 原子半径形成最好的匹配.
为了深入了解掺杂纳米管的几何特征,计算不同掺杂原子X与3 个邻近Ga 原子形成的3 键长d1,d2和d3,如表1 所列.可以看出,与本征纳米管(对应表中N 掺杂时的情况)相比,掺杂后纳米管的键长普遍都拉长,而且键长的变化和掺杂原子半径(与N 原子半径相比较)有很大的关系.如位于同一周期或同一主族的非金属元素,当原子序数较小时,在掺杂后的杂质原子与Ge 原子成的3 个键长几乎一样,当原子序数较大时,这3 个键长几乎都不一致而且和本征材料情况相比相差也较大,最为明显的是卤族(VIIA 族)原子,相对应的纳米管由于掺杂而导致的形变也较大.为了更清楚地体现出掺杂原子周围键长与掺杂元素的关系,引入NT-X的平均键长d¯,定义为:d¯=(d1+d2+d3)/3,相关计算结果也列于表1 中.为具体起见,仍以第IVA 主族非金属元素X(=O,S,Se,Te)及第2 周期非金属元素X(=B,C,N,O,F)为例,分别如图2(c),(d)所示.显然,NT-X的平均键长与其形成能和结合能有着非常相似的变化规律,即同一主族非金属元素掺杂,原子序数越高,平均键长越长,这与杂质原子的半径(如前所述)有明确的对应关系;同一周期非金属元素,在周期表中的位置离N 原子越远,掺杂后平均键长越长,这是因为本征纳米管最稳定,其共价键自然是最短的.
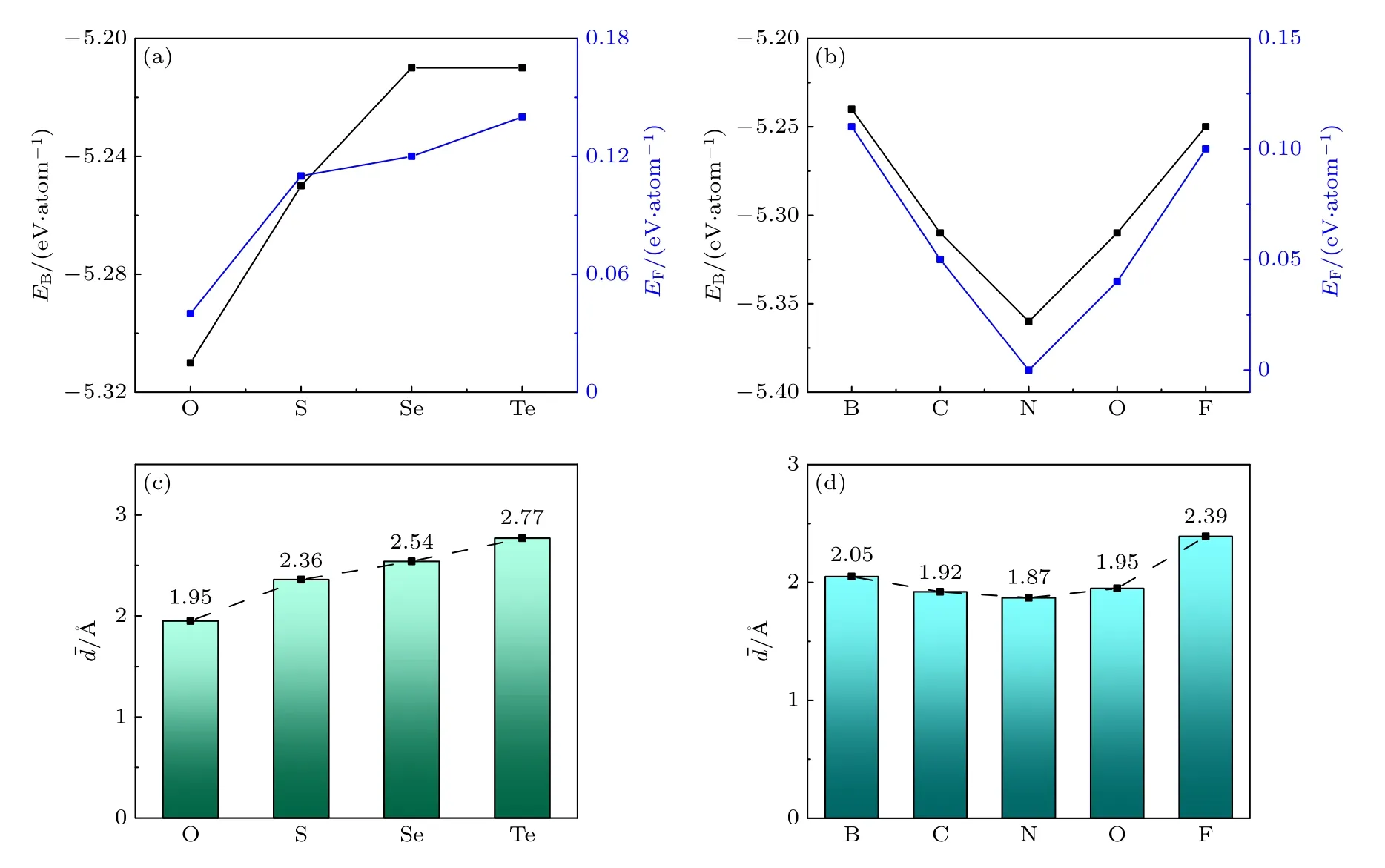
图2 (a) 纳米管NT-X 结合能EB 及形成能EF 随主族VIA 非金属掺杂元素X (=O,S,Se,Te)的变化;(b) 纳米管NT-X 结合能EB 及形成能EF 随第二周期非金属掺杂元素X (=B,C,N,O,F)的变化;(c) NT-X 的平均键长 d¯ 随主族VIA 非金属掺杂元素X (=O,S,Se,Te)的变化;(d) NT-X 的平均键长 d¯ 随第二周期非金属掺杂元素X (=B,C,N,O,F)的变化Fig.2.(a) Formation energy and binding energy versus doped non-metal elements in group VIA for NT-X (X=O,S,Se,Te);(b) formation energy and binding energy versus doped non-metal elements in second period for NT-X (=B,C,N,O,F);(c) averaged bond length d¯ versus doped non-metal elements in group VIA for NT-X (X=O,S,Se,Te);(d) average bond lengthd¯versus doped non-metal elements in second period for NT-X (=B,C,N,O,F).
为了更进一步说明杂化管的稳定存在,评估其热稳定性,即对几何优化后的杂化管进行了Forcite 淬火分子动力学模拟.考虑4 个淬火循环过程,每个淬火循环初始温度和中点最高温度分别设置为300 K 和500 K,即升温到500 K 后再淬火到室温,温度间隔取10 K,总模拟时间为8 ps.图3(b)呈现B,C,P,O,F 掺杂的纳米管淬火后的几何结构,可以看出,与结构优化后的情况相比(图3(a)),淬火处理导致杂化管发生了一定的形变,特别是杂质原子发生了不同程度向内或向外位移,同时也带动邻近的原子移动,但所有管的完整性仍较好保持,没有出现原子间的重构现象,这些说明掺杂后的纳米管具有良好的热稳定性.
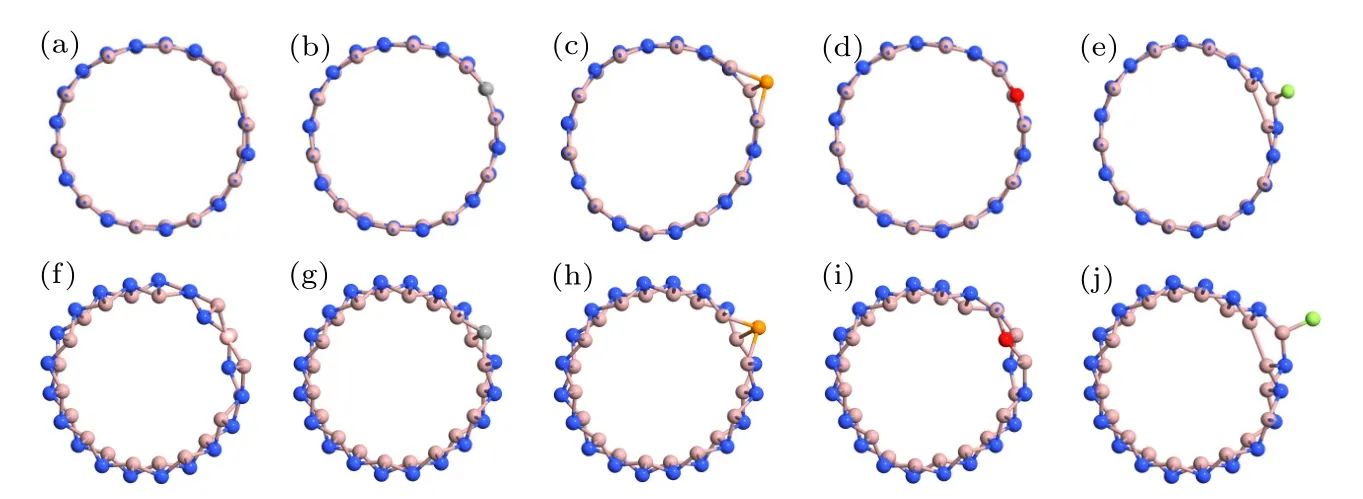
图3 (a)—(e) B,C,P,O,F 掺杂纳米管优化后的几何结构;(f)—(j) B,C,P,O,F 掺杂纳米管淬火后的几何结构Fig.3.(a)—(e) Optimized geometry of B,C,P,O and F doped nanotubes;(f)—(j) geometry of B,C,P,O and F doped nanotubes after annealing simulations.
3.2 纳米管电子结构
为讨论杂化纳米管的电子性质,首先计算所有掺杂原子的电荷转移情况,数据列于表1.为了更清楚地展示这一规律,选取了同一主族和的同一周期元素作为代表,如图4(a),(b)所示.图4(a)给出第IVA 主族非金属元素O,S,Se,Te 四种原子掺杂纳米管后掺杂原子的电荷转移情况,从图4(a)可以看出,随着几种掺杂元素的原子序数的增大,其得到的电荷(电子)越来越少,NT-Te 中的Te原子甚至失去了电荷.这是可以从掺杂元素与邻近相连的元素Ga 的相对电负性得到解释.O,S 和Se 原子的电负性分别是3.44,2.58 及2.55,Ga 原子的电负性是1.81,3 种原子的电负性均比Ga 原子的电负性高,所以O,S 和Se 原子均得到电荷(电子),且随掺杂元素的原子序数的增大而减小.有趣的是Te 元素电负性是2.1,显然高于Ga 元素的电负性(1.81),但Te 原子掺杂纳米管后,恰恰失去电子,如何解释这一现象? 这是因为在2D GaN 材料中,Ga 与N 是结合为分子状态的,即2D GaN 材料是由GaN 分子有序组合而成的,事实上,掺杂原子X是与分子态GaN 相结合的.由于N 元素具有较高的电负性(3.04),使得GaN 分子的整体电负性高于Te 元素,导致Te 元素失去电荷(电子).对于Si 及As 失去电荷(电子)(见表1)可做同样解释.图4(a)给出第二主族非金属元素B,C,N,O,F 掺杂的电荷转移情况,其中N 原子掺杂对应本征纳米管,显然,所有掺杂原子均得到电荷,除了F 原子以外,其他掺杂原子得电荷的数量均随着原子序数的增大而增大.这是因为它们的电负性均高于Ga 元素(1.81),且B,C,N 及O 元素电负性满足2.04(B) < 2.55(C) < 3.04(N) < 3.44(O).然而,F 元素有最高的3.98,但获得的电荷却小于C,N 及O 元素,这是因为NT-F 中F 原子与Ga原子相连的3 个键长di相对于本征纳米管大幅增大(见表1),即形变较大,从而影响了F 原子与Ga原子的电荷转移.

图4 (a) 主族VIA 非金属元素掺杂的纳米管NT-X (X=O,S,Se,Te)的电荷转移;(b) 第二周期非金属元素掺杂的纳米管NTX (X=B,C,N,O,F)的电荷转移.掺杂纳米管的电荷差密度 (c) NT-B;(d) NT-C;(e) NT-P;(f) NT-O;(g) NT-F.青色表示失去电子,洋红色表示得到电子,等值面为0.01e/Å3Fig.4.(a) Charge transfer of group VIA non-metal elements doped NT-X (X=B,C,N,O,F);(b) charge transfer of second period non-metal elements doped NT-X (X=O,S,Se,Te).Charge difference density of doped nanotubes:(c) NT-B;(d) NT-C;(e) NT-P;(f) NT-O;(g) NT-F.Cyan indicates loss of electrons and magenta indicates gain of electrons,and the isosurface is set to 0.01e/Å3.
为了更直观地表示掺杂纳米管的电子分布情况,计算了纳米管的电荷密度差 Δρ,定义为
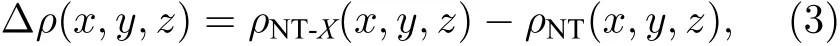
其中ρNT-X为掺杂后纳米管的电荷密度,ρNT为本征纳米管的电荷分布,计算结果如图4 所示,其中青色表示失去电子,洋红色表示得到电子.图4(c)—(e)分别表示B,C 及P 原子掺杂的纳米管,从图中可以看出,掺杂位置相较于掺杂前失去了电子,这是因为B,C 及P 元素的电负性(2.04,2.55,2.12)低于N 元素(3.04),所以相对被取代的N 原子,杂质B,C 及P 原子获得较少的来自Ga 原子的电荷,相当于原N 原子位电荷有“净流出”(青色),而周围的3 个Ga 原子获得电荷(洋红色).而O 原子电负性(3.44)高于N 元素(3.04),所以相对被取代的N 原子,O 原子进一步获得来自Ga 原子的电荷,相当于原N 原子位电荷有少量的“净流入”(洋红色).而对于F 原子虽然电负性高于N 元素,如前所述,F 原子掺杂纳米管形变较大,从而影响了F 原子与Ga 原子的电荷转移,F 原子只能获得较少的来自Ga 原子的电荷,所以,相当于原N 原子位电荷有“净流出”.总之,B,C,P 及F 原子掺杂相当于n 型掺杂,而O 原子掺杂相当于p 型掺杂.这些结果与表1 数据及图4(b)完全一致.
本文重点研究了掺杂纳米管的能带结构(BS)及投影态密度(PDOS),并选取主族的典型非金属原子B,C,P,O 及F 原子的掺杂情况作为代表,相关计算结果如图5(a)—(e)所示,这里的投影态密度是将总态密度(TDOS)投影到N 原子、Ga 原子以及杂质原子上,从而更直观地呈现他们各自对能带的贡献.与此同时,对于不同的掺杂情况,也计算了其特殊子能带的部分电荷密度,即对于掺杂后为半导体的纳米管,计算其最低导带(LCB)和最高价带(HVB)的部分电荷密度,而对于掺杂后为金属的纳米管,计算其穿过费米能级的子能带的部分电荷密度,其相关3D 图列于能带结构(BS)及投影态密度(PDOS)左边(见图5).从图5(a)可以看出,B 掺杂,其纳米管(NT-B)为半导体,但是和本征纳米管不同,NT-B 表现为间接带隙,并且带隙也有明显的减少,即为0.5 eV,其中LCB 和HVB 用蓝色和红色分别表示,从对应的投影态密度可以看出,其LCB 主要由掺杂的B 原子贡献,HVB 主要由N 原子贡献,这一结论可由左边的部分电荷密度分布更直观证实.NTC 的能带结构由图5(b)给出,显然,不同于本征纳米管(图1(c)),NT-C 为金属,从穿过费米能级的子能带(蓝色)的投影态密度可以看出,对该子能带贡献最大的是C 原子,与计算的电荷密度分布完全一样.图5(c)中给出NT-P 的能带结构,明显地,NT-P 的电子性质和本征纳米管十分相近,同样是直接带隙半导体,这也许是因为P 和N 属于同一主族元素,另外从态密度和部分电荷密度分布能看出,P 原子对NT-P 的LCB 和HVB 贡献不大,主要是由Ga 原子和N 原子贡献.图5(d)给出的是NT-O 的能带结构,显然,与C 原子掺杂的情况类似,纳米管为金属,从投影态密度和部分电荷密度分布可以看出,对穿过费米能级的子能带贡献最大的是杂质原子周围的N 原子和Ga 原子,杂质原子O 也有贡献,但较小.最后,NT-F 的能带图见图5(e),NT-F 为间接带隙半导体,从投影态密度及部分电荷密度可以看出,对LCB 贡献最大的是Ga 原子,对HVB 贡献最大的是N 原子.
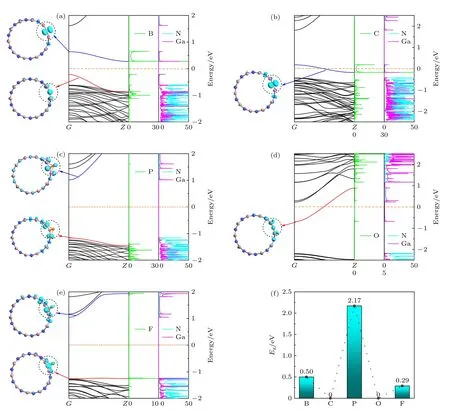
图5 部分NT-X 的能带图以及投影态密度图,左侧为指定子带的部分电荷密度,虚线框内为掺杂原子的位置 (a) NT-B;(b) NT-C;(c) NT-P;(d) NT-O;(e) NT-F;(f) NT-X 的带隙Fig.5.The band structure and projected density of states for part of NT-X,the left panel is the partial charge density for designated subbands,and the position of doped atom is shown in the dotted circle:(a) NT-B;(b) NT-C;(c) NT-P;(d) NT-O;(e) NT-F;(f) the band gap for these NT-X.
从上述分析可以看出,在元素周期表上紧挨着N 原子的C 原子和O 原子掺杂后,纳米管由原来的半导体变为金属,而离其较远的B 原子、F 原子以及同主族的P 掺杂后,纳米管依然为半导体.为清楚起见,总结这几种原子掺杂后纳米管的带隙情况如图5(f)所示,可以看出,相邻主族原子掺杂后纳米管的电子相完全不同,半导体相和金属相交替出现.有趣的是,这是一个普遍规律.可计算获得的5 个主族(IIIA-VIIA)非金属元素掺杂电子相列于表1,其中M 表示金属,而S 表示半导体.显然,同一主族元素掺杂的纳米管其电子相相同,或为半导体或为金属.不同的主族有明显的奇-偶效应,即当吸附的原子最外层电子数目为奇数(掺杂IIIA,VA,VIIA 族的非金属原子)时,纳米管为半导体.而当掺杂的原子最外层电子数目为偶数(吸附IVA,VIA 主族非金属原子)时,纳米管为金属.怎样解释这种有趣的现象呢? 我们知道,GaN 是典型的IIIA-VA 半导体,其中N 原子最外层有5 个电子,Ga 原子最外层有3 个电子,两种原子结合成分子时,会形成最稳定的八隅体结构,在这种结构中,电子是两两成对的,无孤对电子.其他第VA 族的非金属原子最外层同样有5 个电子,当替换N 原子后,并未改变原结构电子排布,因此其掺杂纳米管与本征GaN 纳米管的电子相相同,仍为半导体相.IIIA 及VIIA 主族的非金属原子最外层分别有3,7 个电子,当这些非金属原子掺杂进入纳米管与Ga 原子结合时,也无孤对电子,所以相应的杂化纳米管也为半导体.然而,IVA,VIA 主族的非金属原子掺杂的情况却大不相同,它们的最外层分别有4,6 个电子,与Ga 原子结合时,存在孤对电子.众所周知,孤对电子的能量较高,相应的电子态常处在费米能级附近.由于杂质原子是周期性存在于纳米管里,所以这些孤对电子态形成特殊的子能带.当纳米管为n 型掺杂时,由于纳米管中电子增加以及电子-电子排斥作用使库仑静电势升高,导致孤对电子态形成的子能带向上移动而穿过费米能级,使纳米管成为金属;当纳米管为p 型掺杂时,由于纳米管中电子减少,费米能级下移而与孤对电子态形成的子能带相交,使纳米管成为金属.总之,非金属元素取代纳米管中N 元素的掺杂,电子相有明显的奇-偶性,这一效应与孤对电子态密切相关.另外,从实验的角度来看,纳米管也分为开口、闭口两种,这与制备技术及工艺有关,但在无限长周期性结构理论模型下,边界效应可忽略,即对管来说,无论是管端是可口或闭口的,计算结果相同.
3.3 载流子迁移率
高迁移率半导体材料对于设计场效应管及光电器件有重要应用.利用形变势理论计算半导体性纳米管NT-X(X=B,N,P,As,F,Cl,Br,I)的载流子迁移率,此理论认为影响载流子迁移率的主要机制是长声学波声子散射,其特征量是拉伸弹性模量和变形势常数[38].对于一维半导体系统,载流子迁移率计算公式为[39,40]

其中,e为电子电量,ℏ 为约化普朗克常量,kB为玻尔兹曼常数,T是温度,在计算中取T=300 K,m*表示输运方向载流子的有效质量,E1是载流子的形变势常数,C是弹性模量.根据准自由电子模型,载流子有效质量定义为
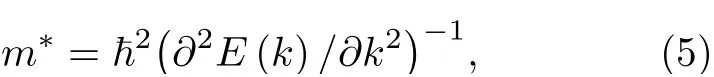
其中,E(k) 为在价带最大(CBM,对应空穴)或导带最小(VBM,对应电子)附近的能量色散关系,k为波矢量.E1和C的定义为
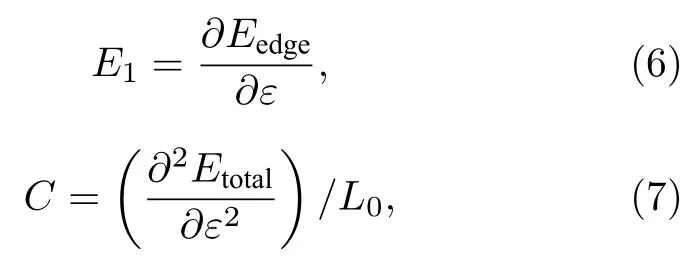
其中,Eedge表示导带底或价带顶的能量,ε表示单轴应变,定义为ε=(L-L0)/L0,其中L和L0分别代表施加外力和未施加外力下沿输运方向的晶格常数.Etotal为单胞的总能量.计算了表1 所列的所有半导体性的掺杂纳米管的有效质量m*、形变势常数E1、弹性模量C及载流子迁移率µ,如图5所示,其中横坐标为相关掺杂原子,为比较起见,还计算了本征纳米管的相关数据,由图中的N表示.首先,由图6(a)可以得出,本征纳米管的电子有效质量较小,为0.223me(me为真空电子的质量),空穴的有效质量相对较大,达到了2.668me,并且通过和其他掺杂纳米管的对比不难发现,除了NT-B 的电子有效质量较大以外,其他掺杂对纳米管的电子有效质量几乎没有影响,这表明即使掺杂导带边附近的能量色散关系也无明显改变.但是空穴的情况就大有相同,随着掺杂原子的改变,纳米管的空穴有效质量变化较大,这表明掺杂能使价带边附近的能量色散关系有明显改变.NT-F 的空穴有效质量最大,达到了4.695me,其他纳米管空穴有效质量比本征纳米管都要小,尤其是NT-B 的空穴有效质量仅有0.353me.
图6(b)给出了空穴和电子的变形势常数|E1|以及弹性模量C,这些都是影响材料载流子迁移率的重要物理量,显然,除NT-F 和NT-Br 外,其他元素掺杂的纳米管的电子形变势常数比本征纳米管都要小.同时可以看出,NT-B 和NT-F 的空穴形变势常数比本征纳米管的高,但其他掺杂纳米管的空穴形变势常数比本征纳米管的都要小.弹性模量C 与掺杂原子有明显地依赖性,除卤族原子掺杂的纳米管以外,其他原子掺杂的纳米管的弹性模量都比本征纳米管要大.通过对以上数据的分析我们不难得出,不论是有效质量、形变势常数还是弹性模量,都对掺杂原子的种类十分敏感,因此将对纳米管的载流子迁移率产生明显影响,从而改变纳米管的输运性质.
利用上述各纳米管的有效质量、形变势常数及弹性模量,我们计算的载流子迁移率如图6(c)所示,显然,对于本征纳米管(NT-N),其电子载流子迁移率约为1.3 × 103cm2/(V·s),空穴迁移率约为4.6 × 10 cm2/(V·s),所以电子的可移动性(mobile)高于空穴.同时可以看出:原子掺杂能明显调控纳米管的载流子迁移率,具有最大电子迁移率的是NT-I,值为1.9 × 103cm2/(V·s),具有最小电子迁移率的是NT-B,值为1.02 × 102cm2/(V·s),最大与最小电子迁移率相差1 个数量级.具有最大空穴迁移率的是NT-B,值为5.5 × 102cm2/(V·s),具有最小空穴迁移率的是NT-F,值为10 cm2/(V·s),最大与最小空穴迁移率也相差1 个数量级.除NTB 外,其他掺杂纳米管的空穴迁移率都较低,明显低于电子迁移率,类似于本征纳米管情况,如NTF,其电子迁移率约为空穴迁移率的72 倍,表现出明显的载流子极性(carrier polarity).载流子迁移率极性现象在光催化的电子和空穴分离方面有着重要的用途.

图6 (a) 半导体性纳米管NT-X (X=B,N,P,As,F,Cl,Br,I)的有效质量m*;(b) NT-X 的变形势常数|E1|和拉伸模量C;(c) NT-X 的载流子迁移率Fig.6.(a) Effective mass m*of semiconducting nanotubes NT-X (X=B,N,P,As,F,Cl,Br,I);(b) deformation potential constant | E1 | and tensile modulus C of NT-X;(c) carrier mobility of NT-X.
3.4 栅极电压调控效应
在图7(a)中,考虑以纳米管为三极管的沟道材料,通过两个栅极对其施加电压,模拟栅极电压对纳米管电子特性,特别是对纳米管迁移率的调控效应.这里选择NT-P 作为代表性纳米管,掺杂原子P 的位置正对上部栅极,且两个栅极的距离设置为3 nm.从上栅极到下栅极的电压定义为栅极电压的正方向,由图中的红色箭头标出,否则称为负方向.当改变栅极电压的大小时,纳米管内的电子会发生横向转移,因此计算了在不同栅极电压下掺杂原子与纳米管的电荷转移,如图7(c)所示.由前文所述(见表1),零电场时NT-P 中P 原子获得的电荷为0.131|e|,很明显,随着电场的正向增加,P 原子得到的电子也随之增加,反之则减少,呈线性变化关系.值得一提的是,当对纳米管施加18 V的反向电压时,P 原子由原来的得电子变成了失电子,可见栅极电压对纳米管内部电荷转移的影响是非常大的.栅极电压导致纳米管内的电荷密度的重新分布,按照密度泛函理论,纳米管的电子特性,如能带结构将发生相应变化,在图7(b)中,画出了NT-P 的CBM 和VBM 随栅极电压的变化曲线,可以看出,不论栅极电压的方向如何,随着电压的增大,NT-P 的带隙变得越来越小,但正、反电压作用下,带隙变化曲线并不完全对称,这正是掺杂效应.

图7 (a) NT-P 外加栅极电压示意图;(b) 不同栅极电压下NT-P 中杂质原子P 的电荷转移;(c) 不同栅极电压下NT-P 的CBM 和VBM 的变化;(d) NT-P 的有效质量m*随栅极电压的变化;(e) NT-P 的变形势常数|E1|和拉伸模量C 随栅极电压的变化;(f) NT-P 的载流子迁移率随栅极电压的变化Fig.7.(a) The schematic of applied gate voltage on NT-P;(b) electron transfer of hero-atom P in NT-P versus different gate voltages;(c) changes of CBM and VBM under different gate voltages on NT-P;(d) the effective mass m*of NT-P varies with the gate voltage;(e) variation of deformation potential constant |E1| and tensile modulus C of NT-P with gate voltage;(f) the carrier mobility of NT-P varies with the gate voltage.
有效质量随栅极电压的变化如图7(d)所示,显然,不管是电子还是空穴的有效质量对栅极电压的改变都不太敏感,数值的变化范围较小,说明栅极电压对带边的色散关系影响不大.弹性模量和形变势常数的变化如图7(d)所示,很明显栅极电压的方向对形变势常数影响较小,但栅极电压大小对形变势常数有较明显影响,表明电子被声子散射的能量改变能被栅极电压调控.弹性模量在施加栅极电压后有明显的减小,这与纳米管总能量随栅极电压变化直接有关,这是因为栅极电压改变了纳米管中的电荷密度分布及静电势分布,从而导致纳米管总能量的变化.最后,可得出NT-P 的载流子迁移率随栅极电压的变化曲线,如图7(f)所示.有趣的是,可以清楚地看出载流子迁移率随栅极电压变化呈“船型”结构,即有几个重要的结论.1) 在较小的栅极电压范围内,例如,在—6—6 V 范围内,纳米管的载流子迁移率变化较小.进一步升高栅极电压,载流子迁移率对电压的敏感性增强,表现出明显上升趋势.例如当栅极电压为18 V 时,电子迁移率为5.8 × 103cm2/(V·s),是未加电压时的3 倍,而当栅极电压为—18 V 时,电子的迁移率为1.8 ×104cm2/(V·s),是未加电压时的10 倍以上.2) 对于空穴迁移率,栅极电压方向对其影响较小,不同于电子的情况.例如当电压为18 V 时,空穴迁移率为3.8 × 103cm2/(V·s),而当电压为—18 V 时,其数值为3.9 × 103cm2/(V·s),相差不多.但这些值相对未加偏压时的空穴迁移率177 cm2/(V·s),增大了近20 倍,显然空穴迁移率比电子迁移率对栅极电压更敏感.3) 如前所述,在零偏压时,掺杂纳米管表现出明显迁移率的载流子极化现象(见图6(c)),在栅极电压作用下,这一现象仍然保持,但在高电压下,这一现象呈现弱化趋势,特别明显的是在18 V,空穴与电子迁移率非常接近.总之,通过改变栅极电压的大小也可以有效改变掺杂纳米管的载流子迁移率,特别是在较高的栅极电压作用下更为显著.
4 结论
基于密度泛函理论的第一性原理计算方法,系统研究了IIIA-VIIA 主族的所有非金属原子低浓度掺杂纳米管后的化学结合特性、电子结构、输运特性及栅极电压调控效应等.计算结果表明掺杂后的纳米管都具有很好的能量稳定性和热稳定性.同时发现:虽然本征纳米管是半导体,但非金属原子掺杂后,纳米管的电子相具有明显的奇-偶效应,即掺杂第IIIA,VA,VIIA 族原子后,纳米管仍为半导体,而掺杂第IVA,VIA 族原子后,纳米管变为金属,这些现象与孤对电子态有密切关系.另外本文计算了不同原子掺杂后半导体性纳米管的载流子迁移率,结果发现载流子迁移率对杂质原子十分敏感,其差值可达1 个数量级.以NT-P 为例,研究了其在栅极电压下的电子性质,特别是载流子迁移率的变化,结果发现杂质原子与纳米管的电荷转移随着栅极电压的改变呈线性关系,且纳米管的带隙随栅极电压的增大而减小,特别是发现纳米管的载流子迁移率对栅极偏压十分敏感,较高的栅极电压能明显提高空穴及电子迁移率,如当栅极电压为18 V 时,空穴迁移率相对未加电压时的情况增加了近20 倍.

