采用改进高斯混合模型的电力客户大数据行为分析

吉 涛，刘玮洁，段 立，郑 伟，廖 勇

(1.国网重庆市电力公司信息通信分公司， 重庆 401120；2.国网重庆市电力公司铜梁供电公司， 重庆 402560；3.重庆大学 微电子与通信工程学院， 重庆 400044)

0 引言

用电客户行为分析是电力大数据研究的重要组成部分，是负荷预测、需求侧响应、电网规划、经济运行、费率制定、能效提升等研究与工作的基础。电力客户行为分析能够为供电企业开拓目标市场，对不同的客户进行差异化定制，提高企业的竞争力。因此，供电企业精准分析出用户用电行为，已成为供电企业经营决策的首要问题。

聚类算法[1-2]是一种将数据集划分为多个不相交子集的数据处理算法，常用的聚类算法包含K-均值聚类(K-means)、高斯混合模型聚类(gaussian mixture model,GMM)、基于密度的带噪空间聚类(density-based spatial clustering of application with noise,DBSCAN)、划分和层次聚类等。其中GMM聚类算法受到较多关注，然而其需要预先知道聚类簇的数量，因此，许多研究对其进行改进。Wang等[3]在高速加工环境下使用GMM来对加工环境进行聚类，对比K-均值聚类算法有着更好的聚类效果。阮晓钢等[4]提出基于GMM最大期望聚类的同时定位与地图构建(SLAM)数据关联算法，通过GMM为观测值进行合理的聚类分组以减少同一时刻参与关联的观测值数量，降低了计算复杂度并提高了算法效率。但上述文献中的算法都采用随机初始化初值，存在收敛速度慢的问题。任莎莎等[5]提出一种结合GMM与K-均值聚类的改进方法，利用K-均值聚类作为辅助，为GMM聚类的迭代过程提供初始的聚类簇中心，并利用期望最大化(expectation maximization,EM)算法进行似然估计，提高了分类的精度，但该方法迭代次数过多，复杂度高。Song等[6]采用GMM仅将EM算法应用新产生的数据，没有充分考虑到历史数据，虽然算法的可行性得到验证，但是聚类簇的数量还是没有确定，且复杂度高。

为进一步提升对用电客户行为分析的效果，针对现有的GMM聚类算法需要知道聚类簇数量以及迭代次数多的缺点，提出联合DBSCAN和EM的GMM算法，简称DEG算法 (DBSCAN-EM-GMM)。该算法主要分为2个步骤：① 采用DBSCAN算法对电力公司所得数据进行第一次聚类，完成k个中心点的选取以及后续高斯模型参数初始化；② 由第一步获得的k个聚类簇中心，利用EM算法迭代GMM的参数，从而有依据地分析数据。此外，对所提算法和其他算法进行对比，论证了所提算法的可行性和有效性。

1 DEG算法

基于DBSCAN的聚类算法和EM算法作为基础的GMM聚类算法，构建了DEG算法。整套算法先通过DBSCAN聚类算法进行第一次聚类来寻求合适的聚类数目k以及后续GMM算法的初始参数，然后采用EM算法进行迭代求解GMM模型的参数，算法构建的基本流程细化如下：

设电力公司的客户信息数据x有n个特征，定义x=[x1,x2,…,xn]T，假定x服从式(1)分布：

(1)

该分布由k个高斯分布成分组成，其中δi表示来自第i个高斯分布的概率，满足式(2)关系：

(2)

p(x|μi,Ti)为x的概率密度分布函数，其定义如式(3)所示：

(3)

其中，μi为均值向量，Ti为协方差矩阵，(·)T为转置运算。式(3)指出该分布的参数由均值向量和协方差矩阵组成。为了便于分析，引入隐变量p(yj=i)[7]，注意p(yj=i)=δi，其含义为样本xi是来自第j个高斯分布成分的概率，当满足式(4)条件时，视xj为来自第i个高斯成分：

maxp(yj=i),j=1,2,…,k

(4)

当隐变量已知时，高斯混合聚类模型将数据集D={x1,x2,…,xm}划分成k类数据，此时为了得到模型参数(δi,μi,Ti)，需要采用最大似然估计法求解参数，数据集D的似然函数如式(5)所示：

(5)

对L(D)取对数可以得到对数似然函数，如式(6)：

(6)

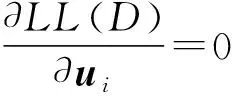
(7)

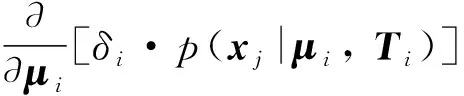
δi·p(xj|μi,Ti)·(xj-μi)]

(8)

(9)

令式(9)等于0，则μi为：

(10)

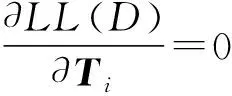
(11)

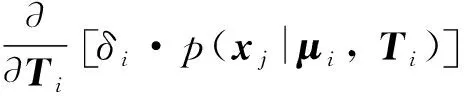
(12)

代入式(11)，可得到Ti为：

(13)

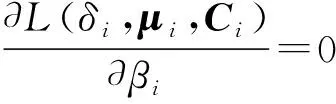
(14)

(15)

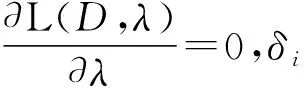
(16)

上述推导得到μi、Ti及δi的计算过程，当这3个参数计算后，反过来更新后验概率p(yj=i|xj)，根据贝叶斯公式，可以得到式(17)：

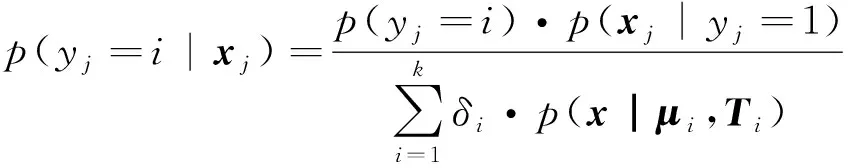
(17)

EM算法[8]的过程分为2步：在初始化模型参数(δi,μi,Ti)后，首先根据式(17)计算各分模型的概率，其次根据式(10)(13)和(16)更新3个模型参数，并反复迭代，直到似然函数增长缓慢或不再增长为止。然而初始化的参数决定着迭代次数，如果初始化的参数选取不恰当，会导致大量的迭代，直接影响着聚类过程的效率。通常初始化的方法采用随机选取的方式，即随机抽取k个点作为聚类中心，并计算剩余的m-k个数据与这k个点的距离，根据距离最近的准则划分数据的类别。完成划分后，得到k个类别的所有数据，并计算初始参数(δi,μi,Ti)，之后进行EM算法的迭代。随机选取聚类中心的方式并不能保证收敛速度，甚至可能造成收敛缓慢，因此，本文提出基于DBSCAN[9]的初始化方式，一方面DBSCAN基于密度的方式进行聚类较随机选取的方式相比能够加速EM算法的迭代，另一方面DBSCAN能够自动确定k值，解决高斯聚类需要提前知道k值的难题。DBSCAN聚类过程如算法1所描述。

算法1：用于初始化高斯聚类初值的DBSCAN聚类

输入：D={x1,x2,…,xm}，r，P

过程：

1． Ω=∅

2． forj=1,2,…,n

3． 统计与xj的欧式距离小于r的数据个数Pj

4． ifPj≥P

5． Ω=Ω∪{xj}

6． end if

7． end for

8．o=1

9． while Ω≠∅

10． 随机从Ω中选取一个对象xi

11． 寻找所有xi密度可达的数据{xl,xl+1,…}

12． 形成聚类簇Co={xi,xl,xl+1,…}

13． if {xj,xj+1,…}⊆Coand {xj,xj+1,…}⊆Ω

14． Ω=Ω/{xj,xj+1,…}

15． end if

16．o=o+1

17． end while

输出：聚类簇划分C={C1,C2,…,Ck}

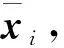
算法2：DEG聚类

输入：D={x1,x2,…,xm}，r，P

过程：

1． 根据算法1得到初始聚类簇C={C1,C2,…,Ck}

2． 选取k个聚类簇的中心{x1,x2,…,xk}，并初始化 {(δi,μi,Ti)|i∈[1,k]}

3． while ΔLL(D)≤ε

4． forj=1,2,…,m

5． 根据式(17)更新p(yj=i|xj)

6． end for

7． fori=1,2,…,k

8． 根据式(10)更新μi

9． 根据式(13)更新Ti

10． 根据式(16)更新δi

11． end for

12． end while

13． forj=1,2,…,m

14． 对于xj，选取最大的p(yj=i|xj)，i∈[1,k]

15．xj∈Ci

16． end

输出：聚类簇划分C={C1,C2,…,Ck}

2 聚类算法评价指标

目前存在许多聚类算法的评价指标，选取其中典型的指标对聚类算法进行性能评价，包括Fowlkes-Mallows (FM)[10]，调节兰德指数(adjusted rand index,ARI)[11]，Jaccard系数(jaccard coefficient,JC)[12]以及分离度(degree of separation,DS)[13]等。

FM指标的计算表达式为：

(18)

其中:a是2个同类样本点在同一个簇中的个数，b表示2个非同类样本点在同一个簇中的个数，c表示2个同类样本点分别在2个簇中的个数。FM指标在0～1，当FM指标大的时候，说明划分后的簇与标准簇较为接近，当FM指标为1时说明聚类的结果完全正确，与标准簇一致。

ARI是兰德系数(rand index,RI)的改进，较后者相比，ARI系数能去掉随机标签对评估结果的影响，其计算公式如式(19)所示：

(19)

其中，d表示2个非同类样本点分别在2个簇中的个数，ARI取值在-1～1，越大表示聚类效果越好。

Jaccard系数描述了样本集的异同性。其系数越大说明样本的相似度越高。其定义如下：

(20)

其中，JC位于0～1，值越大越好。

分离度簇与簇之间的分离程度，分离度越高说明簇之间的分离程度越清晰。如式(21)和式(22)所示：

Fij=(uij-α)2

(21)

(22)

其中，Fij表示模糊偏差，uij为数据j对第i类的支持度，其值越大就说明它的信息量越大，α为惩罚因子，默认取值为0.5。簇之间的模糊偏差相乘表示2个模糊集合的分离度，分离度就越高，取值越小。

将所有子簇的分离度相加得到总体分离度，其计算方法如式(23)所示：

(23)

3 应用案例

3.1 数据准备

数据准备即从客户端大数据中选取对聚类结果影响较大的特征作为聚类分析的数据基础和用电行为分析的主要对象。

1)特征属性的选取

对用电客户的客户行为和性质进行分析，形成了一个指标体系来判断用户行为规律和区分用户类别，从而帮助管理者改进服务以及优化业务。在表1中，基于聚类的特点，对客户的行为数据进行划分，包括客户消费水平，客户掉电敏感程度，欠费风险以及设备风险，分别反映了客户的消费水平、客户对于用电需求的紧急程度、客户的诚信度以及客户的安全意识。这些指标能全面分析客户的行为特点和规律。

表1 客户行为评估因素

2) 数据采集

此次一共选取了20 000位客户的对应数据，选取标准为前面整理出的客户分群的评估因素，一些客户的消费水平信息如表2所示。

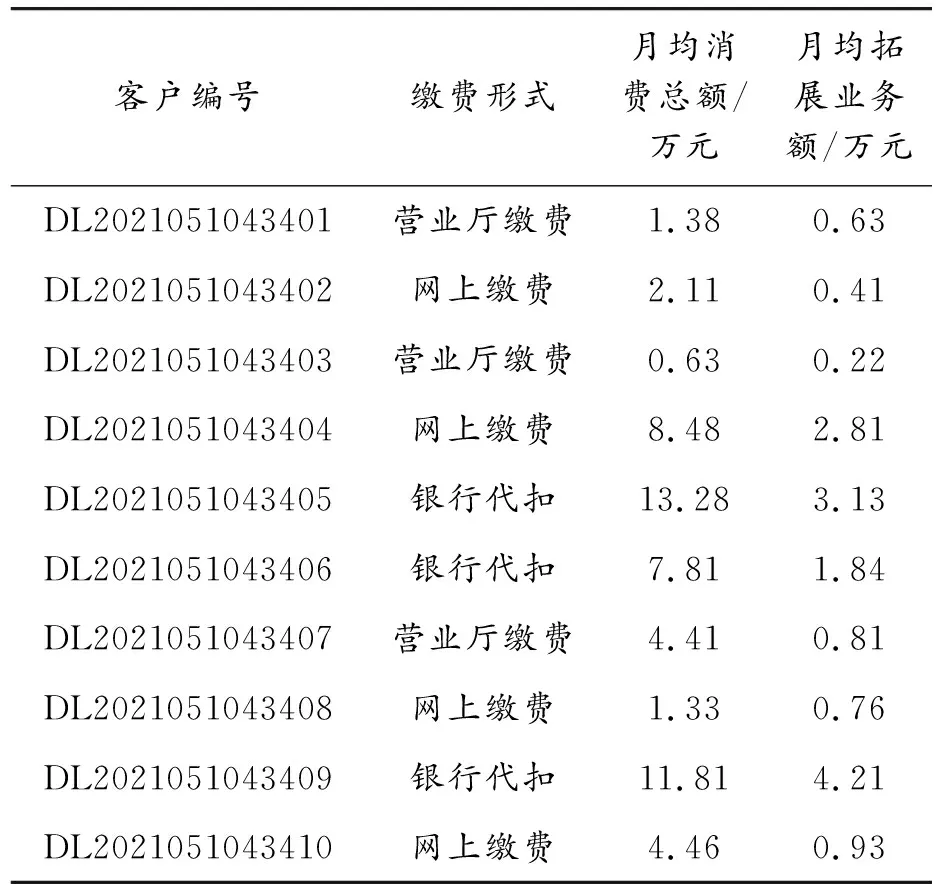
表2 用户消费水平信息

由用电类型、掉电后的投诉数量以及签订的合同容量共同组成了客户掉电后敏感程度信息，信息示例如表3所示。

为了能够比较精确的看出客户缴费是否及时，选取了几项指标来构成客户欠费风险信息，如表4所示。

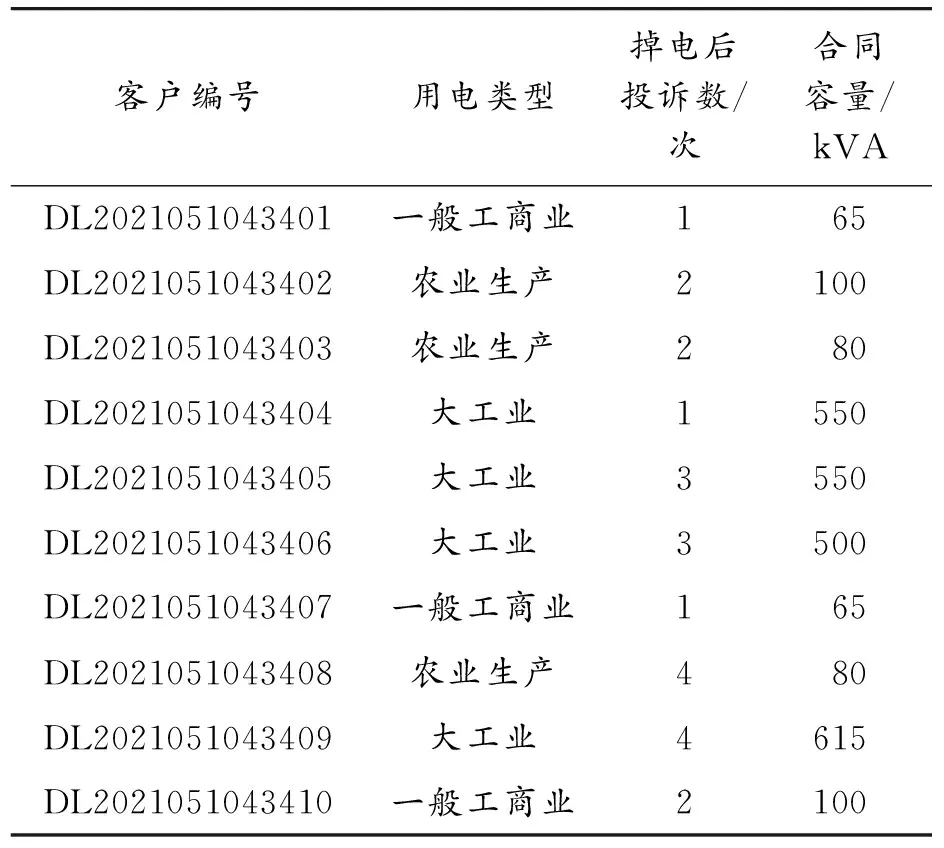
表3 客户掉电敏感程度信息

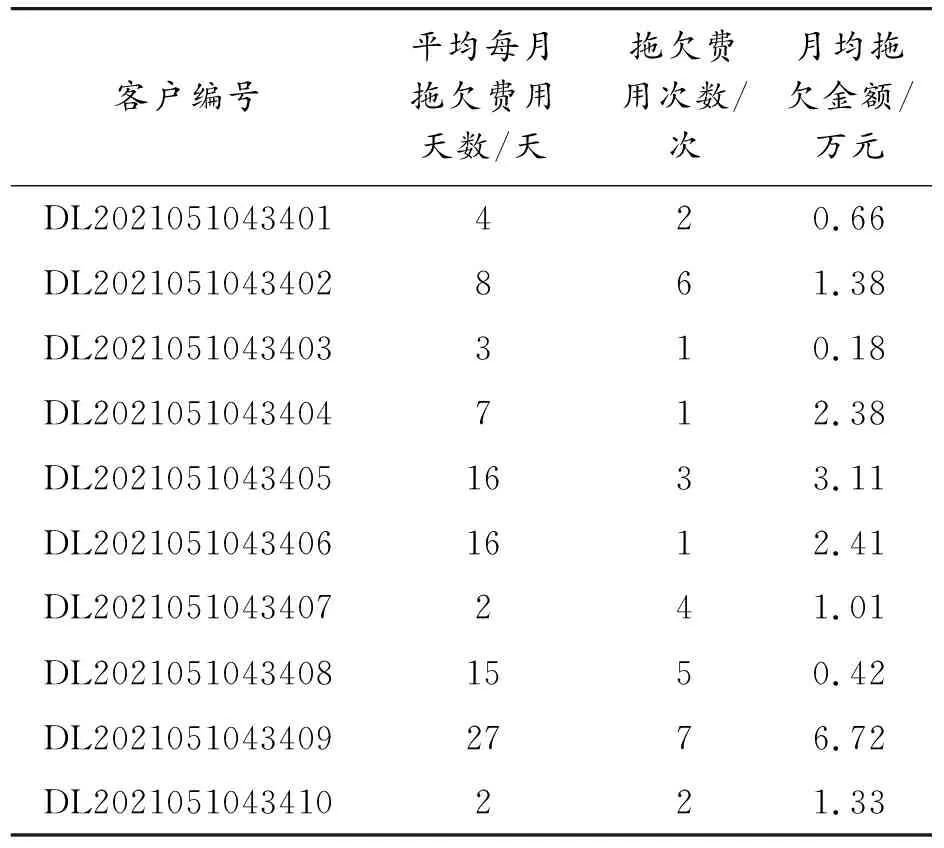
表4 客户欠费风险信息

表4展示的是部分客户的客户盗电风险各项指标的数据。根据实际用电量以及合同用电量来计算匹配度λ，如式(24)所示。

(24)

3.2 聚类结果

本文对比了上文所提的采用DBSCAN聚类初始化和采用随机选取初始化的测试结果。图1为未聚类之前的数据分布情况，图2为随机选取初始化的聚类中心以及其余数据的分布情况，图3为采用DBSCAN初始化方式的聚类中心以及其余数据的分布情况，图4为最终聚类结果。从最终的结果可以看出，数据集被分为3类。随机选取初始化的方式迭代次数为514次，而采用DBSCAN初始化仅需要26次迭代。从图2可以看出，随机选取的3个中心与最终的聚类中心差距较大，由于这点，其余数据的聚类簇化分也与最终的聚类簇有较大差距，因此需要大量的迭代次数来调整参数。

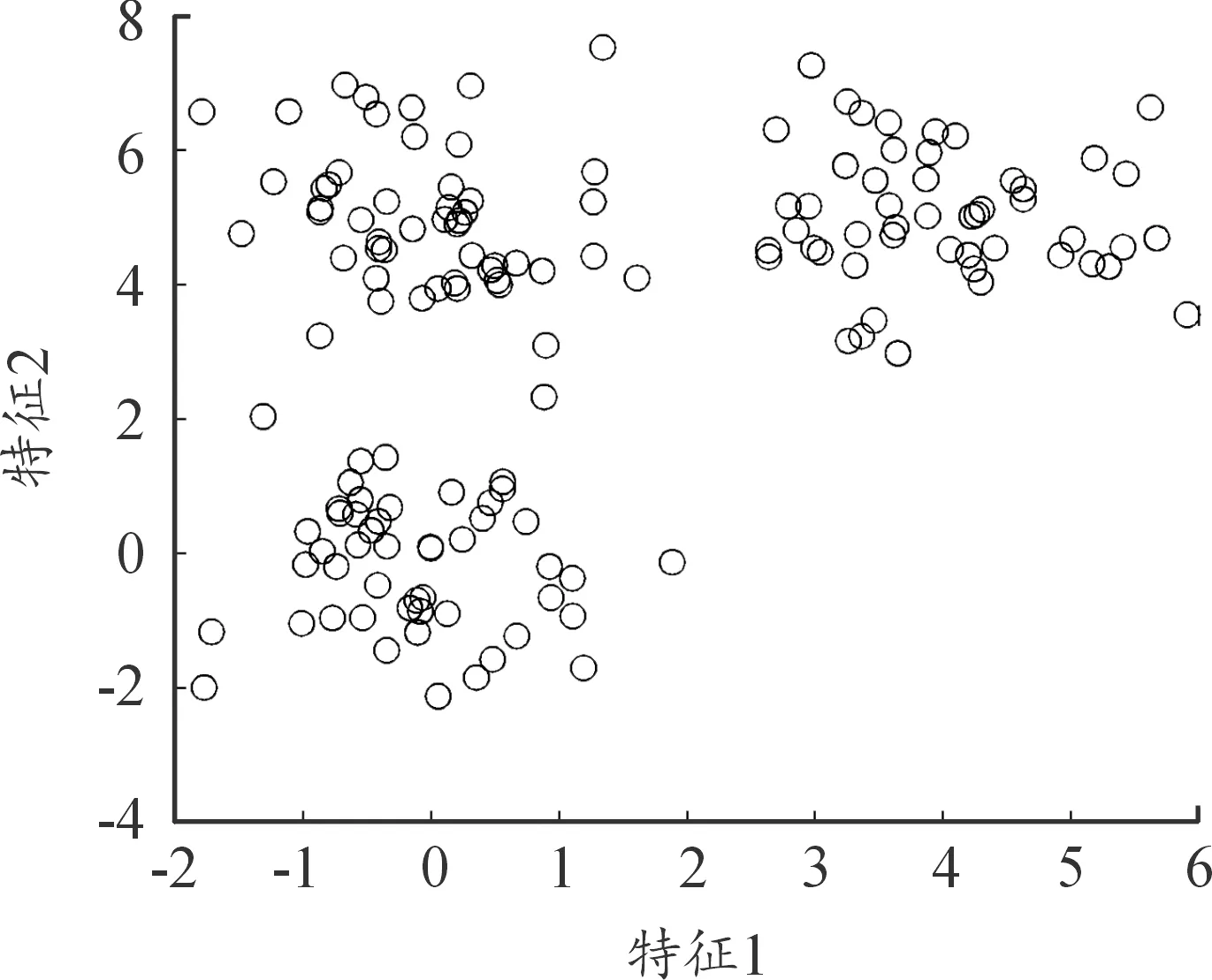
图1 数据分布

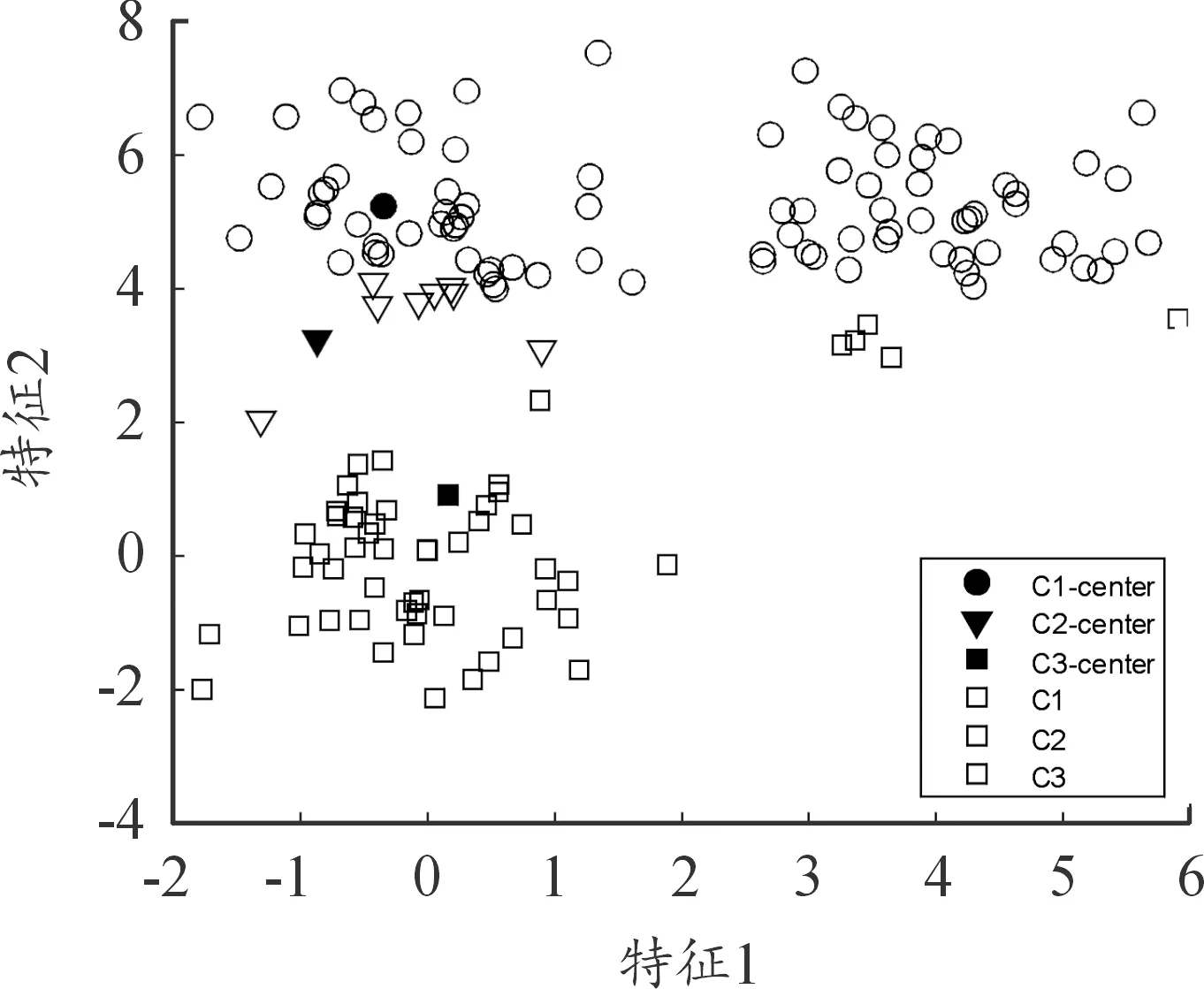
图2 随机选取初始化

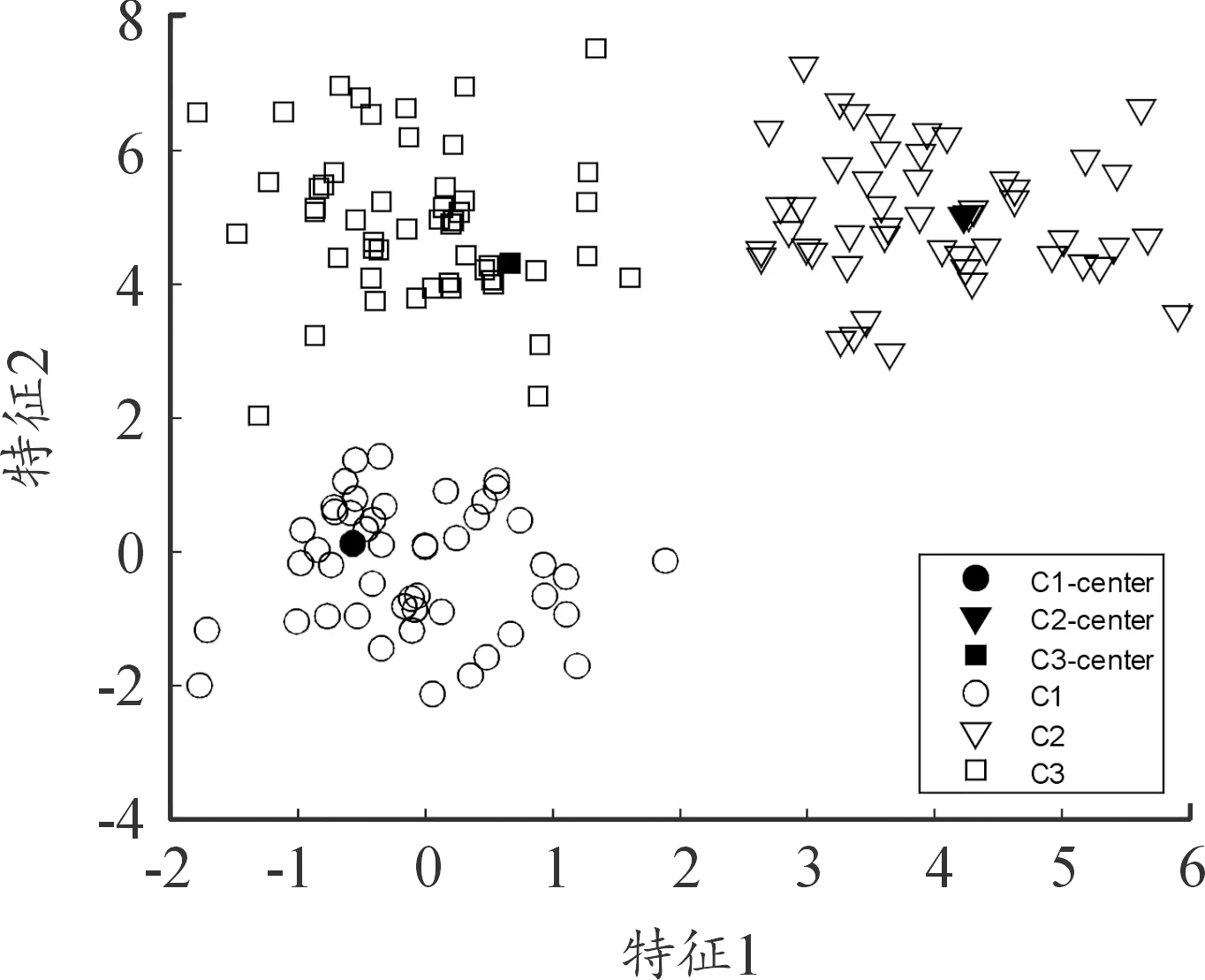
图3 DBSCAN初始化

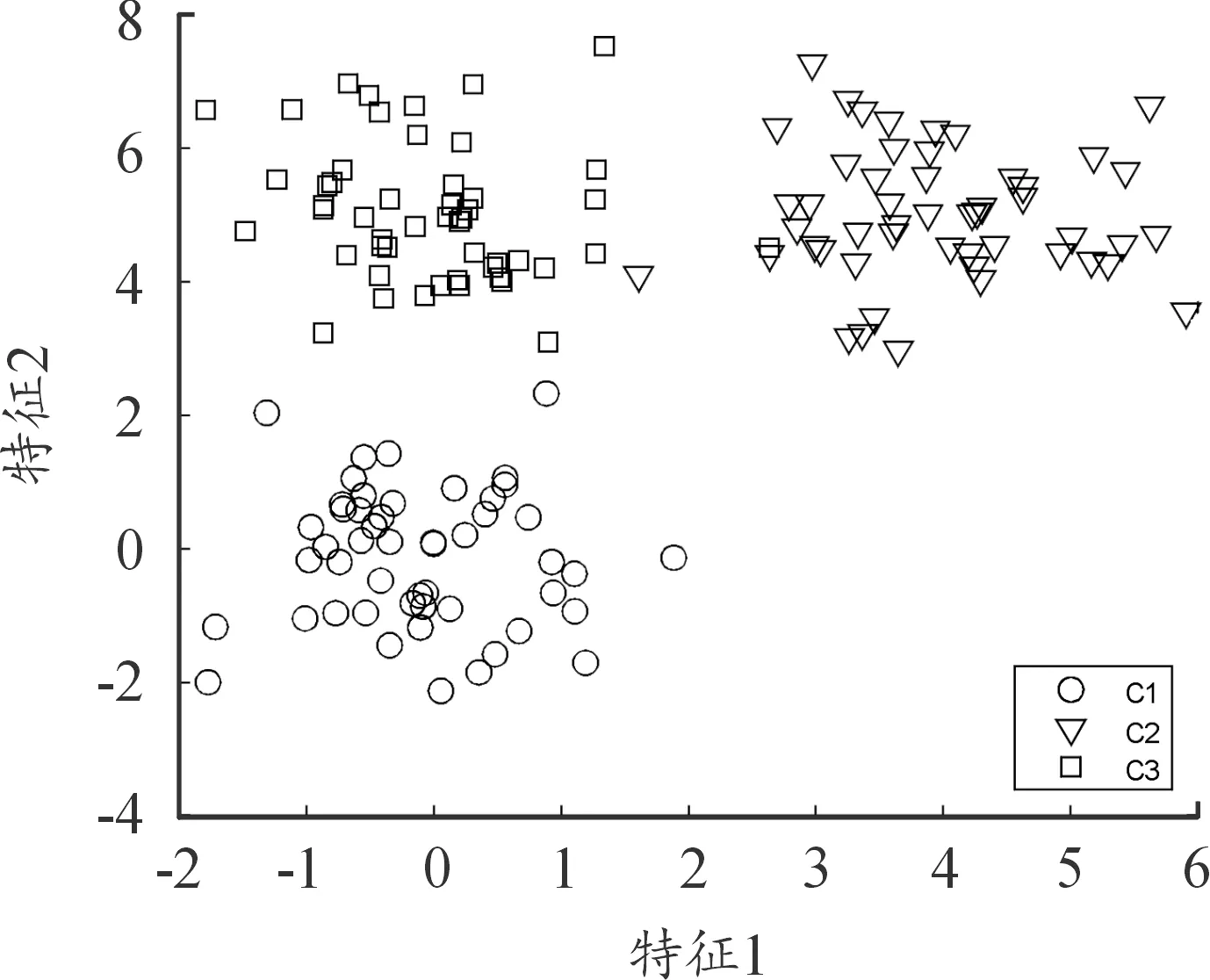
图4 聚类结果

图3采用DBSCAN初始化在一开始就能找出与最终结果接近的聚类簇，虽然有个别的数据存在偏差，但是经过少量迭代调整之后就能得到最终的聚类结果。

通过聚类的结果分析不同类型客户大致的用电行为，通过对表5的数据，可以得出通过本文客户行为分析算法，最终将客户分为了三大类，下面通过该数据对每一类客户具体分析：

第1类客户群：此类客户占到了总客户数的40%，拥有很高的比重，并且月均消费也是三类客户中最高，达到了13.87万元，对电力公司的影响较大；另外，该类客户的合同容量为550 kVA，用电匹配度为0.97，对于用电容量还是有较高要求的，用途多为大工业用电，并且该类客户的安全用电意识整体来说比较高；需要注意的是该类客户的电费拖欠比较严重，金额为4.48万元。总体来说，该类客户属于具有高水平价值的客户。

第2类客户群：此类客户占到了总客户数的50%，说明这是其中最广泛的客户，该类客户的消费水平较低，月均消费为1.48万元；合同容量也仅为75 kVA，对用电容量的需求不是很高，用电匹配度为0.87，所以用途大多数是工商业用电，并且该类客户的安全用电意识整体来说良好；不过拖欠金额为0.37万元，说明此类客户的信用较好，拖欠情况不是很严重。总体来说，该类客户属于具有中等水平价值的客户。

第3类客户群：此类客户比重仅仅为总客户的10%，属于客户数量中较少的群体。该类的消费水平属于中等水平，月均消费为4.15万元。另外，该类客户的合同容量为110 kVA，用电匹配度为0.71，对于用电容量要求一般，并且该类客户的安全用电意识整体来说较差；拖欠金额3.87万元，拖欠情况较为严重，诚信度较低。总体来说，该类客户属于具有较低水平价值的客户。

表6描述了3种算法在相同数据情况下的性能。从表中可以看出，高斯聚类算法的指标优于K-均值算法，然而在运行效率上，K-均值算法的速度为高斯聚类算法的一半。本文所提的算法基于高斯聚类算法改进，因此指标进一步提升了，且由于在迭代之前进行了良好的初始化，因此运行时间也得到了较大的提升。

通过本文的聚类算法对数据进行分析获得聚类结果，利用本文所提的聚类算法可以对客户端大数据进行分析并获得聚类结果，电力企业通过对聚类结果进行用电客户进行行为分析和客户分类，从而针对不同类型的客户采取不同的措施和营销策略，以提升工作效率，并同时让不同的用电客户有更好的用电服务体验。此外，电力企业不仅能在服务上进一步拓展广度及深度，在精细化运营管理以及需求侧管理水平上能得到进一步的提升，还为后续智能电力需求提供了数据上的支持。

表5 聚类结果

表6 聚类质量测试结果

4 结论

提出DEG聚类算法用于对电力客户聚类，该算法基于DBSCAN聚类算法进行第一次聚类，在此过程中确定聚类中心的数目以及后续迭代时所需的初始值，通过这些值进行EM算法的GMM聚类，其中DBSCAN算法不仅解决了高斯混合聚类的k值问题，而且能够加速EM算法的迭代，增强聚类的全局寻优能力。案例中，采用了FM、ARI、JC、DS聚类质量评价以及运行时间作为指标，对比现有的K-均值算法与基于随机初始化的GMM算法，本文算法的聚类效果、聚类质量以及全局寻优能力更好，且稳健性良好。