计及身管柔性补偿的高速机动坦克炮口振动仿真与控制研究

陈 宇， 杨国来， 孙全兆， 周宏根， 刘金锋

(1.江苏科技大学 机械工程学院，江苏 镇江 212100；2.南京理工大学 机械工程学院，南京 210094)

火炮炮口振动会影响弹丸出炮口姿态，是影响火炮射击精度的关键因素，而火炮身管具有较大的长径比，在自重、发射载荷和随机外激励耦合作用下产生强烈的非线性柔性振动，严重影响火炮炮口的振动响应[1-2]。因此，身管的振动特性和振动补偿方法一直是火炮发射动力学研究的热点问题[3-4]。目前，控制身管柔性振动影响的方法主要包括两种：优化设计方法和身管振动主动控制方法。其中，优化设计方法是一种被动控制方法，已有研究表明，通过对身管结构、刚强度等进行多目标优化设计可以在一定程度上改善身管的动态性能[5-7]，但该方法的控制效果受外部因素的影响较大，当外部激励发生变化时，优化设计的效果降低明显。身管振动主动控制方法一般通过在身管上添加压电作动器等主动控制机构，实现对身管振动的控制[8-9]。其可在不同外部激励下有效减小炮口振动，但实现较为复杂，成本较高。

坦克作为具有行进间射击能力的一种直瞄火炮，普遍装备了能够控制坦克炮运动的坦克稳定器[10]。现有坦克稳定器一般以摇架耳轴中心的角位移为控制目标，为稳定器提供系统输入的测量火炮运动状态的角度陀螺仪及角速度陀螺仪等都安装在摇架上。虽然自适应控制[11-13]、迭代学习控制[14-15]、重复控制[16]、鲁棒控制[17-18]等现代智能控制算法被逐渐应用于稳定器控制方法设计中，但仅能补偿稳定器执行装置中的非线性和不确定性等对坦克炮振动控制精度的不利影响，而无法有效补偿身管柔性、运动副间隙等火炮系统结构非线性因素的影响。显然，在坦克稳定器控制器设计中考虑身管柔性等火炮结构非线性因素对炮口振动的影响是一个较优的替代方案。

基于此，本文构建了考虑身管柔性的坦克行进间机电液耦合动力学模型，通过数值计算分析了身管柔性等火炮结构非线性因素对稳定器控制性能的影响。并进一步提出了将炮口中心角位移作为稳定器误差补偿信号的炮口振动控制方案，构建了考虑身管柔性的炮口误差信号补偿模型，通过与原有控制方案的比较表明，改进后的控制方案可有效减小身管柔性等火炮自身非线性因素对炮口振动的不利影响，有利于提高坦克垂向稳定器的综合稳定效果。

1 坦克行进间机电液耦合动力学建模

坦克是由机械、液压及控制子系统共同协作的复杂系统，本文分别基于仿真软件RecurDyn、Amesim及MATLAB/Simulink实现坦克行进间机、电、液各子系统的建模。建模中，主要考虑了耳轴轴承间隙、身管衬瓦间隙及身管柔性等结构非线性因素[19]。并基于谐波叠加法编写了考虑左右履带不平度相干性的符合我国路面不平度分级标准的D级三维路面谱文件[20]。

坦克垂向稳定器通过控制液压杆的运动使火炮失调角θc近似为零，从而保证坦克行进间火炮的稳定性。当以摇架耳轴中心的高低角位移为坦克垂向稳定器的实际控制目标时，根据图1中火炮身管与液压缸安装位置关系，液压杆预期位移y1d可由下式计算求得(当θc=0时)

(1)

(2)

式中：α为图1中显示的液压缸对应的顶角角度；θs为瞄准角，本文研究中取θs=0；l为θs=0时液压缸的初始长度；a为耳轴中心点与液压缸在炮塔安装位置的距离；Δl为液压缸的伸缩长度。

图1 液压缸安装位置图Fig.1 Installation location of hydraulic cylinder

本文定义系统状态变量为

(3)

式中：y为液压缸输出位移；P为液压缸两腔压差(P=P1-P2)；A为液压缸有效活塞面积。则坦克垂向稳定系统电液位置伺服系统的数学模型可表示为

(4)

(5)

(6)

式中：m为活塞以及负载所等效到活塞上的总质量；ft为液压缸外负载；B为有效黏性阻尼系数；Af为可建模的库仑摩擦幅值；Sf为连续的近似库仑摩擦形状函数；dn为未建模动态；β为液压油弹性模量；V1、V2分别为系统两控制腔容积；Q1、Q2分别为由伺服阀进入、流出液压缸的液压流量；Ct为执行器泄露系数；g为相对于控制输入的流量总增益；Ps、Pr为系统油源压力和回油压力；s(u)为符号函数；u为控制输入信号。

根据已有研究基础，采用自适应鲁棒控制算法，设计如下的坦克稳定器控制器

(7)

(8)

(9)

θ=[θ1，θ2，θ3，θ4]T=[B,Af,ft,Ct]T

θ∈Ωθ{θ:θmin≤θ≤θmax}

(10)

利用C语言将设计的自适应鲁棒控制器编译为Simulink系统能够识别的S函数形式，并将其整合进坦克行进间机电液耦合动力学模型中。本文建立的坦克行进间机电液耦合动力学模型如图2所示。

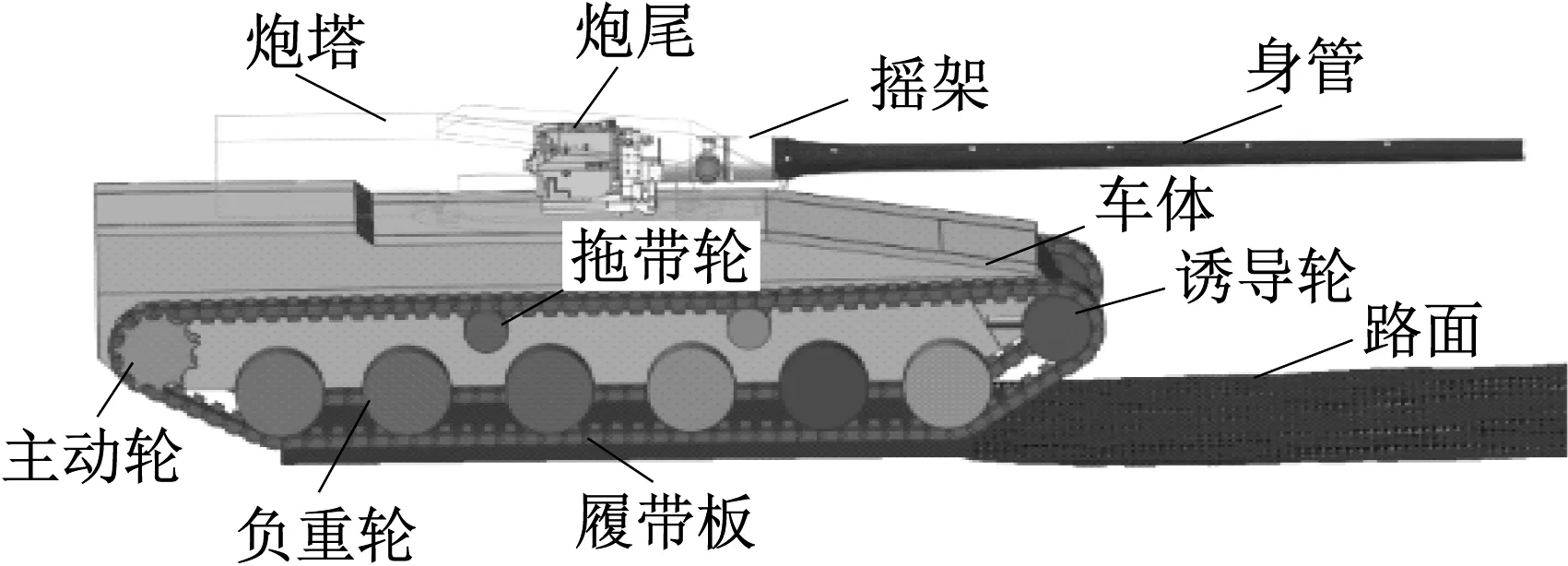
图2 坦克行进间机电液耦合动力学模型Fig.2 The mechanical-electrical-hydraulic co-simulation model of the moving tank

2 坦克行进间炮口振动分析

通过对坦克在D级路面上以20 km/h速度行驶时的火炮振动响应进行数值计算，得到自适应鲁棒控制器作用下，坦克行进间液压杆位移的实际值与预期值对比如图3所示，其中，自适应鲁棒控制器参数的设置如表1所示。

(a) 实际值与预期值对比图

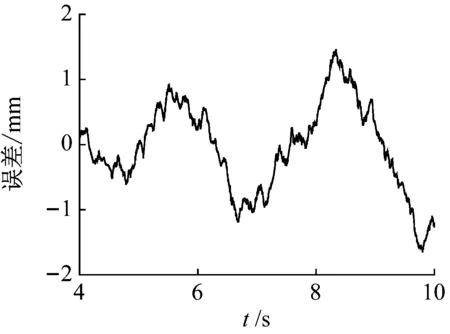
(b) 跟踪误差图图3 液压杆位移图Fig.3 The piston displacement

表1 自适应鲁棒控制器参数Tab.1 Parameters of adaptive robust controller

由图3分析可知，在整个坦克行驶过程中，液压杆的实际位移能够较好地跟踪预期位移，位移曲线变化趋势一致，跟踪误差极值仅约为1.65 mm。同时，由图4自适应鲁棒控制器作用下坦克行进间摇架高低角位移曲线可知，在自适应鲁棒控制器作用下摇架处的高低振动幅值显著减小为2.38 mrad，摇架处的垂向稳定精度约为0.82 mrad。因此，按照传统坦克稳定器设计要求可以认为设计的垂向稳定器控制器能够有效控制坦克行进间火炮的振动。

图4 坦克行进间摇架高低角位移Fig.4 The cradle elevation angular displacement of the moving tank

然而，坦克火炮身管是一个长径比很大的、壁厚很薄的中空圆柱体，其类似于悬臂梁结构。在自重因素影响下，身管会发生明显的变形弯曲。由静平衡计算可得，身管自重弯曲状态下，炮口垂向角位移约为-4.49 mrad。在身管衬瓦间隙的耦合影响下，摇架耳轴中心的高低角位移与炮口中心的高低角位移并不可能相同。图5给出了自适应鲁棒控制器作用下，坦克行进间炮口与摇架处高低角位移对比。结合表2可知，炮口高低角位移在数值上相较于摇架处整体偏小，炮口处垂向稳定精度较摇架处降低了559.76%。对于常规静止间射击火炮而言，可通过调整火炮射角补偿这一误差。但如图6所示，坦克行进过程中身管会发生非常复杂的柔性振动，同时，由表2可知，炮口处高低角位移的标准差为5.50 mrad，相较于摇架处提高了444.55%。显然，其难以通过调整火炮射角实现有效补偿。因此，虽然设计的坦克稳定器控制器对摇架振动控制效果明显，但炮口指向与预期瞄准角之间偏差依旧较大，难以保证行进间的射击精度，这是由于在根据式(1)、(2)计算液压杆预期位移时，忽略了火炮系统自身非线性因素的影响，其被简单看作为一个线性系统。

图5 坦克行进间摇架和炮口高低角位移对比图Fig.5 Comparison between the elevation angular displacement of cradle and muzzle

表2 摇架和炮口高低角位移统计值对比Tab.2 Comparison between the elevation angular displacement of cradle and muzzle

图6 弹丸膛内运动时期身管高低方向弯曲状态图(变形量放大100倍)(mm)Fig.6 The barrel bending states in the vertical direction during the motion of the projectile in-bore (deformation magnified by 100 times) (mm)

3 炮口误差信号补偿建模与计算

在上文对坦克行进间炮口振动影响因素分析的基础上，本文提出将炮口中心角位移作为误差补偿信号加入到设计的垂向稳定器控制器中，以期减小坦克行进间摇架耳轴中心与炮口中心高低角位移间的差异对射击精度的不利影响，则修正后液压杆预期位移的计算公式可表示为

(11)

(12)

式中：φ为炮口中心与摇架耳轴中心间高低角位移的差值，其主要由身管柔性及身管衬瓦间间隙等火炮结构非线性因素引起。该差值在数值计算过程中可通过位移函数从动力学模型中直接读取，而在实际坦克系统中则可通过在炮口处安装角陀螺测量炮口角速度，并通过计算后传递至火控计算机。将该公式嵌入到控制器中，控制器的控制律及控制参数与前文相同。

为分析加入炮口误差补偿信号后坦克垂向稳定器的控制效果，同样对坦克在D级路面上以20 km/h速度行驶时的火炮振动响应进行数值计算。图7为加入误差补偿信号后自适应鲁棒控制器的跟踪误差。由图7(b)可知，修正后的控制器跟踪误差较小，极值为2.43 mm。其与图3中跟踪误差相近，说明加入炮口误差补偿信号对控制系统稳定性影响不大，本文引入自适应鲁棒控制方法设计的坦克垂向稳定器控制器跟踪性能变化在可接受范围之内。

(a) 实际值与预期值对比图

(b) 跟踪误差图图7 加入补偿信号后的控制器跟踪误差Fig.7 The tracking error of the controller with error compensation signal

图8为加入补偿信号后的坦克行进间炮口高低向角位移曲线，结合表3所示，炮口在瞄准角附近振动，加入补偿信号后炮口垂向角位移极值由8.08 mrad减小为3.61 mrad；炮口处垂向稳定精度由5.41 mrad提高至1.17 mrad；炮口垂向角位移标准差由5.50 mrad减小为1.38 mrad。与图5比较可知，由火炮自身非线性因素造成的坦克行进间炮口高低角位移整体小于摇架处，以及炮口振动幅度大于摇架处，影响稳定器稳定效果的问题得到了有效控制。说明本文提出的在控制器设计中考虑火炮结构非线性因素影响，利用炮口中心角位移作为垂向稳定器控制器误差补偿信号的方法是可行且有效的。

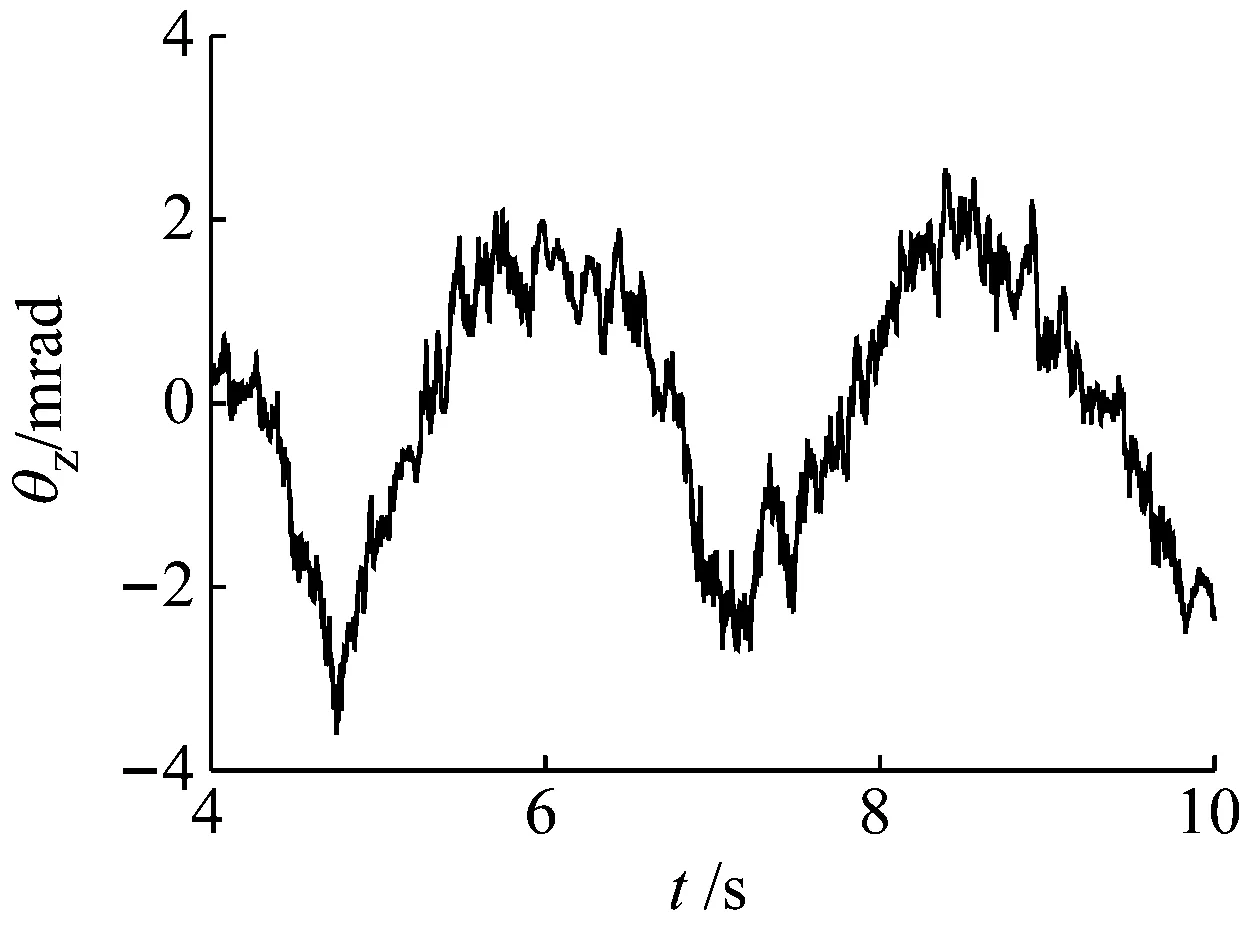
图8 加入补偿信号后的炮口高低向角位移Fig.8 The muzzle elevation angular displacement with error compensation signal

但是，由图8还可看出，炮口高低向角位移信号中含有更多的高频振动分量，这是由于加入的误差补偿信号φ中含有更多高频成分，这在图7跟踪误差中也有体现，显然这同样会影响坦克行进间射击的射击精度，需要进一步研究控制，这将是今后工作的重点之一。

表3 加入补偿信号前后炮口高低向角位移Tab.3 The muzzle elevation angular displacement with or without error compensation signal

4 结 论

本文基于动态协同仿真方法，构建了考虑身管柔性的坦克行进间机电液耦合动力学模型，仿真、分析并抑制了身管柔性等火炮结构非线性对坦克垂向稳定控制效果的影响。主要研究结论包括：

(1) 由于身管衬瓦间隙以及身管柔性等火炮自身结构非线性因素的影响，坦克行进间炮口中心高低角位移与摇架处差异较大，造成稳定器控制性能降阶明显，影响坦克行进间射击精度。

(2) 提出在控制器设计中考虑火炮结构非线性因素影响，通过将炮口中心角位移作为稳定器误差补偿信号加入设计的控制器中，可有效减小火炮自身非线性因素对炮口振动的不利影响，提高坦克垂向稳定器的综合稳定效果。

本文对坦克行进间火炮结构非线性与稳定器的耦合振动特性与控制进行了初步探索性研究，研究可为坦克炮稳定器设计及炮口振动控制研究提供参考，但现有研究还较为简单，且仍需进一步得到试验的验证。