基于振动感知的油浸式电抗器松动故障检测方法

高树国， 张明文， 吴书煜， 孟令明， 汲胜昌

(1.国网河北省电力有限公司电力科学研究院，石家庄 050021；2.国网河北省电力有限公司，石家庄 050021；3.西安交通大学 电力设备与电气绝缘国家重点实验室，西安 710049)

高压并联电抗器作为电力系统抑制工频电压升高和无功补偿的关键设备[1-2]，得到了广泛应用。与变压器类似，电抗器同样具有绕组铁芯结构且存在着多气隙铁芯饼的特殊结构[3-4]，因而造成了振动大噪声强的问题，在长期运行过程中，容易造成内部结构件及自身铁芯绕组松动，以致加剧振动，长此以往，恶性循环，最终导致电抗器因振动过大而停运，甚至造成严重事故[5]。研究电抗器振动特性，在出现内部机械故障后快速做出诊断，对保证电抗器安全稳定运行具有重要意义。

目前，在已有变压器振动研究的基础上，国内外学者开展了大量关于电抗器振动特性的研究，主要集中在建模仿真研究与试验测试研究[6-8]。在建模仿真研究方面，文献[9]考虑电抗器振动产生的起因、经过和结果，通过多物理场耦合的方法研究了电抗器振动噪声分布规律；文献[10]提出了涉及铁芯叠片规则的流-固耦合的电抗器铁芯振动计算方法；文献[11]考虑磁致伸缩效应与绕组受力，建立了电抗器三维模型，计算并分析了本体振动特性。在试验测试研究方面，文献[12]测试了三台并联电抗器振动，提出了现场优化电抗器振动的方法；文献[13]通过绘制电抗器各表面振动云图，发现因结构的差异性造成振动的不对称性；文献[14]计及ΔE效应，分析了电抗器铁芯振动特性。以上研究从理论与实验两方面研究了电抗器本体振动特性和规律，随着信息处理技术的飞速发展，应用感知终端的多源数据分析的方法对电抗器状态进行评估成为一种有效的手段，也为基于振动法对电抗器进行故障分析与诊断提供了一定的基础。

本文以一台10 kV高压并联电抗器为振动研究对象，分析了包括正常与不同程度松动在内的四种工作状态。通过振动云图分析了电抗器油箱表面振动幅值分布规律；应用最小二乘法与R-square确定了最佳测点；采用EMD分解与重构、计算欧氏距离与频谱复杂度，形成了振动特征矩阵，以随机森林法对电抗器状态做出判断，提出基于多信息融合的电抗器故障检测与诊断方法，实现了对电抗器内部机械状态的准确分类。

1 电抗器振动测试平台的搭建

1.1 振动测试平台

电抗器振动测试平台主体设备由电源、调压器、变压器以及高压并联电抗器组成，整个试验平台能够完成电抗器振动特性研究以及典型机械故障模拟，振动测试平台整体示意图如图1所示。三相电源为整个系统提供电能，调压器提供连续可调电压，变压器起到升压作用，高压并联电抗器主要参数如表1所示。

图1 高压并联电抗器振动测试平台示意图Fig.1 Schematic diagram of the high voltage shunt reactor vibration test platform

1.2 振动试验

电抗器振动试验采用压电式加速度振动传感器采集油箱表面振动信号方式，加速度传感器通过磁铁牢牢吸附在油箱表面，分辨率为100 mV/g(其中，g为重力加速度9.8 m/s2)，具有重量轻、量程大的特点。为全面研究不同测点振动特性以及选择最优测点，同时充分考虑电抗器铁芯绕组结构位置与油箱尺大小，对油箱表面划分多个单元，分为9行8列，从最上面一行开始为第1行，最左边为第1列，依次命名为(1,1)、(1,2)…(9,7)、(9,8)，图2为振动测点图。

表1 高压并联电抗器主要参数Tab.1 Main parameters of the high voltage shunt reactor

图2 电抗器油箱表面振动测点Fig.2 Vibration measurement points diagram of reactor oil tank surface

振动试验分为升压试验与故障试验。升压试验按照变压器一次侧相电压20 V步长电压等级进行升压，分别施加在电抗器侧电压为4.76 kV、5.63 kV、6.50 kV、7.36 kV、8.23 kV、9.09 kV、10 kV、10.87 kV。根据电抗器实际运行过程中出现的机械问题，故障试验通过松动螺杆模拟铁芯绕组同时松动故障，并将额定预紧力、松动4 N·m、松动8 N·m、松动12 N·m即正常状态、松动25%、松动50%和松动75%四个梯度的状态，分别对应为状态1、状态2、状态3、状态4。

2 振动测点选择

2.1 振动测点选择模型

电抗器本体振动是由铁芯和绕组造成的。铁芯在磁致伸缩效应与麦克斯韦力作用下产生振动，且由于油浸式并联电抗器铁芯柱的特殊结构，铁芯饼之间承受更大的麦克斯韦力，从而使铁芯整体振动偏大。绕组在漏磁与电流相互作用下受电磁力而产生振动。由文献[15-17]可知，电抗器铁芯磁致伸缩与电压平方成正比，在铁芯磁场未饱和时，铁芯麦克斯韦力、绕组电磁力与电流平方成正比，即

γ∝k1U2

(1)

Fc.M∝k2I2

(2)

Fw∝k3I2

(3)

式中：γ为磁致伸缩系数；Fc.M为铁芯麦克斯韦力；Fw为绕组电磁力；k1主要与绕组匝数、铁心横截面积、饱和磁感应强度、硅钢片饱和磁通系数有关；k2主要与磁场强度、铁芯表面积有关；k3主要与绕组半径、绕组高度、绕组匝数有关。

电抗器可以等效为电感与电阻串联的设备，因电感远远大于电阻，因此也可以将电抗器简化为纯电感设备，此时绕组电流与电压成正比，即

I∝k4U

(4)

式中：k4主要与电感ωL有关，即k4=1/ωL。

在铁芯磁致伸缩效应、麦克斯韦力与绕组电磁力的作用下，铁芯与绕组产生振动，以加速度表征为

ac∝k5U2

(5)

aw∝k6U2

(6)

式中：k5主要与绕组匝数、铁心横截面积、饱和磁感应强度、硅钢片饱和磁通系数、硅钢片长度、磁场强度有关；k6主要与绕组半径、绕组高度、绕组匝数、绕组质量、垫块和绝缘纸刚度、油的阻尼有关。

基于振动法对电抗器内部机械状态进行分析与诊断，往往通过采集油箱表面的振动信号，因此，油箱表面任意位置处振动为

(7)

式中:kc,i和kw,i分别表示不同位置的铁芯和绕组传递到油箱表面的振动加速度系数，与式(5)、(6)的k5、k6相对应。

由式(7)可知，油箱不同位置处的振动由铁芯和绕组等多种振动源共同耦合叠加产生，由于振动源与振动贡献率的不同，不同测点采集的振动信号也不尽相同。若多相多振动源同时作用，振动在液体路径与固体路径传递过程中会耦合叠加，造成振动加速度与电压平方的线性度关系下降，选取此测点的振动信号对电抗器内部机械故障的分析造成困难。若只有单相振动源单独作用，其振动加速度与电压平方成线性关系，当电抗器内部出现机械故障，此位置相对其他位置，振动信号将更容易出现明显变化，对故障分析更有帮助，因此，可以选择线性度良好的位置为最佳测点。

为充分表示振动加速度与电压平方之间的关系，用最小二乘法对不同电压等级下的振动主频率加速度做线性拟合，并引入R-square描述不同测点振动主频率加速度与电压平方的线性度。

(8)

(9)

(10)

2.2 最佳测点选择

采集图2中72个测点的8个不同电压等级下振动信号，提取傅里叶变换后幅值最大的频率，即振动主频率，如表2所示。通过云图体现不同测点的振动强度分布特征，如图3所示。以曲线反映各测点振动主频率幅值与电压平方的关系，如图4所示(图中，纵坐标g为重力加速度单位，即g=9.8 m/s2)。

表2 不同测点振动主频率Tab.2 Main frequency of vibration at different measuring points Hz

图3 不同测点振动强度分布Fig.3 Distribution of vibration intensity at different measurement points

(a) 第1列

(b) 第2列

(c) 第3列

(d) 第4列

(e) 第5列

(f) 第6列

(g) 第7列

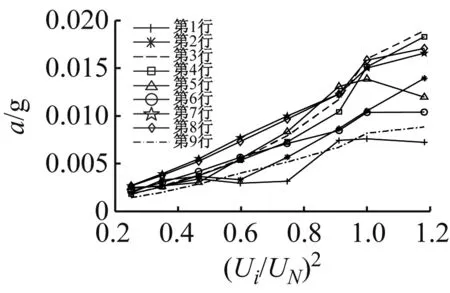
(h) 第8列图4 不同测点振动主频率幅值与电压平方的关系Fig.4 Relationship between amplitude of vibration main frequency and voltage square at different measuring points

由表2可知，不同测点的振动主频率不同，主要以100 Hz、200 Hz、300 Hz为主。进一步分析，电抗器中间部分的振动主频率多为100 Hz，左下区域与右上区域的振动主频率多为200 Hz或300 Hz。根据式(5)、(6)可知，在50 Hz电源作用下，电抗器振动频率为100 Hz，但由于电抗器的模态特性以及多振动源耦合叠加等原因，造成了不同区域的主频率出现差异。按照理论分析，最佳测点的选择应以主频率为100 Hz的区域为主。

由图3可知，在不同电压等级下，电抗器油箱表面振动具有相似的分布特点。振动较大位置多分布于油箱上下两个区域的四个边角，与文献[18]测试的结果一致。其中，左下角、右下角、右上角、左上角四个区域的振动依次呈现增大的趋势，中间区域振动较其他区域相对较小，呈现出“十”字分布特点，这说明各测点振动幅值大小与振动的传播路径有关，大部分振动通过与结构件相连接的顶部和底部固体路径传播，造成振动偏大，而中间区域振动信号直接通过变压器油传播会形成衰减。根据测点选择原理，振动大其相对信噪比较高，能排除内外杂散信号干扰；另一方面，振动过大也会降低对内部轻微机械故障的灵敏度，不利于故障诊断。因此，在振动幅值差距不大的情况，选择振动相对较小的区域作为测点更能灵敏的反映电抗器内部机械故障。

由图4可知，电抗器油箱表面72个测点的振动主频率幅值随电压的增大总体呈现增大趋势。由式(7)可知，电抗器不同位置对应不同振动信号的叠加，加之升压过程中电压等级精准度存在误差等原因，电抗器油箱表面振动主频率幅值与电压平方并不是完全正比关系，出现分段线性特点，与文献[19]分析结果一致。

为具体分析72个测点振动主频率幅值与电压平方之间的线性度关系，应用最小二乘法对曲线拟合，并统计R-square大小，结果如表3所示。

表3 不同测点R-square大小Tab.3 R-square size of different measuring points

由表3可知，R-square大小与振动云图具有相似特点，在电抗器中间“十”字区域R-square数值较大，基本达到0.95以上，部分超过0.99，说明此区域振动主频率幅值与电压平方具有较高的线性度；而四周边角R-square数值较小，线性度相对较弱。因为中间区域多为绕组径向电磁力单独作用，线性度较高，四周边角为多信号源叠加，造成相性度下降。图4展现了部分线性度较高的拟合曲线。

综合振动云图、振动主频率、曲线拟合与R-square大小，最终选择(6,3)、(6,4)、(6,5)、(6,6)为最佳测点。

3 电抗器松动故障检测方法研究

3.1 振动特性分析

按照1.2节电抗器振动试验设置4种机械状态，在第2章选择最佳测点的条件下，挑选线性度更好的(6,3)测点，分析其波形与频谱，如图5所示。

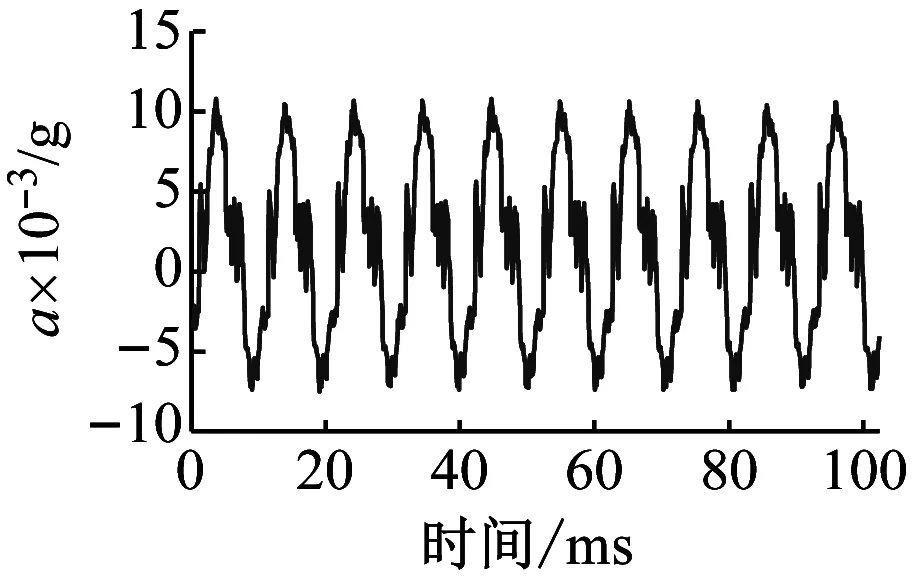
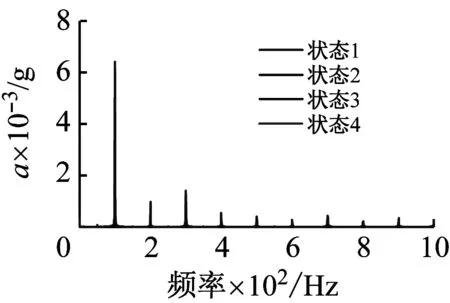
图5 不同状态下测点(6,3)振动波形与频谱Fig.5 Vibration waveform and frequency spectrum of measuring point (6,3) in different states

由图5可知，不同状态下，电抗器振动波形体现出差异，状态2、3、4的波形相差无几，与状态1在波谷相似而波峰有所不同，即从松动开始，电抗器振动信号波形发生变化。

对振动信号进行傅里叶变换，研究其在频谱的变化特点。由图5可知，4种状态下，振动除100 Hz主频率外，还含有大量200 Hz、300 Hz以及其他少量高频成分。仔细分析发现，随着松动程度的增加，100 Hz主频成分逐渐缓慢降低，包括200 Hz、300 Hz在内的高频成分有所增加。

3.2 基于多参量融合的故障检测方法理论研究

在轻微松动故障下，仅从较小变化的振动波形与频谱很难判断电抗器内部机械状态，因此，提出基于多参量融合的电抗器机械故障检测与诊断方法。结合本文研究对象，详细介绍诊断方法原理。

3.2.1 经验模态分解

经验模态分解(empirical mode decomposition, EMD)是一种根据不同时间尺度特征将非线性非平稳信号分解为多个本征模态函数(intrinsic mode functions, IMF)与残差的数据处理方法[20]。对深度挖掘电抗器不同状态之间的有效信息具有极大的帮助， EMD具体步骤如下：

①确定原始振动时域信号x(t)的所有极大值点与极小值点；②应用3次样条插值函数拟合极值点，形成上下包络线，并计算其均值a1(t)；③求得原始信号x(t)与均值的差值d1(t)=x(t)-a1(t)；④判断差值d(t)是否满足IMF要求，若满足，则d1(t)作为第1个IMF，同时记为残差r1(t)=x(t)-d1(t)；若不满足，以d1(t)代替x(t)，重复步骤①～③，直到满足IMF要求；⑤继续分解残差r1(t)，重复以上步骤，直到满足rn(t)为单调函数或其幅值差小于预设值为止[21]。最终将原始振动时域信号x(t)分解为n个IMF与1个残差的和，如公式(11)所示

(11)

式中：x(t)为原始振动时域信号；di(t)为IMF分类；rn(t)为最终残差。

3.2.2 随机森林法

随机森林法(random forest, RF)是以多棵决策树为基础采取多数投票机制的分类器[22]，它是在Bagging重采样与决策树模型的基础上发展起来的。其具体分类路线为：每棵决策树对输入的多参量融合振动特征矩阵产生一个分类结果(标签1、标签2、……)，随机森林算法以投票最多为依据产生最终的决策结果(确定最终分类结果，即标签1、标签2、……)，从而达到更加准确的分类结果。最终分类结果表示如下

(12)

式中：H(x)为随机森林最终分类结果；I(.)为示性函数；hi(x)单棵决策树的分类结果；Y为输出变量。

3.3 基于多参量融合的故障检测方法应用

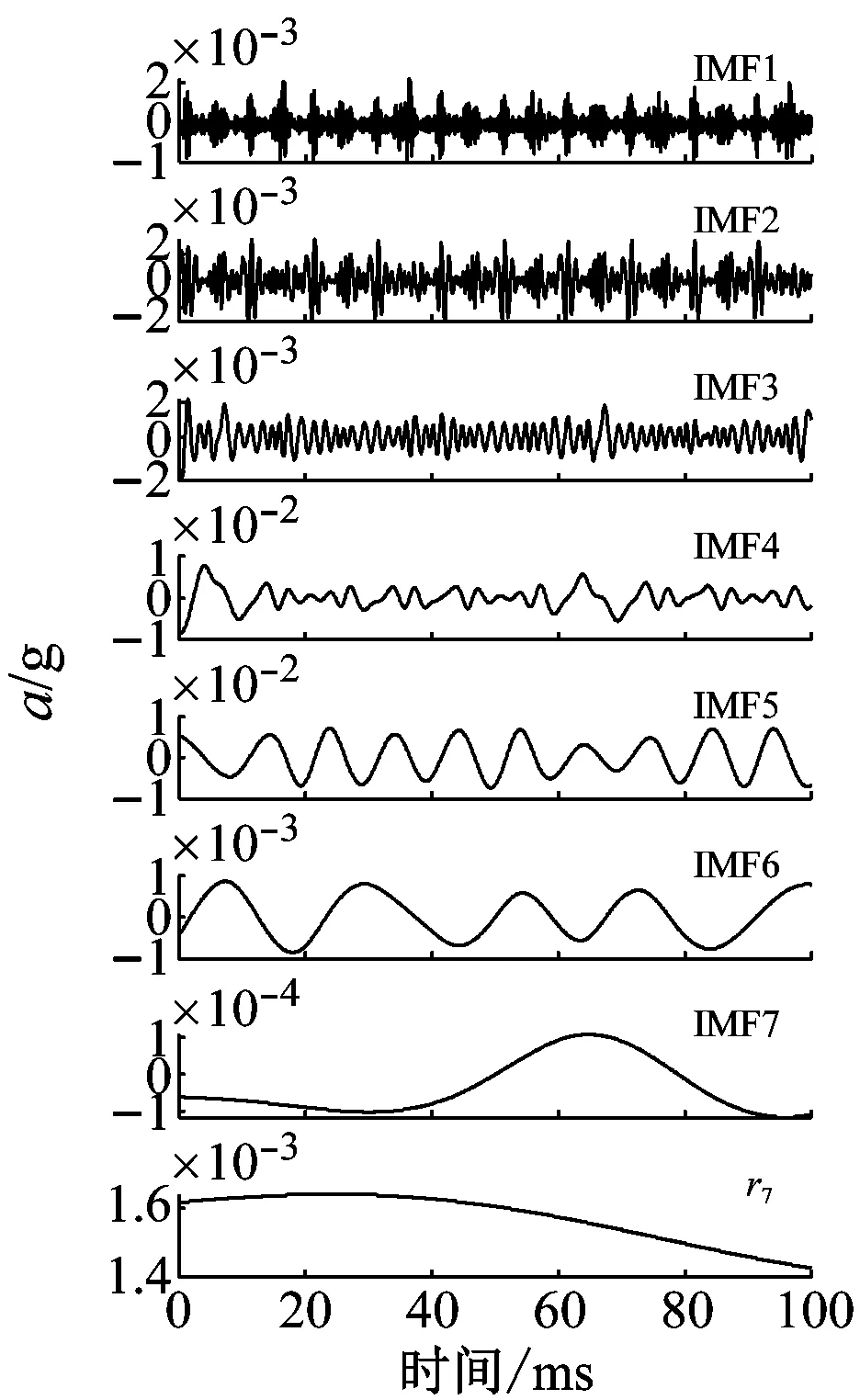
将图5所示的4种状态下的振动波形进行EMD分解，分解结果如图6所示。

由图6可知，EMD将不同状态分解为7个IMF与1个残差，不同模态体现出差异性但差异较小。为进一步提取电抗器不同模态的有效信息，根据模态分解结果重新构建高、中、低频三个模态，即：

(13)

(a) 状态1

(b) 状态2

(c) 状态3

(d) 状态4图6 EMD分解结果Fig.6 Results of EMD

式中：d1、d2、d3分别为重构后高、中、低频模态；t、m、l分别为高、中、低频原始IMF的数量，其数值由过零率确定[23]。

计算高、中、低频模态能量

(14)

计算高、中、低频模态能量占比

(15)

同时，计入欧氏距离L与频谱复杂度H，形成多参量融合的振动特征矩阵[Q1,Q2,Q3,L,H]

(16)

(17)

式中：L为欧式距离；Q′为状态1(正常状态)的能量占比；H为频谱复杂度；pf为频率能量比重。

计算欧式距离时，随机挑选10个状态1的能量占比取平均值Q′；频谱复杂度以50 Hz为步长，频率范围取[50，5 000]Hz。

至此，建立了基于多参量融合的故障检测方法，具体过程如图7所示。根据前述计算测点(6,3)多参量融合的振动特征矩阵，设置随机森林法的分类标签，如表4所示。

图7 多参量融合故障检测方法流程图Fig.7 Flow chart of multi-parameter fusion fault detection method

表4 特征矩阵与分类标签Tab.4 Feature matrix and classification label

由表4可知，不同状态之间的振动特征矩阵出现规律性变化：①通过EMD分解重构的高中低频模态能量占比可以看出，随着松动程度的增加，高频模态能量占比增加，中频模态能量占比减小；②欧式距离随着松动严重程度增加而增加，反映出松动故障后各模态能量占比与正常状态的差异增大；③频谱复杂度随着松动严重程度增加而增加，反映出松动故障后高频模态能量占比增大且振动谐波成分增加、频谱分布复杂化。

通过振动特征矩阵可初步判断电抗器内部机械状态，但难以最终确定，采用随机森林算法对4种不同状态检测与诊断。

随机森林算法中的决策树数量Ktree对最终分类结果有重要影响，若Ktree偏小，计算精度降低，若Ktree偏大，增加计算时间，合适的Ktree可兼顾计算精度与计算时间。对测点(6,3)进行分类且确定最优决策树的数量Ko.tree，以Ko.tree作为决策树数量对测点(6,4)、(6,5)、(6,6)进行分类。图8为测点(6,3)决策树数量Ktree与分类结果正确率关系图，其中，分类正确率定义如下

(18)

式中：n1为验证集分类结果正确数量，n为实际验证集数量。

由图8可知，随着决策树数量Ktree的增加，分类正确率逐渐增大，在Ktree大于90时趋于稳定且在Ktree为100时正确率最大，因此，选择最优决策树数量Ko.tree为100。

图8 决策树数量Ktree与分类结果正确率关系Fig.8 The relationship between the number Ktree of decision trees and the accuracy of classification results

在确定最优决策树数量后，为验证最佳测点选择的正确性以及证明最佳测点分类结果的准确率高，计算测点(6,3)、(6,4)、(6,5)、(6,6)、(1,5)、(4,1)、(7,4)、(9,8)共8个测点的分类结果，如表5所示。

表5 分类结果Tab.5 Classification results

由表5可知：①不同状态的分类结果体现差异，状态1与状态2相对较低，状态3与状态4相对较高，说明在电抗器内部出现松动故障初期，轻微的松动故障与正常状态的特征表现相差无几，出现误判的几率较大，随着松动程度的加大，特征差异越来越明显，判断的正确率显著增加。②挑选的4个最佳测点总分类结果正确率都达到了90%以上，具有较高的应用性与实用价值，其中，测点(6,4)更靠近故障位置，总体正确率高达96.5%，其他测点正确率普遍低于85%，因此，选择最佳测点有助于故障诊断正确率的提高。③对电抗器实施长期振动在线监测，通过基于多参量融合的故障检测与诊断方法，能够反映电抗器内部机械状态。

4 结 论

本文在搭建10 kV高压并联电抗器振动测试平台的基础上，研究了电抗器内部机械故障的振动变化规律，得到以下结论：

(1) 电抗器振动主要以100 Hz为主，还包括大量200 Hz、300 Hz、400 Hz等在内的谐波。

(2) 因传播路径等原因，电抗器油箱表面振动较大区域位于四个边角上；因模态特性、结构和多振动源耦合叠加等原因，不同区域振动主频率不同。

(3) 电抗器油箱中间区域的振动主频率的线性拟合度较高，可以作为最佳测点，从而提高诊断的准确率。本文选择(6,3)、(6,4)、(6,5)、(6,6)为最佳测点。

(4) 提出的基于多参量融合的电抗器机械故障检测与诊断方法对故障具有较高的识别率与判断正确率，可将其应用于电抗器长期振动在线监测，以此反映电抗器内部机械状态。