基于驾驶员心率和速度差的高速公路纵坡度研究*

乔建刚，杨 程，陈彦欣

(1.河北工业大学 土木与交通学院，天津 300401;2.天津市交通工程绿色材料技术研究中心，天津 300401;3.河北省高速公路延崇筹建处，河北 张家口 075400)

0 引言

2020年末，我国高速公路总里程达16.1万km，伴随高速公路总里程逐年增加，交通安全压力持续增大[1]。高速公路交通事故由多因素共同作用导致，其中，人是导致交通事故的主要因素[2-3]。纵坡路段地形复杂且线形变化较大，行车视距受限，行车安全问题严峻[4]。目前，我国高速公路线形设计中，对坡度的限制主要根据汽车的动力性能、道路等级和自然条件等因素，没有考虑驾驶员的心生理特性。

国内外学者围绕驾驶员心率增长率和速度变化对道路行车安全的影响开展大量研究：Jacob等[5]研究行车过程中驾驶员心率与视距和路肩宽度的相关性，并构建回归模型；Antonowicz等[6]指出道路行车安全性在很大程度上取决于驾驶员的心生理状况，并提出通过降低道路对驾驶员心生理影响的方式提升道路行车安全；Kuriyagawa等[7]通过分析得到驾驶员2种心率变化情况，并指出可以通过驾驶员的心率增长率表征道路安全等级；胡立伟等[8]分析上下坡路段、纵坡坡度坡长以及加减速指标对驾驶员的影响，构建驾驶负荷的模型，确定驾驶舒适度的阈值；徐进等[9]基于自然驾驶习惯下的数据，分析公路纵面线形、行车速度和驾驶员心率增长率之间的关系；冯忠祥等[10]通过分析城市下穿隧道纵坡坡度和行车速度与驾驶员心率增长率之间的关系，得到驾驶员心率的变化规律；郭羽熙等[11]运用统计学理论分析驾驶员视觉参数与心率增长率和心率变异性之间的关系。

综上，现有研究多集中分析驾驶员注视特性、心率、驾驶负荷和运行速度与道路参数的相关关系，鲜有作者通过驾驶员心率增长率阈值和运行速度协调性分析纵坡安全坡度。因此，本文选取河北省延崇高速为试验路段，采用心生理检测仪和V-Box采集驾驶员心率数据、道路高程和车辆运行速度数据，研究驾驶员心率和速度差与坡度、坡长之间的关系，并通过心率增长率阈值和运行速度协调性，分析高速公路纵坡路段安全坡度，研究结果可为高速公路交通安全和人性化设计提供理论依据。

1 基本理论及试验设计

1.1 心生理理论

驾驶员在行车过程中，实时心率会随行车时间和行驶路程的增加而不断变化，呈现出类似随机信号的现象。将试验测得随时间变化的驾驶员心率当做随机信号序列[12]，表达函数为x(i)(i=1，2，…，N-1)。其均值函数如式(1)所示：

(1)

式中：i为驾驶员心率随机信号序号；μx(i)为均值函数；x(i)为试验采集到的驾驶员心率随机信号；N为自然数，取0，1，2，…。

自相关函数如式(2)所示：

(2)

式中：r(i，i+m)为随机信号的自相关函数；m为心率信号的延迟间隔，m=0，1，…，N-m-1。

驾驶员行车心率变化情况可通过时域中的相关函数分析，如式(3)所示：

(3)

通过离散的傅里叶变换，把时域图上的心率信号转化为频率上的心率信号。设随机信号序列函数为X(i)(i=1，2，…，N-1)，傅里叶变换如式(4)所示：

(4)

式中：X(z)为x(i)的像函数；z为单位Z变化复变量；j为虚单位；w为圆频率，w=2πf，其中f为频率。

通过式(4)可得到功率谱密度的估值如式(5)所示：

(5)

式中：PN(z)为功率谱密度函数。

运用式(4)～(5)通过信号转换可以得到驾驶员行车过程中的心率功率谱图。功率谱图能够量化分析行车过程中因道路线形、交通环境和行车视距等因素影响以及驾驶员心生理变化情况。

选用心率增长率作为驾驶员心生理状态的指标，心率增长率能够反映行车过程中驾驶员心率变化幅度，进而反映道路线形对驾驶员心理反应影响[13]，如式(6)所示：

(6)

式中：N为驾驶员心率增长率，%；n1为驾驶员心生理状态平静时的心率均值，次/min；n2为驾驶员的动态心率，次/min。

乔建刚[14]研究得到驾驶员舒适、紧张和恐惧的心率增长率阈值分别为18%，27%，39%，以此作为驾驶员心生理状态的评价标准，当心率增长率超过27%时，驾驶员处于紧张驾驶状态，驾驶操作失误增多，容易产生交通事故。

1.2 速度协调性

《公路项目安全性评价规范》(JTG B05—2015)[15]采用运行速度的差值，对路段的运行速度协调性进行评价，评价标准见表1。

表1 速度差评价标准Table 1 Evaluation criteria of speed difference km/h

1.3 试验路段

选取河北省延崇高速公路为研究对象，试验路段为双向4车道，设计车速为100 km/h，多纵坡且平曲线半径大于1 km，视距充足，符合纵坡路段安全分析试验要求。为排除不良天气影响，试验天气晴朗，光线充足，试验时段为8∶00-18∶00。

1.4 试验人员

选取26名驾驶员进行实车试验，被试人员年龄在26～40岁之间，均取得C1以上驾照且驾驶技术熟练；试验前均进行过仪器使用培训，身体健康，试验前心生理状态良好。

1.5 试验设备

试验采用KF2型动态多参数生理检测仪、V-Box数据采集仪和五轮仪。KF2型动态多参数生理检测仪实时记录驾驶员的心电图、心率变化，工作时间大于24 h；V-Box用来记录车辆的行驶速度、距离以及道路的高程变化，速度采集精度0.2 km/h，距离采集精度0.05%；五轮仪用来记录试验车辆的加速度变化。试验车辆为大众小型汽车，驾驶员均驾驶同一辆车，避免车辆差异导致试验误差。

2 数据分析

2.1 偏相关分析

为确定高速公路纵坡路段行车时影响驾驶员心率增长率和行车速度差的显著性因素，对驾驶员心率增长率和速度差分别与纵坡坡度、坡长进行偏相关分析，见表2～3。

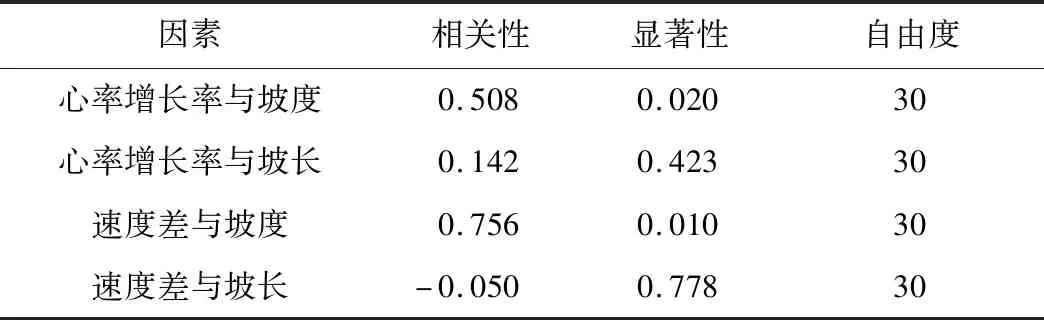
表2 上坡路段偏相关分析Table 2 Partial correlation analysis of uphill road section

由表2可知，在上坡路段行驶时，驾驶员心率增长率与坡度的偏相关系数为0.508，双侧显著性概率p=0.020<0.05，因此心率增长率与坡度显著相关；心率增长率与坡长的偏相关系数为0.142，双侧显著性概率p=0.423>0.05，因此心率增长率与坡长弱相关性。同理得到速度差与坡度呈显著相关，与坡长呈弱相关，相关系数分别为0.756和-0.050。

由表3可知，在下坡路段行驶时，驾驶员心率增长率与坡度的偏相关系数为-0.574，双侧显著性概率p=0.003<0.05，因此心率增长率与坡度显著相关；心率增长率与坡长的偏相关系数为-0.126，双侧显著性概率p=0.465>0.05，因此心率增长率与坡长弱相关性。同理得到速度差与坡度显著相关，与坡长弱相关，相关系数分别为-0.690和0.078。综上，在纵坡路段行车时，坡度与心率增长率和速度差呈显著相关，坡长与心率增长率和速度差呈弱相关。

表3 下坡路段偏相关分析Table 3 Partial correlation analysis of downhill road section

2.2 上坡路段安全性分析

1)心率增长率与坡度关系

对上坡路段驾驶员的心率增长率与坡度进行分析，如图1所示，图中平行x轴虚线对应驾驶员紧张阈值27%。通过SPSS软件对上坡心率增长率与坡度进行分析，得到式(7)：

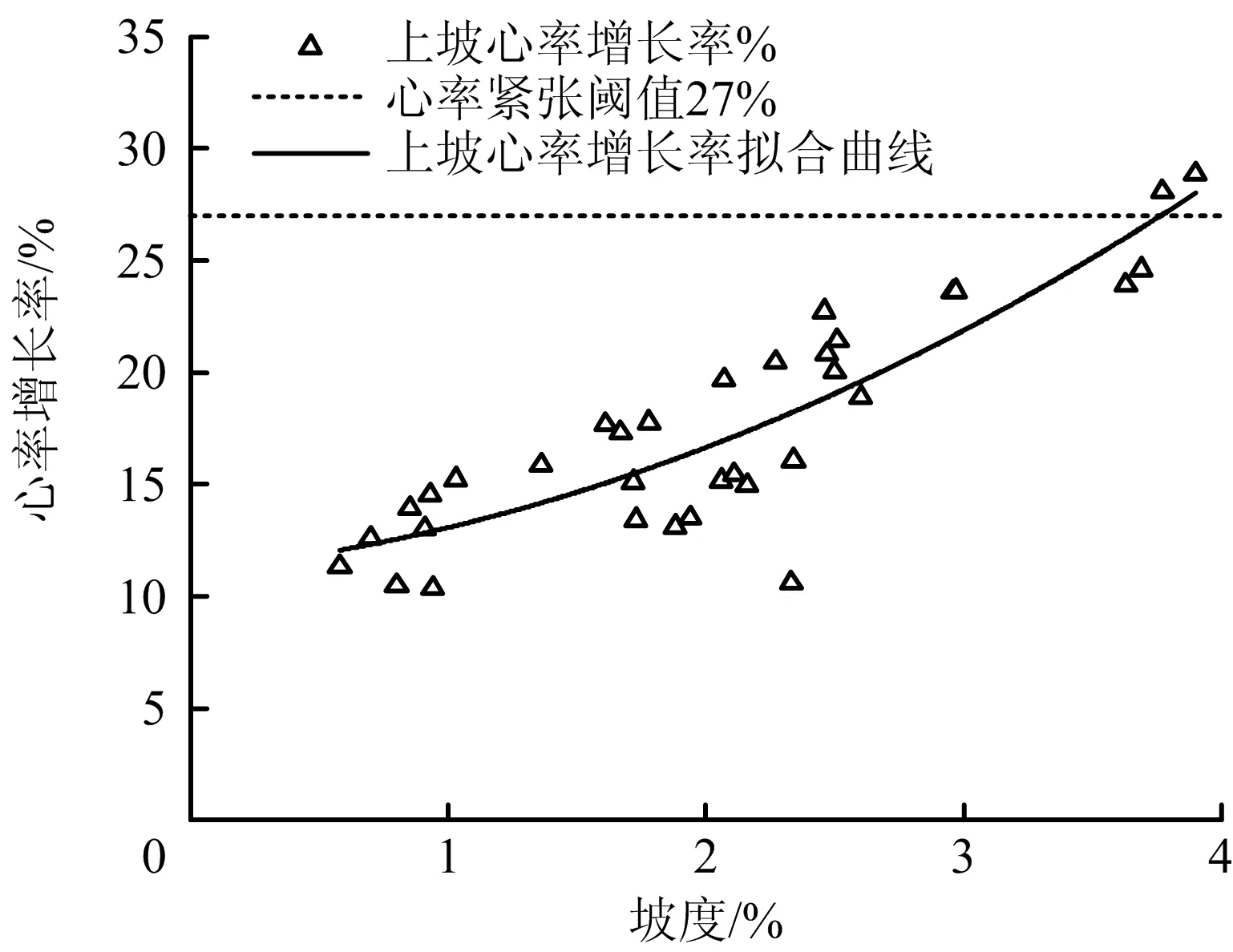
图1 上坡心率增长率与坡度关系Fig.1 Relationship between growth rate of heart rate and slope of uphill road section

N1=82.887i12+1.088i1+0.112

(7)

式中：N1为与上坡坡度相关的驾驶员的心率增长率，%；i1为上坡坡度，%。R2=0.751，F0.05=50.817，模型通过相关性检验。

由图1和式(7)可知，当驾驶员在上坡路段行驶时，随纵坡坡度增大，心率增长率逐渐增大，整体呈正相关。当i1=3.7%时N1=26.5%，i1=3.8%时N2=27.3%，因此当坡度大于3.7%后，驾驶员心率增长率超过紧张阈值27%，开始紧张驾驶。

2)速度差与坡度关系

选取坡底、坡中和坡顶的速度，对上坡路段连续行驶速度与坡度进行分析，如图2所示。

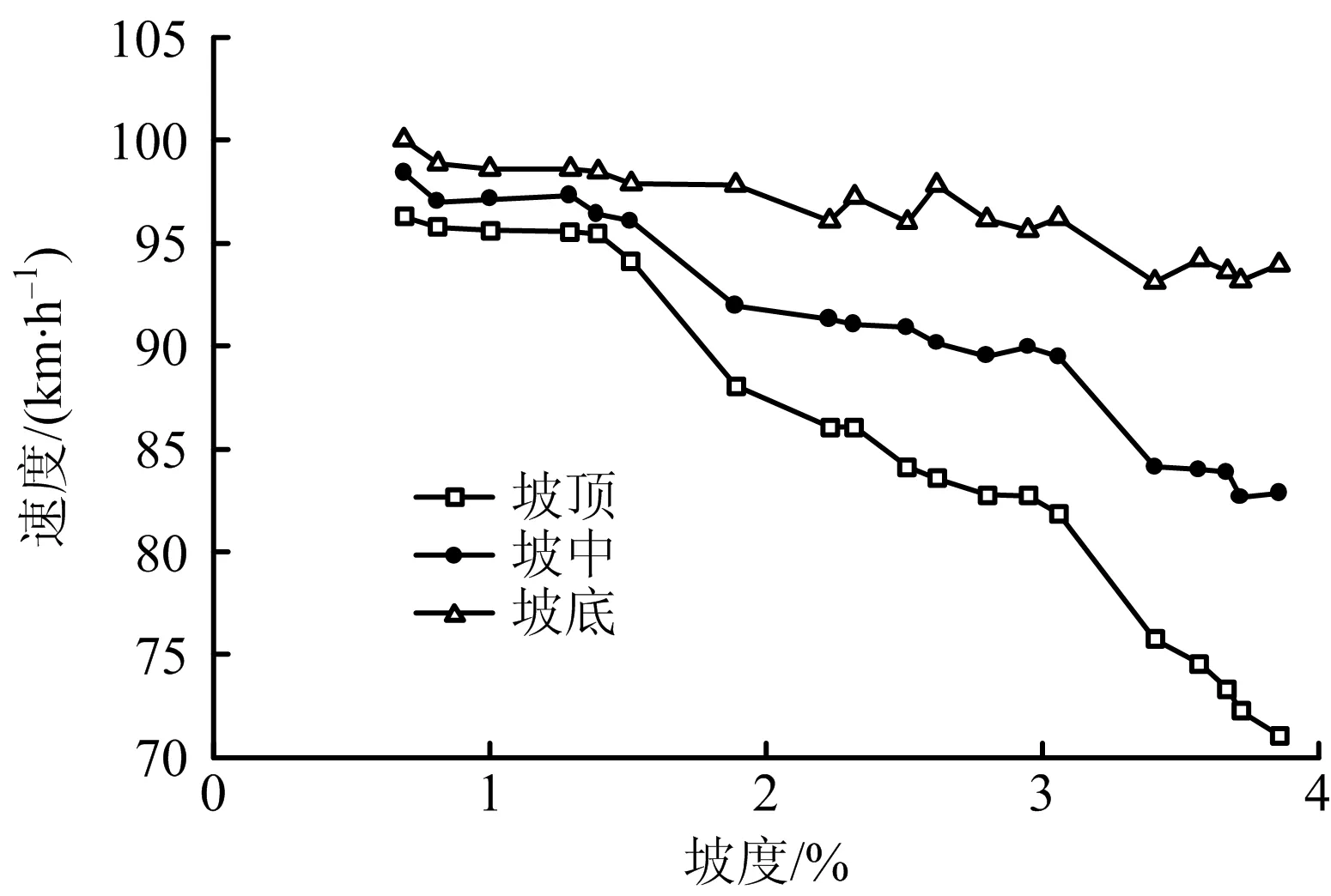
图2 上坡不同位置速度分析Fig.2 Speed analysis of different positions on uphill

由图2可知，当坡度小于1.5%时，随坡度升高，驾驶员速度变化较小，稳定在95～100 km/h之间；当坡度大于1.5%后，随坡度增加，速度整体呈下降趋势。上坡行驶是减速过程，坡底速度最高，坡顶速度最低。选取坡顶与坡底速度的差值与坡度进行相关性分析，如图3所示，图中平行x轴虚线对应运行速度协调性不良的阈值20 km/h。

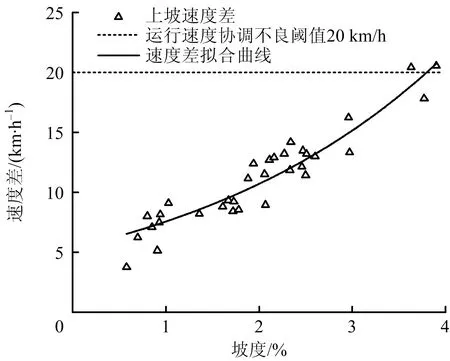
图3 上坡速度差与坡度关系Fig.3 Relationship between speed difference and slope of uphill road section

通过SPSS软件对上坡速度差与坡度进行分析得到式(8)：

ΔV1=5.346·e34.718i1

(8)

式中：ΔV1为与上坡坡度相关的速度差，km/h；i1为上坡坡度，%。R2=0.897，F0.05=1 422.588，模型通过相关性检验。

由图3和式(8)可知，随坡度增大，速度差逐渐增大，整体呈正相关。当i1=3.8%时，ΔV1=19.9 km/h，i1=3.9%时，ΔV1=20.7 km/h，因此当坡度大于3.8%后，车辆的速度差超过20 km/h，运行速度协调性不良。

综上，当坡度不大于3.7%时，驾驶员的心生理状态良好，当坡度不大于3.8%时，运行速度协调性较好，因此建议上坡路段坡度不大于3.7%。

2.3 下坡路段安全性分析

1)心率增长率与坡度的关系

对下坡路段驾驶员心率增长率和坡度进行分析，如图4所示，图中平行x轴虚线对应与驾驶员心率增长率紧张阈值27%。

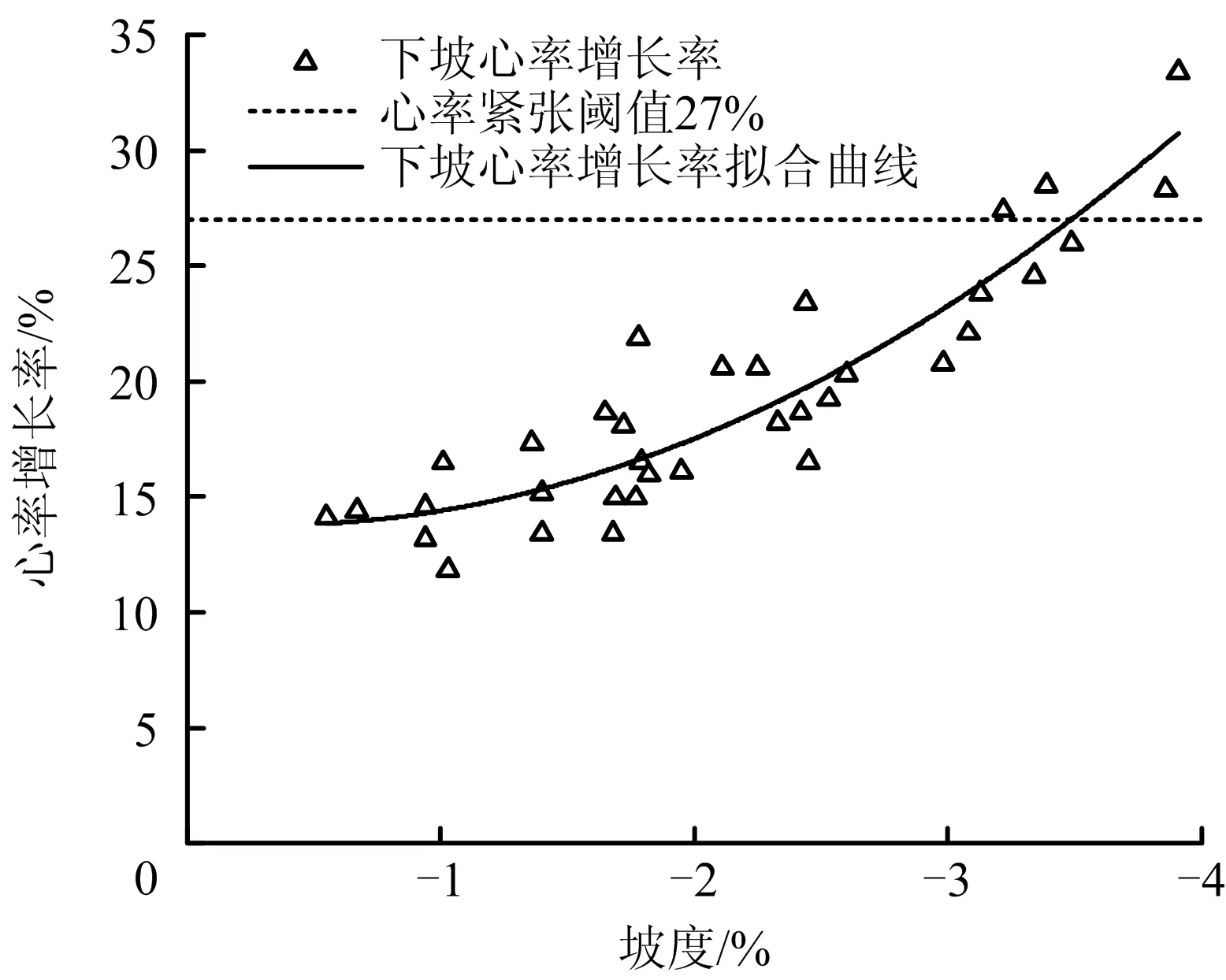
图4 下坡心率增长率与坡度关系Fig.4 Relationship between growth rate of heart rate and slope of downhill road section

通过SPSS软件对下坡路段心率增长率与坡度进行分析得到式(9)：

N2=130.619i22+0.793i2+0.139

(9)

式中：N2为与下坡坡度相关的驾驶员心率增长率，%；i2为下坡坡度，%。R2=0.837，F0.05=91.059，模型通过相关性检验。

由图4和式(9)可知，下坡路段随坡度增加，驾驶员心率增长逐渐增大，整体呈正相关。当坡度小于2%时增幅较缓，当坡度大于2%后增幅逐渐变大。当i2=3.4%时N2=26.3%，i2=3.5%时N2=27.1%，因此当坡度大于3.4%后，驾驶员心率增长率超过紧张阈值27%，开始紧张驾驶。通过对上、下坡驾驶员心率增长率分布进行分析发现，下坡路段心率增长率分布超过紧张阈值的相对较多，因此下坡路段驾驶员更易产生紧张驾驶，应重点防控。

2)速度差与坡度关系

同理对下坡路段连续行驶速度与坡度进行分析，如图5所示。

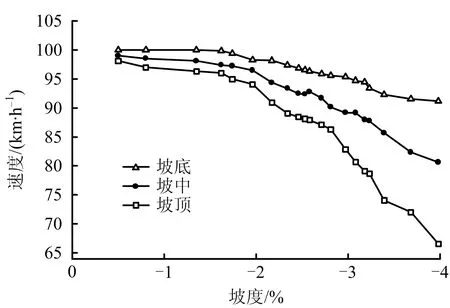
图5 下坡不同位置速度分析Fig.5 Speed analysis of different positions on downhill

由图5可知，当坡度小于1.7%时，随坡度增加，速度变化不大，稳定95～100 km/h之间；当坡度大于1.7%后，随坡度增加，速度整体呈下降趋势。由于车辆重力在纵坡行驶方向分力的作用，下坡是加速过程，坡顶速度相对最低，坡底速度相对最高。选取坡顶和坡底速度的差值与坡度进行相关性析，如图6所示，图中平行x轴虚线对应运行速度协调性不良的阈值20 km/h。

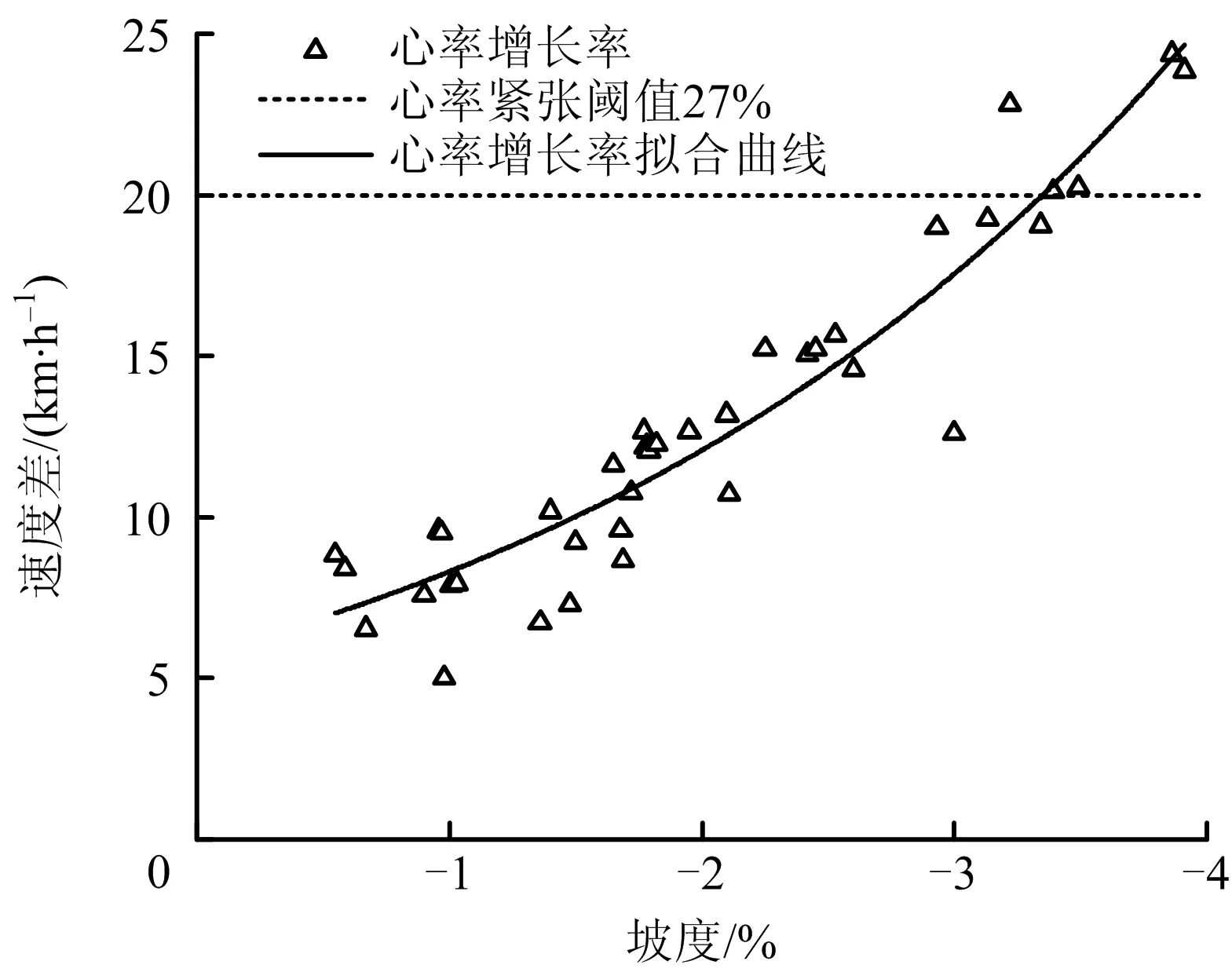
图6 下坡速度差与坡度关系Fig.6 Relationship between speed difference and slope of downhill road section

通过SPSS软件对下坡路段速度差与坡度进行分析得到式(10)：

ΔV2=5.716·e-37.422i2

(10)

式中：ΔV2为与下坡坡度相关的速度差，km/h；i2为下坡坡度，%。R2=0.889，F0.05=1 229.535，模型通过相关性检验。

由图6和式(10)可知，随坡度增大，速度差逐渐上升，整体呈正相关。当i2=3.3%时，ΔV2=19.6 km/h，i2=3.4%时，ΔV2=20.4 km/h。因此当坡度大于3.3%后，车辆的速度差超过20 km/h，运行速度协调性不良。

综上，当坡度小于等于3.4%时，驾驶员心生理状态良好，当坡度小于等于3.3%时，运行速度协调性较好，因此建议下坡坡度应小于等于3.3%。

2.4 安全坡度确定

综合考虑驾驶员心生理状态和运行速度协调性，高速公路上、下坡安全坡度范围如表4所示。

表4 安全坡度范围Table 4 Range of safe slope

考虑到高速公路双向的整体性及规范的统一性，纵坡路段的最大坡度Imax取值如式(11)所示：

Imax=min{i1，i2}=3.3%

(11)

因此，建议设计车速100 km/h的高速纵坡坡度应小于等于3.3%，以提升驾驶舒适性，保证高速行车安全。

3 结论

1)通过偏相关分析，确定纵坡路段影响驾驶员心率增长率和行车速度差的显著性因素，分别构建驾驶员心率和速度差与坡度之间的关系模型。

2)上坡路段，当坡度小于等于3.7%时，驾驶员心率增长率小于紧张阈值27%且行车速度差小于20 km/h，驾驶员心生理状态良好，运行速度协调性较好，对驾驶员影响较小；下坡路段，当坡度小于等于3.3%时，驾驶员心率增长率小于紧张阈值27%且行车速度差小于20 km/h，驾驶员心生理状态良好，运行速度协调性较好，对驾驶员影响较小。因此建议设计车速100 km/h的高速公路纵坡坡度应不大于3.3%。