永磁同步电机多参数自适应补偿弱磁控制策略

项柏潭，梅三冠，时 帅

(江南大学 物联网工程学院, 无锡 214122)

0 引 言

由于具有功率密度高、可靠性强、高效率等特点，永磁同步电机(以下简称PMSM)在电动汽车等调速范围要求较广的驱动系统中得到了广泛的应用[1]。当电机工作在弱磁区域内时，需要保证电机的转矩可以精确地跟随给定。然而，电机参数受运行时的温度、定子绕组电流和磁通饱和度等因素的影响[2]，当电机长时间高速运行时，其实际参数与控制方法中不一致，影响电机稳定运行时的转矩控制精度，导致电机的控制性能下降[3]。因此，在电机驱动控制系统中，需要实时准确地获取电机的实际参数[4-5]，以提高电机的输出转矩精度和控制性能。

针对电机参数变化引起控制性能下降的问题，目前主要有以下三类解决思路：(1)将电机参数辨识算法和弱磁控制算法相结合，把辨识得到的参数实时反馈到弱磁控制算法中，达到改善电机控制性能的目的[6]；(2)将前馈控制引入到弱磁控制算法中，降低算法对电机参数的敏感性[7]；(3)预先估计参数变化引起的误差，然后将其补偿到弱磁控制算法中[8]。上述三类方法中，第一类可以更好地提高电机在参数发生变化后的控制性能，通过选用合适的算法，可以实现对PMSM多个电气参数同时准确识别，进而对其进行补偿。

目前的参数辨识研究中，需要辨识的PMSM参数主要有交直轴电感和永磁体磁链。常用的方法包括离线参数辨识和在线参数辨识两大类。离线参数辨识的方法主要有查表法[9]，其通常仅针对一个参数进行辨识，且依赖于大量实验数据建表，可移植性较差，并且不能实时对电机的参数进行辨识。而在线参数辨识方法实现了对参数的实时跟踪，主要有以下几种方法：最小二乘法[10]、卡尔曼滤波算法[11]、模型参考自适应算法[12]等。最小二乘法具有简单和易实现等优点，但需处理大量数据，存在数据易饱和的问题，且在非稳态条件下，跟踪能力较差。卡尔曼滤波算法通过将部分参数设为固定值，从而实现对其它参数的辨识，但卡尔曼滤波算法的设计比较复杂，并且对噪声的鲁棒性较差，由于被设为固定值的参数实际仍会发生变化，所以稳态误差较大。在模型参考自适应算法中，待辨识参数识别的准确率和快速性与算法中使用的参数具有较强的相关性，参数的选取会直接影响最终的辨识效果。

为了实现多个参数同时补偿，文献[3]提出了一种弱磁区域参数补偿策略，其中的弱磁控制方法使用文献[12]中提出的基于单q轴电流调节器的电压矢量角弱磁控制策略(Single Q-axis Current Regulator-Variable Voltage Angle, SQCR-VVA)，其优点是在保证电流动态性能的同时解决了两个电流调节器的调节冲突与饱和问题。上述参数补偿方法可以实现多个参数的同时补偿，且具有良好的抗扰性能，但该方法在建立参数补偿模型时，忽略了定子电阻上压降的影响，并且引入多个新的参数，使得输出转矩的稳态误差较大。

在此基础上，本文设计了一种PMSM多参数自适应补偿算法，通过分析在弱磁区域由于参数变化引起的电流和电压误差，建立参数补偿模型，简化了补偿方法，改善了输出转矩误差较大的问题，提高了电机在参数发生变化后的控制性能。最后通过实验验证方法的可行性。

1 参数敏感性分析

1.1 PMSM数学模型

在同步旋转参考坐标系下，PMSM的稳态电压方程：

(1)

式中：Rs为定子等效电阻；Uq和Ud分别是定子电压的交、直轴分量；iq和id分别是定子电流的交、直轴分量；Lq和Ld分别是定子等效电感的交、直轴分量；ωs是同步角速度；ψf是永磁体磁链。

转矩方程：

(2)

式中：Te是电磁转矩；p是极对数。从转矩方程中不难看出，转矩受Ld、Lq和ψf的影响。

(3)

(4)

式中：us是电压幅值，is是电流幅值。

当PMSM工作在基速区间内时，为保证电机的定子电流最小，以使得如铜耗等损耗最小，采用最大转矩电流比控制策略，直轴电流分量如下：

(5)

当电机工作在弱磁区域时，电机的电压饱和，即us=umax。定义电压矢量角θ为us与d轴之间的夹角，则当电机工作在电动状态下时，π/2<θ<π。电机的交直轴电压分量如下：

(6)

1.2 参数误差分析

当PMSM工作在弱磁区域时，电压矢量角θ是唯一的可调节量，可以通过调节θ达到控制电机的目的。同时，为了更好地规划电流轨迹并提高电流动态性能，可以增加一个电流调节器。而为了简化分析电流、电压误差和参数变化系数之间的关系，本文采用的弱磁控制方法为SQCR-VVA，其控制框图如图1所示。

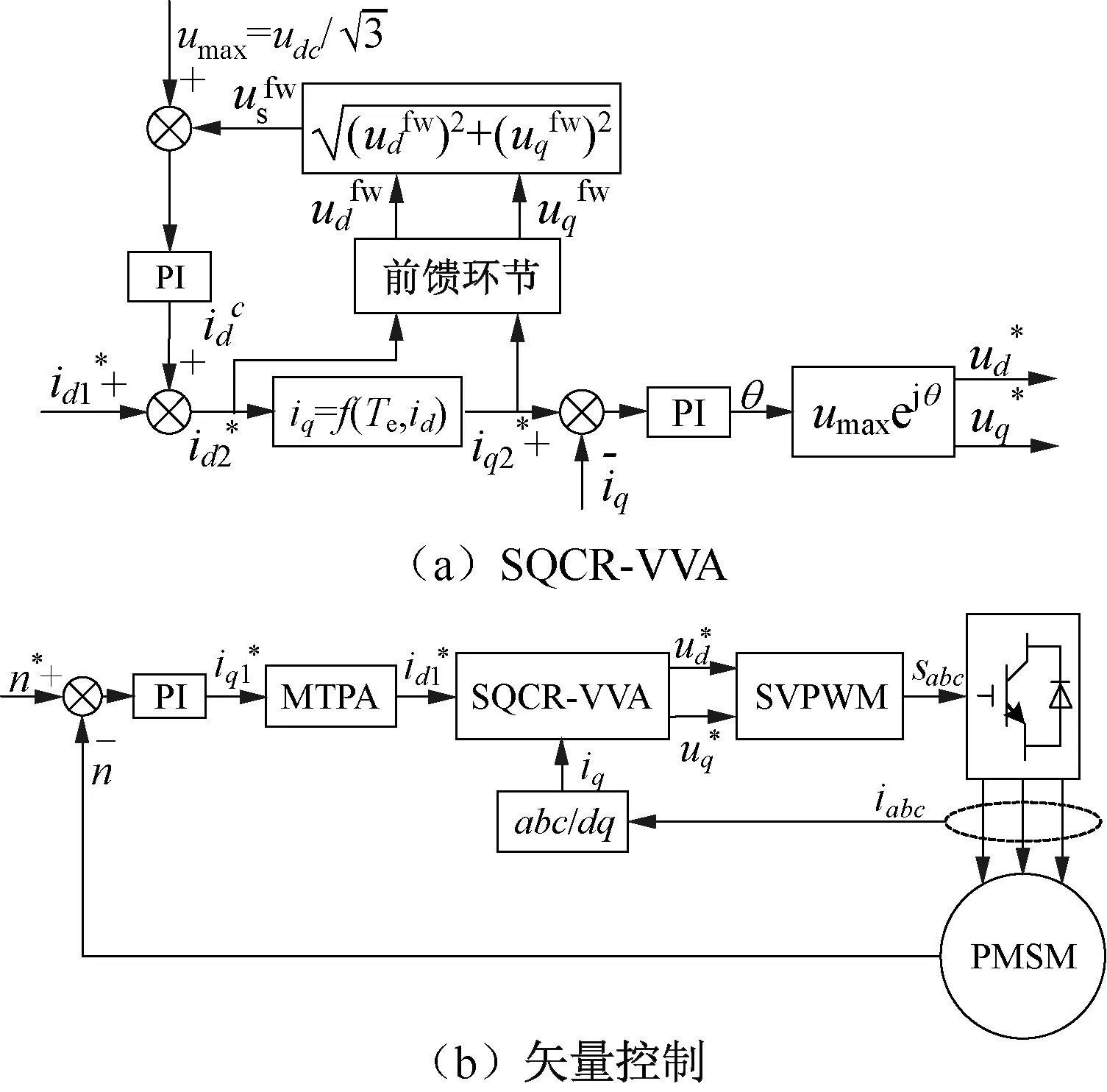
图1 SQCR-VVA弱磁控制框图

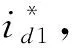
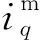
(7)

(8)

(9)

在参数发生的变化瞬间，电流和转速(ωs)均不会发生变化，由式(1)可知：

(10)

2 参数误差补偿

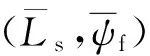
(11)

(12)

式中：α是定子电感的变化系数；β是永磁体磁链的变化系数，受温度、电流和磁通饱和度等的影响，其变化范围是[5]：

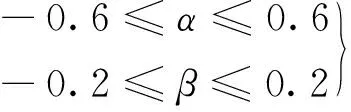
(13)

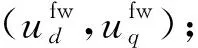
(14)

对本文中所用的隐极式电机，考虑定子电感Ls和永磁体磁链ψf对电机控制精度的影响，分为三种情况进行讨论。

2.1 单参数补偿

2.1.1 定子电感

当只有定子电感Ls的值发生变化时，据式(1)、式(7)、式(11)、式(12)，有：

(15)

(16)

(17)

通过式(17)可以计算出定子电感Ls的变化系数，进而对电感的偏差进行补偿。

2.1.2 永磁体磁链

当只有永磁体磁链ψf的值发生变化时(α=0)，式(16)中A=RΔid，据式(14)、式(16)有：

(18)

(19)

通过式(19)可以计算出永磁体磁链ψf的变化系数，进而可以对永磁体磁链的偏差进行补偿。

2.2 多参数补偿

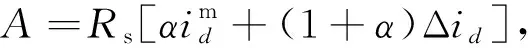
基于上述分析，可以在电机参数发生变化时，检测到参数变化的大小，然后对参数进行补偿，使电机的输出转矩始终跟随给定并工作在最优电流曲线上。带参数补偿的SQCR-VVA控制框图如图2所示。

图2 带参数补偿的SQCR-VVA控制框图

(20)

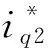
3 实验验证与结果分析

为了验证本文提出的参数补偿算法在实际电机驱动控制系统中的性能，搭建0.75 kW的PMSM驱动系统实验平台如图3所示，使用的PMSM参数如表1所示。

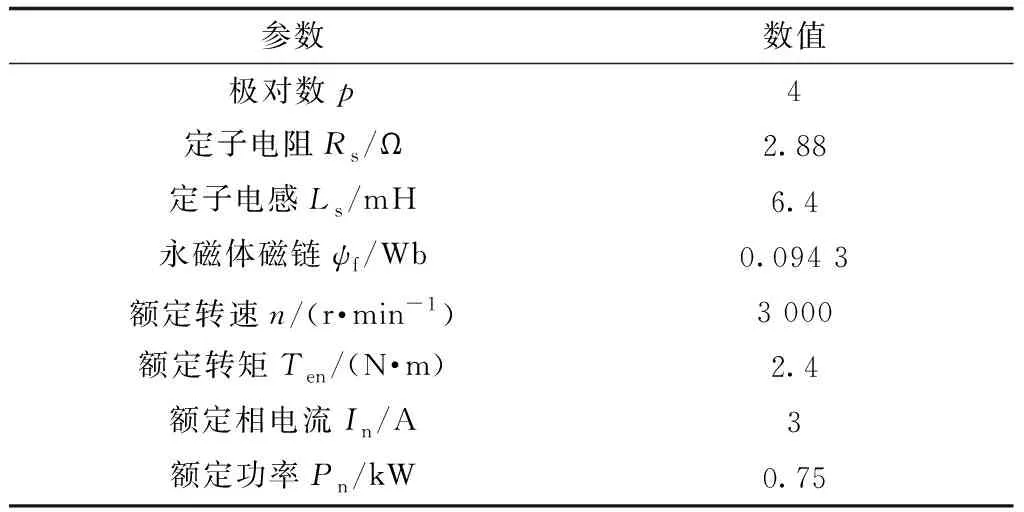
表1 PMSM参数

图3 0.75 kW PMSM驱动系统实验平台

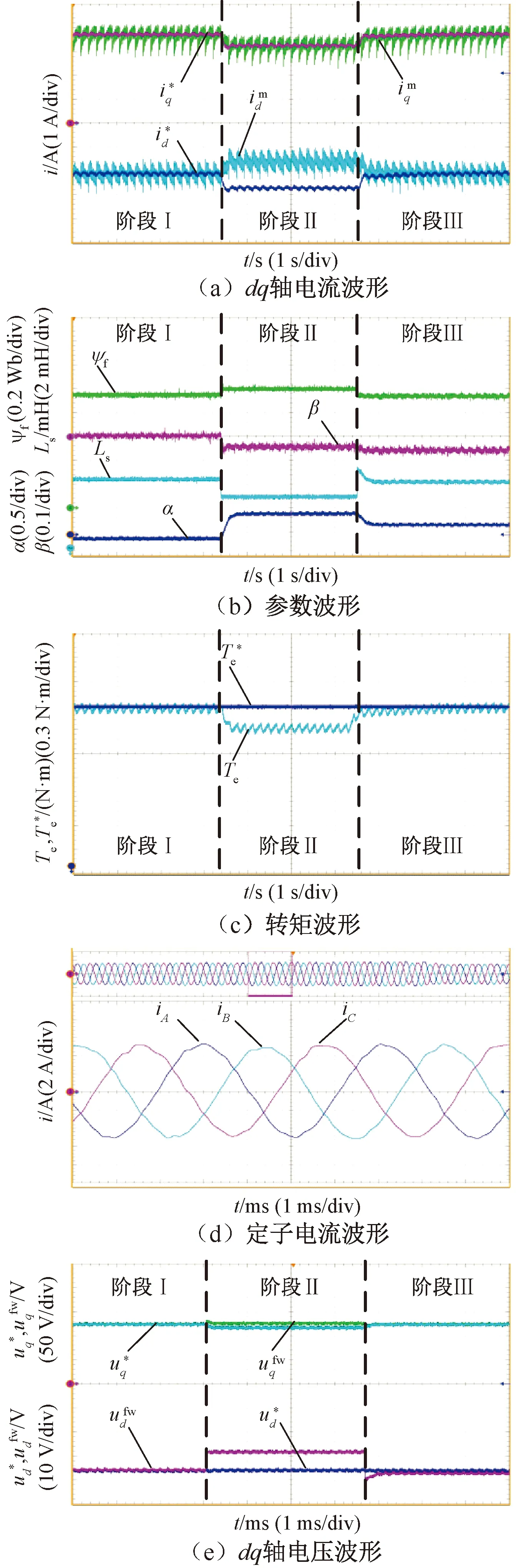
图4 α=1.3, β=-0.05时的实验结果

从图4中可以看出，当电机两个参数同时发生变化时，多参数自适应补偿算法可以有效地补偿由两个参数同时变化引起的电流和转矩误差。在阶段Ⅲ中切入参数补偿算法后，可以使系统重新恢复到参数未发生变化的工作状态。为了证明此状态下控制系统也有较好的转矩控制性能，多次重复实验，分别取阶段Ⅱ中间1 s和阶段Ⅲ最后1 s的转矩平均值计算得到：在阶段Ⅱ转矩下降了12.02%，在阶段Ⅲ转矩误差为0.38%。

综上所述，多参数自适应补偿算法在实际电机控制系统的参数发生变化时，可以有效地抑制参数变化对系统输出的影响，提高在参数发生变化后的转矩控制精度，显著改善电机的控制性能。文献[3]中所用方法在多个参数同时变化时，输出转矩的误差在5%的范围内。本文中所用的方法则可以使转矩误差小于1%，更好地提高了在参数变化时的转矩控制精度。

4 结 语

本文提出的多参数自适应补偿算法具有结构简单、易实现等优点，在电机处于弱磁控制阶段，定子电感和永磁体磁链发生变化时，可以通过电流和电压误差准确地辨识出多参数变化，并反馈到控制算法中，进而改善由于参数变化导致的输出转矩无法跟随给定的问题。算法的参数辨识误差在5%以内，实际输出转矩的平均值与期望转矩间的误差小于1%，实验验证了算法的准确性和有效性。