U型过江管道沉放施工过程动力响应分析

肖扬洋 巫志文 潘明煌 吴昌松 方一如

摘要：U型管道沉放施工过程涉及多体耦合、结构形状不规则、吊缆下放协调难等问题。为了保证施工安全和精度，基于水动力分析软件OrcaFlex，建立了U型过江管道沉放系统沉放过程中的数值分析模型，研究了典型工况下吊缆和锚索的张力、管道的动力响应和沿其长度方向的应力分布、钢浮筒的动力响应，并对吊缆张力进行了关键参数敏感性讨论。结果表明：沉放过程是安全可靠的，但是操作不当极易造成吊缆张力过大;实际工程中建议采用先管道两边后中间的气囊消气方式，气囊消气时间和吊缆下放速度需相互协调，中间吊缆的下放速度或初始下放时刻稍慢于两边;同时有必要对各吊缆张力和管体的运动姿态进行实时监测。研究可为实际沉放施工和其它类似工程提供参考依据。

关 键 词：U型管道; 沉管施工; 多体耦合; 吊缆下放; 沉放系统; 动力响应; OrcaFlex

中图法分类号： TU991.36

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.05.032

0 引 言

沉管法[1]是将若干个预制管段分别浮运到海面（江面）现场，通过注水、吊缆下放等方式将管段从水面逐个沉放至水下基槽内，以此完成水下结构修建的施工方法。由于其具有总工程量小、工期短、工程造价低、可以交叉作业缩短工期等优点而被广泛使用[2]。但是，沉管施工过程通常涉及管段形状长大钝体、管段和波流流固耦合、管段与缆索耦合等问题[3]，给施工质量和安全带来了极大不确定性。

为准确把控管段沉放过程的受力、运动和平稳性，确保沉放施工的安全，国内外学者对管段结构在沉放过程中的动力响应进行了广泛研究。Chen等[4-5]建立沉管管段沉放的频域和时域数学分析模型，研究了沉管管段在不同海况下的动力响应。梁邦炎[6]等基于相似理论和相对运动概念，在拖曳水池完成了沉管管段沉放过程的水动力学试验，研究了沉管管节在不同风浪流载荷组合作用下的管节受力和运动响应。吕卫清等[7]以港珠澳大桥为工程背景，通过水池试验模拟了大尺度沉管比例模型的管节沉放等待和沉放过程，得到了沉管系泊状态下水动力特性的一般规律。Huang等[8]通过物理模型试验研究了随机波浪对沉管管段沉放运动特性的影响，结果表明，沉管管段对消除干舷阶段的动力响应最为强烈。Song等[9]通过沉管管段沉放的物理模型试验，分析了沉管管段在随机波浪作用下的运动响应以及控制缆绳受力情况。杨璨等[10-12]开展双驳船与沉管管节耦合的沉放物理模型试验与数值模拟，对不同波浪要素条件下沉管管段的运动特性进行了研究。

然而，上述沉管管段大部分为规则直线型，

在某些特殊情况下，比如由于河床等条件的限制，需将过江管道做成不规则的形状，其受力机理相比于直线规则形状的沉管管段要复杂很多。更为特殊的是，相比于海洋大型结构的沉放施工，过江管道由于江面施工空间和上游通航的限制，难以使用水上大型沉吊设备，通常需要为其配置数量繁多的钢浮筒、气囊、驳船、履带吊等辅助其沉放施工。同时在过江管道沉放过程中，因涉及到浮力转移的均匀性、吊缆下放的协调性、多体耦合等方面的问题，控制不当，极易发生缆索断裂等事故。因此，有必要对该复杂构型过江管道沉放过程进行深入研究，保证施工安全。

本文以广西右江过江管道沉放工程为工程背景，基于OrcaFlex水动力分析软件，建立U型过江管道沉放系统在沉放过程中的数值模型。研究了典型工况下吊缆和锚索的张力、管道的动力响应和应力分布、钢浮筒的动力响应，并对吊缆张力进行关键参数敏感性讨论，可为实际工程的施工提供参考依据。

1 工程概况

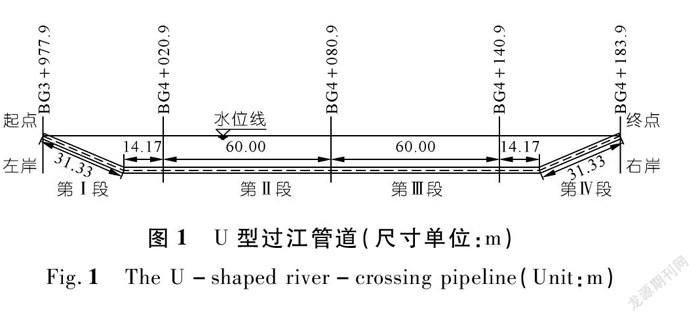
本文综合考虑河床形态、通航、管道制作后的吊装、下水方式等因素，将过江管道长度设计为211 m，共分成4段焊接而成，管道整体呈现“U”字形，如图1所示。

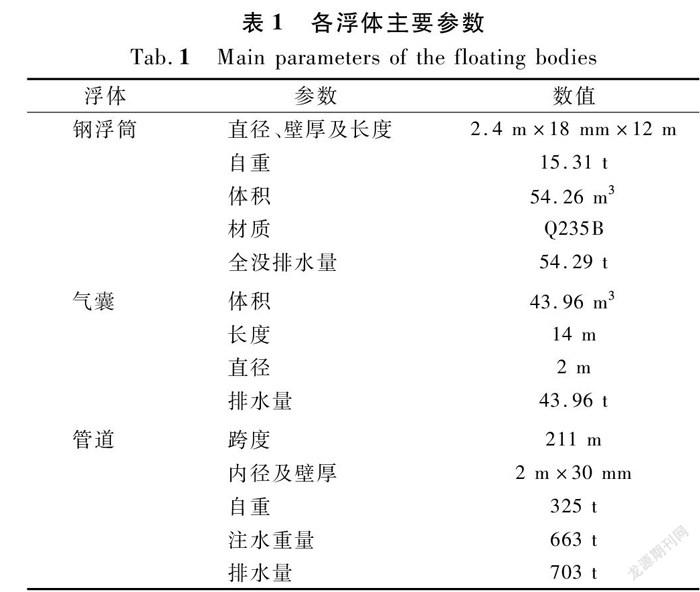
图2为整管的沉放系统布置图，包括一根“U”字形过江管道、6艘起吊能力为20 t（约为196 kN）的浮吊船、2台起吊能力为100 t的履带吊、5个钢浮筒和9气囊。各浮体的参数見表1。同时管道与气囊和钢浮筒通过锚索连接，管道与浮吊船或履带吊通过吊缆相连。

采用气囊消气的工艺来对管道进行沉放[13-14]，如图3所示。该沉放过程主要分为3步。第一步：管道在钢浮筒和气囊的助浮下浮于水面，重心浮心在同一垂直线上，呈现稳定浮态。第二步：对管道注水加压，由于气囊和浮筒所提供浮力小于管道注水后的总重，管道将下沉，浮吊船和驳船开始受力。第三步：打开气囊气阀放气，同时吊缆也慢慢下放约1.53 m，整个管道受力将由气囊、钢浮筒、浮吊船、履带吊缓慢过渡到钢浮筒、浮吊船、履带吊上。最后，通过浮吊船和履带吊将管道摆正，协同下放吊缆，将管道沉入基槽中。

本文讨论的为气囊消气工艺中的第三步：时间上仅为气囊消气全过程，不包括气囊脱落后管道沉入基槽过程，如图3右两图所示。空间上，配合吊缆下放和气囊消气，管道从注满水的悬浮状态沿水下沉放约1.53 m。

该气囊消气过程是沉放作业最关键和危险的阶段，整个管道受力将由气囊、钢浮筒、浮吊船、履带吊缓慢过渡到钢浮筒、浮吊船、履带吊上。

由前述可知，该工程沉放过程涉及不规则的结构形状、多浮体耦合、流固耦合、浮力转移的均匀性、吊缆下放的协调性等问题。如控制不当，容易导致沉放过程出现受力不均、应力集中、吊缆张力过大等现象，引起工程事故。因此有必要对该沉放过程进行深入研究。

2 理论基础及数值计算模型

2.1 运动方程

沉放系统的运动方程为

Mp，a+Cp，v+Kp=Fp，v，t（1）

式中：Mp，a、Cp，v和Kp分别为系统的质量、阻尼和刚度矩阵;Fp，v，t为外部荷载;p，v和a分别为结构的位移、速度和加速度;t是时间。

在OrcaFlex中，选用悬链线法计算沉放系统的静平衡位置，采用全耦合时域分析方法对其进行动态时域分析。全耦合时域法通过反复耦合迭代求解复杂的模型的多体耦合问题，并能够更好地考虑几何构型的非线性效应、不规则的结构形状、浮体与浮体和锚泊系统与浮体的动态耦合效应等。即该方法能充分考虑吊缆、锚索、管道、气囊、钢浮筒之间的相互作用，从而更精确地计算管道和钢浮筒的动力响应以及吊缆和锚索张力。

2.2 风、流理论

风谱选用NPD谱，该谱的能量谱密度表达式为

SNPDf=320U10102z100.451+f0.4683.561（2）

式中：f为风频;U10为江平面以上10 m处的1 h内平均风速;z为距离江平面的高度。

作用在沉放系统中过江管道、钢浮筒、气囊等结构在x、y、z 3个方向的风力可按照下式计算[13]：

Fx=12Pρ（DnL）CdxVxVnFy=12Pρ（DnL）CdyVyVnFz=12Pρ（DnL）CdzVzVn（3）

式中：P为迎风面积比例系数;ρ为空气密度;Dn为法向阻力/升力直径;L为单位节段长度;Cdx，Vx，Cdy，Vy和Cdz，Vz分别为结构在（x，y，z）方向的拖曳系数和风相对结构在该方向的相对速度分量;Vn为风相对结构速度的法向分量。

关于沉放系统中管道、钢浮筒、气囊等结构物，常采用修正后的Morison公式来分别计算各结构的水动力荷载，该公式的表达式为[15-16]

Ff=（Δaf+CaΔar）+12ρwCdAVrVr（4）

式中：Ff是流体力;Δ是排水量;af是相对于大地的流体加速度;Ca是结构的惯性力系数;ar是相对于结构的流体加速度;ρw是水的密度;Vr是相对于结构的流速;Cd是拖拽力系数;A是阻力面积。

在沉放系统的沉放工程中，各结构的迎风迎流面积根据其在沉放系统中的空间位置确定。根据DNV-RP-C205 Environmental Conditions and Environmecotal Loads[17]和JTS 144-1-2010《港口工程荷载规范》[18]，结合工程经验，各结构物风力的拖曳力力系数取值为1.0，各结构物水流的拖曳力系数和惯性力系数均取值分别为1.2和1.0。

2.3 管道理论

如图4所示，基于集中质量法[19-21]，OrcaFlex软件将管道离散成若干连续线单元（即line 单元），管道质量、重力以及浮力作用于各个单元节点上，节点之间由无质量的弹簧连接，通过节点和弹簧的受力和变形来体现管道的运动响应。单元中心处的轴向弹簧和扭转弹簧及相应的阻尼器分别模拟管道的轴向和扭转特性，而节点两端处的转动弹簧和阻尼器用来模拟管道的弯曲特性。OrcaFlex依次通过5个阶段计算管道节点内力：① 轴力;② 弯矩;③ 剪力;④ 扭矩;⑤ 总荷载（重力、拖曳力、附加质量力等）。

2.4 Winch、Shape和6Dbuoy理论

模型采用Winch单元模拟实际工程中的吊缆[15-16]，该单元不承受压力，同时忽略重量、阻力和附加质量的影响。通过设置该单元的Specified Tension和Specified Payout Rate值来控制吊缆的预张力和下放速度，模拟实际工程中浮吊船和履带吊对管体的起吊工作，吊缆所受张力计算公式为

Fs=（l-l0）+c（dldt-dl0dt）×kl0（5）

式中：l和l0分别为吊缆在某一时刻的长度和初始长度;c和k分别为吊缆的阻尼系数和刚度。

Shape单元用于模拟吊臂，与Winch单元协同控制管体的起吊工作。模型采用6Dbuoy单元模拟钢浮筒，该单元有6个自由度（即3个平动和3个转动），主要承受重力、浮力和水动力载荷（包括线性水动力阻尼和力矩）。

2.5 数值计算模型

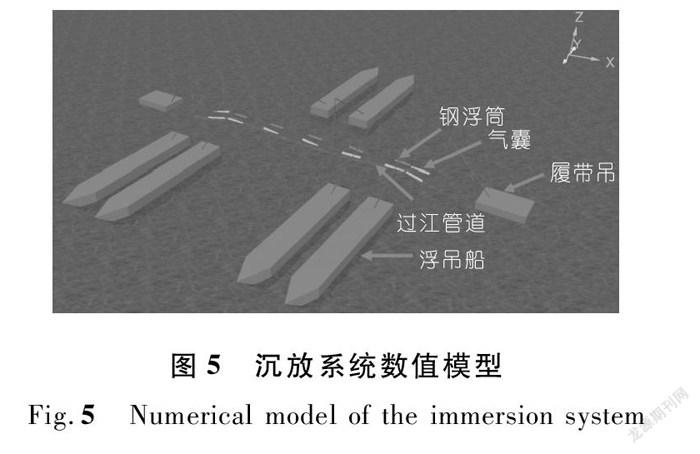
本文采用大型有限元软件OrcaFlex，对U型过江管道沉放系统的沉放施工进行模拟，即对气囊消气工艺中的第三步进行模拟（见图3）。因为第三步是一个瞬间变化较大的动态过程，控制难度大，施工风险大。在OrcaFlex软件中，管道和锚索均用Line单元来模拟;气囊和钢浮筒用6Dbuoy单元來模拟，即具有6个自由度的刚体;驳船和履带吊分别用Vessel单元和Shape单元来模拟;吊臂和吊缆分别用Shape单元和Winch单元来模拟。沿着管道长度方向每隔0.01 m划分一个网格，共有23 200个网格。最终建立的数值模型如图5所示。

为了便于计算，本文做了如下的简化和相应特殊处理。

（1） 实际的工程中，钢浮筒和气囊与管体均是由几组锚索连接，且钢浮筒和气囊与管体是紧密捆绑在一起的。在数值模拟中，简化成一根Line单元与管体刚性连接，通过把Line单元与管体的连接刚度设置成无穷大来模拟实际工程中捆绑在一起的情况。

（2） 由于实际工程中江面没有波浪且履带吊布置在江边两岸。因此在数值模拟中设置驳船和履带吊为固定结构，忽略其动力响应对沉放系统的影响。

（3） 在数值模拟中，通过在各气囊与管体的连接处添加一个线性递减的力来模拟气囊的消气过程。待气囊消完气后，利用单元生死功能，让气囊从管体脱落。

3 典型工况时域分析

本文典型工况下的气囊放气和吊缆下放时段分别为0～180 s和10～180 s，吊缆下放速度均为9 mm/s，管道内压为1.1 MPa，吊缆预张力均为5 kN，水流速度为0.35 m/s，参考平均风速为5 m/s。

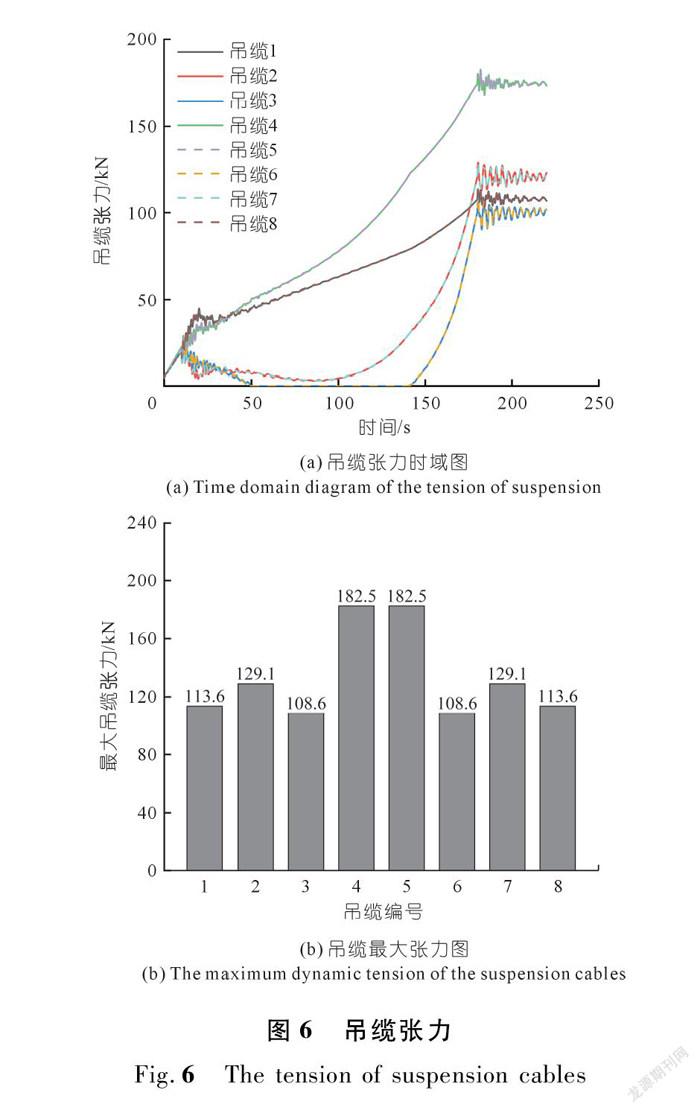
3.1 吊缆张力的时域分析

由图6（a）可知，在管道消气沉放过程中，各吊缆张力随着时间线性变化，待气囊消完气，即180 s之后，吊缆张力均逐渐趋向于平稳，最大幅值在气囊消气结束时刻附近。由图6（b）可知，各吊缆最大张力幅值分布呈现中间大、两头小的形态，其中中间位置处的吊缆（4号和5号）张力幅值约为182.5 kN，接近于驳船的最大承载能力196 kN，存在较大的施工风险。在实际工程中，建议对各吊缆张力进行实时监测，保证沉放施工的安全性。

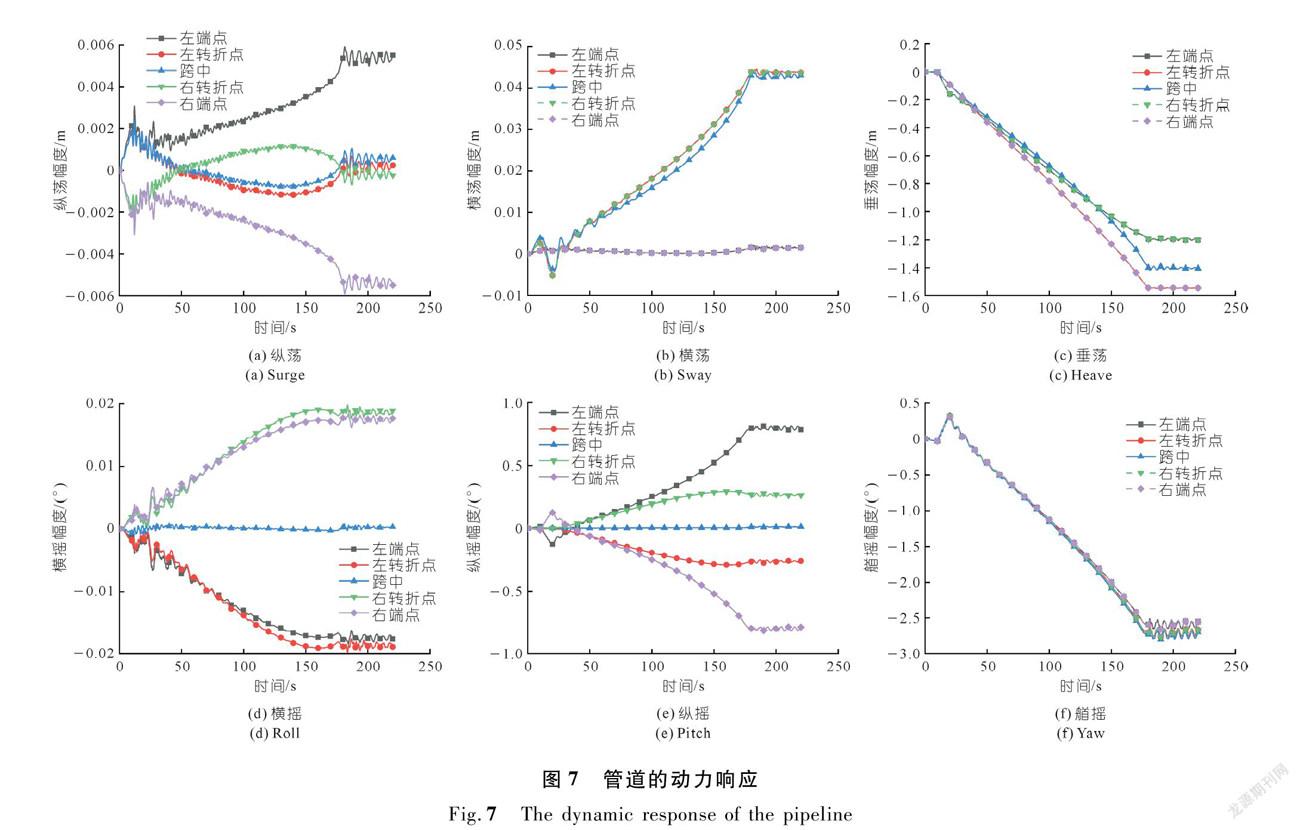
3.2 管道的动力响应

由图7可知：在沉放过程中，管道各处的动力响应除了垂荡方向外，其它方向的动力响应都很小，管道整体下降过程平稳可控。随着吊缆的下放，管道跨中和左右两端最大垂荡变化幅值分别约为1.40 m和1.55 m，这表明管体各处的下降高度并不一致，应该引起重视。在实际的工程中，为避免管道发生大幅倾斜，建议对管道各处的动力响应进行实时监测，把控管道各处的运动姿态，确保沉放过程的安全性。

3.3 管道的应力分布

由图8（a）可知，管道沿其长度方向的Von Mises应力最大值出现在中跨附近，大约在80 m 和130 m处，幅值约为66 MPa，远小于管道的屈服应力235 MPa。Von Mises应力曲线的线型与典型的欧拉梁理论比较符合，均呈现中间大，两头小的形态。图8（b）描述了管道沿其长度方向的拉伸应力，该应力沿管道长度方向的幅值变化不大，这是因为拉伸应力主要是由管道内压引起的。图8（c）描述了管道沿其长度方向的弯曲应力，其线型与Von Mises应力的线型高度相似，最大的弯曲应力约为55 MPa。同时，由图7（a～c）易知，管道以受弯为主。

3.4 锚索张力的时域分析

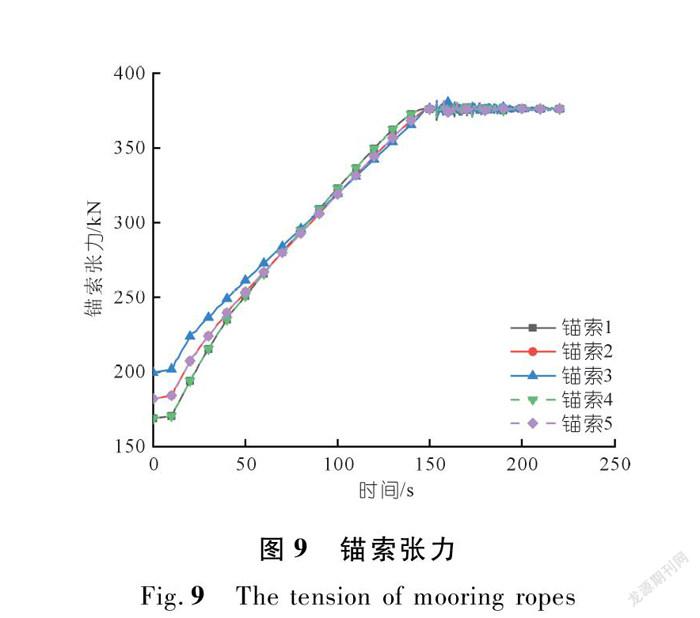
由图9可知，受沉放系统初始平衡状态的影响，初始时刻的锚索张力均分布在180 kN附近。在气囊消气过程中，锚索张力线性增加，约在170 s达到最大值，约为380 kN，之后保持平稳，意味着钢浮筒在170 s之后均已完全浸没。在实际的工程中，建议根据各钢浮筒的受力大小对其锚索长度和捆扎的松紧程度进行适当调节，让钢浮筒和管道的受力更均匀。

3.5 钢浮筒的动力响应

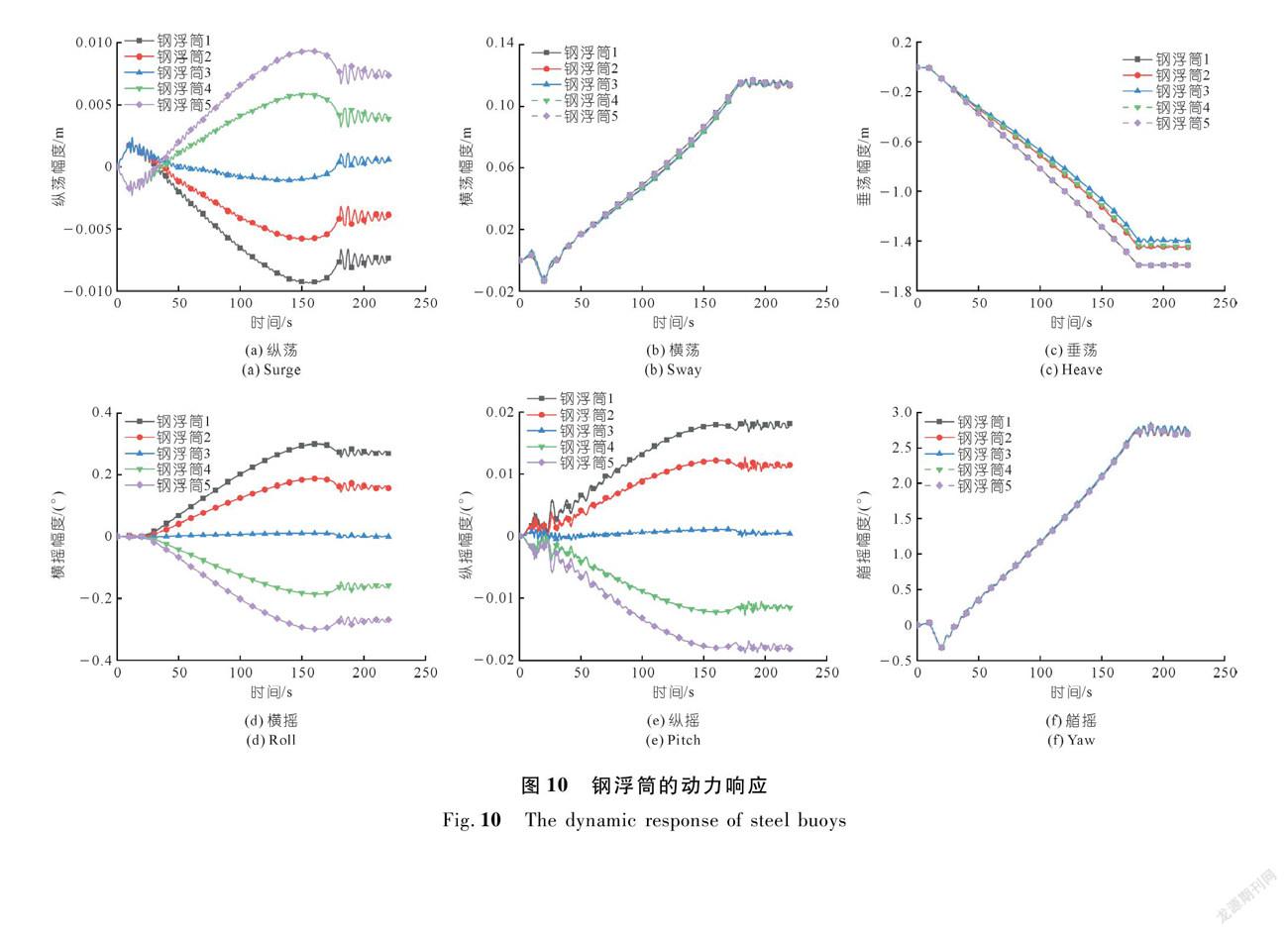
图10描述了钢浮筒的动力响应。由图可知：钢浮筒的动力响应与管道的动力响应变化规律高度相似，均呈现垂荡方向的动力响应较大，其余方向的动力响应很小，比较符合实际工程中钢浮筒与管道捆绑在一起的情况。在实际的工程中，建议合理把控各钢浮筒的浸没深度（钢浮筒的浸没深度与其提供给管道的浮力相关），提高管道整体受力的均匀性。

4 关键参数敏感性讨论

由前述典型工况的时域分析可知，管道和钢浮筒的动力响应、管道的应力、锚索张力均在安全可控的范围内，但是中间吊缆张力的最大值接近于驳船的最大起吊能力196 kN，存在较大的施工风险。为了降低施工风险，下面将着重探讨气囊消气方式、气囊消气时间、吊缆下放速度和吊缆下放的协调性对吊缆最大张力的影响，寻求最优施工方案。

4.1 气囊消气方式

消气方式有9个气囊同时消气、先左右两边的6个气囊消气后中间的3个气囊消气和先中间的3个气囊消气后左右两边的6个气囊消气。分别简称为同时、先两边后中间、先中间后两边。

由图11可知，先中间后两边的气囊消气方式对施工最不利，其4号和5号吊缆的最大张力幅值约为275 kN，远高于浮吊船的承载能力196 kN。先两边后中间的气囊消气方式对施工最优，相比于其它两种消气方式，其吊缆张力幅值和均匀性更好，幅值均不超过170 kN，在安全范围内。因此，实际工程中建议采取先两边后中间的气囊消气方式。

4.2 气囊消气时间

由图12可知，随着气囊消气时间的增加，各吊缆的最大张力均先减小后增加，表明气囊消气速度并非越慢越好。同时，当气囊消气时间为180 s和210 s时，各吊缆的最大张力均不超过200 kN，满足实际工程施工要求，建议优先选用。在实际工程中，应让气囊消气时间与吊缆下放速度相协调。

4.3 吊缆下放速度

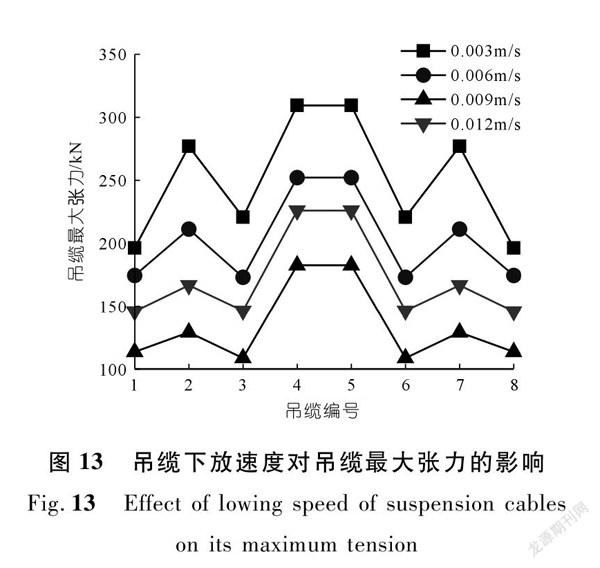
由图13可知，随着吊缆下放速度的增加，各吊缆的最大张力均先减小后增加。当吊缆下放速度为0.009 m/s时，各吊缆最大张力均满足施工要求，其余工况均有吊缆张力最大值超过浮吊船负荷。在实际工程中，吊缆下放速度应该与气囊消气速度相协调，避免吊缆张力过大。

4.4 吊缆下放的协调性

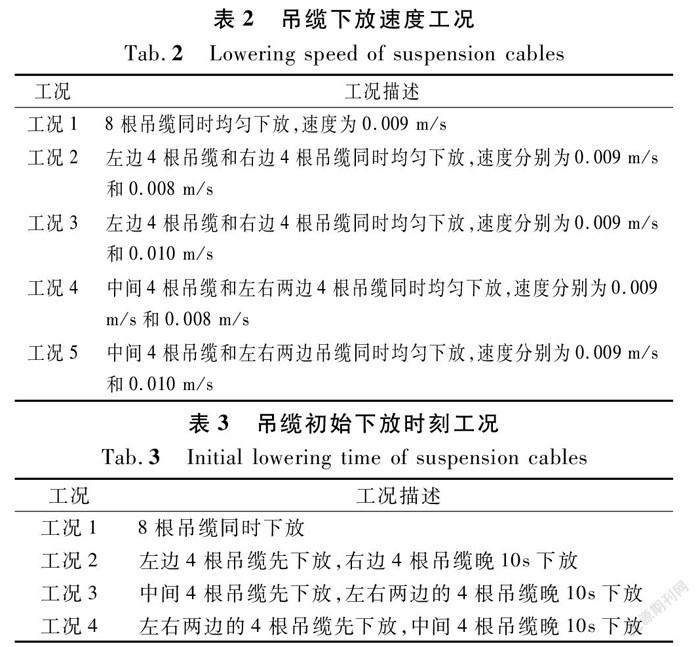
在实际工程中，由于客观因素的制约，难以保证沉放过程的协调性。为了贴合实际工程，特拟定了5种吊缆下放速度和4种吊缆初始下放时刻工况，分别见表2和表3，来探究吊缆下放的协调性对吊缆最大张力的影响。

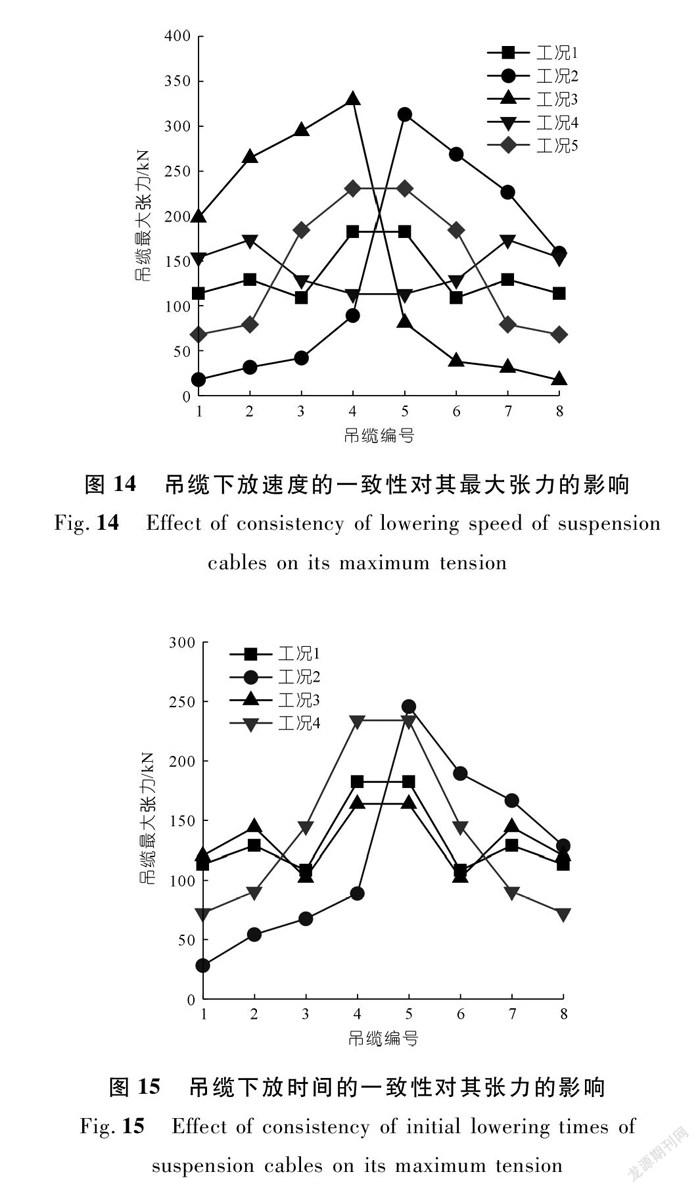
由图14可知：吊缆下放速度的一致性对吊缆最大张力的分布有显著的影响。与典型工况（即工况1）相比，无论采取剩余何种工况，均会使得吊缆下降速度比较慢的吊缆最大张力增加，吊缆下放速度比较快的吊缆最大张力减小。但是这不一定是不利的，如工况4，与典型工况相比，中间吊缆张力的最大张力反而变小了，整体的均匀性也较好。实际工程中，建议让中间的4根吊缆比左右两边的吊缆下放速度稍微慢一点（即工况4）。

由图15可知：吊缆初始下放时间的一致性对其最大张力分布影响也很大。与典型工况（即工况1）相比，无论采取剩余何种工况，均会使得初始下放时间慢的吊缆张力增加，初始下放时间快的吊缆张力减小。但是这不一定是不利的，如工况3，与典型工况相比，中间吊缆张力的最大值反而变小了，整体的均匀性也较好。实际工程中，建议让中间的4根吊缆比左右两边的吊缆初始下放时间稍微慢一点（即工况3）。

5 結论及施工建议

（1） 管道沉放过程中，所有吊缆张力的最大值约为182.5 kN，接近于浮吊船的最大承载能力196 kN，存在一定的安全隐患。管道和钢浮筒的动力响应安全平稳。管道沿其长度方向的Von Mises应力最大值出现在中跨附近，幅值约为65 MPa，远小于管道的屈服应力;锚索张力最大值约为380 kN。总体而言，过江管道沉放施工在安全可控的范围内。

（2） 实际工程中，有必要对各吊缆张力和管道各处的动力响应进行实时监测，实时把控吊缆受力和管道运动姿态，确保实际工程的安全性。

（3） 通过关键参数敏感性讨论，建议采用先两边后中间的气囊消气方式;气囊消气时间和吊缆下方速度应相互协调;中间吊缆的下放速度或初始下放时间稍慢于两边。

参考文献：

[1] 杜朝伟，王秀英.水下隧道沉管法设计与施工关键技术[J].中国工程科学，2009，11（7）：76-80.

[2] 左卫广，王永学.单驳船横荡运动对沉管管段横荡运动特性影响的试验研究[J].中国海洋平台，2015，30（2）：7-63，69.

[3] 应宗权，欧伟山，林美鸿.沉管隧道管节沉放过程中张力与运动响应的测试分析[J].现代隧道技术，2017，54（3）：162-168.

[4] CHEN Z J，WANG Y X，WANG G Y，et al.Frequency responses of immersing tunnel element under wave actions[J].Journal of Marine Science & Application，2009，8（1）：18-26.

[5] CHEN Z J，WANG Y X，WANG G Y.Time-domain responses of immersing tunnel element under wave actions[J].Journal of Hydrodynamics，2009，21（6）：739-749.

[6] 梁邦炎，卢普伟.沉管隧道长大管节海上施工物理模型试验思路与结果分析[J].水运工程，2013（6）：170-176.

[7] 吕卫清，吴卫国，苏林王，等.港珠澳大桥沉管隧道长大管节水动力性能试验研究[J].土木工程学报，2014，47（3）：138-144.

[8] HUANG G X，ZHANG N C，LAW A W K，et al.Motion response of immersing tunnel element under random waves[J].Ships and Offshore Structures，2016，11（6）：561-574.

[9] SONG Y，HUANG G X，PEI Y G，et al.Experimental study on the hoist tensions between the immersing tunnel element and floating pontoons under irregular waves[J].Coastal Engineering Journal，2015，57（4）：1-24.

[10] 杨璨，王永学，左卫广.双驳船锚碇沉管管段沉放过程的水动力特性试验研究[J].水动力学研究与进展，2018，33（1）：106-113.

[11] YANG C，WELLER S D，WANG Y X，et al.Hydrodynamic response of a submerged tunnel element suspended from a twin-barge under random waves[J].Ocean Engineering，2017，135：63-75.

[12] YANG C，WELLER S D，WANG Y X，et al.Experimental and numerical investigation on coupled motion characteristics of a tunnel element suspended from a twin-barge[J].Ocean Engineering，2018，153：201-214.

[13] 邓应康.大口径输水钢管过河沉管的设计与施工[J].中国给水排水，2011，27（6）：6-11.

[14] 韩峰，徐磊，金永苗.输水隧洞内压作用下衬砌结构破坏分析[J].人民长江，2020，51（增1）：149-152.

[15] OrcaFlex User Manual，Version 10.0 a.[Z].Orcina，2018.

[16] 边大勇，杜颖，刘建峰，等.海底埋设管线平管起吊运动分析[J].船舶工程，2015，37（12）：92-97.

[17] DNV-RP-C205.Environmental Conditions and Environmental Loads[S].Norway：Det Norske Veritas，2010.

[18] 交通运输部.港口工程荷载规范：JTS 144-1-2010[S].北京：人民交通出版社，2010.

[19] GONG S F，XU P，BAO S，et al.Numerical modelling on dynamic behaviour of deepwater S-lay pipeline[J].Ocean Engineering，2014，88：393-408.

[20] GONG S F，XU P.The influence of sea state on dynamic behaviour of offshore pipelines for deepwater S-lay[J].Ocean Engineering，2016，111：398-413.

[21] AMAECHI C V，WANG F C，HOU X N，et al.Strength of submarine hoses in Chinese-lantern configuration from hydrodynamic loads on CALM buoy[J].Ocean Engineering，2019，171：429-442.

（編辑：郑 毅）

Dynamic response analysis on U-shaped river-crossing pipeline during immersing construction process

XIAO Yangyang1，2，WU Zhiwen1，2，PAN Minghuang3，WU Changsong4，FANG Yiru1，2

（1.Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education，Guangxi University，Nanning 530004，China; 2.College of Civil Engineering and Architecture，Guangxi University，Nanning 530004，China; 3.Guangxi Asus Construction Engineering Co.，Ltd.，Nanning 53000，China; 4.Guangxi Dapu Expressway Co.，Ltd.，Nanning 530000，China）

Abstract：

The immersion process of a U-shaped pipeline involves problem of multi-body coupling，irregular structural shape，and coordination of suspension cables lowering，etc.To ensure construction safety and accuracy，based on the hydrodynamic analysis software OrcaFlex，a numerical analysis model for a U-shaped river-crossing pipeline in the immersion process was established.The dynamic tension of the suspension cables and mooring ropes，the dynamic response of the pipeline and its stress distributions along its length，and the dynamic response of the steel buoy were explored under typical case.The sensitivity of key parameters of the suspension cables tension was discussed.The results showed that the immersion process was safe and reliable in general，but improper operation could easily lead to excessive cable tension.In the actual construction，it was recommended to deflate the airbags at two ends of the pipeline firstly and deflate the airbags in the middle secondly，and the lowering speed of the suspension cables should be coordinated with the deflate time of the airbags，the lowering speed or initial lowering time of the middle suspension cables should be slightly later than that of the two sides suspension cables.It is necessary to real-time monitor the tension of the suspension cables and the dynamic response of the pipeline.This study can provide valuable references for the actual construction and other similar projects.

Key words：

U-shaped pipeline;construction of immersion pipeline;multi-body coupling;lowering suspension cables;immersion system;dynamic response;OrcaFlex