三峡水库汛期排沙效率研究

王玉璇 金中武 陈鹏

摘要：水库减淤调度是保障水库综合效益发挥的重要措施。以2003～2018年三峡库区主要水文站实测水沙数据为基础，统计分析了库区来水来沙规律，将库区按照沿程水文站布置分为3个库段，采用逐步回归的方法探讨了库区不同库段的输沙比与不同影响因素之间的相关情况，并建立了不同库段输沙比公式。结果表明：① 寸滩至清溪场库段输沙比的主要影响因素为流量沿程变化系数和水沙系数，清溪场至万县库段输沙比的主要影响因素为洪水滞留系数和含沙量，万县至庙河库段输沙比的主要影响因素为洪水滞留系数和流量;② 基于不同库段排沙比公式提出了提高排沙效率分段调度的新思路，即沙峰输移至清溪场站降低水位，输移至万县站继续加大下泄流量。研究成果可为三峡水库沙峰优化调度提供参考。

关 键 词：输沙比; 回归分析; 排沙调度; 三峡水库

中图法分类号： TV14

文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.05.003

0 引 言

三峡工程自2003年蓄水运用以来，经历了围堰蓄水期、初期运行期和试验性蓄水期3个阶段。随着库水位的逐渐抬升，库区河道水沙输移规律开始逐渐发生变化，水流流速沿程逐渐降低，水流挟沙能力明显减弱，导致泥沙沿程落淤。实测资料表明，2003年以来三峡库区泥沙淤积速度比预测情况明显减缓，但库区累计泥沙淤积量不断增加，逐渐侵占有效库容，年排沙比也从围堰蓄水初期的40%左右逐渐降低至试验性蓄水期的20%左右，有些枯水年份甚至仅达到7%。可见研究水库的排沙效率影响因素及变化趋势，进一步优化水库运行调度方案，进而提高水库的排沙效率，减缓三峡库区泥沙淤积进程，对充分发挥水库的综合效益有着重要意义。

排沙比问题一直都是学者们的研究重点。胡浩[1]、张欧阳[2]、张红武[3]分别对影响新疆克孜尔水库、洞庭湖、泾河东庄水库排沙比的因素进行了研究。张帅等[4]整理了小浪底水库汛期资料，验证分析了已有水库排沙比计算公式;王随继等[5]利用双累积曲线法对黄河下游河道实测水沙数据分成5个阶段进行了分析;张艳艳等[6]分析了黄河下游河道洪水资料并建立了排沙比回归模型;傅旭东等[7]从冲积河流输沙率关系入手，分别用不同的方法对黄河流域排沙比规律进行了研究。

关于三峡水库排沙比问题，陈桂亚等[8]深入研究了三峡水库各年年内水沙过程，指出库区河道特性、入库水沙条件以及坝前水位变化是影响排沙比的主要因素;董占地等[9]分析指出三峡水库坝前水位和出入库流量是影响排沙比的主要因素，此外入库沙量和泥沙粒径也对排沙比的大小有影响;黄仁勇等[10]探讨了三峡水库汛期排沙比与不同影响因素之间的关系，并引入洪水滞留系数建立了拟合程度较好的排沙比公式。

还有许多学者为提高水库排沙减淤调度提供了有力的技术支持。朱玲玲等[11]基于河段的泥沙冲淤规律和河床组成分析成果建立了一维数学模型，提出了悬移质泥沙走沙基本条件;张为等[12]针对梯级水库蓄水后三峡水库洪峰沙峰异步特性变化规律进行分析，并探讨了其主要原因;张地继等[13]采用实测资料分析和数值模拟的方法，对三峡库区沙峰的输移特性和衰减规律进行了系统研究;董炳江等[14-15]对三峡水库洪峰与沙峰传播特性进行了研究，并对2012，2013年和2020年沙峰排沙调度进行了分析总结调度。

然而对三峡库区的排沙比问题研究还不够充分，尤其是不同库段输沙比对来水来沙条件的响应以及变化趋势。本文以多个水文站实测逐日水沙数据为基础，分段对三峡水库典型场次洪水过程中输沙比与不同影响因素的相关关系进行分析，分别建立各库段汛期输沙比回归公式，并基于此提出了提高水库排沙效率的调度思路。

1 三峽水库来水来沙情况及资料选取

2003～2018年，三峡水库入库沙量23.36亿t，出库（黄陵庙站）沙量5.62亿t，不考虑区间来沙，水库淤积泥沙17.74亿t。从年际淤积变化情况来看，水库泥沙累计淤积强度呈现先增大、后减小的变化特点。特别是2012，2013年溪洛渡、向家坝水库蓄水运用后，上游来沙大幅度削减，水库淤积速度大幅下降，2014～2018年年均淤积泥沙约0.48亿t，仅为2003～2013年年均淤积量（1.39亿t）的34.7%。

实测地形资料表明：三峡水库在2003年6月至2006年10月的围堰蓄水期，库区累计淤积泥沙4.78亿m3，平均每年淤积泥沙1.59亿m3;在2006年10月至2008年10月的初期蓄水期，库区累计淤积泥沙3.20亿m3，平均每年淤积量为1.60亿m3;从2008年10月至2018年12月的试验性蓄水期，库区累计淤积泥沙8.64亿m3，平均每年淤积量0.84亿m3。

随着汛期坝前平均水位的抬升，水库的排沙比有所减小。在围堰发电期（汛期坝前平均水位为135m）、初期运行期（汛期坝前平均水位145 m）、2008年汛后进入试验性蓄水期后，水库年平均排沙比分别为31.9%，20.4%和18.3%。

本文收集三峡库区寸滩站、清溪场站、万县站、庙河站、黄陵庙站2003～2018年的水位、流量、含沙量、粒径级配等数据进行研究，各水文站水沙资料均为日均数据。选择长江干流寸滩站作为三峡水库入库控制站，坝下游黄陵庙站为三峡水库出库控制站。共选取了25场典型洪水过程，选取标准为洪峰流量大于30 000 m3/s，从入库寸滩站到出库黄陵庙站，逐站均有较为明显的沙峰过程，且沙峰必须要在各站依次出现，所选取的场次洪水过程均可完整地表现出洪峰与沙峰在库区的输移过程。

2 场次洪水排沙比影响因素研究

水库的排沙比与来水来沙条件、库区的河道边界条件以及水库的调度运用方式等密切相关。本文对三峡水库实测汛期典型场次洪水排沙比与不同影响因素的关系进行了统计分析，包括反映来水来沙情况的入库流量Q、入库含沙量S，以及反映水库调度运用情况的平均坝前水位Z。DEE15B9D-D559-4832-BDA5-284562D459EE

此外进一步考虑其他影响因素对场次洪水输沙排沙的影响，以及多因素的组合影响，进而全面反映库区排沙规律。影响因素包括：峰型系数Q/Qmax，即峰前平均流量与洪峰流量的比值;流量沿程变化系数Qout/Qin，即河段出口流量与进口流量之比，可以反映水流沿程衰减情况;水沙系数Q/S，反映水沙搭配情况;含沙量比粒径S/D50;坝前水位变化幅度ΔZ;滞洪库容V，既反映出库底河床形态，又可反映出坝前调度水位情况，可由水位库容曲线差值求得;洪水滞留系数V/Q，反映出入库洪水在库区滞留时间的长短，本文选择洪水滞留系数的形式为V×2/（Qin+Qout）。

整个库区从入库寸滩站到坝前庙河站总长度约620 km，鉴于库区各河段水沙条件、地形条件不尽相同，变动回水区接近于自然河道，而坝前库段水位较高流速较低，受水库调度情况影响较大，因此不同影响因素对排沙比的作用强度和方式都有所差异。为了进一步分析库区各库段输沙排沙的具体情况，将对整个库区分段进行研究，具体分为寸滩站-清溪场站、清溪场站-万县站、万县站-黄陵庙站3个库段。

分别对各库段输沙比与各单一影响因素进行回归分析，得到线性回归决定系数统计见表1。可见在沿程各个库段，排沙情况均与峰型系数和坝前水位变化幅度的相关性较差;相对于滞洪库容而言，输沙比与洪水滞留系数和平均坝前水位的相关性较好，且在清溪场站-万县站和万县站-黄陵庙站影响最为显著，在寸滩站-清溪场站库段影响较差;寸滩站-清溪场站库段输沙比与含沙量的相关性较差，庙河站-黄陵庙站库段输沙比与流量的相关性较好。

在寸滩站-清溪场站库段，输沙比与流量沿程变化系数和水沙系数的相关性较好;在清溪场站-万县站库段，除洪水滞留系数和平均坝前水位外，输沙比还与清溪场站含沙量的相关性较好;在万县站-黄陵庙站库段，除洪水滞留系数和平均坝前水位外，输沙比还与万县站流量及含沙量的相关性较好。

3 场次洪水排沙比公式研究

3.1 寸滩站-清溪场站库段输沙比

由上文对单一影响因素的研究得出：在寸滩站-清溪场站库段Qout/Qin和Q/S对输沙排沙有较强影响，线性回归决定系数均大于0.3。为进一步考虑各因素之间的非线性作用，以及两不同因素之间相互叠加作用对库区输沙排沙的影响，将影响因素的高阶项以及交叉项引入到多项式回归表达式中。分别用y表示输沙比η寸-清，x1表示Q清/Q寸，x2表示Q/S。以上述两个变量为自变量，以输沙比为因变量，构建多项式回归公式如下：

Y=a1x1+a2x2+a3x1x2+a4x12+a5x22+ε（1）

式中：ai（i=0，1，2，…，5）为模型参数;ε为随机误差。

采用逐步回归的方法，从所建立的多元回归模型中筛选出对因变量影响显著的自变量，剔除共线变量和不显著变量，进而用数学表达的方式描述出所筛选出的自变量与因变量之间的关系。逐步回归结果表明：Q清/Q寸和Q/S组合项是寸滩站-清溪场站库段输沙排沙的主要影响因素，模型回归决定系数R2为0.803。为了进一步探究输沙比与Q清/Q寸和Q/S两个自变量之间更优的量化关系，构建多元非线性回归方程如下：

η寸-清=Q清Q寸αQ寸S寸β（2）

式中：为系数，α和β为指数，η寸-清为寸滩站-清溪场站库段输沙比，Q清/Q寸为流量沿程变化系数，Q寸/S寸为水沙系数。代入数据，具体结果为

η寸-清=47.998Q清Q寸0.934Q寸S寸0.067=47.998Q0.934清Q0.867寸S0.067寸

R2=0.870

（3）

计算结果与实测值比较结果见图1。

3.2 清溪场站-万县站库段输沙比

由上文对单一影响因素的研究可知：在清溪场站-万县站库段Sin，Qin，V/Q共3個因素都对输沙排沙有较强影响，线性回归决定系数均大于0.3。为进一步考虑各因素之间的非线性作用，以及两不同因素之间相互叠加作用对库区输沙排沙的影响，将影响因素的高阶项以及交叉项引入到多项式回归表达式中。分别用y表示输沙比η清-万，x1表示S清，x2表示Q清，x3表示V清-万×2/（Q清+Q万）。以上述3个变量为自变量，以输沙比为因变量，构建多项式回归公式如下：

Y=a1x1+a2x2+a3x3+a4x1x2+a5x1x3+

a6x2x3+a7x12+a8x22+a9x32+ε（4）

采用逐步回归的方法，从所建立的多元回归模型中筛选出对因变量影响显著的自变量，剔除共线变量和不显著变量，进而用数学表达的方式描述出所筛选出的自变量与因变量之间的关系。

式（4）逐步回归结果表明S清和V清-万×2/（Q清+Q万）组合项是清溪场站-万县站库段输沙排沙的主要影响因素，模型回归决定系数R2为0.724。为了进一步探究输沙比与S清和V清-万×2/（Q清+Q万）两个自变量之间更优的量化关系，构建多元非线性回归方程如下：

η清-万=V清-万Q清+Q万2α×S清β（5）

式中：为系数，α和β为指数，η清-万为清溪场站-万县站库段输沙比，V清-万×2/（Q清+Q万）为库段洪水滞留系数（V清-万为清溪场-万县库段的库容），S清为清溪场站含沙量。代入数据，具体结果为

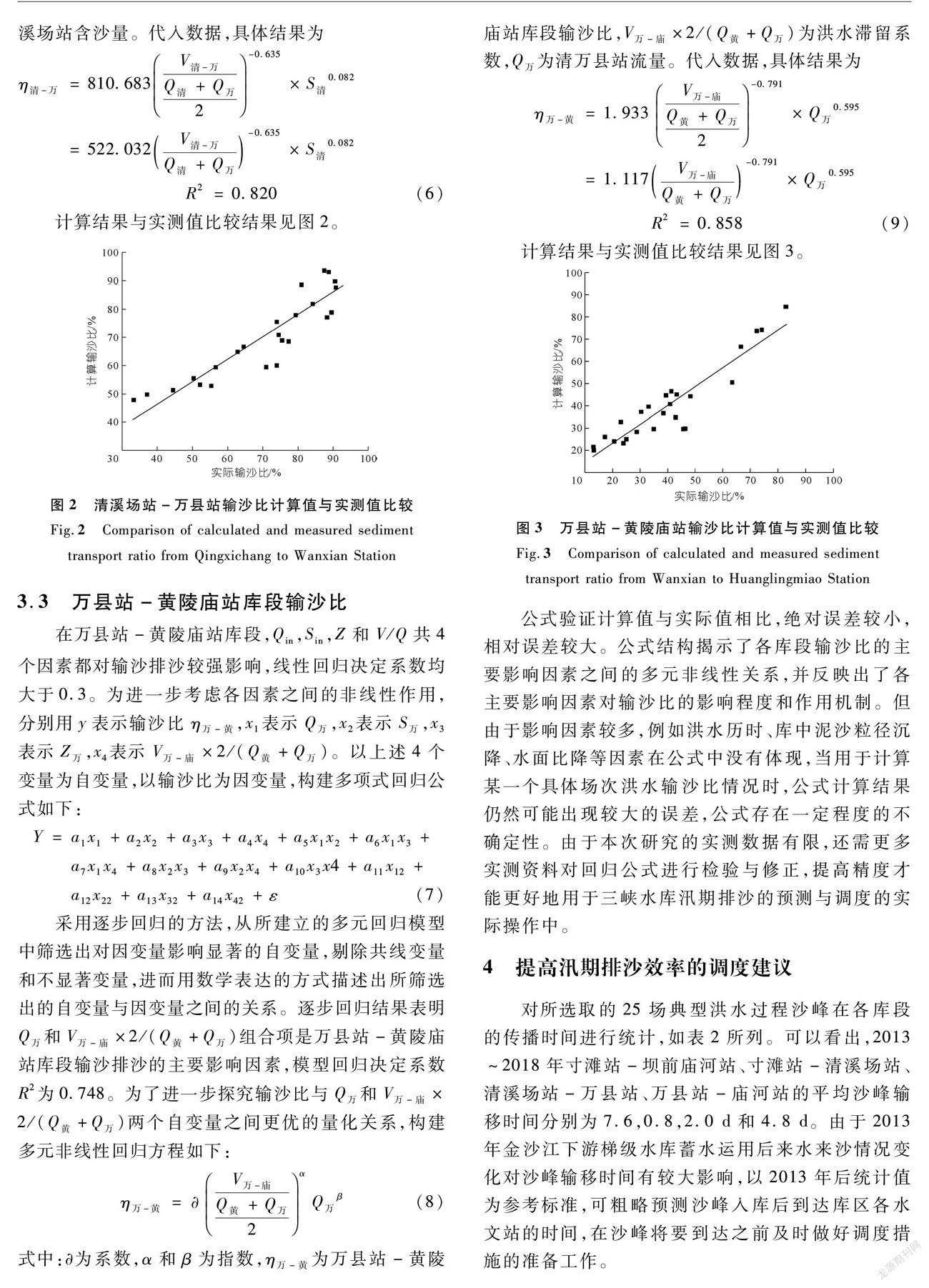
η清-万=810.683V清-万Q清+Q万2-0.635×S清0.082

=522.032V清-万Q清+Q万-0.635×S清0.082

R2=0.820

（6）

计算结果与实测值比较结果见图2。

3.3 万县站-黄陵庙站库段输沙比

在万县站-黄陵庙站库段，Qin，Sin，Z和V/Q共4个因素都对输沙排沙较强影响，线性回归决定系数均大于0.3。为进一步考虑各因素之间的非线性作用，分别用y表示输沙比η万-黄，x1表示Q万，x2表示S万，x3表示Z万，x4表示V万-庙×2/（Q黄+Q万）。以上述4个变量为自变量，以输沙比为因变量，构建多项式回归公式如下：DEE15B9D-D559-4832-BDA5-284562D459EE

Y=a1x1+a2x2+a3x3+a4x4+a5x1x2+a6x1x3+

a7x1x4+a8x2x3+a9x2x4+a10x3x4+a11x12+

a12x22+a13x32+a14x42+ε（7）

采用逐步回归的方法，从所建立的多元回归模型中筛选出对因变量影响显著的自变量，剔除共线变量和不显著变量，进而用数学表达的方式描述出所筛选出的自变量与因变量之间的关系。

逐步回归结果表明Q万和V万-庙×2/（Q黄+Q万）组合项是万县站-黄陵庙站库段输沙排沙的主要影响因素，模型回归决定系数R2为0.748。为了进一步探究输沙比与Q万和V万-庙×2/（Q黄+Q万）两个自变量之间更优的量化关系，构建多元非线性回归方程如下：

η万-黄=V万-庙Q黄+Q万2αQ万β（8）

式中：为系数，α和β为指数，η万-黄为万县站-黄陵庙站库段输沙比，V万-庙×2/（Q黄+Q万）为洪水滞留系数，Q万为清万县站流量。代入数据，具体结果为

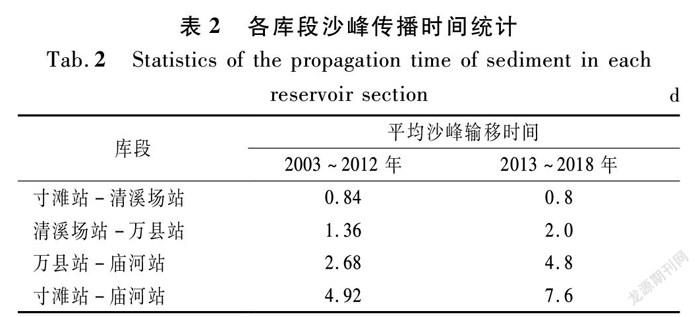
η万-黄=1.933V万-庙Q黄+Q万2-0.791×Q万0.595

=1.117V万-庙Q黄+Q万-0.791×Q万0.595

R2=0.858

（9）

计算结果与实测值比较结果见图3。

公式验证计算值与实际值相比，绝对误差较小，相对误差较大。公式结构揭示了各库段输沙比的主要影响因素之间的多元非线性关系，并反映出了各主要影响因素对输沙比的影响程度和作用機制。但由于影响因素较多，例如洪水历时、库中泥沙粒径沉降、水面比降等因素在公式中没有体现，当用于计算某一个具体场次洪水输沙比情况时，公式计算结果仍然可能出现较大的误差，公式存在一定程度的不确定性。由于本次研究的实测数据有限，还需更多实测资料对回归公式进行检验与修正，提高精度才能更好地用于三峡水库汛期排沙的预测与调度的实际操作中。

4 提高汛期排沙效率的调度建议

对所选取的25场典型洪水过程沙峰在各库段的传播时间进行统计，如表2所列。可以看出，2013～2018年寸滩站-坝前庙河站、寸滩站-清溪场站、清溪场站-万县站、万县站-庙河站的平均沙峰输移时间分别为7.6，0.8，2.0 d和4.8 d。由于2013年金沙江下游梯级水库蓄水运用后来水来沙情况变化对沙峰输移时间有较大影响，以2013年后统计值为参考标准，可粗略预测沙峰入库后到达库区各水文站的时间，在沙峰将要到达之前及时做好调度措施的准备工作。

库区沙峰输移受来水来沙直接影响，因此可以将沙峰入库时水量沙量的大小作为沙峰调度开始的依据。选取175 m试验性蓄水期出库沙峰含沙量大于0.2 kg/m3的10组场次洪水资料进行分析，其中9场入库沙峰含沙量均大于2.0 kg/m3;此外当寸滩站出现沙峰时，有9场寸滩站的流量均大于30 000 m3/s;当出库黄陵庙站的沙峰含沙量大于0.2 kg/m3时，在沙峰到达出库黄陵庙站时刻黄陵庙站的出库流量均大于30 000 m3/s，

如果出库黄陵庙站沙峰含沙量太小，则沙峰调度将没有实际意义，将入库寸滩站沙峰含沙量大于2.0 kg/m3和入库寸滩站出现沙峰时该站流量大于30 000 m3/s作为沙峰调度开始实施的两个依据，可基本保证出库沙峰含沙量能大于0.2 kg/m3，且当沙峰输移至坝前时，三峡水库沙峰调度增泄排沙流量应大于30 000 m3/s。

根据库区沿程各段输沙比主要影响因素构建的回归公式可以得出：在寸滩站-清溪场站库段，流量沿程变化系数和来水来沙情况对输沙排沙的影响较为显著;在清溪场站-坝前庙河站库段，洪水滞留系数是该段输沙的主要影响因素;万县站-坝前庙河站库段输沙比还受到流量的较大影响。因此可以在沙峰到达清溪场站时继续降低坝前水位促进排沙，减缓沙峰衰减，在沙峰到达万县站时在降低坝前水位的前提下，进一步加大流量增泄排沙直至沙峰出库。此外在沙峰调度的过程中应该尽量保持库水位在较低条件下运行，且出库增泄流量越大越好。当下泄流量需要从电站以外其他泄水建筑物排除时，应优先选择排沙孔泄洪排沙，有利于坝底高浓度泥沙的排出，提高场次洪水排沙比。

5 结 论

本文以三峡水库2003～2018年库区各水文站实测水沙数据为基础，分析了典型场次洪水的排沙比在沿程不同库段与不同影响因素之间的关系，得到了拟合程度较好的各库段输沙比回归公式，并对沙峰调度方案提出建议。研究主要得到以下结论。

（1） 各影响因素在三峡库区不同库段对输沙比的影响程度有所不同，水沙系数、流量沿程变化系数等反映来水来沙情况的系数对寸滩站-清溪场站库段影响较为显著;滞洪库容、洪水滞留系数等反映水位调度的系数对清溪场站-黄陵庙站库段影响较为显著。

（2） 在寸滩站-清溪场站库段，输沙比受来水来沙情况的影响较大，主要影响因素为流量沿程变化系数和水沙系数;在清溪场站-万县站库段，输沙比的主要影响因素为洪水滞留系数和含沙量;万县站-黄陵庙站库段输沙比的主要影响因素为洪水滞留系数和流量。

（3） 使用不同库段输沙比的主要影响因素分别建立了回归公式，回归系数R2均大于0.8，拟合效果较好。但由于影响因素较多，例如反映洪水历时、库中泥沙粒径沉降、水面比降等因素在公式中没有体现。

（4） 为保证沙峰调度的排沙效率达到出库沙峰含沙量大于0.2 kg/m3，将入库寸滩站沙峰含沙量大于2.0 kg/m3和入库寸滩站出现沙峰时该站流量大于30 000 m3/s作为沙峰调度开始实施的两个依据。

（5） 以研究得出的库区各库段输沙比的主要影响因素差异为基础，提出了提高排沙效益的沙峰调度优化方案，即在沙峰到达清溪场站时继续降低坝前水位促进排沙，在沙峰到达万县站时在降低坝前水位的前提下，进一步加大流量增泄排沙直至沙峰出库。DEE15B9D-D559-4832-BDA5-284562D459EE

參考文献：

[1] 胡浩.新疆克孜尔水库运行库水位对汛期排沙比的影响分析[J].广西水利水电，2019（1）：45-47.

[2] 张欧阳，熊明.洞庭湖排沙比变化及影响因素分析[J].人民长江，2006，36（12）：117-119.

[3] 张红武，张欧阳，张俊华，等.泾河东庄水库排沙试验研究[J].水力发电学报，2004（4）：82-87.

[4] 张帅，夏军强，李涛.小浪底水库汛期排沙比研究[J].人民黄河，2018，40（1）：7-11.

[5] 王随继，刘慰，颜明，等.黄河下游汛期输沙效率和排沙比阶段性变化及其主控因素分析[J].水土保持研究，2020，27（2）：104-111.

[6] 张艳艳，吴保生，傅旭东.黄河下游河道场次洪水输沙特性分析[J].水力发电学报，2012，31（3）：70-76.

[7] 傅旭东，姜立伟，吴保生，等.黄河下游河道场次洪水排沙比及其不确定性[J].中国科学（技术科学），2010，40（4）：349-357.

[8] 陈桂亚，袁晶，许全喜.三峡工程蓄水运用以来水库排沙效果[J].水科学进展，2012，23（3）：355-362.

[9] 董占地，胡海华，吉祖稳，等.三峡水库排沙比对来水来沙的响应[J].泥沙研究，2017，42（6）：16-21.

[10] 黄仁勇，谈广鸣，范北林.三峡水库蓄水运用后汛期洪水排沙比初步研究[J].水力发电学报，2013，32（5）：129-133，152.

[11] 朱玲玲，葛华，董炳江，等.三峡水库175 m蓄水后库尾河段减淤调度控制指标研究[J].地理学报，2021，76（1）：114-126.

[12] 张为，李昕，任金秋，等.梯级水库蓄水对三峡水库洪峰沙峰异步特性的影响[J].水科学进展，2020，31（4）：481-490.

[13] 张地继，董炳江，杨霞，等.三峡水库库区沙峰输移特性研究[J].人民长江，2018，49（2）：23-28，68.

[14] 董炳江，陈显维，许全喜.三峡水库沙峰调度试验研究与思考[J].人民长江，2014，45（19）：1-5.

[15] 董炳江，许全喜，杨成刚，等.2020年三峡水库沙峰排沙调度分析[J].水利水电快报，2021，42（1）：27-32.

（编辑：胡旭东）

Study on sediment transport efficiency of Three Gorges Reservoir during flood season

WANG Yuxuan，JIN Zhongwu，CHEN Peng

（River Department，Changjiang River Scientific Research Institute，Wuhan 430010，China）

Abstract：

Reservoir sediment ejection regulation is an important measure to ensure the comprehensive benefits of reservoirs.Based on the measured data of water and sediment in the main hydrological stations of the Three Gorges Reservoir （TGR） from 2003 to 2018，this paper analyzed the law of water and sediment in the reservoir area.According to the layout of hydrological stations along the river，the reservoir area was divided into three sections，and the correlation between sediment transport ratio and different influencing factors in different sections was discussed by stepwise regression，and the formulas of sediment transport ratio in different reservoir sections were established.The results showed that：（1） the main influencing factors for sediment transport ratio from Cuntan to Qingxichang section were discharge variation coefficient and water-sediment coefficient，the main influencing factors for Qingxichang to Wanxian section were flood detention coefficient and sediment concentration，and the main influencing factors for Wanxian to Miaohe section were flood detention coefficient and discharge.（2） Based on the formula of sediment transport ratio of different reservoir sections，a new idea to improve the efficiency of sediment discharge was put forward，namely lowering the water level when the sand peak transporting to Qingxichang station，and continuing to increase the discharge when the sand peak transporting to Wanxian station.The research results can provide reference for the optimal operation of the Three Gorges Reservoir.

Key words：

sediment transport ratio;regression analysis;sediment ejection regulation;Three Gorges ReservoirDEE15B9D-D559-4832-BDA5-284562D459EE