缺陷对氮化硅导热性能影响的模拟研究

陈大业,陈 鹏,钱家盛,夏 茹,伍 斌

(安徽大学化学化工学院，合肥 230601)

0 引 言

氮化硅作为一种性能优良的陶瓷材料，因具有良好的力学性能、抗热冲击性和耐磨损性能，而被广泛应用于化工、机械、能源、半导体等领域。除却优异的机械性能外，研究表明β型氮化硅也具有较高的导热性能。Haggerty等[1]通过计算提出在室温下β型氮化硅的理论热导率可达 200～320 W·m-1·K-1。Hirosaki等[2]利用分子动力学方法，探究发现β型单晶氮化硅在300 K下，其沿a轴与c轴的热导率分别可达170 W·m-1·K-1和450 W·m-1·K-1。氮化硅不仅具有优异的力学性能，还具有良好的理论热导率，是一种具有良好发展前景的高功率电子器件的基板材料,因此制备出具有高导热性的氮化硅显得尤为重要。

为了获得具有高导热性能的氮化硅陶瓷，Wang等[3-6]开发了金属氢化物、硅化物等不同于传统氧化物的新型烧结助剂，调节了液相组分，实现对氮化硅陶瓷晶界相以及晶格氧含量的调控，获得了具有较高热导率的氮化硅陶瓷。然而由于工艺条件的限制，体系仍不可避免产生空位、杂质等缺陷，这些缺陷的存在导致实际制备得到的氮化硅材料热导率仍远低于理论热导率[7]，另外在现有的实验技术下，对氮化硅材料微观状态下缺陷的分布等研究还存在一些困难。

分子动力学模拟以其独特的优势，常被用于研究缺陷对材料导热性能的影响。Islam等[8]利用分子动力学方法探究了多种缺陷类型(如点空位、双空位与混合空位)对二维碳化硅材料导热性能影响，发现点空位对二维碳化硅导热性能影响最大。Khalkhali等[9]通过分子动力学方法研究了碳杂质对硅纳米线导热性能影响，结果表明当引入少量碳杂质时，硅纳米线热导率急剧降低。目前，氮化硅材料缺陷方面的模拟研究相对较少，而缺陷又严重影响着材料的导热性能，因此，利用分子动力学模拟方法探究缺陷对氮化硅热导率的影响显得尤为重要。

分子动力学计算材料热导率通常采用两种方法：一种是基于波动耗散理论利用Green-Kubo公式对材料的热传导性能进行计算的平衡态分子动力学(EMD)方法；另一种是通过对体系施加扰动，利用傅里叶定律对材料的热传导性能计算的非平衡态分子动力学(NEMD)方法[10]。NEMD方法相较于EMD方法具有计算时间更短、精确度更高等优点。

本文利用NEMD方法，探究氮化硅热导率随着缺陷比例和温度的变化规律，研究缺陷分布以及氮原子不同晶格位置上的缺陷对氮化硅热导率影响，研究结果为实验上制备高导热氮化硅陶瓷提供理论指导和新的思路。

1 模型与方法

1.1 模型构建

本文选取β型氮化硅作为研究对象，首先建立了氮化硅的全原子模型，如图1(a)所示。模型中硅原子和氮原子以3 ∶4的比例形成三维晶格结构。为了研究空位和氧杂质对氮化硅体系导热性能的影响规律，通过在全原子模型的晶格中删去若干氮原子得到具有空位的氮化硅模型。为了模拟实验制备过程中混入晶格的杂质氧，将部分氧原子掺入到氮化硅晶体中，并以替代氮原子的位置存在，如图1(b)所示。研究中采用了尺寸为2.65 nm×3.05 nm×23.37 nm与6.61 nm×7.64 nm×23.37 nm的两种模型体系，为方便设置体系的缺陷分布状态和选择晶格位置，采用第二种模型体系用于探究缺陷分布与不同晶格位置缺陷对氮化硅热导率影响。

1.2 模拟方法

本研究中，氮化硅体系中原子之间的相互作用采用Tersoff势能[11-13]描述，体系的热力学平衡和导热的计算过程均在大规模原子/分子并行计算模拟器(LAMMPS)[14]中完成。在模拟过程中，z轴方向被设置为自由边界条件，其余方向采用周期性边界条件，时间步长设置为0.1 fs。体系首先采用共轭梯度法进行能量最小化，其次分别在等温等压(NPT)系综和正则(NVT)系综中运行1 ns，以获得稳定的结构；之后换成微正则(NVE)系综继续松弛0.5 ns，使体系能量和温度达到充分稳定的状态。

为了研究氮化硅体系的导热性能，采用NEMD方法计算体系的热导率。导热方法示意图如图1(c)所示，体系两端设置为固定端，固定端两侧分别设置为冷区和热区，经过热平衡后对体系施加扰动，待形成稳定的温度梯度后，采用傅里叶定律计算体系热导率。热导率的计算方法如式(1)和(2)所示。

(1)

(2)

式中：k为热导率；J为热流密度；dT/dz为z轴方向的温度梯度；ΔE为冷热区能量变化；Δt为冷热区能量变化对应的时长；A为体系垂直z轴方向的横截面积。

图1 模型与方法示意图：(a)原始氮化硅模型；(b)引入缺陷的氮化硅模型；(c)导热方法示意图Fig.1 Schematic diagram of model and method: (a) original silicon nitride model; (b) silicon nitride model with defects introduced; (c) schematic diagram of heat conduction method

2 结果与讨论

2.1 缺陷比例对氮化硅体系导热性能影响

反应烧结和热压烧结是实验制备氮化硅的两种主要工艺方法，目前的制作工艺过程中都不可避免出现一些缺陷，例如：(1)晶格中部分氮原子缺失，即氮原子的位置出现空位；(2)晶格中部分氮原子被杂质氧原子替代。为了探究两种典型缺陷对氮化硅导热性能的影响规律，设计了氮空位(nitrogen vacancy)和氧掺杂(oxygen doping)两种缺陷体系，以模拟前述两种缺陷状态。定义缺陷比例 (defect ratio)为缺陷的数量(缺失的氮原子数量或氧原子的数量)与体系中全部原子数目的比例。氮化硅模型体系中的缺陷比例从小到大依次设定为0.52%、0.98%、1.5%、1.97%、2.5%。

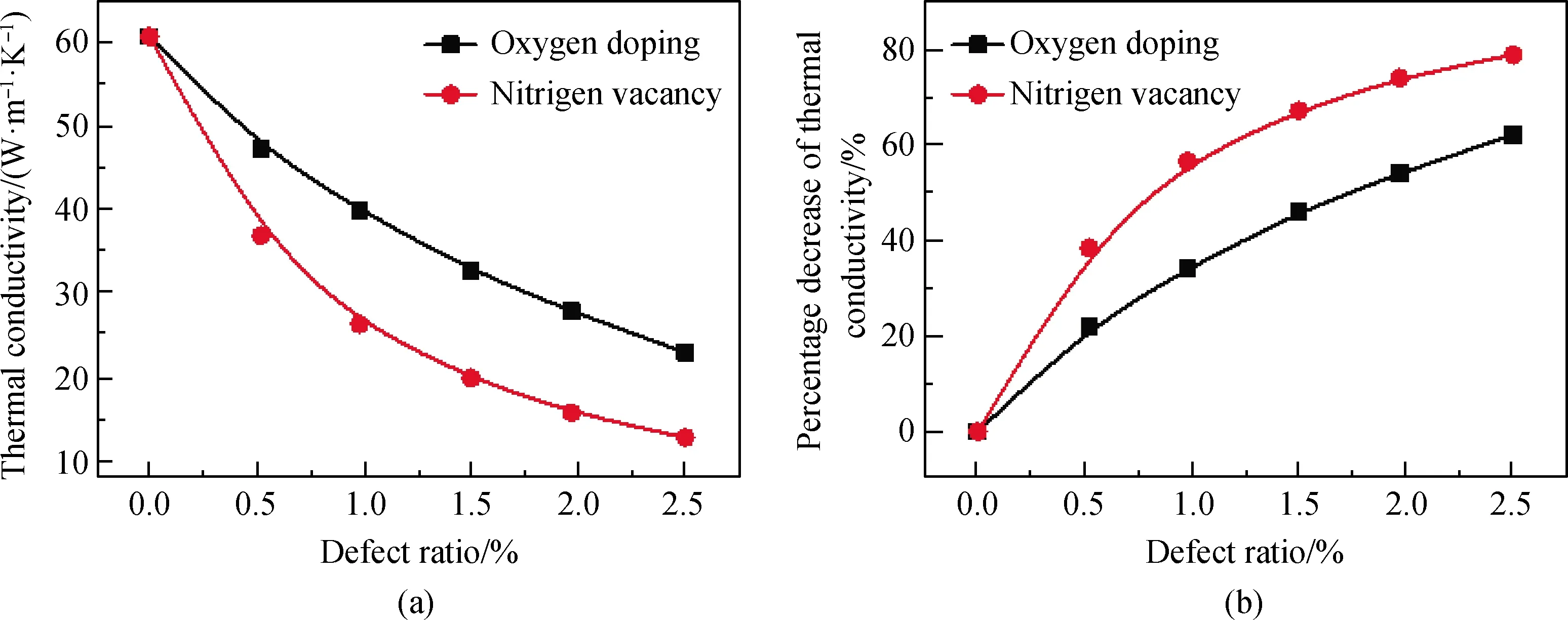
图2 缺陷比例对氮化硅导热性能影响：(a)不同缺陷比例下氮化硅体系热导率; (b)不同缺陷比例下氮化硅体系热导率降低百分比Fig.2 Effect of defect ratio on thermal conductivity of silicon nitride： (a) thermal conductivity of silicon nitride system with different defect ratios； (b) percentage reduction of silicon nitride thermal conductivity under different defect ratios

模拟缺陷比例对氮化硅导热性能的影响如图2所示。由图2(a)可知，随着缺陷比例的增加，氮化硅热导率迅速降低[15]。由图2(b)可知，当缺陷比例为2.5%时，氮空位缺陷体系相较于无缺陷体系，热导率下降了78%，氧掺杂缺陷体系热导率下降了62%。研究结果表明同等比例下的缺陷，氮空位缺陷体系热导率更低。因此，在制备高导热的氮化硅陶瓷基体时，提高氮化硅的纯度和消除空位对于提高材料的导热性能具有极其重要的影响。

2.2 缺陷比例对氮化硅体系导热性能影响的声子态密度分析

分子动力学中研究的热传导是以声子振动形式体现的，体系的声子振动情况可以通过声子态密度[16-19]来描述，声子态密度(PDOS)是通过对速度自相关函数进行傅里叶变换得到。为了分析缺陷比例对氮化硅体系导热性能的影响规律，计算了初始状态下的完整晶体(pristine)与不同缺陷比例下氧掺杂体系以及氮空位体系下的声子态密度，计算方法如式(3)所示。

(3)

式中：Vj(t)代表粒子j在时间t的速度；N为系统原子数；w代表频率；i代表虚数单位。

计算结果如图3(a)、(b)所示，随着缺陷比例的增加，氧掺杂以及氮空位(nitrogen vacancy)这两种缺陷体系的声子态密度曲线，相较于完整晶体皆出现了峰值软化的现象，且伴随着缺陷比例的增加，峰值不断软化，尤其在25～30 THz处最为明显，图中已经通过箭头加以区分。这表明声子在传输过程中受到杂质氧原子和空位的影响，声子散射情况愈加严重，这和氮化硅热导率下降趋势一致。之后比较了缺陷比例为0.52%与0.98%下氧掺杂以及氮空位这两种缺陷体系的声子态密度，如图3(c)和(d)所示，结果表明，相同缺陷比例下，具有氮空位的氮化硅体系相较于引入杂质氧原子的体系，前者具有更低的峰值，这表明氮空位对体系声子传输过程中产生的负面影响要大于杂质氧原子所带来的，这也解释了为什么氮空位缺陷体系相较于氧掺杂缺陷体系，前者具有更低的热导率。

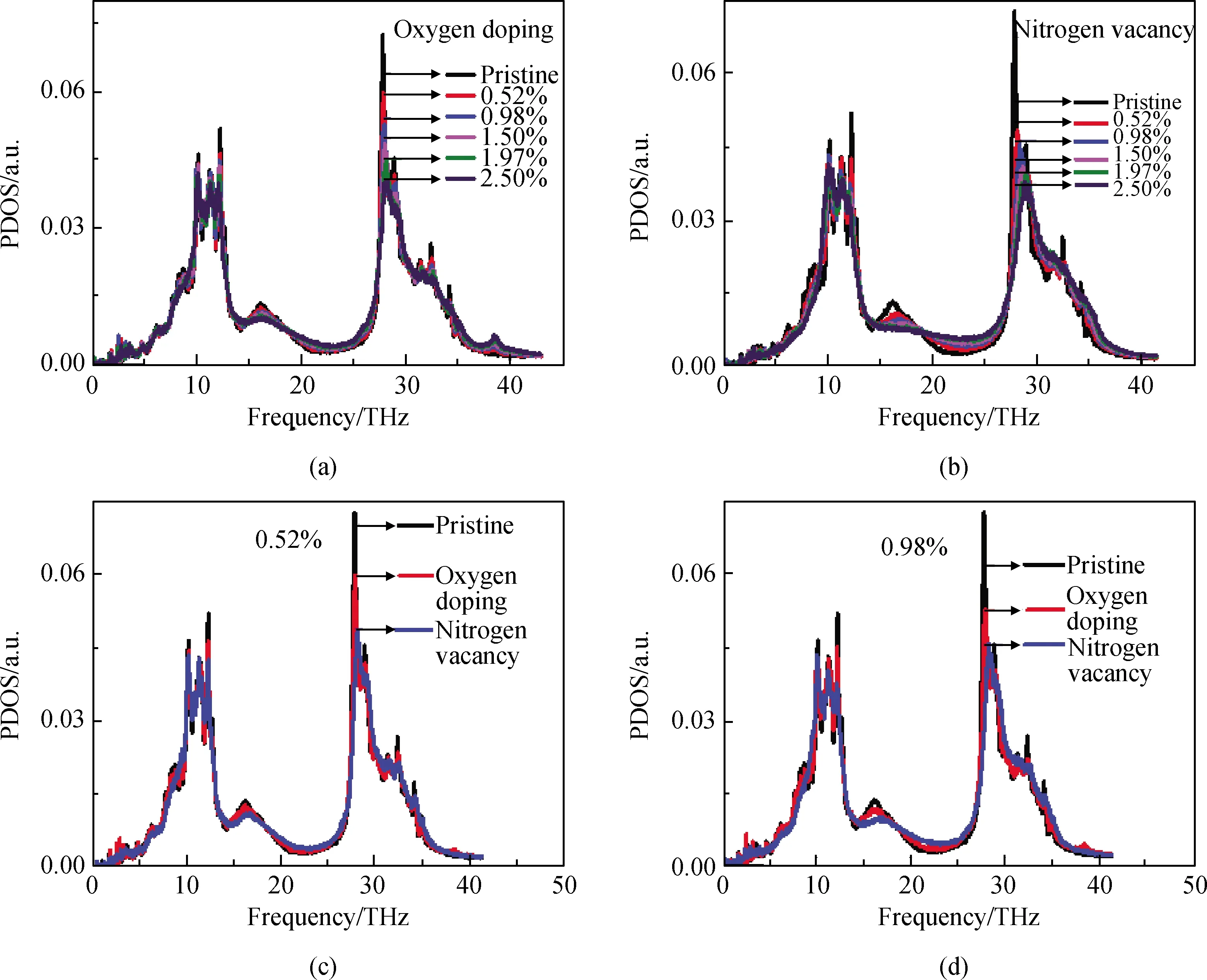
图3 不同缺陷比例下氮化硅体系声子态密度图：(a)氧掺杂缺陷体系;(b)氮空位缺陷体系； 完整体系与缺陷比例为0.52%(c)以及0.98%(d)体系下的声子态密度曲线对比Fig.3 Phonon density diagram of silicon nitride system with different defect ratios: (a) impurity oxygen defect system; (b) nitrogen vacancy defect system; comparison of phonon density of states curves for the pristine system and defect ratios of 0.52% (c) and 0.98% (d)

2.3 温度对氮化硅体系导热性能影响

为了探究温度对氮化硅导热性能的影响规律，分别计算了温度为300 K、400 K、600 K、800 K、1 000 K下的完整氮化硅晶体和不同缺陷比例下氧掺杂以及氮空位这两种缺陷体系的热导率。研究结果如图4(a)和(b)所示，随着体系温度的升高，氮化硅缺陷与无缺陷的体系，热导率都呈明显的下降趋势[20]。从图4(c)可以看出，控制相同缺陷比例时，随着温度升高，完整晶体热导率最高，氮空位缺陷体系热导率最低。从图4(d)可以看出，当温度从300 K上升到1 000 K时，无缺陷体系的热导率下降了64%，缺陷比例为0.52%的氧掺杂与氮空位这两种缺陷体系，热导率分别下降约60%和53%。这说明温度对完整晶体的导热性能影响更大，并且从图4(a)、(b)中，发现随着缺陷比例的增加，氮化硅的导热性能随温度变化越不敏感。这是因为随着空位/氧杂质比例的增加，原本完整的晶体结构已经受到了严重的破坏，声子传输能力已经远远不如完整晶体，此时温度升高对体系声子传输带来的负面影响已经不够剧烈，而完整晶体因为晶体结构未受到破坏，声子传输能力仍然很强，此时温度升高对体系声子传输造成的影响比较剧烈。

图4 温度对氮化硅体系导热性能影响：(a)氧掺杂缺陷体系;(b)氮空位缺陷体系； (c)完整与缺陷体系热导率随温度变化对比;(d)完整与缺陷体系热导率随温度变化下降百分比Fig.4 Influence of temperature on thermal conductivity of silicon nitride system: (a) impurity oxygen defect system; (b) nitrogen vacancy defect system; (c) thermal conductivity of pristine and defect systems comparison with temperature; (d) percentage decrease in thermal conductivity of pristine and defect systems with temperature

2.4 温度对氮化硅体系导热性能影响的声子态密度分析

为了进一步分析温度对氮化硅体系导热性能的影响规律，分别计算了完整晶体、氧掺杂缺陷体系以及氮空位缺陷体系的声子态密度，缺陷体系的比例控制在0.52%。如图5(a)～(c)所示，随着温度的升高，在25～30 THz处，不同状态下的氮化硅声子态密度曲线的峰值同样出现软化的现象(图中已经通过箭头加以区分),这是随着温度的升高，Umklapp散射增加所致[21]。温度升高，Umklapp散射增加，声子平均自由程减少，所以体系热导率急剧降低。相同温度下，完整晶体热导率仍高于氧掺杂以及氮空位这两种缺陷体系，并且氮空位缺陷体系热导率最低。这与图5(d)所示结果一致，在400 K下，完整晶体声子态密度曲线峰值最高，氮空位体系的声子态密度曲线峰值最低，这表明此时有缺陷体系声子传输过程中受到的负面影响是高于完整体系的，并且氮空位缺陷体系所受影响最大。

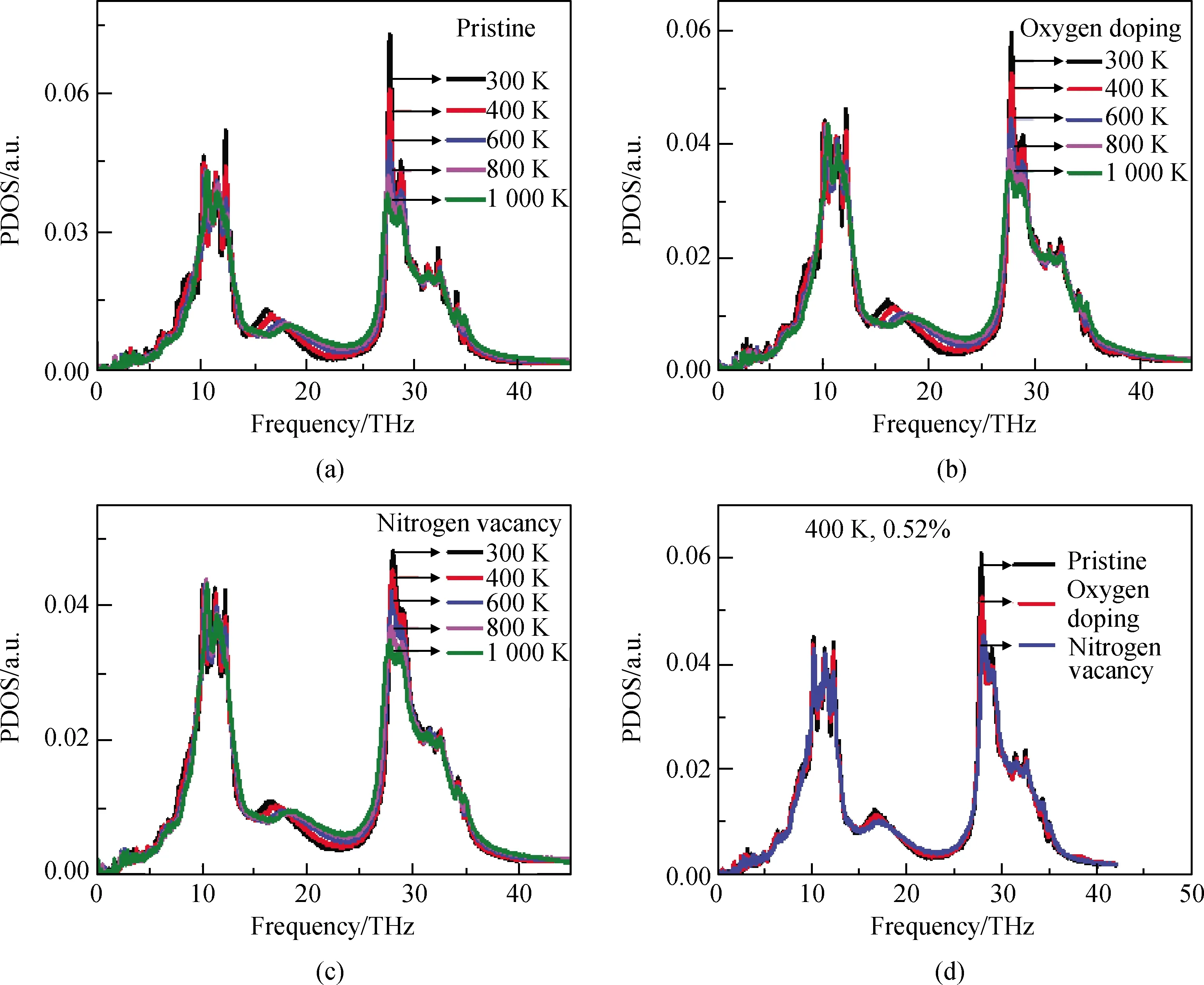
图5 不同温度下氮化硅体系的声子态密度图：(a)完整晶体；(b)氧掺杂缺陷体系；(c)氮空位缺陷体系； (d)400 K 下完整与缺陷体系声子态密度曲线对比Fig.5 Phonon density diagram of silicon nitride system at different temperatures: (a) pristine system; (b) impurity oxygen defect system; (c) nitrogen vacancy defect system; (d) pristine at 400 K comparison with the phonon density of states curves of the defect system

2.5 缺陷的分布对氮化硅体系导热性能影响

为了探究杂质氧原子或空位分布状态对氮化硅导热性能的影响规律，本文设计了缺陷在氮化硅基体内不同分布状态下的模型，如图6(a)所示。Disperse代表体系缺陷原子均匀分散，V-L-aggregation代表体系缺陷原子低程度聚集，V-H-aggregation代表体系缺陷原子较高程度聚集，V-aggregation代表体系缺陷原子高程度聚集。之后计算缺陷原子的径向分布函数，用来表征缺陷原子的聚集程度，如图6(b)所示，随着缺陷逐渐沿着导热通路中间聚集，径向分布函数的峰值逐渐增高。此外还计算了不同缺陷分布状态下氮化硅的热导率，如图6(c)所示，发现缺陷由原本随机分布逐渐向导热通路中间聚集时，氮化硅热导率急剧降低。这是因为当缺陷集中于导热通路中间时，处于中间层的导热通路被严重破坏，热流在跨越中间层的过程中受到严重阻碍，导致体系热导率急剧降低。研究结果为实验上制备高导热氮化硅提供新的思路，即实验上制备导热性能优良的氮化硅材料，需要尽量避免杂质原子或空位集中在传热方向上。

2.6 晶格位置缺陷对氮化硅体系导热性能影响

通过反应或热压烧结制备氮化硅材料过程中，体系不可避免会产生缺陷，其中杂质氧原子往往会以替代氮原子的形式存在于氮化硅中。图7(a)为氮化硅的单胞模型，图中较大的原子代表硅原子，其余为氮原子，在氮化硅晶体中氮原子存在N1和N2两种晶格位置，标识的氮原子所处位置即N1位置，剩下的原子为N2位置，然而对于氧原子替代哪种晶格位置上的氮原子会对氮化硅导热性能影响更大，这点实验上却难以观察。因此，通过使用分子动力学的方法，来探究氮原子处于不同晶格位置上的缺陷对体系导热性能影响。研究结果如图7(b)所示，相同比例下的缺陷，氮原子处于N2位置相较于N1位置，无论是被氧原子替代还是产生相应的空位，其热导率都要更低，这也可以给实验上制备高导热氮化硅提供一个思路，若是可以控制氮原子缺陷位置，即便是产生相同比例的缺陷，氮化硅导热性能同样得到有效改善。

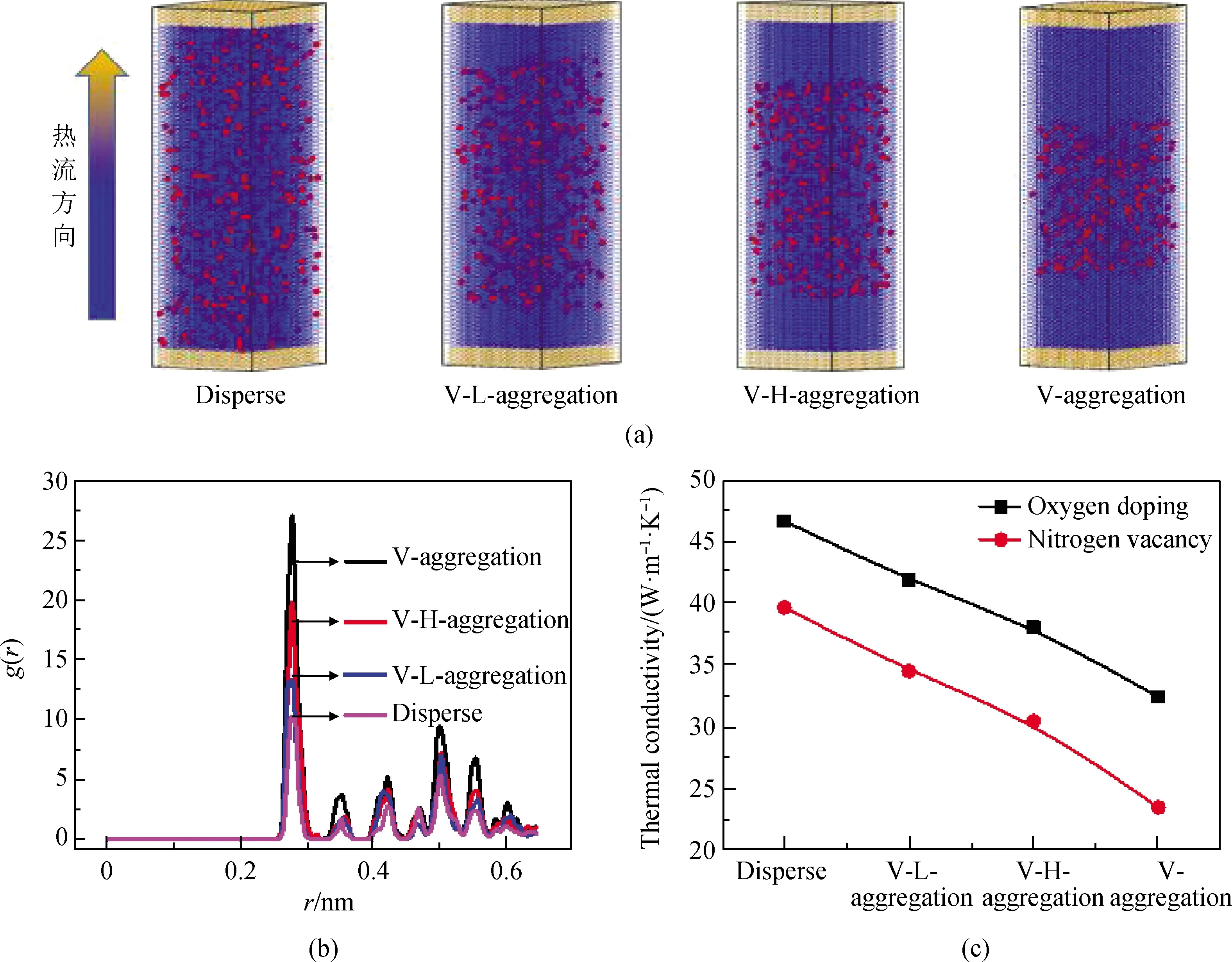
图6 缺陷的分布状态对氮化硅导热性能影响：(a)模型示意图；(b)径向分布函数图； (c)不同缺陷分布状态下氮化硅热导率Fig.6 Influence of defect distribution on thermal conductivity of silicon nitride: (a) Schematic diagram of the model; (b) radial distribution function diagram; (c) thermal conductivity of silicon nitride under different defect distribution states

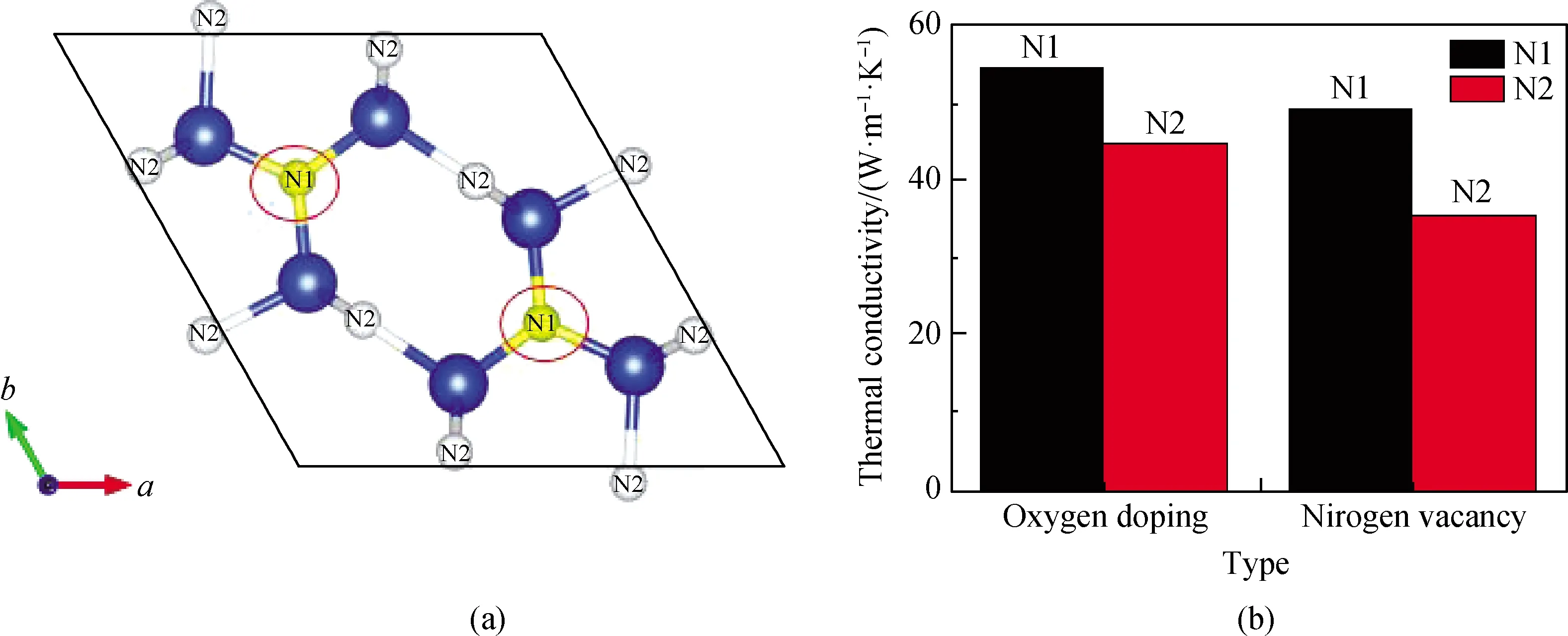
图7 氮原子不同晶格位置缺陷对体系导热性能影响：(a)结构示意图；(b)缺陷在不同晶格位置下体系的热导率Fig.7 Influence of defects on different lattice positions of nitrogen atoms on the thermal conductivity of the system: (a) schematic diagram of the structure; (b) thermal conductivity of the system with defects at different lattice positions

3 结 论

本文利用分子动力学方法研究缺陷对氮化硅导热性能影响，模拟结果表明：

(1)随着氮化硅基体内杂质氧原子与氮空位的增加以及温度的升高，体系的热导率急剧降低。通过计算得到的声子态密度表明，随着缺陷比例的增加以及温度升高，声子在传输过程中受到严重的阻碍。

(2)相同缺陷比例条件下，缺陷集中在导热通路中间相较于缺陷随机分布的氮化硅体系，前者具有更低的热导率。

(3)氮化硅晶体中氮原子存在N1和N2两种晶格位置，N2位置上产生的缺陷对体系导热性能影响更大。