无耦合PCNN 频域特性分析

邓翔宇，吕亚辉，陈 岩

（西北师范大学物理与电子工程学院，兰州 730070）

0 概述

随着生物电子技术的发展，人工神经网络的研究也不断取得进展。文献［1］根据哺乳动物视觉皮层神经元信号传导特性，构建一种新的神经网络模型。文献［2］将神经网络模型改进为用于图像处理领域的模型，并命名为脉冲耦合神经网络（Pulse Coupled Neural Network，PCNN）。传统的PCNN 模型可分为耦合连接和无耦合连接两种模式，被广泛应用于图像分割［3-4］、图像融合［5-6］、图像去噪［7-8］、图像检索［9-10］以及图像边缘检测［11-12］等领域。通常将无耦合连接模式下的网络称为无耦合PCNN。无耦合PCNN 模型虽然没有耦合连接项，但是保留了PCNN模型的核心子系统部分，具有网络参数少的特点，近年来，逐渐被应用于图像处理领域［13］。

研究人员通过对图像进行信息提取或变换域处理，融合PCNN 模型进行参数自适应设定，并应用于特定的图像处理领域。文献［14］通过SIST（Shift Invariant Shearlet Transform）方法获取图像的高频子带和低频子带频率，使用SOM（Self-Origanizing Maps）网络进行初步分类，之后融合改进的PCNN 模型，获得较优的图像分割效果。文献［15］利用非下采样轮廓波变换对图像进行多尺度和多方向分解，获得低通子带和多个带通方向子带，并将其与改进后的PCNN 模型相结合用于多聚焦图像融合。文献［16］基于图像NSCT（Non-Subsampled Contourlet Transform）域变换提取图像的边缘特征，提出一种结合自适应PCNN 的红外与可见光图像融合算法。文献［17］通过建立待分割图像统计特性与PCNN 神经元动态特性之间的直接关系，完成简化PCNN 的参数自适应设置。文献［18］通过计算分割图像的最小交叉熵，提出一种新的基于循环迭代的自适应图像分割算法，用于改进PCNN 阈值分割机制。此外，研究人员通过对网络模型进行理论分析，以解释网络本质特性并进行参数的自适应设定。文献［19］分析改进后PCNN 网络的动态行为，明确PCNN 的动态行为特性受网络参数变化的影响，并提出网络参数确定准则，使得所有神经元只点火一次。文献［20］通过分析PCNN 中神经元的脉冲发放周期，定义了动态比，以得出近似的脉冲发放周期公式。文献［21］根据PCNN 工作机理的时域分析，提出一种在点火神经元没有完全灭火时不允许灭火神经元重新点火的网络工作模式，并用于图像的自适应分割。然而，上述PCNN 模型的研究都只是从时域方面或图像本身所含信息方面分析参数与模型之间的关系，在网络本质的特性挖掘方面还存在着一定的局限性和片面性。

本文从频域角度对无耦合PCNN 的网络参数与模型特性之间的关系进行分析。通过推导动态门限子系统的频率响应函数，揭示动态门限子系统具有低通特性，同时分析参数对动态门限子系统频率响应的影响，推导无耦合连接时PCNN 有效点火时刻方程、动态门限衰减频率和脉冲发放频率的方程，解释无耦合PCNN 的网络参数对网络频域特性的影响。

1 基本概念

1.1 数学模型

无耦合PCNN 模型由输入子系统、动态门限子系统和输出子系统组成，分别如式（1）～式（3）所示［22］：

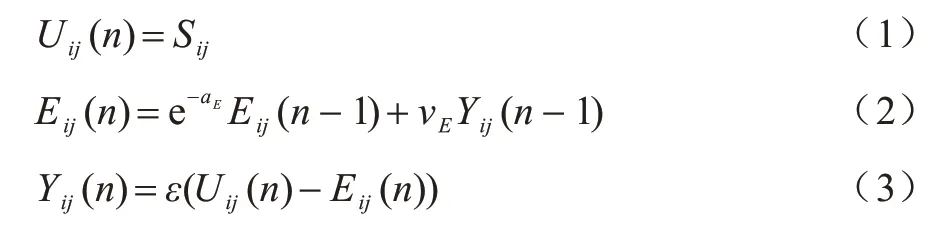
其中：i、j为本神经元像素坐标点；n为迭代次数；Sij为系统的输入，常为归一化之后的像素灰度值；aE、vE为控制动态门限子系统的2 个网络参数。模型的输出子系统由单位阶跃函数构成，决定该神经元的脉冲发放状态。当神经元的输入值大于动态门限值时，神经元发放脉冲又称为神经元点火；否则，神经元灭火。

1.2 第1 次有效点火时刻

在前期研究中［23］已经得知无耦合PCNN 的第1 次神经元点火时刻不受网络参数的影响，因此重点分析了网络的第2 次点火时刻，又称为第1 次有效点火时刻（所有输入值在第1 次迭代时发生的点火称为无效点火，其后各次点火为有效点火），通过推导所得第1 次有效点火时刻N1如式（4）所示：

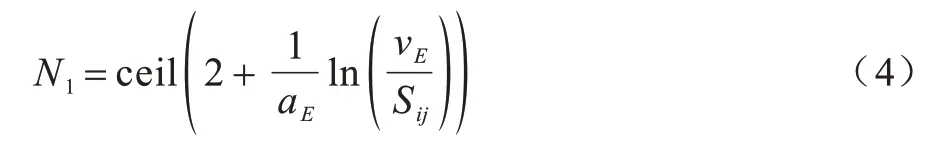
由于网络数学模型为差分方程，因此当理论点火时刻为小数时，实际点火时刻为下一个整数时刻。在第1 次有效点火时刻计算中引入向上取整函数ceil。由式（4）可知，当灰度值Sij=0时，无法发生第1次有效点火。本文主要针对网络输入的有效点火时刻及输入灰度值Sij为1/255～1 时，网络所表现出的特性。

2 无耦合PCNN 频域分析

在实际图像的处理过程中，输入子系统的输入为图像对应像素点的灰度值，是简单的线性系统。本文对式（1）表示的输入子系统不展开分析。由于无耦合网络的时域特性完全受参数影响，因此本文对于网络的频域分析，根据动态门限子系统的频域特性分析参数对动态门限子系统的影响，将式（1）、式（2）和式（3）联系起来，分别分析网络中动态变量Yij(n)和Eij(n)的频域特性与参数之间的关系。

2.1 动态门限子系统的频域特性

2.1.1 系统函数

动态门限子系统是无耦合PCNN 模型的核心子系统，由差分方程式（2）表示，对式（2）进行z变换可得式（5）：

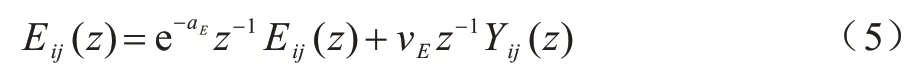
动态门限子系统的系统函数如式（6）所示：

根据系统函数HE(z)可知，动态门限子系统没有零点，只有1 个极点z=。此时系统函数的收敛域为。当aE>0 时，子系统的收敛域包含单位圆，此时的系统是一个因果稳定系统。当aE≤0 时，系统不稳定。因此，无耦合PCNN 参数aE的取值范围为(0，+∞)。

2.1.2 频率响应与参数影响分析

动态门限子系统的系统函数HE(z)收敛域包含单位圆，根据z变换与傅里叶变换之间的关系可得子系统的频率响应，如式（7）所示：

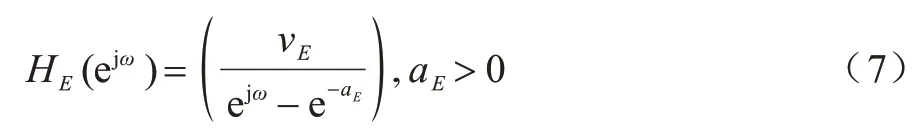
根据频率响应函数HE(ejw)可得其幅频响应，如式（8）所示：

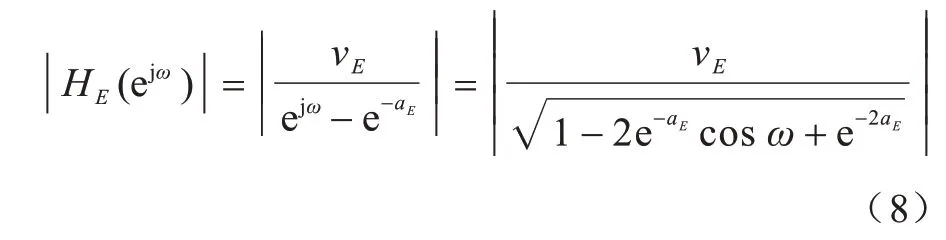
由式（8）可知，参数aE和vE共同控制子系统的幅值特性。改变参数aE和vE，在ω∈(0，π)范围内观察到的子系统HE(ejω)的幅频特性曲线变化如图1 所示。

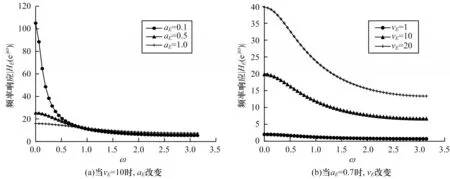
图1 参数对动态门限子系统幅频特性的影响Fig.1 Influence of parameters on amplitude-frequency characteristics of the dynamic threshold subsystem

从图1（a）可以看出，参数aE主要影响幅频响应峰值与谷值之间的差值，aE越小，差值越大，此时系统低频分量的幅值较大，高频分量的幅值较小，使得子系统具有较优的低通特性。从图1（b）可以看出，参数vE主要影响幅频特性的幅值大小，vE越大，幅频响应的幅值也将增大。因此，无耦合PCNN 模型的动态门限子系统具有低通特性，不同的网络参数使得动态门限系统表现出不同的低通特性。子系统的低通特性主要受参数aE影响，参数vE主要影响子系统的幅值大小。

2.2 网络脉冲发放频域特性

2.2.1 有效点火脉冲方程

无耦合PCNN 是一个非线性系统，其神经元的输入与神经元的脉冲发放频率之间存在非线性关系。当参数aE=0.5，vE=5 时，在不同灰度值下神经元的动态门限和点火时刻的变化曲线如图2 所示。从图2 可以看出，单个神经元的脉冲点火过程和动态门限衰减过程都具有周期性，在输入值Uij的激励下，输出Yij(n)和Eij(n)以一定的周期发放脉冲。

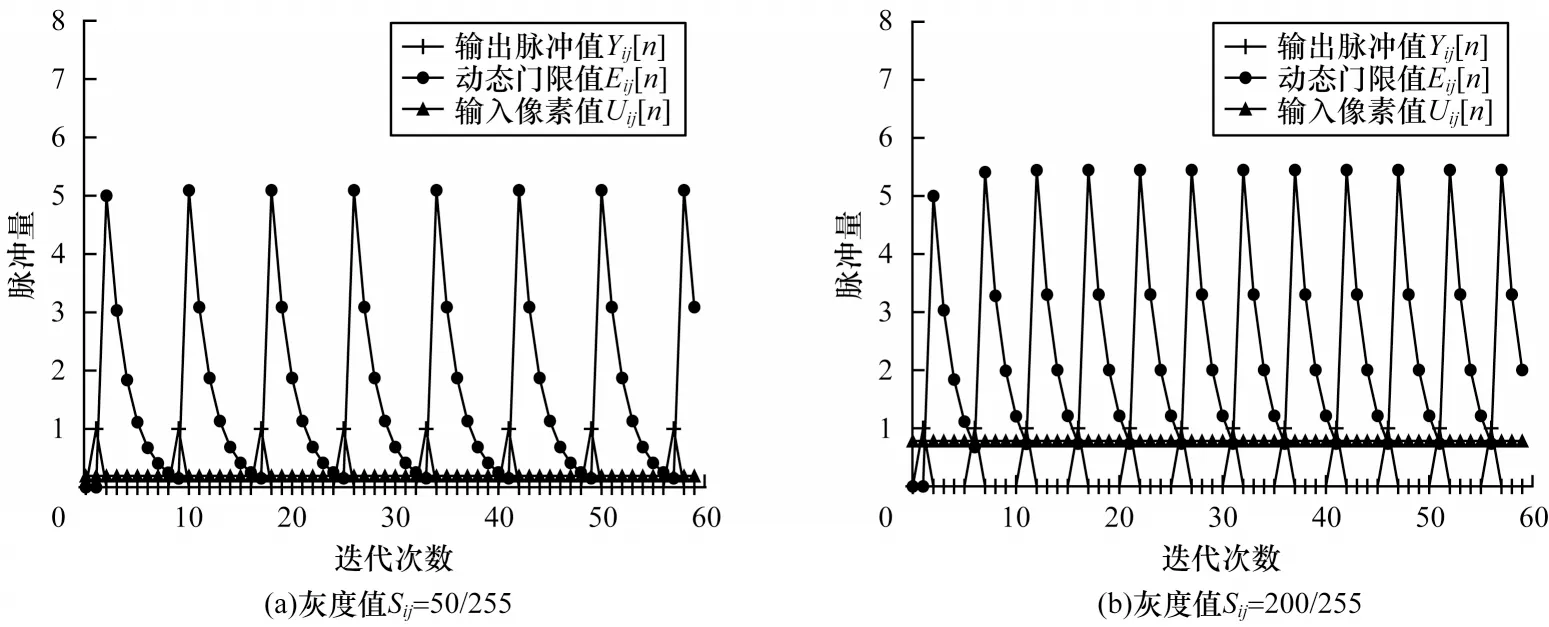
图2 动态门限和点火时刻的变化Fig.2 Change of dynamic threshold and firing timing

因此，输入值与神经元点火周期和动态门限衰减存在非线性映射关系。为分析这种非线性关系，在单个神经元的一个有效点火周期内建立关系，如式（9）所示：

当单个神经元的输入值与动态门限最小值相等时，神经元发生点火。由式（2）可知，动态门限的最大值是脉冲点火时刻后下一次的门限值，Eijmax=+vE，最小值为Eijmin=Sij，设两次脉冲点火时刻的间隔为I，则由式（9）可得式（10）：

间隔I如式（11）所示：

脉冲发放间隔应满足I>0，由此可得vE>(1-)Sijmax。其中：Sijmax表示输入最大值。当输入的最大值与vE和aE满足以上关系时，所有的输入都能表现出良好的脉冲周期发放特性。由脉冲发放间隔得到脉冲发放周期，如式（12）所示：

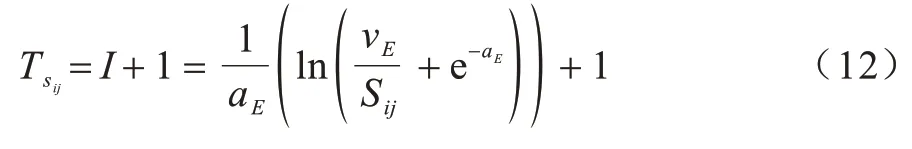
不同输入Sij的点火周期都为正整数，同样的引入ceil 向上取整函数。因此，无耦合PCNN 的实际脉冲发放周期近似为：

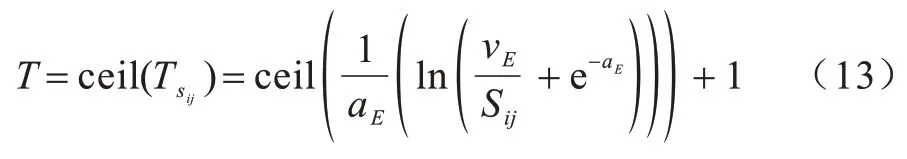
无耦合PCNN 在得到能够反映实际脉冲发放的周期后，脉冲发放时刻如式（14）所示：

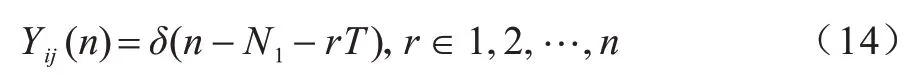
其中：单位冲激函数δ(n)为脉冲发放；N1为第1 次有效点火时刻；r为正整数。

2.2.2 脉冲发放频率与参数影响分析

由脉冲发放时刻方程可知，无耦合PCNN 脉冲点火具有周期性，而周期为N的序列可展开成离散傅里叶级数（Discrete Fourier Series，DFS）。因此，在一个周期内对脉冲发放时刻式（14）进行傅里叶级数展开，如式（15）所示：

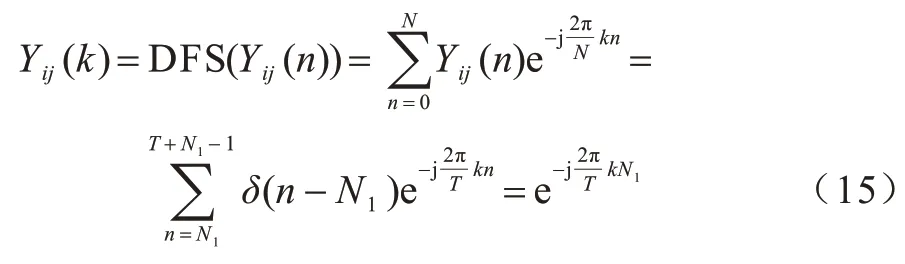
本文对脉冲发放时刻的傅里叶级数表达式进行傅里叶变换（Fourier Transform，FT），可得其脉冲发放频率表达式，如式（16）所示：

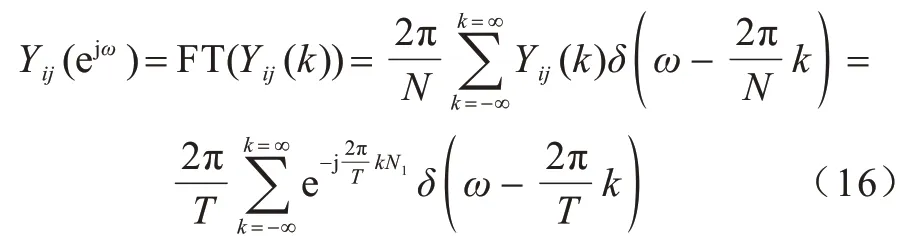
幅值谱函数如式（17）所示：

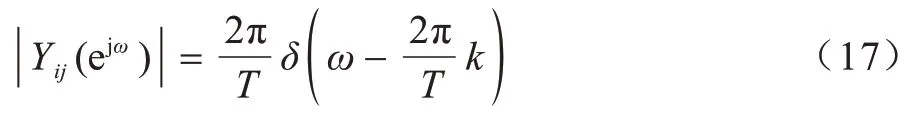
由式（17）可知，无耦合PCNN 的脉冲发放幅值谱是由一系列幅值为和间隔为的冲击序列构成。当选取输 入Sij=20/255 时，ω∈(0，π)范围幅频特性随参数的aE和vE变化趋势如图3 和图4所示。根据离散周期信号频谱特性可知，频域谱线越密，时域脉冲周期越大，频域谱线越疏，时域脉冲周期越小。从图3 和图4 可以看出，参数变化不会引起脉冲发放频谱函数幅值的变化。但是参数aE的增大使得脉冲发放频谱函数的谱线间隔增大，从而增大脉冲点火时刻周期。参数vE的增大反而使得脉冲发放频谱函数的谱线间隔变小，脉冲点火时刻周期减小。

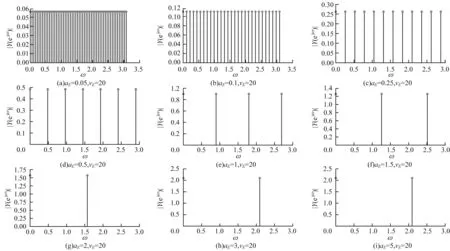
图3 参数aE 增大对脉冲发放幅频特性的影响Fig.3 Influence of parameters aE increase on the amplitude-frequency characteristic of pulse firing

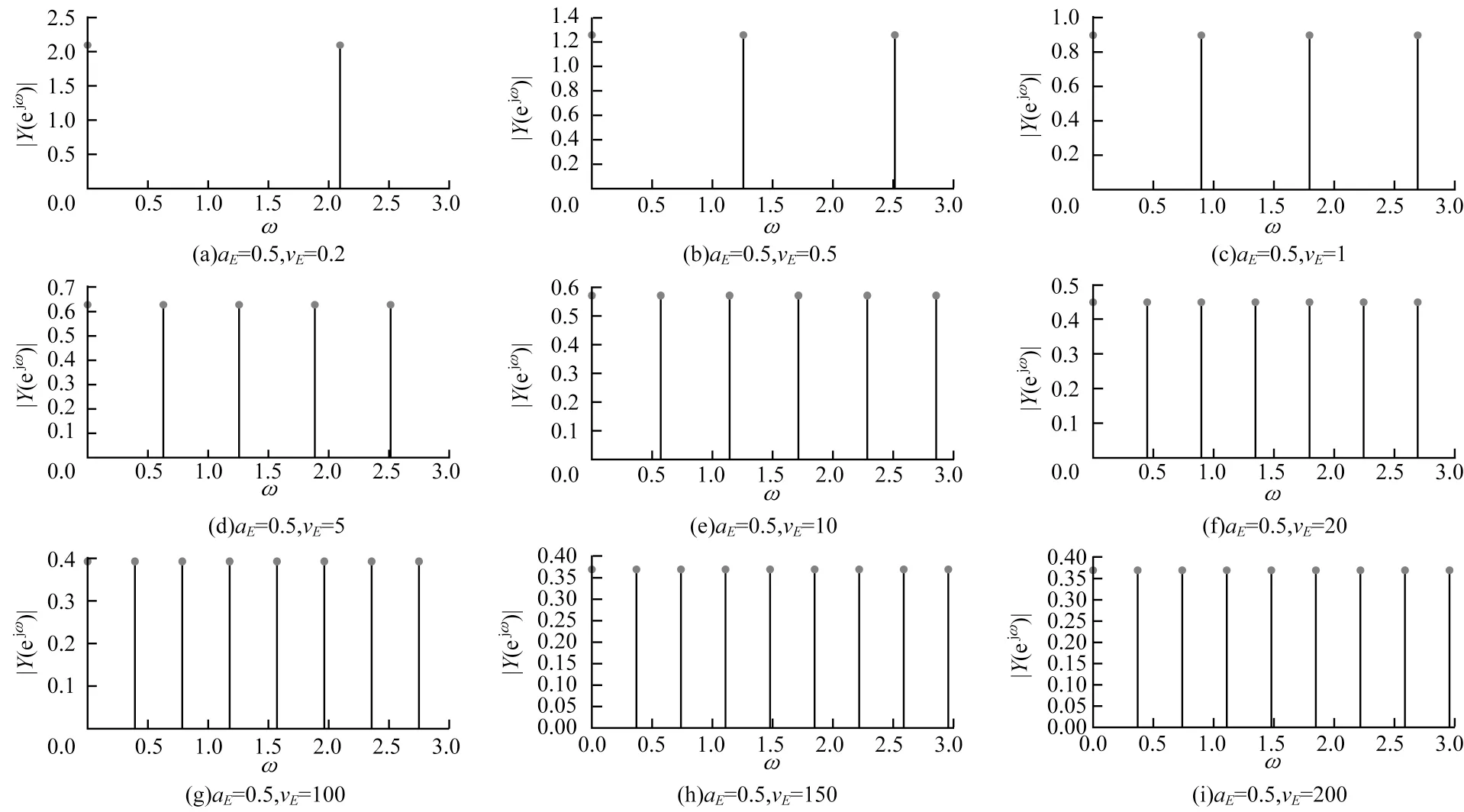
图4 参数vE 增大对脉冲发放幅频特性的影响Fig.4 Influence of parameters vE increase on the amplitude-frequency characteristic of pulse firing

因此，在无耦合PCNN 模型中，参数aE的增大使得脉冲发放时刻周期变小，参数vE的增大会使得脉冲发放时刻周期变大，但不影响脉冲发放的强度。

2.2.3 网络动态门限衰减频率与参数影响分析

动态门限子系统是一个衰减系统，因此将该子系统的输出动态变量Eij(n)的频率称为动态门限衰减频率。动态门限衰减频率与脉冲发放频率存在以下关系，如式（18）所示：

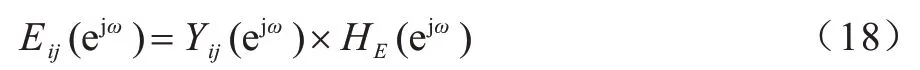
由于式中HE(ejω)和Yij(ejω)已由式（7）和式（15）给出，因此动态衰减频率的频域方程如式（19）所示：

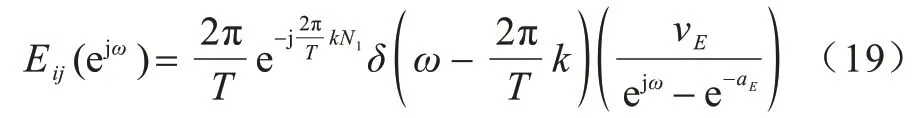
频谱函数如式（20）所示：

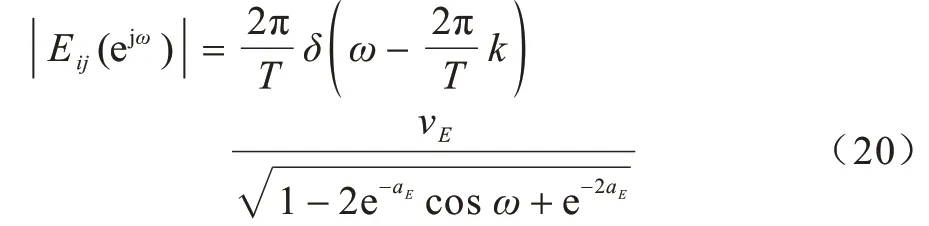
当选取输入Sij=20/255 时，参数aE和vE增大在ω∈(0，π)范围幅频特性随参数变化趋势如图5 和图6所示。

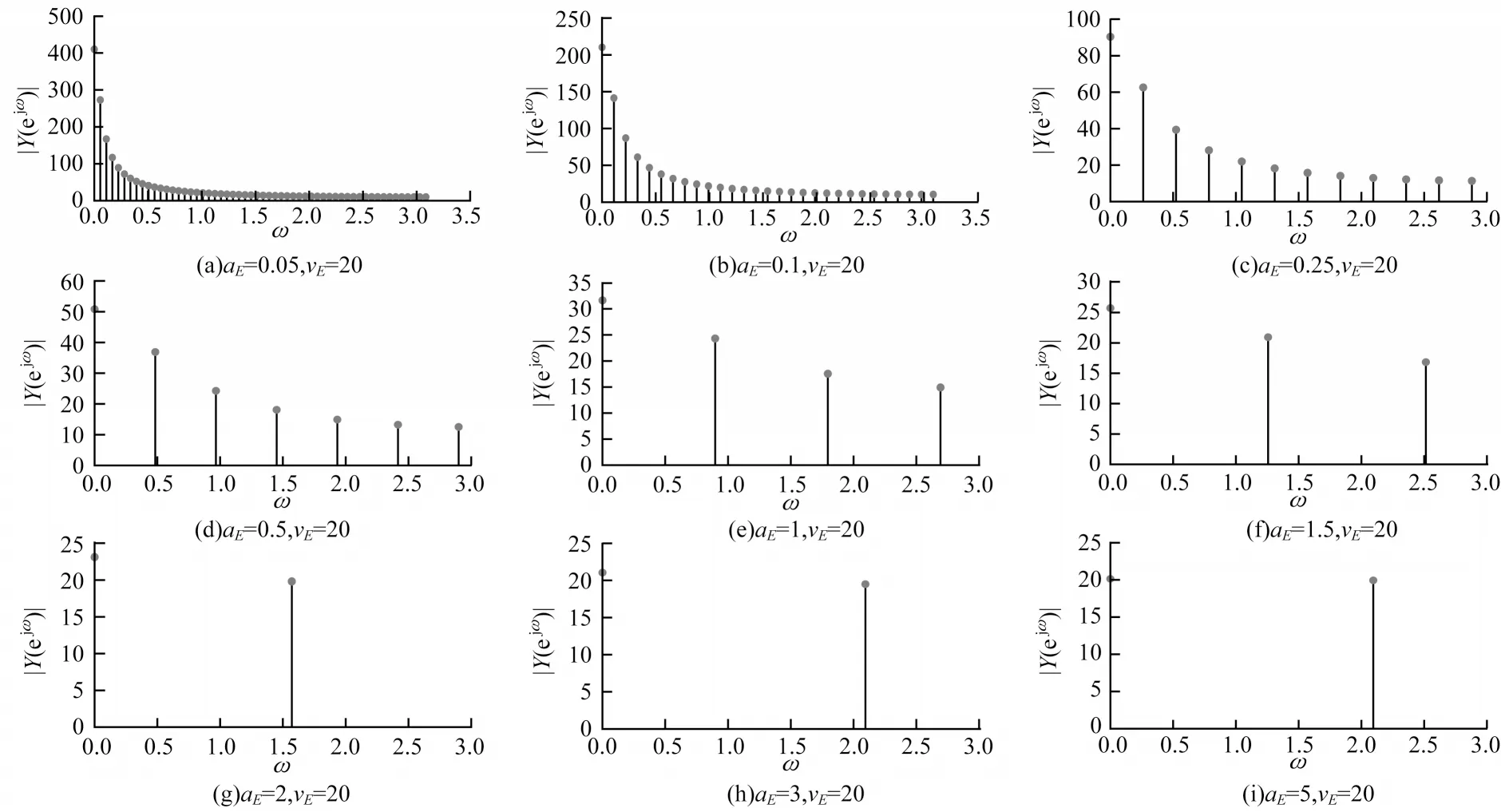
图5 aE 增大对动态门限幅频特性的影响Fig.5 Influence of parameters aE increase on the amplitude-frequency characteristic of dynamic threshold

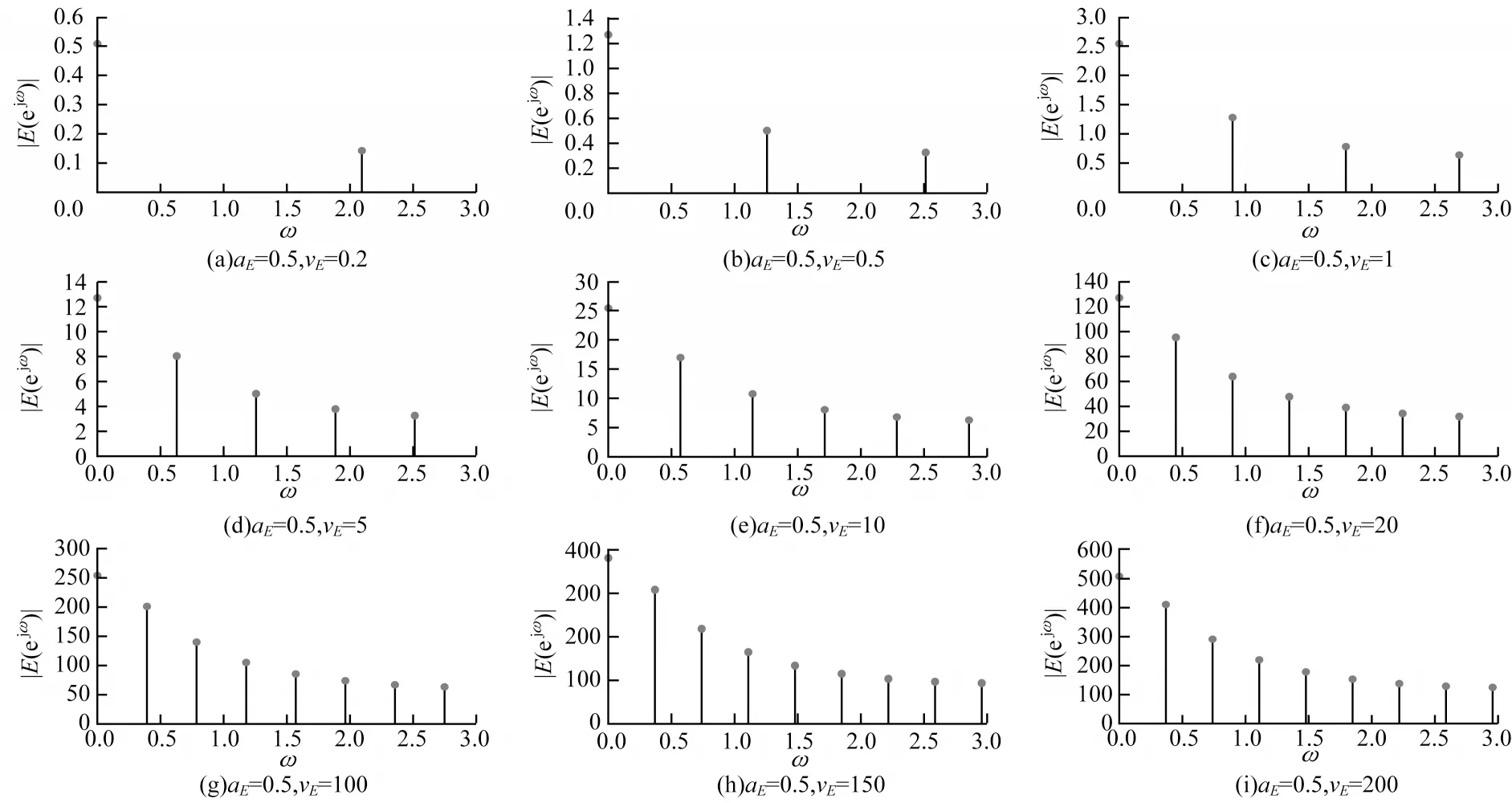
图6 vE 增大对动态门限幅频特性的影响Fig.6 Influence of parameters vE increase on the amplitude-frequency characteristic of dynamic threshold

从式（20）可知，动态门限幅频函数|Eij(ejω)|的频谱谱线间隔与脉冲发放频谱函数的谱线间隔相同，参数对动态门限周期与脉冲发放周期的影响程度相同。从图5 和图6 可以看出，与脉冲发放频谱相比，随着参数aE的增大，动态门限幅频函数的频谱主要由高频分量组成，使得动态门限的衰减频率变大，衰减速度变快。参数vE的增大反而会使得动态门限幅频函数的频谱主要由低频分量组成，动态门限Eij(n)的衰减频率变低。

因此，在无耦合PCNN 模型中，参数aE和参数vE的变化会影响动态门限衰减周期及动态门限衰减频率的高低。

3 实验仿真与验证

本文通过式（7）、式（16）和式（19）描述了无耦合PCNN 模型的频域特性，通过分析参数对无耦合PCNN 模型频域特性的影响，得出参数影响网络运行的结论。在主频2.8 GHz（双核），内存12 GB 的计算机上利用Python3.8 平台完成数值模拟实验，验证了无耦合PCNN 频域相关公式推导及理论分析结论的正确性。

3.1 实际网络脉冲发放时刻

为验证对脉冲发放时刻推导的正确性，本文构建一幅灰度值已知的人工测试灰度图与灰度值，如图7所示。

图7 人工测试灰度图与灰度值Fig.7 Gray scale image of manual test and gray scale value

当网络参数aE=0.9，vE=15 时，无耦合PCNN 实际迭代过程如图8 所示。从图8 可以看出，第1 次迭代为网络的无效点火时刻，之后的各次点火均为有效点火。灰度值在110～250 之间的像素第1 次有效点火时刻为第6 次迭代，点火周期T=5。灰度值在50～100 之间的像素第1 次有效点火时刻为第7 次迭代，点火周期T=6。灰度值在20～40 之间的像素第1 次有效点火时刻为第8 次迭代，点火周期T=7。灰度值为10 的像素第1 次有效点火时刻为第9 次迭代，点火周期T=8。根据第1 次点火公式（4）可计算出各像素第1 次有效点火时刻，根据点火周期公式（13）可计算出各像素点火周期。不同像素的第1 次有效点火时刻和点火周期对比如图9 所示。从图9可以看出，本文所推导公式的脉冲发放过程与人工测试图实际迭代过程相一致。

图8 人工测试图的迭代过程Fig.8 Iterative process of manual test image

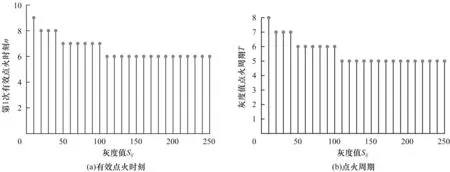
图9 不同像素第1 次有效点火时刻和点火周期Fig.9 The first effective firing time and firing cycle of different pixels

3.2 实际网络参数对脉冲发放与动态门限的影响

本文分别选取灰度值Sij=10/255，Sij=110/255作为对网络中动态变量Yij(n)受参数影响的观测对象。当网络迭代第60次时，其神经元脉冲发放过程如图10所示。从图10 可以看出：在灰度值Sij相同的情况下，保持参数vE=15 不变，aE从0.5 增大到0.9 会使得网络脉冲发放时刻周期变小；保持参数aE=0.5 不变，vE从15 增大到30 使得网络脉冲发放时刻周期变大。因此，在实际的脉冲发放过程中，参数对脉冲发放频率的影响与理论推导分析相一致。

本文分别选取灰度值Sij=10/255，Sij=110/255作为网络中动态变量Eij(n)受参数影响分析的观测对象。当网络迭代第60 次时，不同灰度值下网络实际动态门限变化过程如图11 所示。从图11 可以看出：在输入Sij相同的情况下，保持参数vE=15 不变，aE从0.5 增大到0.9，使得动态门限Eij(n)衰减变快，衰减周期变小；保持参数aE=0.5 不变，vE从15增大到30，使得动态门限Eij(n)的幅值增益变大，衰减变慢，衰减周期变大。因此，动态变量Eij(n)的迭代过程与之前分析结果一致。

4 结束语

本文分析了无耦合PCNN 的频域特性。通过对无耦合PCNN 动态门限子系统进行分析，得出动态门限子系统稳定的条件，确定参数的取值范围，并指出动态门限子系统具有低通特性。同时分析单个神经元的脉冲发放频率特性和动态阈值频域特性，明确参数对网络动态频域的影响。仿真实验结果验证理论分析结论的正确性。后续将从图像特性角度分析图像统计特性对网络参数的影响，设计无耦合PCNN 模型用于图像分割时的参数自适应设置方法，使无耦合PCNN 模型广泛应用于图像处理领域。