拟单层覆盖粗糙集中近似集的增量更新算法

吴正江，张亚宁，张 真，梅秋雨，杨 天

（河南理工大学计算机科学与技术学院，河南焦作 454003）

0 概述

经典的粗糙集［1］在没有任何先验知识的情况下，通过上下近似集表示某个确定的概念，能够处理具有不确定性、不一致性等特点的数据集。粗糙集理论广泛应用于数据挖掘［2］、推荐系统［3］、工业控制系统［4-5］等领域。

信息系统可能伴有部分缺失值或集值。研究人员提出了容差关系［6］、非对称相似关系［7］、限制性容差关系［8］、最大相容类［9］等二元关系代替不可区分关系，使得泛化的粗糙集模型能够处理集值信息系统。文献［10-11］提出拟单层覆盖粗糙集界于一般覆盖与划分之间，是一个特殊的邻域系统。近似质量是衡量一个模型的标准，文献［12］将拟单层覆盖粗糙集应用于集值信息系统中，并在真实数据集上进行实验，证明了该模型在近似质量和计算效率方面均优于容差关系、非对称相似关系、限制性容差关系以及最大相容类，但是该模型无法应用于动态集值信息系统。

随着时间的推移，信息系统也会持续不断地发生变化。求解近似集的效率将直接影响规则提取和属性约简的效率。当信息系统发生改变时，快速获取更新系统中的近似集成为亟待解决的难题。

增量学习是指充分利用已知的信息并且避免从头开始计算，从而达到提升计算效率的目的。将增量学习灵活运用于动态信息系统中近似集的求解可以显著提升其计算效率。信息系统结构的动态变化方式有属性集的变化［13-15］、属性值的变化［16-17］以及对象集的变化。关于对象集发生变化的情况，文献［18］基于模糊优势邻域粗糙集提出动态区间值有序数据的增量特征选择方法。根据云平台下的并行模型MapReduce，文献［19］提出经典粗糙集的并行增量算法，用于更新大规模数据的近似集。当对象批量发生变化时，文献［20］提出一种邻域决策粗糙集模型的增量式更新算法。针对混合型信息系统，文献［21］提出基于邻域决策粗糙集矩阵方法的增量式更新算法。文献［22］提出邻域多粒度粗糙集模型的矩阵化方法并设计了相应的增量更新方法，用于更新正域、负域及其边界域。文献［23］研究了优势粗糙集模型中动态有序数据的增量属性约简方法。

本文提出拟单层覆盖粗糙集中近似集的增量更新算法。当一个对象集添加至原始系统时或一个对象集从原始系统移除时，通过分析拟单层覆盖集中信息单元的变化情况，根据信息单元的变化对各近似集可靠单元和争议单元的相关可靠单元集的影响，设计相应的更新算法。在此基础上，通过计算更新系统中各近似集的最终结果，从而提高近似集的计算效率。

1 基本概念

集值信息系统S=(U，A，V，f)是一个四元组。其中：U是一个非空有限的对象集，称为论域；A是有限的属性集；V为属性的值域且是从U×A到V的集值映射。

定义1令S=(U，A，V，f)为集值信息系统，其中A=(a1，a2，…，an)。对象x∈U的信息解释是一个集值向量。表达式=，其中f(x，ai)是集合。

定义2令S=(U，A，V，f)为集值信息系统。是S上的一个信息单元，且x∈Cellx，。如果中的任意值均为单值，则该信息单元被称为可靠单元。如果中存在集值，则该信息单元被称为争议单元。Cellc的相关可靠单元集记为RS(Cellc)，其中RS(Cellc)=(Cellr∈RC|∀ai∈A，x∈Cellx，y∈Celly，f(x，ai)⊆f(y，ai))。

可靠单元和争议单元分别记为Cellr和Cellc，并且所有可靠元和争议元的集合分别记为RC 和CC。

定理1令S=(U，A，V，f)为集值信息系统。RC和CC 分别包含S中所有的可靠单元和争议单元。对应任意X⊆U，S上X的DA0 和DE0 近似集如下：

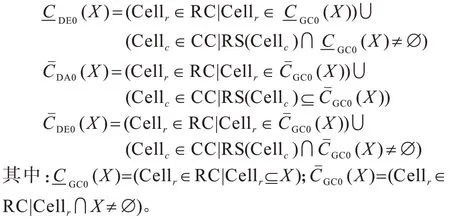
2 近似集的增量更新

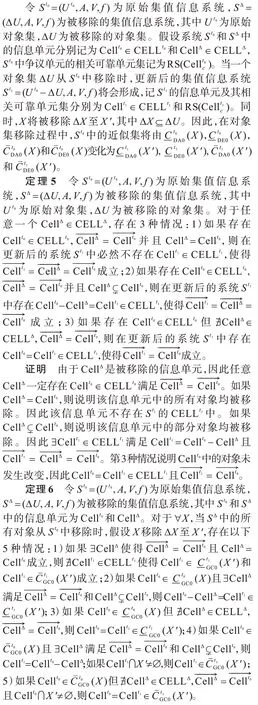
当论域发生变化时，拟单层覆盖粗糙集中的近似集也会发生变化。传统的静态方法将从头开始计算近似集，会浪费大量的时间。本文提出当对象集变化时拟单层覆盖粗糙集的增量更新方法，充分利用已知的计算结果，达到提高计算效率的目的。

2.1 对象增加时近似集动态更新

2.2 对象移除时近似集动态更新

3 本文算法

本文设计增量更新算法，算法1 为静态算法，算法2 和算法3 分别为对象集增加时和减少时的增量更新算法。

3.1 静态算法

在定义2 和定理1 的理论基础上，本文设计相应的静态算法。

3.2 对象集添加时近似集的增量更新算法

当原始系统中添加一个对象集时，根据2.1 节提出的方法设计相应的增量更新算法。

3.3 对象集移除时近似集的增量更新算法

当原始系统中移除一个对象集时，根据2.2 节提出的方法设计相应的增量更新算法。

本文通过对比静态算法和两个增量算法的时间复杂度可知，无论对象集被添加还是被移除，增量算法的时间复杂度总低于静态算法的时间复杂度。

4 实验结果与分析

本文通过在真实数据集上的一系列实验验证增量算法的有效性。在计算结果保持一致的前提下，本文计算拟单层覆盖粗糙集中近似集所消耗的时间，对比静态算法和增量算法的效率。

本文实验分为对象添加和对象移除两种情况。这两种情况下的对比实验均在UCI 数据集上进行。数据集的具体描述如表1 所示。

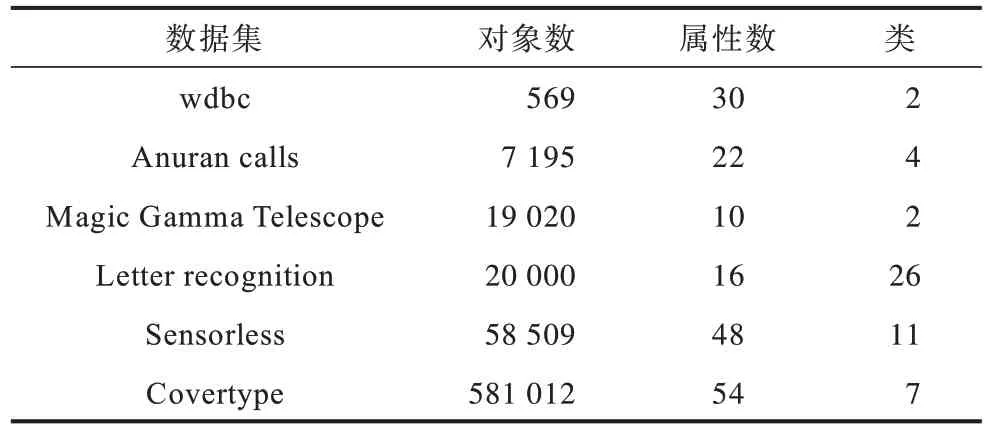
表1 数据集描述Table 1 Data sets description

本文对数据集进行预处理形成对应的集值信息系统，分别计算每个属性的最小值、最大值、平均数和中位数，将其从小到大排列产生3 个间隔。如果该列的某个属性值位于第1 个间隔，则该属性值对应于单值记录。如果其位于第3 个间隔，则该属性值对应于与前者不同的单值记录，否则该值对应于前两者组成的集值记录。

实验环境的操作系统为Windows 10，CPU 为Intel®CoreTMi7-9750H，内存为16 GB。本文使用Java 编程语言在IDEA 平台上实现静态和增量算法，其中Java 虚拟机版本为JVM 1.8。

当对象集发生变化时，本文在保持原始数据集包含对象数不变的前提下，依次增加发生变化（被添加到原始系统或从原始系统中移除）的对象数，对比静态算法和增量算法的计算时间，以验证增量理论和对应算法的有效性。

对于一个对象集被添加至原始集值信息系统的情况，本文对数据集进行如下处理：1）取出前50%的对象作为原始数据；2）将后50%的对象平均划分为10 份；3）依次将10%，20%，…，100%添加至原始数据。针对算法1 和算法2，本文使用以上产生的10 组添加对象数不同的数据进行实验。在不同的数据集上，当对象增加时算法1 和算法2 计算时间的对比如图1 所示。

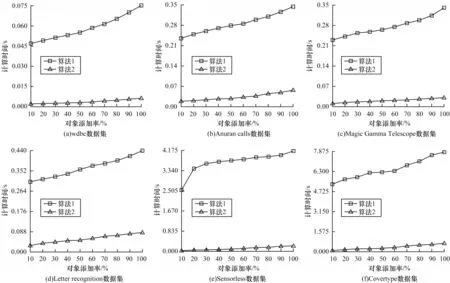
图1 当对象增加时算法1 和算法2 的计算时间对比Fig.1 Computation time comparison of algorithm 1 and algorithm 2 when objects are added

从图1 可以看出，随着添加至原始数据集中对象数目的增加，算法1 和算法2 的计算时间都呈增加趋势，但算法1 对应曲线的斜率更大，并且计算时间比算法2 多。因此，算法1 的效率低于算法2。当数据集中包含对象增加时，信息单元（可靠单元和争议单元）的数目也会随之增加。根据算法1 和算法2 的时间复杂度可知，2 个算法随着对象集的增加所需的计算时间也会增加，即图1 的结果也与时间复杂度的分析保持一致。

当对象添加率为10%、50%和100%时，静态算法1和增量算法2 计算近似集所需运行时间的比值如表2 所示。从表2 可以看出，随着对象添加率的增加，算法1 和算法运行时间的比值越来越小。在Sensorless 数据集上，当对象添加率达到100%时，算法1 的执行时间为4.155 s，而算法2 仅需0.224 s，前者仍是后者的18 倍。

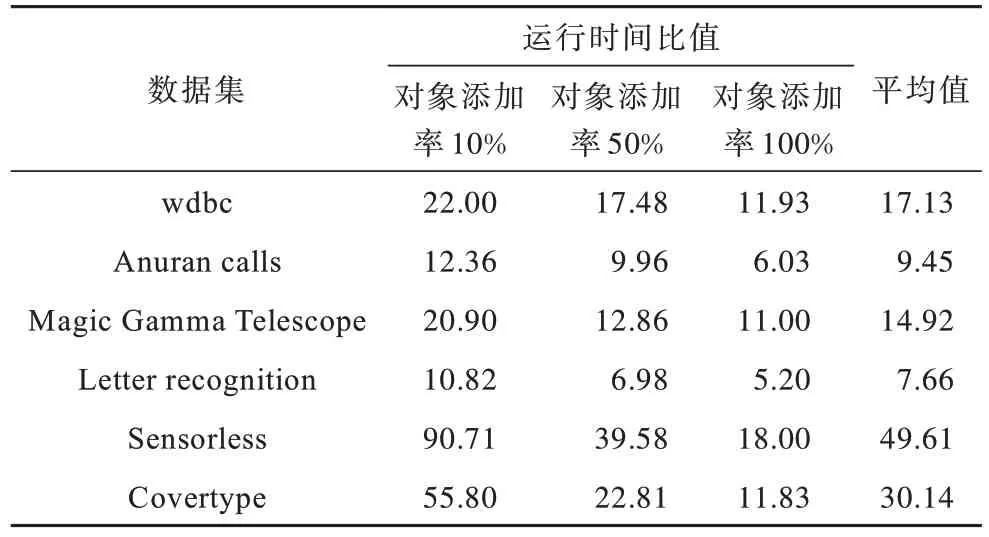
表2 算法1 与算法2 运行时间的比值Table 2 Running time ratio of algorithm 1 and algorithm 2

对于一个对象集从原始集值信息系统中移除的情况，本文对数据集进行如下处理：1）将完整的数据集作为原始数据；2）将后50%的对象平均划分为10 份；3）依次将10%，20%，…，100%从原始数据中移除。针对算法1 和算法3，本文使用以上产生的10 组移除对象数中不同的数据进行实验。在不同的数据集上，当对象移除率增加时算法1 和算法3 的计算时间对比如图2 所示。从图2 可以看出，随着移除对象的增加，算法1 呈下降趋势，而算法3 呈上升趋势，但是算法3 的曲线总在算法1 对应曲线的下方。因此，当论域中部分对象集移除时算法3 的效率更高。

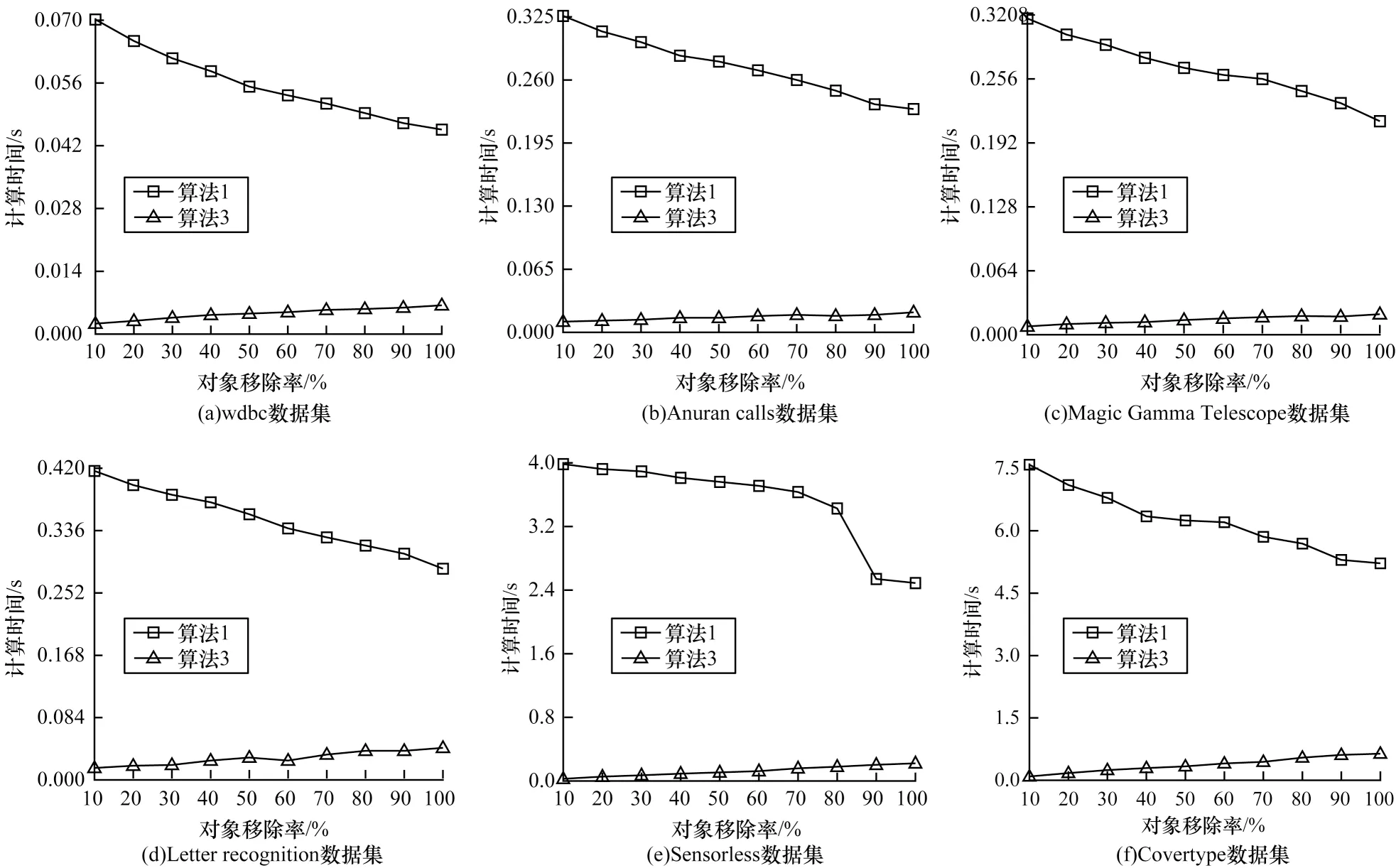
图2 当对象移除时算法1 和算法3 的计算时间对比Fig.2 Computation time comparison of algorithm 1 and algorithm 3 when objects are removed

当对象移除率为10%、50%和100%时，静态算法1和增量算法3 计算所需运行时间的比值如表3 所示。

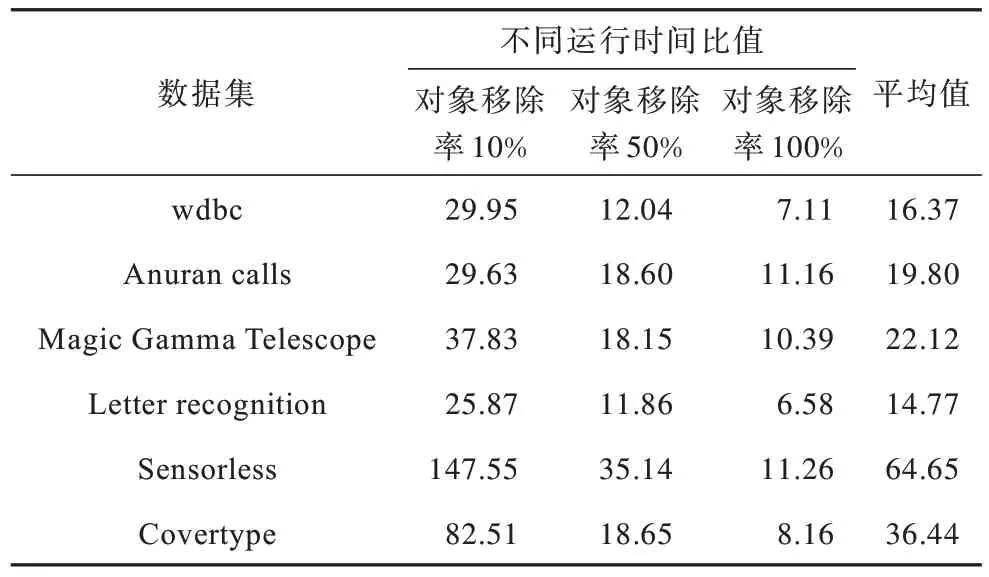
表3 算法1与算法3运行时间的比值Table 3 Running time ratio of algorithm 1 and algorithm 3

从表3可以看出，当对象移除率增加时，静态算法1和增量算法3 计算所需运行时间的比值越来越小。在Sensorless 数据集上，当对象移除率达到100%时，算法1 的执行时间为2.489 s，而算法3 仅需0.221 s，前者是后者的11.26 倍。

表4 在不同对象移除率下的结果Table 4 Result of under different object removal ratio

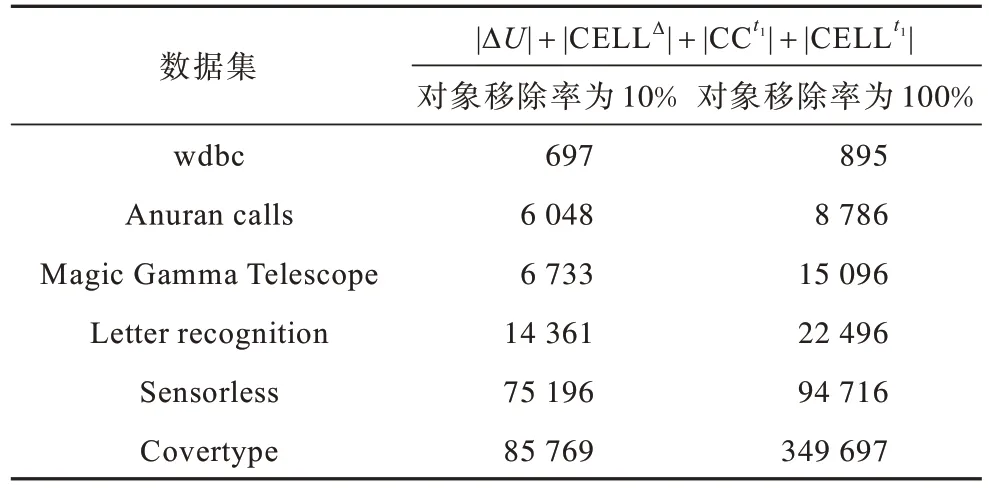
表4 在不同对象移除率下的结果Table 4 Result of under different object removal ratio

5 结束语

因集值信息系统中的对象集随时间的推移而增加或移除，导致拟单层覆盖粗糙集中的近似集发生变化。本文结合增量学习与拟单层覆盖粗糙集，提出近似集的增量更新算法。通过设计信息单元、可靠单元和争议单元的更新方法，以达到提高计算效率的目的。构建与更新算法相对应的增量算法，并分析其时间复杂度。在UCI 数据集上进行实验，结果表明，当对象集发生变化时，本文算法相较于静态算法的近似集计算效率高。下一步将拟单层覆盖粗糙集增量更新算法与大数据框架相结合，并对本文增量更新算法的并行化问题进行研究，使其能够实时处理海量数据。