基于粒计算的支持向量数据描述分类方法
方 宇,曹雪梅,杨 梅,王 轩,闵 帆
(1.西南石油大学计算机科学学院,成都 610500;2.西南石油大学网络与信息化中心,成都 610500)
引 言
分类问题作为一项重要的任务,在机器学习、模式识别和数据挖掘领域有着广泛的应用[1⁃2]。在分类问题的模型构造上面,通常分为多分类方法和单分类方法,支持向量数据描述(Support vector data description,SVDD)[3]作为单分类方法的研究热点,其理论源于支持向量机[4](Support vector machine,SVM),特别适用于分类[5]、异常检测[6]、机械性能评估[7]、质量过程监测[8]和医学诊断[9]等领域。传统的SVDD 是通过在高维特征空间中训练最小超球,以此确定目标对象决策边界,从而达到分类和异常检测的目的。优化SVDD 的决策边界是SVDD 理论的研究重点,众多学者相继提出了各种优化方法。Tax 等[10]使用核主成分分析对样本做预处理,保证所有维的数据分布方差一致,从而得到更优的分类决策边界;Hoffmman 等[11]使用特征空间映射与主成分投影的差作为新量度,使得SVDD 的性能有显著的提高。但计算核PCA 的代价、提取核矩阵特征值的代价均较高;Sadeghi 等[12]使用模糊集验证度加权,使决策边界侧重关系密切的数据。Cha 等[13]使用密度加权,以增加对密集数据误分类的惩罚;在算法层面,Peng 等[14]提出了E⁃SVDD 算法提高对象预测速度。Kim 等[15]提出了深度学习神经网络模型用于改善SVDD 的过拟合问题。在多分类方面,Huang 等[16]提出了SVDD 两类分类器的算法,Zhu等[17]提出了基于推广能力测度的多类SVDD 模式识别方法。
以上针对SVDD 的优化方法均是在一个粒度下求解的分类决策边界,这会存在目标对象未被划分的情况。粒计算[18]是一种高效、可扩展的计算方法,其粒化思想较好地解释了在分析和处理事务中采用自上而下、逐步求精的策略。这种策略在复杂分类问题中的应用优势尤为明显[19]。因此,本文基于粒计算思想,提出一种新分类方法。在该方法中,选择合适的属性重要度排序方法是构建粒的关键。Pawlak 提出的粗糙集理论是一种处理不确定、不精确和不完备数据的有效手段[20]。众多研究者基于它提出了启发式特征选择算法。苗夺谦等[21]提出利用互信息衡量属性重要度的方法。王国胤等[22]设计了一种利用条件熵作为启发式信息函数的特征选择算法。宋桂娟等[23]利用决策属性相对于条件属性的条件熵和互信息的概念,提出了基于信息熵属性约简算法。然而,现有的大多数特征选择方法均是基于决策下近似构造的,这样会导致算法只考虑样本决策一致性的分类信息,而忽略决策分歧的样本提供的分类信息。因此,王长忠等[24]提出了综合考虑决策上下近似的邻域自信息,可以更准确地评估属性重要度。
1 支持向量数据描述
SVDD 的目的是找到目标数据的最佳数据描述[3],即找到包含尽可能多的目标数据的最小超球。假设有数据集{xi,i=1,…,l},其中l为目标类对象个数,SVDD 的目标函数为

式中:R为超球半径;C为平衡超球体积和球外目标数据数量之间的参数;ξi为松弛变量;a为超球中心。如图1 所示,绿色点为目标类数据,黄色点为非目标数据,虚线圆则表示所求最小超球。
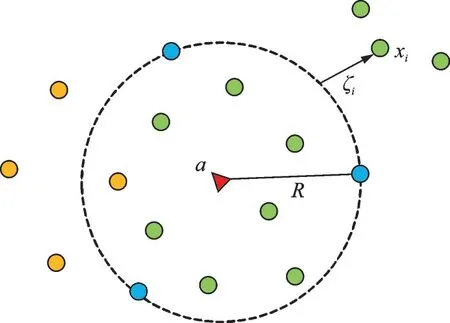
图1 特征空间中的SVDD Fig.1 SVDD in feature space
为了解决这些约束条件下的优化问题,构造了如下拉格朗日函数
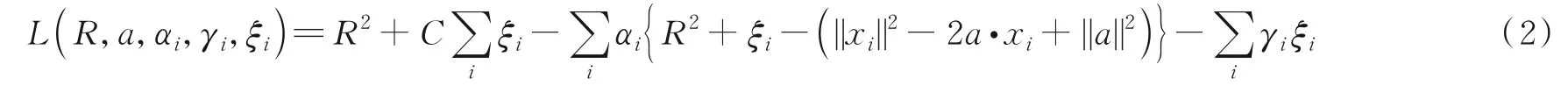
式中:αi≥0,γi≥0 是拉格朗日乘数。为求拉格朗日函数的驻点,将偏导数设为0。
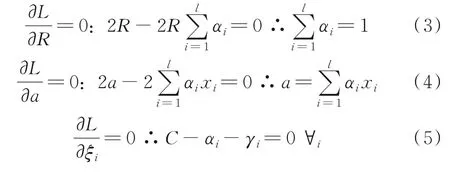
将新的约束式(3,5)代入拉格朗日函数式(2)中,得到如下新的目标函数
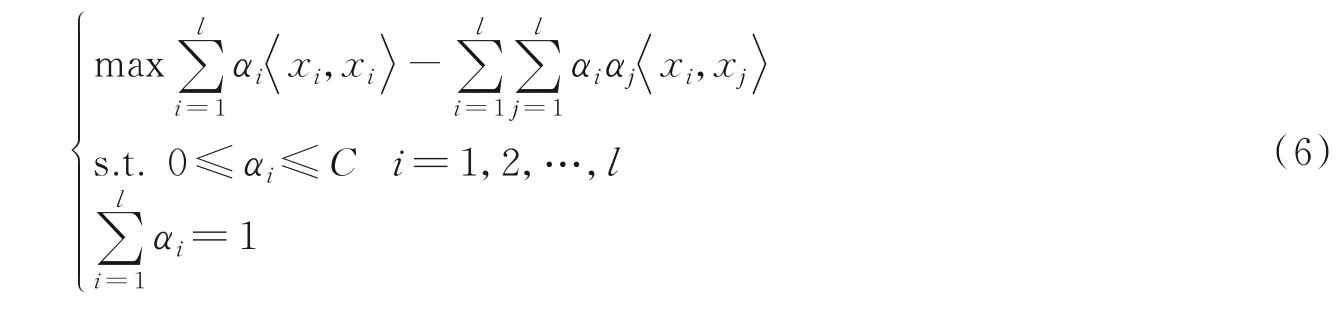
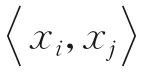
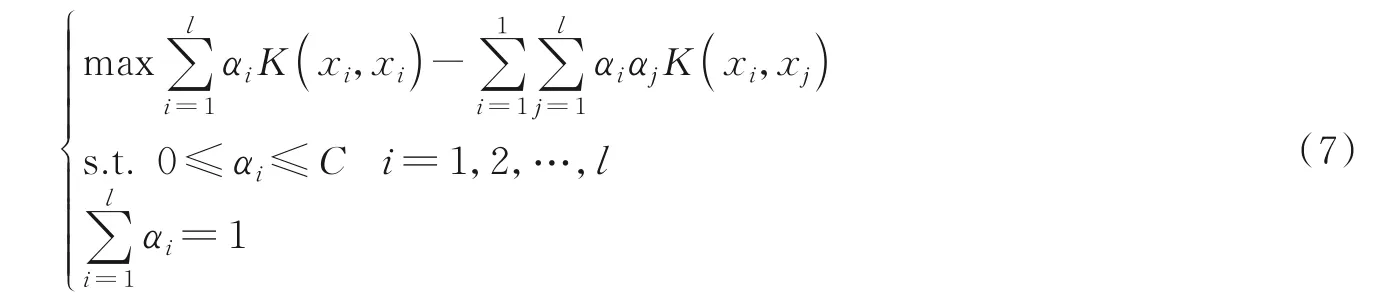
因此,可以根据式(7)计算每个αi的值;再依据任何非零αi的线性组合,即支持向量(Support vectors,SVs)和式(4)来求出最优超球的中心,和式(8)求出超球半径,以此确定最佳的边界描述。SVs 如图1 边界蓝色点所示。
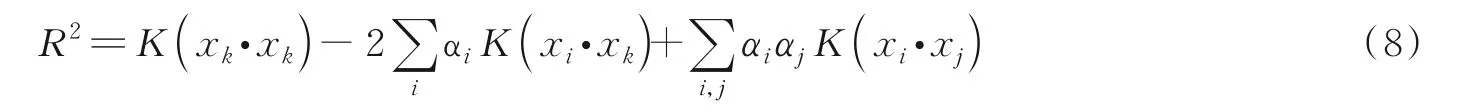
为了判定测试样本z的类别,即z是否在超球体内,需计算样本z到超球中心a的距离,当其距离小于等于超球半径时,即
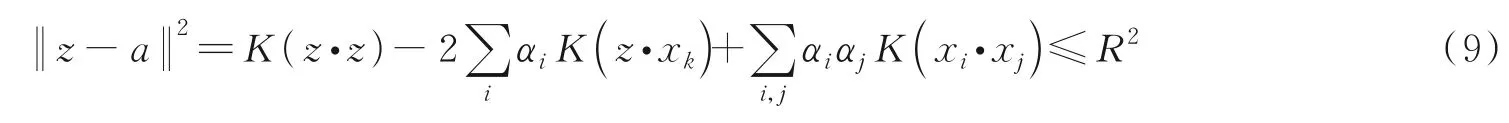
判定样本z为超球内样本;否则为超球外样本。
2 SVDD 粒计算模型
SVDD 粒计算模型分为两个步骤:首先利用邻域自信息计算粒层属性集合,其次根据粒层属性集合构造多粒度超球。本节详细介绍邻域自信息,并给出GrC⁃SVDD 模型构造。
2.1 邻域自信息
邻域粗糙集是处理数据挖掘不确定性的有效方法之一[25],邻域自信息是利用邻域粗糙集理论中的上下近似概念构造的不确定性测度[24],能同时考虑决策上下近似包含的分类信息,准确地刻画属性重要度。
定义1[26]决策表是一个五元组

式中:U为一个非空的有限对象集合;C为条件属性集合;D为决策属性集合;At为属性的非空有限集合;Va为每个属性a∈At的值的集合;Ia为属性a∈At的信息函数。
定义2[24]给定决策表S,B⊆At,dB(x,y)为对象x,y在属性子集B上的欧氏距离,δ为邻域粒度,邻域关系定义为
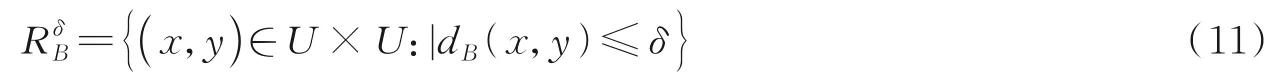
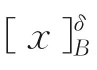

定义4[24]给定决策表S,B⊆At,x∈U,为由B诱导的U上邻域关系,对于任意X⊆U,X的下近似和上近似定义为
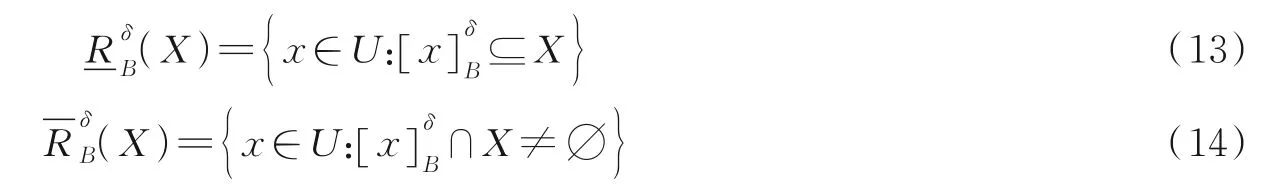
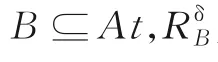

确信决策指标用决策的下近似的基数刻画,表示分类一致的样本数量。可能决策指标用决策的上近似的基数刻画,表示可能属于该决策类的样本数量。
定义6[24]给定决策表S,U/D={E1,E2,…,Er},B⊆At,决策自信息IB(Ek)和决策信息系统的决策自信息IB(D)定义为
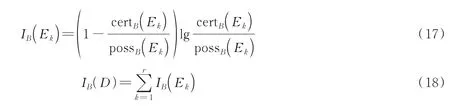
例1表1 为iris 数据集决策表S,其中At={a1,a2,a3,a4}为属性集,U={x1,x2,…,xn}为对象集,D={1,2,3}为决策属性集,通过决策属性D将论域U化成3 个等价类E1={x1,x2,…,xi},E2={xi+1,xi+2,…,xl}和E2={xl+1,xl+2,…,xn}。

表1 决策表Table 1 Example of decision table
设定邻域粒度δ=0.33,首先依据式(15,16),计算等价类E1,E2,E3在a1,a2,a3,a4上的确信决策指标和可能决策指标。其次,根据式(18)计算a1,a2,a3,a4的决策自信息,得Ia1(D)=34.54,Ia2(D)=34.54,Ia3(D)=24.48,Ia4(D)=23.46。自信息最小的属性更为重要,所以a4相比其他3 个属性更有利于目标对象边界描述。
2.2 GrC‑SVDD 模型
对信息粒化合理的解释是GrC⁃SVDD 多粒度空间构建的前提。信息粒代表一个U的一个对象子集,它描述了一个系统或问题的子部分。通过聚集相同粒度的信息粒,可以得到一个系统或问题的整体描述[27]。在GrC⁃SVDD 中,粒超球即为信息粒。GrC⁃SVDD 粒化过程可解释为对原始数据在粒层属性集合上求解粒超球的过程。同时,小的粒超球是由大的粒超球细化而来。
定义7给定决策表S,A⊆C,粒超球GB定义为
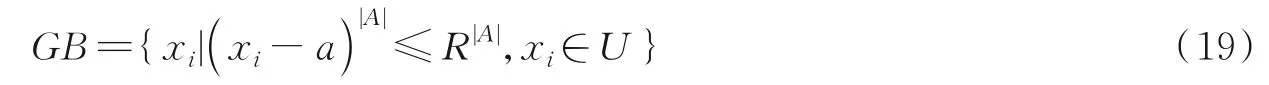
式中:a和R为粒超球中心和半径,分别由式(4,8)计算所得,|A|为属性维度。
定义8给定决策表S,假设有n+1,n≥1 层粒度,在决策表S上的粒化定义为

式中:g(Ai)为某一特定相同粒度的粒超球集合;Ai(1 ≤i≤n)为条件属性的子集,且满足条件A1⊂A2⊂…⊂An⊂An+1。
定义9给定一个粒超球GB,其纯度p定义为

式中:o为该粒超球所有对象个数;n为该粒超球中非目标对象个数,即误包含对象个数。
算法设计如算法1 所示。以表1 为例,第1轮先根据邻域自信息计算每个属性的重要度,然后选出相对最重要的属性作为当前粒层的属性集合F1={a4},分别把等价类E1,E2,E3视为目标数据,在F1上对其进行SVDD 训练,得到每个等价类的粒超球。计算每个粒超球的纯度p,将其与设定的纯度阈值对比,看其是否达到纯度要求,若该粒超球的纯度达到阈值,则其训练结束。如未达到阈值,则需要增添信息,使边界刻画更加清晰。此时在剩余的属性中选择出与a4配合最好的1个属性。即I{a4,ai}(D) (i=1,2,3)最小的集合。经过计算,I{a4,a3}(D)最小,则当前粒层属性集合F2={a4,a3}。利用F2对上一粒层未达到纯度阈值的粒超球进行同样的SVDD 训练和判断,直到所有细化的粒超球都达到纯度阈值或者属性集合F=C时,训练结束。此时,会得到若干达到纯度阈值的粒超球。当有测试样本时,根据式(9)计算样本离每个粒超球的距离,预测其类别与距离最近粒超球一致。
算法1支持向量数据描述的粒计算分类算法
输入:决策表S,邻域粒度参数δ,平衡参数C,高斯核带宽σ,纯度阈值ε。
输出:粒超球集合leaf。
(1)初始化:red=∅,B=C-red,L=U,leaf=∅;/*red 存放当前特征子集,B存放剩余特征,leaf 存放满足条件的粒超球,L存放每个粒层粒超球集合*/
(2)while red ≠C
(3)T=∅;
(4)for eachai∈B
(5)T←red ∪{ai};
(6)根据式(18)计算T的决策自信息IT(D);
(7)end for
(8)找到使IT(D)值最小的属性al;
(9)red ←red ∪{al},B←B-red;
(10)对L求粒超球集合g(red),根据式(22)计算每个粒超球GB的纯度p;
(11)L=g(red)
(12)遍历g(red)中每个粒超球GBi
(13)ifpi>ε
(14)L←L-GBi,跳转至步骤3;
(15)else
(16)leaf=leaf ∪GBi
(17)end if
(18)end for
(19)end while
(20)return leaf
图2 直观地描述了GrC⁃SVDD 整个训练过程,其中黄、红、绿三种颜色对应的点分别表示类别1、类别2和类别3 的样本,黑色虚线为粒超球决策边界,ai和Ri分别是每个粒超球的中心和半径,红色虚线表示粒层间的映射。对于任意数据集U,认为其最开始为粗粒度状态。利用邻域自信息选出粒层1 的属性集合F1作为其特征空间,在这个特征空间上,对该数据集的r个类别的样本分别进行SVDD 训练,最后得到r个粒超球。图2 中的U即为3 个类别,最后得到GB1,GB2和GB3三个粒超球,计算每个粒超球的纯度,发现粒超球GB1达到了纯度阈值,不再继续训练。这表明在特征空间F1中,类别1 在决策边界完全可分。粒超球GB2和GB3未达到纯度阈值,这表明在特征空间F1中,类别2 和类别3 的决策边界描述还需要增添信息。因此,将其映射到特征空间F2中,再次训练。此时,GB2和GB3中只包含类别2 和类别3,只需分别对GB2和GB3中的类别2 和类别3 进行SVDD 训练。得到粒超球GB4,GB5,GB6和GB7,计算其纯度,发现在特征空间F2中,类别2 和类别3 在决策边界上已经完全可分,即达到纯度阈值,整个训练结束。当有测试样本时,计算其到粒超球GB1,GB4,GB5,GB6和GB7的距离,预测其类别为最近粒超球的类别。
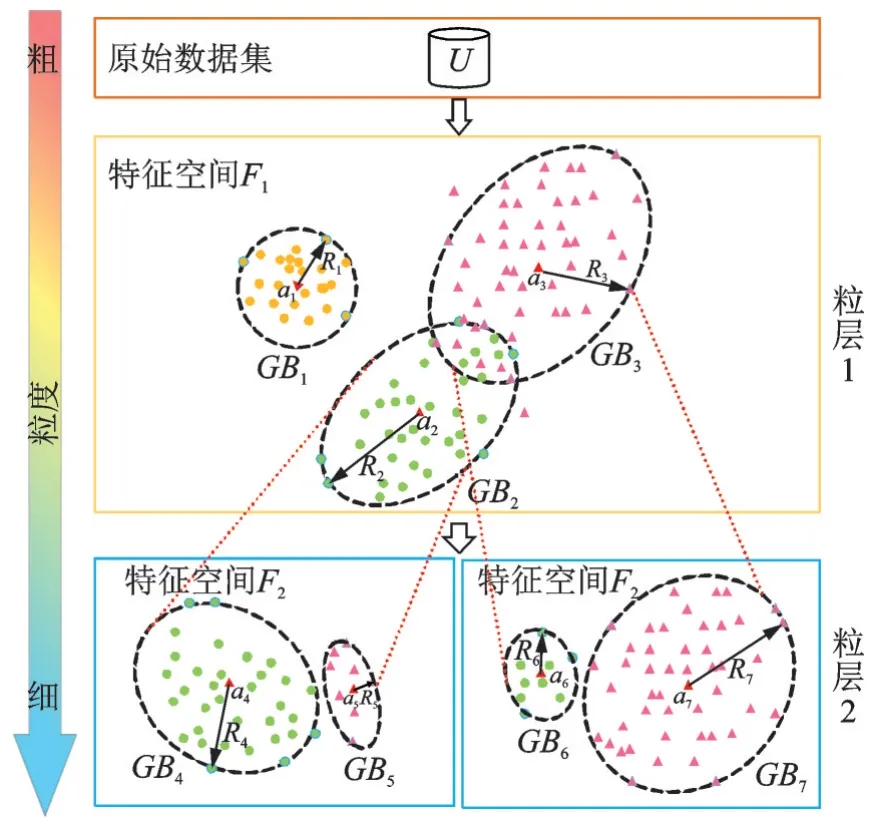
图2 GrC-SVDD 粒化示意图Fig.2 GrC-SVDD granulation diagram
3 实验分析
实验选用10 个UCI 数据集运用于算法的验证,数据具体信息见表2 前4 列。实验采用十折交叉验证,依据精度的大小来评估GrC⁃SVDD 与对比算法的分类性能,精度定义为

式中:N为总数据对象个数;e为误分类个数。为了获得最佳的实验结果,邻域半径δ和纯度阈值ε的设置至关重要。因此,通过讨论参数δ∈[0,1],步长为0.01 和ε∈[0.8,1],步长为0.1,找到每个数据集达到最佳精度时的参数取值。以iris 数据集为例,图3、4 分别显示了GrC⁃SVDD 随邻域半径变化以及纯度阈值变化的分类精度。以此方法找到所有数据集的最优参数设置,详细取值见表2 后两列。平衡参数C设置为1,高斯核带宽σ=1/(n×t),其中n为目标对象个数,t为目标对象标准差。实验环境:操作系统,Windows10,CPU 为AMD4800H,编译环境为Python3.8。
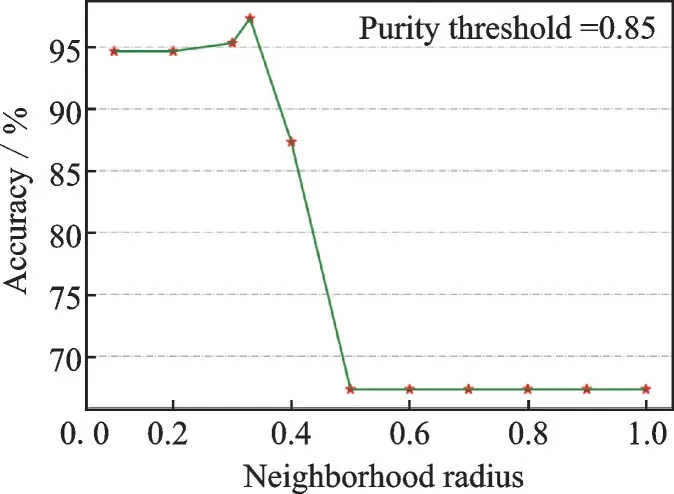
图3 iris 分类精度随邻域半径的变化曲线Fig.3 Variation of classification accuracies with neighborhood radius

图4 iris 分类精度随纯度阈值的变化曲线Fig.4 Variation of classification accuracies with pu⁃rity threshold
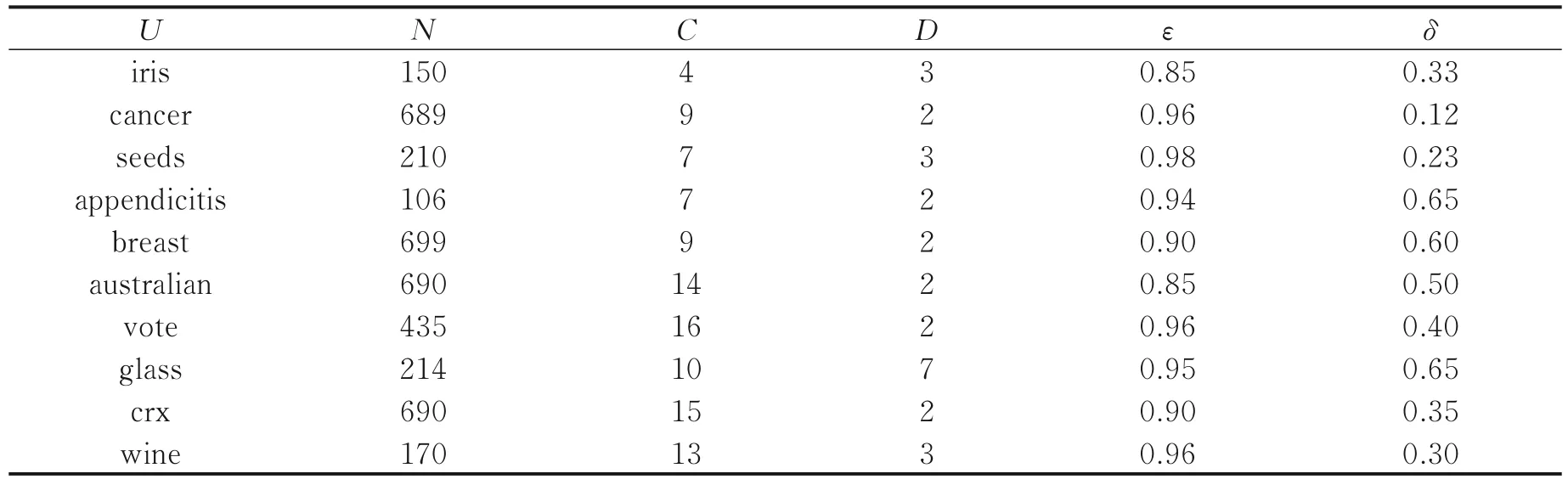
表2 数据集信息Table 2 Information of datasets
GrC⁃SVDD 在粒化的过程中,仅选择了部分属性用于训练,其训练平均使用属性个数如图5 所示。Original 表示数据集原始属性个数,同时是对比算法训练使用的属性个数。橙色表示GrC⁃SVDD 训练所使用的平均属性个数。图中橙色柱条明显矮于蓝色柱条,即GrC⁃SVDD 训练使用属性个数明显少于对比算法。特别是在glass,iris 以 及wine 数据集上,GrC⁃SVDD 仅用了少部分属性进行训练。

图5 原始属性个数和GrC-SVDD 使用属性个数对比Fig.5 Comparison of the number of original attri⁃butes and the number of attributes used by GrC-SVDD
实验对比了5 种分类算法:k近邻(k⁃nearest neigh⁃bor,kNN)[28]、决策树(Decision tree C4.8,J48)[29]、贝叶 斯(Naive Bayesian,NB)[30]、逻辑回归(Logistic re⁃gression,LGR)[31]以及SVDD。实验结果如表3 所示,加粗的数字表示与其他算法相比,在对应数据集上分类效果相对最优。加减的角标为十折交叉验证的精度标准差,表示在不同训练集上精度的波动,即模型的泛化能力。相对比之下,GrC⁃SVDD 分类精度6 次达到最佳,其中在iris 数据集上精度达到97.33%,明显优于其他分类算法。在这10 个数据集上,GrC⁃SVDD 精度Meanrank 为2,位居第一。平均标准差相对最小,即精度波动最小。实验结果充分表明,GrC⁃SVDD 不仅只使用了少量属性训练,而且分类性能较好,模型泛化能力也较强,适应大多数数据集。
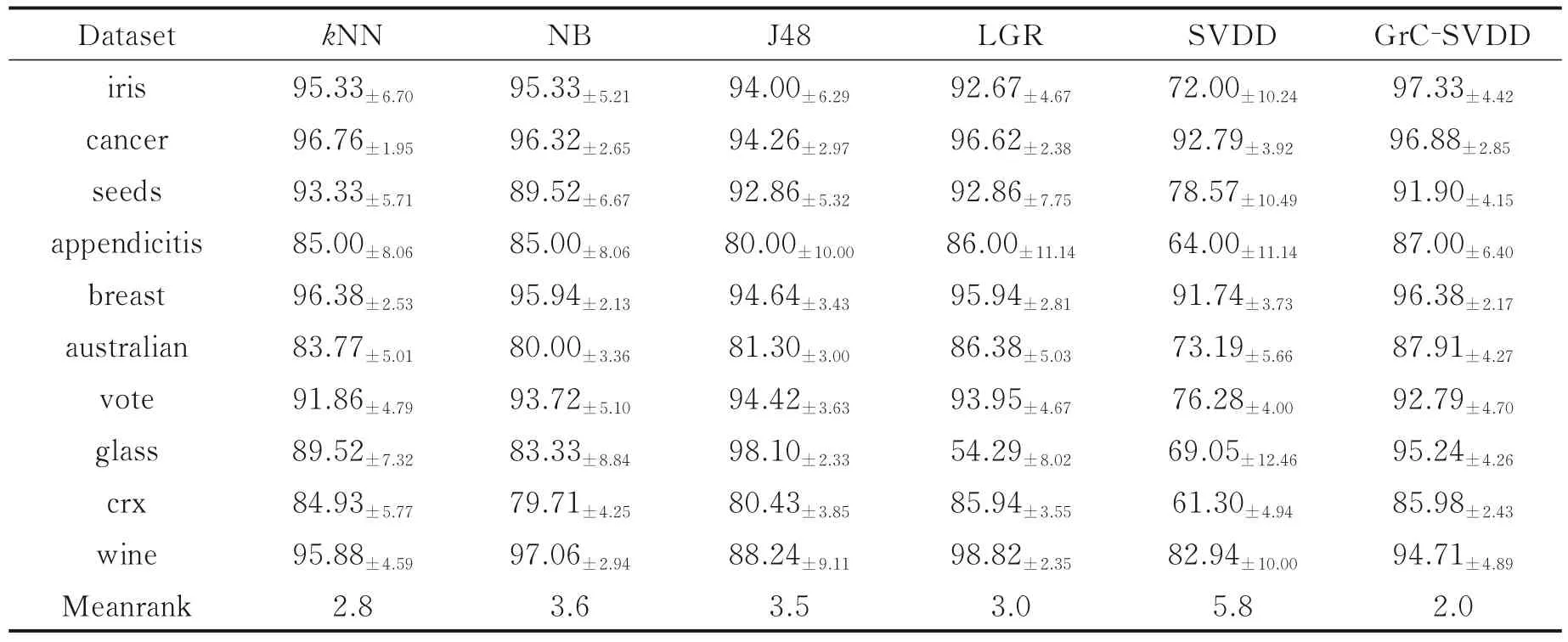
表3 算法精度对比Table 3 Accuracy comparison with other algorithms
4 结束语
针对SVDD 不能很好刻画数据边界的问题,提出了基于粒计算的支持向量数据描述分类方法,即GrC⁃SVDD,通过实验分析得到如下结论:(1)为了提高SVDD 在单一决策边界上的分类能力,本文通过构造了多粒度层次属性集合,将单粒度超球扩展为了多粒度超球,使原本在单一决策边界上不可区分的样本在多粒度超球决策边界上变得可分。(2)在粒化过程中,选择了有利于边界描述的属性集合,使得本文方法能在少量属性上做出快速决策。不仅分类效果较好,而且模型泛化能力较强。(3)实验部分讨论了邻域半径δ和纯度阈值ε对分类结果的影响,并给出了取值建议。下一步研究工作:(1)本文是以一定步长改变参数值,通过观察实验结果来确定最佳参数。若步长设置不合理以及取值区间过大或过小,则将需要较多时间来得到最佳结果。接下来的工作将研究更加高效的参数寻优方法,以进一步提高模型的分类性能。(2)本文方法默认模型输入是数值型数据,但在大数据中,数据具有维数高和特征形式多样化的特点。如何利用GrC⁃SVDD 对混合型数据进行复杂分类,这也将是下一步的研究重点。

