基于模糊神经网络的永磁同步电机伺服系统研究

王培宇，马立新

(上海理工大学 机械工程学院，上海 200093)

永磁同步电机(Permanent Magnet Synchronous Motor，PMSM)凭借其功率密度高、调速范围宽、效率高等优点，在工业上得到了广泛的应用[1-3]。PMSM的高性能控制方式主要包括矢量控制和直接转矩控制。其中，矢量控制系统一般采用转速、电流双闭环比例积分微分(Proportion Integration Differentiation，PID)控制结构[4]。在实际应用中，常规的PID控制作为线性控制，不仅难以满足系统的控制精度，且当负载发生扰动时动态性能较差[5-6]。

为取得更好的控制效果，许多学者对PMSM控制方法展开了研究。文献[7]利用模糊PID在线整定速度环的PID参数，减小了系统的超调量，但动态性能提升较小。文献[8]将模糊控制应用到转速环上，并利用粒子群优化算法调整比例因子和量化因子，提高了系统的响应速度，但启动时转矩波动较大。文献[9]设计了伸缩因子，动态调整模糊PID控制的论域，提高了模糊规则的作用效率。文献[10]将模糊控制分别应用到转速环和电流环上，提升了系统的动态性能，但两处模糊控制使实现较为复杂。

本文在PMSM矢量控制系统的基础上结合智能控制方法，设计了基于模糊径向基神经网络的PID控制策略，并将其应用到调速系统中。该方法以转速误差和误差变化率为输入，动态调节比例、微分、积分系数，提高系统的动、静态性能。最后，通过仿真与实验验证了设计的有效性。

1 PMSM矢量控制系统

PMSM的矢量控制实质上是通过坐标变换，使定子电流的励磁分量id和转矩分量iq实现解耦，从而对交流电机磁通和转矩进行控制[11-12]。本文采用id=0的控制方式，将三相电流通过Clark变换和Park变换转化为d-q轴上的电流，取q轴方向为定子电流的方向，则d轴电流为0，实现解耦[13]，达到近似于直流电机的控制性能。其结构如图1所示，主要由转速环、电流环、逆变器、空间矢量脉宽调制算法和PMSM组成。

图1 模糊RBF神经网络PID控制PMSM系统结构Figure 1. The structure of fuzzy RBF neural network PID control PMSM system

经过从三相坐标系向旋转坐标系的坐标变换后，d-q轴坐标系下的电压方程为

(1)

定子磁链方程为

(2)

转矩方程为

(3)

式中，ud、uq分别是旋转坐标系中d轴、q轴电压分量；id、iq分别是d轴、q轴电流分量，本文中取id=0；RS是定子电阻；ωr是转子电角速度；Ld、Lq分别是d轴、q轴电感；Ψf是转子磁链；pn是电机极对数。

2 模糊径向基神经网络PID控制器

2.1 控制器原理

模糊径向基神经网络结合了径向基(Radial Basis Function，RBF)神经网络和模糊控制的优点，既解决了模糊规则不能在线调整的问题，也降低了神经网络参数设置的随机性[14]。本文将模糊RBF神经网络与增量式PID控制相结合，实现PID参数的自动调整，其结构如图2所示。

图2 模糊RBF神经网络PID控制结构图Figure 2. The diagram of fuzzy RBF neural network and PID control structure

模糊RBF神经网络PID控制器包括模糊RBF神经网络系统和增量式PID控制器[15]。本文中，设计模糊RBF神经网络控制器以系统给定转速与实际转速间的差值e和误差变化率ec作为输入，经过模糊RBF神经网络的计算，得到整定后的PID参数，包括动态调整比例系数kp、积分系数ki和微分系数kd。

2.2 增量式PID

增量式PID是一种输出控制量增量的离散式PID控制方式，其输出为

Δu(k)=kp[e(k)-e(k-1)]+kie(k)+

kd[e(k)-2e(k-1)+e(k-2)]

(4)

式中，k是采样时刻；Δu(k)为增量式PID的控制增量，仅与前三次采样的误差值相关，不需要累加，可有效提高运算效率。由Δu(k)得控制量u(k)如式(5)所示。

u(k)=u(k-1)+Δu(k)

(5)

2.3 模糊RBF神经网络PID设计

模糊RBF神经网络由4层网络结构组成，如图3所示。为了满足PID控制器的控制要求，选取网络节点数为2-7-49-3的神经网络。网络以e和ec为输入，依次经过模糊化层和模糊推理层的计算，得到kp、ki、kd的值并作为PID控制器的参数。

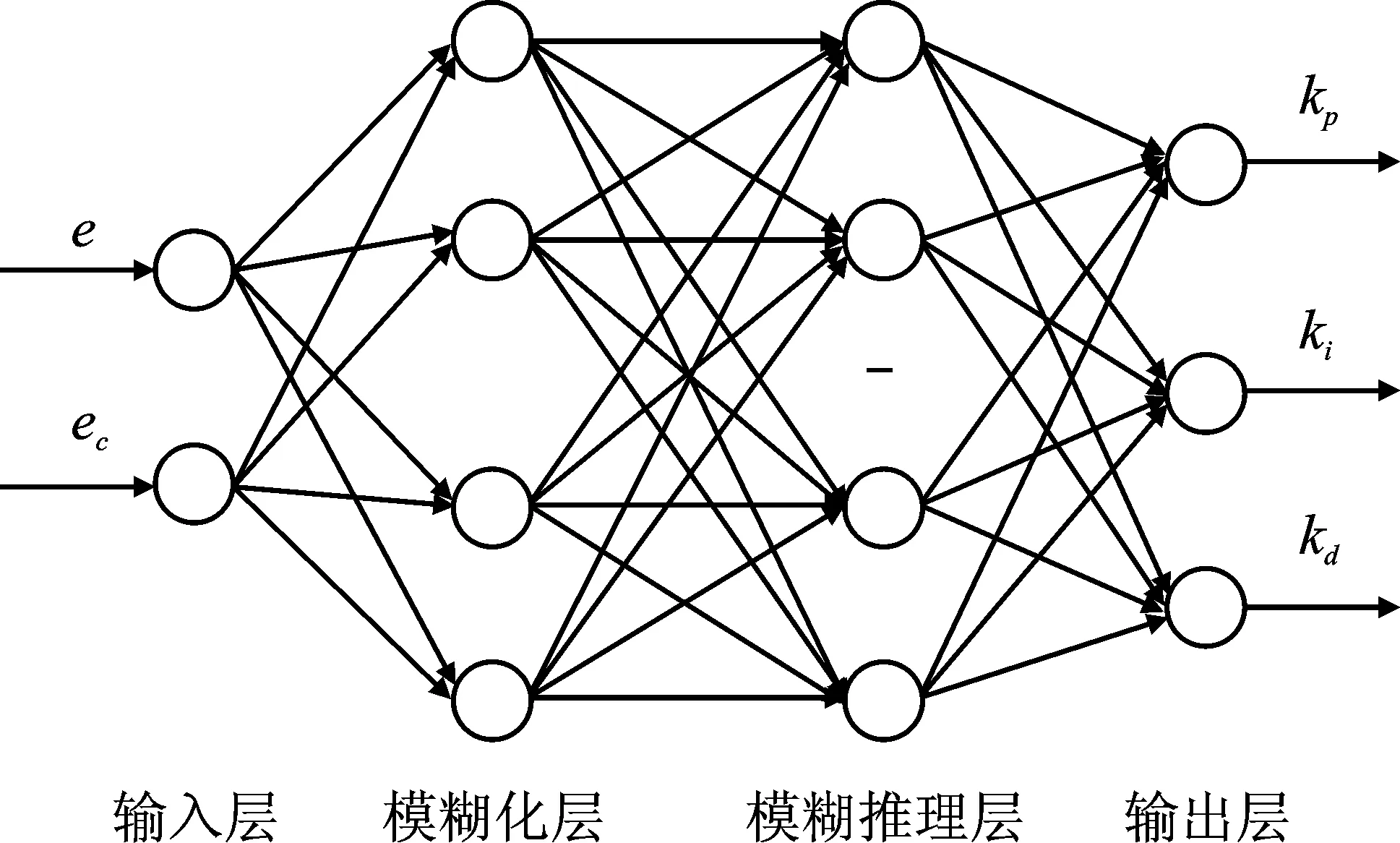
图3 模糊RBF神经网络结构Figure 3. Fuzzy RBF neural network structure

网络的输入层包括两个节点，分别接收e和ec并输出到下一层网络，每个节点的输入输出如式(6)所示。

f1(i)=xi

(6)

模糊化层包括7个节点，将输入的确定量模糊化，再根据径向基函数计算各自对应的隶属度[16]，该层输出为

(7)

式中，i表示输入变量；j表示模糊集合；bij、cij分别表示隶属函数的标准差和均值。

模糊推理层包括49个节点，代表49条模糊规则，作用是通过模糊化层各个节点之间的模糊运算实现模糊规则的对应[17]。每个节点的输出为

f3(j)=f2(1，j1)·f2(2，j2)

(8)

式中，j1、j2是模糊化层节点数；j是模糊推理层节点数。

输出层包括3个节点，作用是将模糊量清晰化，输出值即为kp、ki、kd的值

(9)

式中，l表示输出层节点数；W表示第3和第4层之间的连接权矩阵。

模糊RBF神经网络需要更新的参数包括连接权矩阵W、高斯函数宽度矩阵B和高斯函数中心矩阵C。采用增量学习规则进行调整，目标函数为

(10)

式中，r(k)、y(k)分别是控制器的输入与输出，在电机系统中分别代表电机的给定转速n*和实际转速n；r(k)-y(k)表示第k次迭代的误差e。为取得E的最小值，本文采用梯度下降法对参数进行调整[18]。首先，利用误差反向传播算法计算目标函数对各参数的偏导

(11)

(12)

(13)

然后根据梯度优化算法调整wij、bij、cij

α[wij(k-1)-wij(k-2)]

(14)

α[cij(k-1)-cij(k-2)]

(15)

α[bij(k-1)-bij(k-2)]

(16)

式中，η为学习率(η∈[0，1])；α为惯性系数(α∈[0，1])。

根据上述分析，模糊RBF神经网络PID控制的算法步骤如下：

步骤1设定神经网络各层节点数，初始化参数η、α、W(0)、B(0)、C(0)；

步骤2获取给定转速n*(k)和实际转速n(k)，将其分别作为控制器的输入r(k)与输出y(k)，得到转速误差e(k)和误差变化率ec(k)=e(k)-ec(k)；

步骤3计算网络各层的输入输出和PID控制器输出Δu(k)，在PMSM矢量控制系统中利用u(k)得到下一采样时刻的y(k)；

步骤4更新参数wij、bij、cij；

步骤5迭代次数k=k+1，返回步骤2进行下一时刻的计算。

3 系统仿真与分析

3.1 系统仿真

基于上述理论，本文在Simlink平台下建立PMSM矢量控制系统模型，采用id=0控制策略，在系统转速环上分别采用常规PID控制和模糊RBF神经网络PID控制进行对比。本文采用的PMSM各项参数为：定子电阻R=0.958 Ω，极对数pn=4，转动惯量J=0.003 kg·m2，磁链Ψf=0.182 7 Wb，定子电感Ld=5.25 mH，Lq=12 mH。采用S函数编写模糊神经网络算法，经过试验设定学习率η=1，惯性系数α=0.4。

3.2 结果与分析

为了验证模糊RBF神经网络PID控制方法下系统在高速和低速运行状态下的性能，分别对两种控制方式下的系统在相同条件下进行仿真对比，观察电机转速和转矩的响应情况。设定启动时负载转矩TL为10 N·m，在0.3 s和0.6 s时分别变化为15 N·m和5 N·m，系统分别在给定转速n*为1 000 rpm和200 rpm的条件下运行，仿真结果如图4～图9所示。

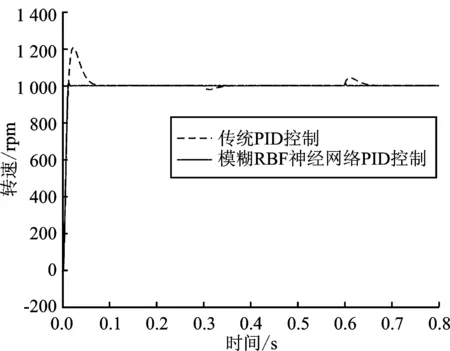
图4 1 000 rpm时速度响应曲线Figure 4. Rotate speed curve at 1 000 rpm

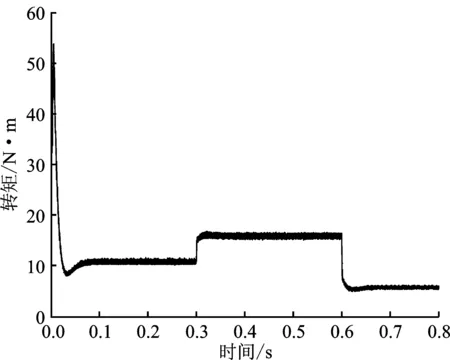
图5 1 000 rpm时传统PID控制转矩曲线Figure 5. Torque curve of traditional PID control at 1 000 rpm

图6 1 000 rpm时模糊RBF神经网络PID控制转矩曲线Figure 6. Torque curve of fuzzy RBF neural network PID control at 1 000 rpm

从图4～图6可看出，在高速运行时，模糊RBF神经网络PID控制系统转速能够快速稳定，超调量和启动时间都小于传统PID控制系统，且转速在负载发生扰动时所受影响较小， 抗干扰能力强。在传统PID控制下，启动约0.07 s后电磁转矩稳定在给定转矩附近，转矩脉动较大。而模糊RBF神经网络PID控制时，电磁转矩在启动0.02 s后便快速达到稳定，在两次负载变化后，电磁转矩虽略有波动，但恢复到稳定所需时间更短，稳定后对转矩脉动的抑制效果更好，具有更好的鲁棒性。

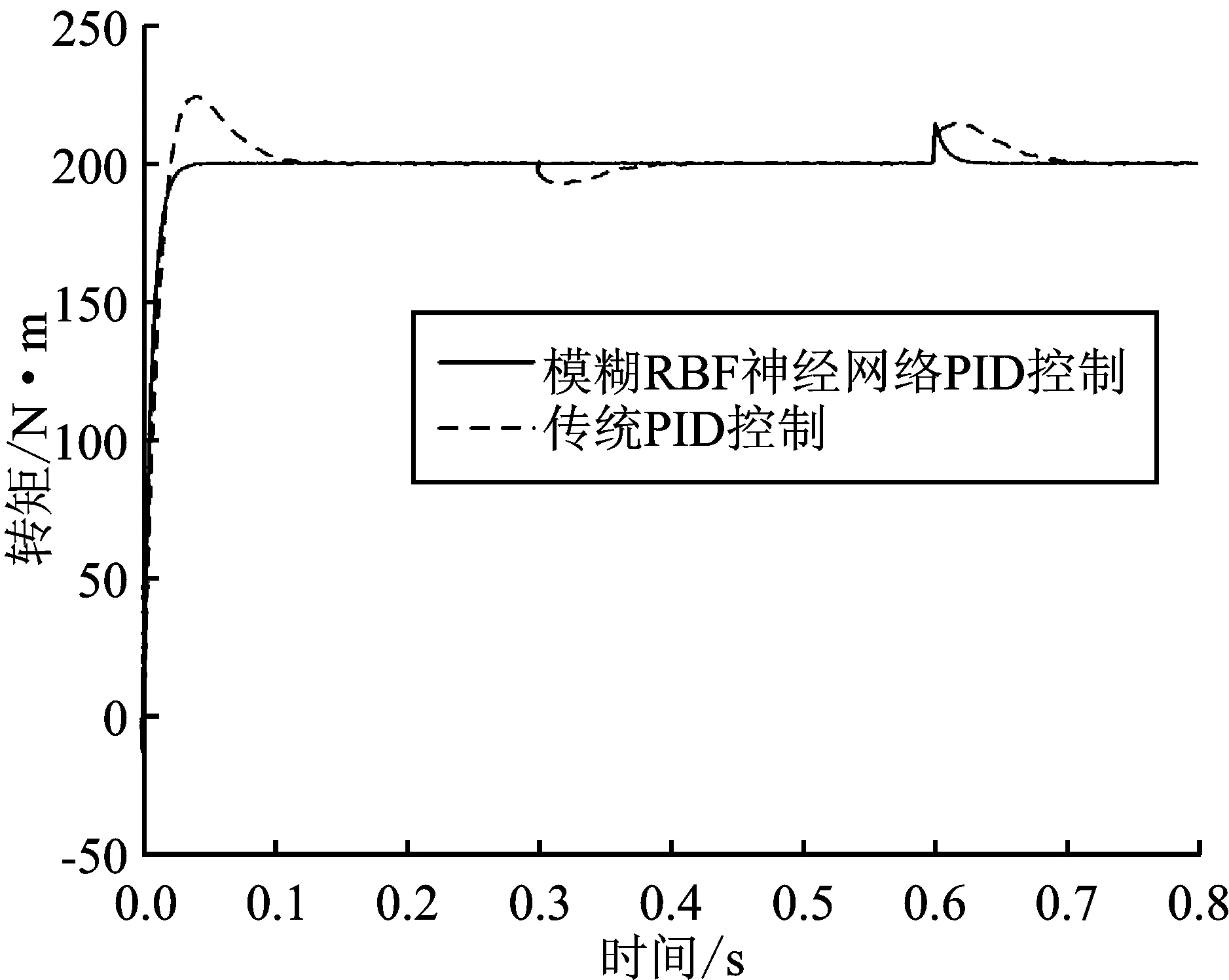
图7 200 rpm时速度响应曲线Figure 7. Rotate speed curve of 200 rpm

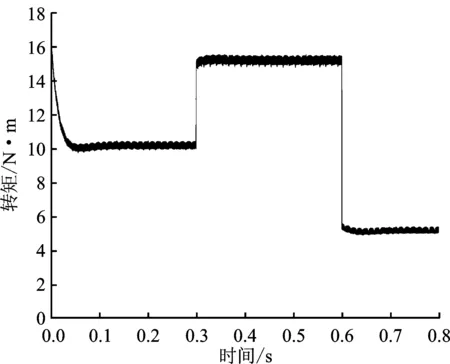
图8 200 rpm时传统PID控制转矩曲线Figure 8. Torque curve of traditional PID control at 200 rpm

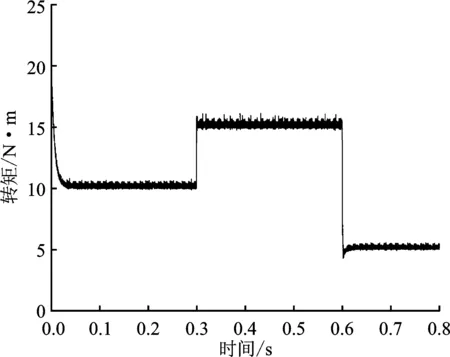
图9 200 rpm时模糊RBF神经网络PID控制转矩曲线Figure 9. Torque curve of fuzzy RBF neural network PID control at 200 rpm

图7～图9对应低速状态下的转速、转矩曲线。低速运行时，模糊RBF神经网络PID控制系统转速几乎无超调，在达到200 rpm后便稳定运行，转速在负载发生扰动时出现波动，但波动幅度小，恢复稳定比传统PID控制系统更快，动态响应更好。模糊RBF神经网络PID控制系统的转矩响应较快，可以迅速稳定在设定值，且转矩脉动幅度较小。仿真结果数据对比如表1所示。

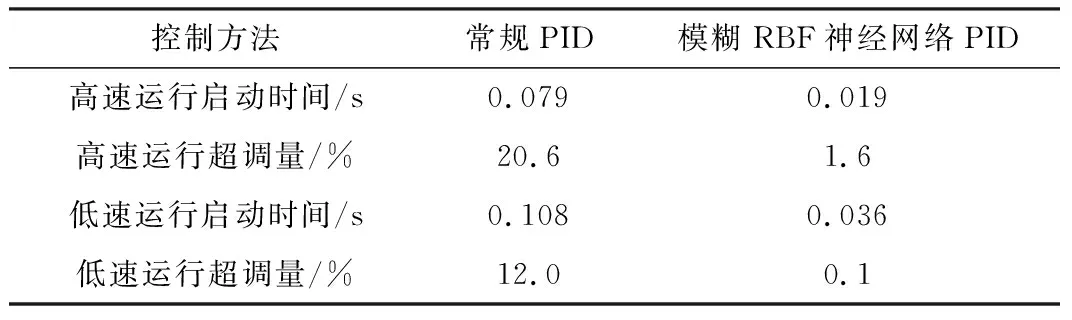
表1 仿真结果数据对比

4 实验结果

本文基于32位浮点数字信号处理器(Digital Signal Processor，DSP)TMS320F28335的电机控制平台进行搭建。利用1250线编码器监测电机转子实时位置，经过计算得到电机转速并将其保存到CCS软件中。电机空载启动，转速设为1 000 rpm。

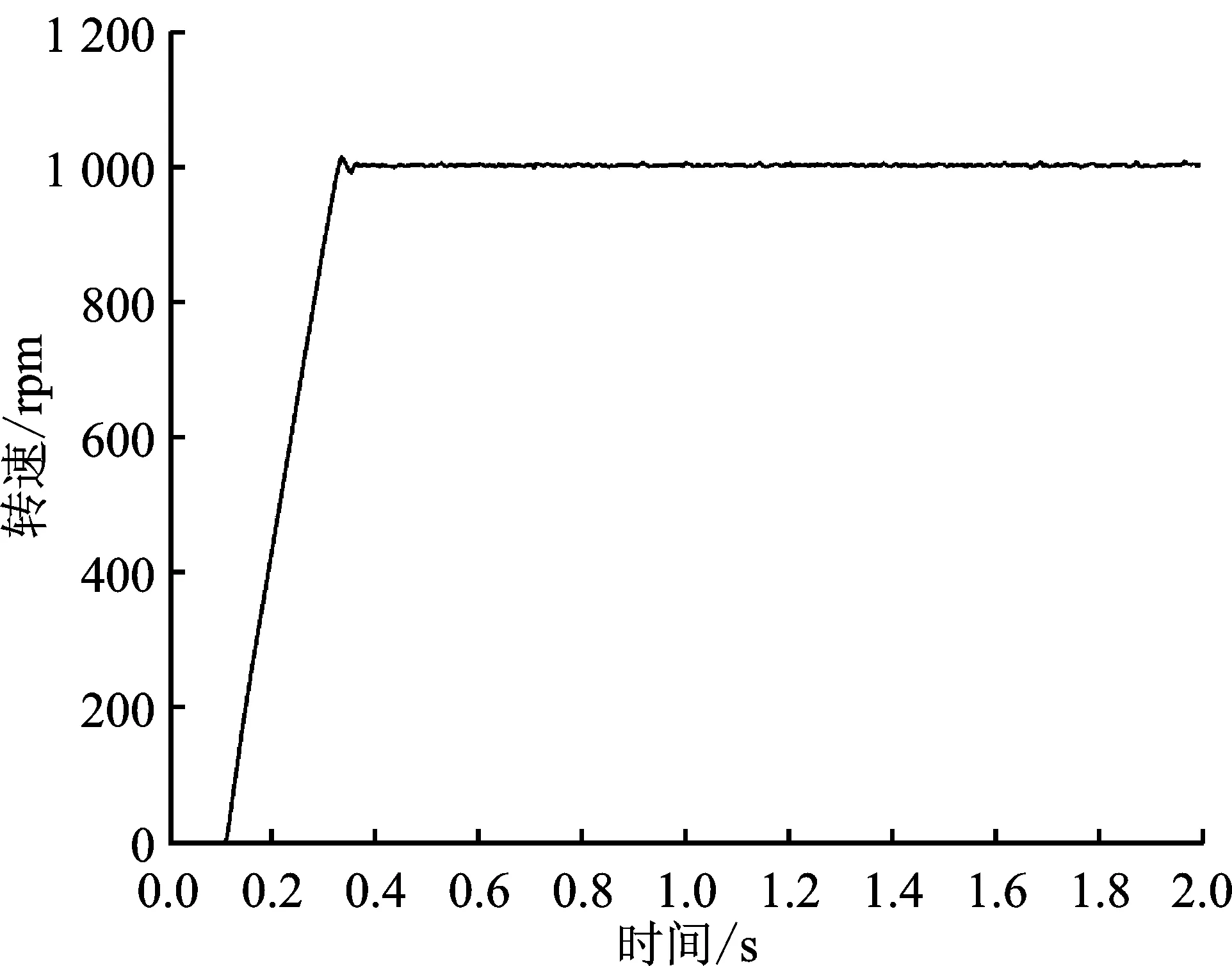
图10 1 000 pm时转速波形Figure 10. Speed curve at 1 000 rpm

图11 1 000 rpm时A相电流波形Figure 11. A-phase current curve at 1 000 rpm

图10和图11分别为电机启动至稳定的转速曲线和稳定运行时的A相电流曲线。可以看出，转速超调较小，恢复稳定快，具有较好的动态响应速度。转速达到给定值后，波动较小，误差在±5 rpm范围内，且相电流保持正弦波变化，可以平稳运行。

5 结束语

本文对PMSM的矢量控制策略进行了分析。PMSM是非线性系统，传统的PID控制不能进行实时调整，难以满足工业应用的高精度控制要求。因此，针对传统控制方法下系统存在的动态响应慢、超调量大、抗干扰能力差等问题，本文提出了模糊RBF神经网络PID控制策略，可不依赖于电机系统的精确模型进行控制。该策略结合神经网络和模糊控制的思想，并采用增量式PID的控制模型，以误差和误差变化率为输入，可以动态整定比例、微分、积分系数。

将该方法应用到PMSM转速环中，并与传统控制方式进行对比。仿真结果说明，模糊RBF神经网络PID控制的电机系统响应更快，超调量小，因负载扰动导致的转速发生大幅度波动的现象有所改善，电磁转矩也能够快速达到给定值并稳定，系统具有动态响应快、鲁棒性好的优点。本文利用DSP搭建实验平台进行了实验，证明了该方法的可行性，为伺服电机的实际应用提供了参考。