电场耦合式无线电能传输频率分裂特性分析
杨 锐,孙岩洲,余江华,张蒙飞,韦延方
(1.河南理工大学 电气工程与自动化学院,河南 焦作 454000;2.国网安徽省电力有限公司 芜湖县供电公司,安徽 芜湖 241000)
随着科学技术的飞速发展与生活水平的不断提高,电气设备的供电方式在潜移默化中发生着变化,供电方式也逐渐趋于智能化、安全化,因此无线电能传输技术(Wireless Power Transfer,WPT)应运而生[1-4]。传统的输电方式易发生用电安全方面的事故,严重时还会危及到生命财产安全[5-6]。WPT的产生使电气设备摆脱了传统的充电方式,能够灵活地应对各种复杂的充电环境,具有安全、便捷的特点和良好的应用前景[7-10]。
但是,WPT系统存在严重的频率分裂(简称频分)现象[11-13]。文献[14]利用控制理论中的Bode图对串联对称型WPT系统中的传递函数进行考察分析,得出频分现象的存在是因为系统中存在两个二阶的振荡环节所引起的。文献[15]通过系统中是否外接串联电容来进行对比分析。系统在外接电容进行调谐时会在某个临界值处发生频分现象,原因是系统存在不同的谐振频率,而不进行外接电容的系统则未发生频分的现象。文献[16]以四线圈为基础,建立并分析了系统完整简化的数学模型,通过进一步的推导得到了系统效率的表达式,再根据功率流理论揭示了源内阻、发送侧与接收侧的互感均为发生频分现象的相关因素,并提出了消除频分的措施。文献[17]通过对WPT串串模型的分析建立了其互感模型,得到关于电压增益的解析式,通过仿真详细分析了系统在3种不同状态下的频分现象,并对其有效传输距离进行了有效定义。目前对于磁场耦合式无线电能传输(Inductive Coupled Power Transfer,ICPT)系统的频分研究较多,但对电场耦合式无线电能传输(Electrical-field Coupled Wireless Power Transfer,ECPT)系统频分的研究较少[18-20]。
本文在已有的研究基础上[21],以恒流输出的双侧LCLC补偿拓扑结构的ECPT系统作为研究对象,首先通过理论方式建立系统等效电路,推导出系统效率与重要参数之间的关系式来分析其频分现象;然后通过MATLAB仿真软件详细分析系统效率关于重要参数的影响规律;最后通过实验平台得到的实验数据验证了仿真结果的正确性,并得出ECPT系统频分的出现条件以及能够获得最大效率的条件。
1 双侧LCLC补偿ECPT系统分析
1.1 双侧LCLC补偿ECPT系统原理分析
双侧LCLC补偿网络的ECPT系统拓扑如图1所示,耦合机构由耦合电容Cs1、Cs2构成。系统采用高频高效的E类功率放大器作为电源,采用铜质薄板构成耦合机构。其中,L1、C1、L2、C2、Lf1、Cf1、Lf2、Cf2是补偿元件,构成系统的双侧LCLC补偿网络,I1、I2分别为系统的输入、输出电流,RL是等效负载元件,Zin为整个系统的输入阻抗。由于耦合电容一般均在皮法的范围内,所以需要在其两侧并联电容来减小系统所需的补偿电感的体积。系统采用完全相同的耦合极板,则Cs1=Cs2,表达式为
(1)
式中,S是耦合极板的有效面积;d是极板耦合传输间距;ε是耦合极板间的介电常数。
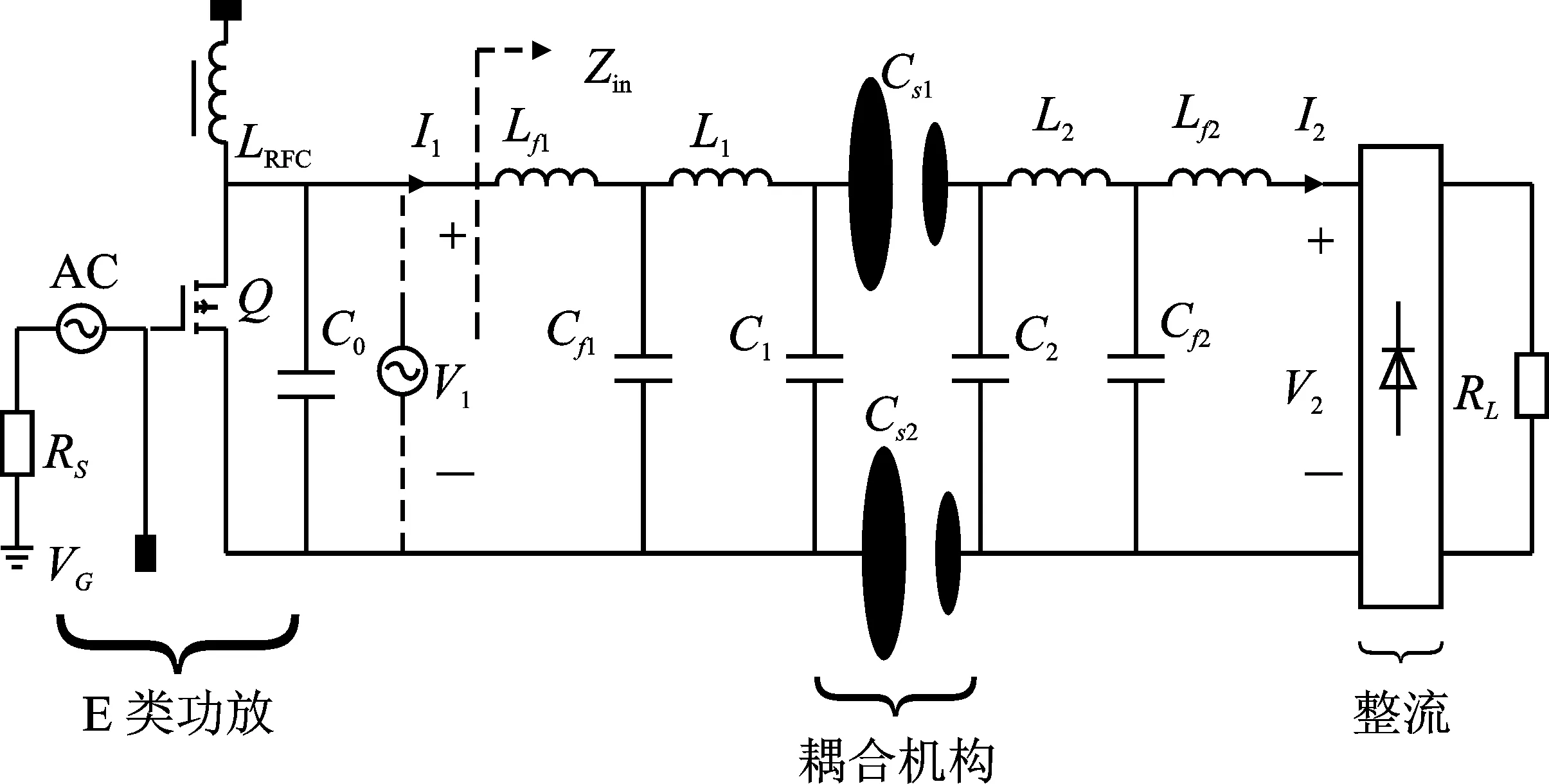
图1 LCLC补偿ECPT系统电路图Figure 1. Circuit diagram of LCLC compensation ECPT system
为了方便分析电路网络中的恒流特性,将图1中的E类功率放大器[22]等效为系统的输入电压V1,输出侧电压等效为V2,极板等效总电容为Cs。又由于Cs1=Cs2,则Cs的表达式为
(2)
ECPT系统采用的是双侧LCLC补偿网络,系统拓扑呈现的是对称式结构,所以对称位置上的所有元器件参数均是相等的,因此有Lf1=Lf2,L1=L2,Cf1=Cf2,C1=C2。极板耦合电容器与并联电容器可等效为一个总的电容器Ck,其表达式为式(3)。
(3)
1.2 双侧LCLC补偿ECPT系统恒流特性分析
根据LCLC补偿的拓扑电路,在系统的设定频率fN下,Lf1与Cf1会产生谐振,而Cf1与L1中的一部分电感会产生谐振,L1的另一部分电感与总的电容器Ck产生谐振,则参数满足式(4)。
(4)
图2是仅在输入电压源V1激励下的系统电路图,当耦合机构的介质损耗角较大时,所衍生出的电阻不可被忽略。图中的RCs是耦合电容的串联等效电阻,图中的虚线表示此路不通(即该通道可视为开路状态)。
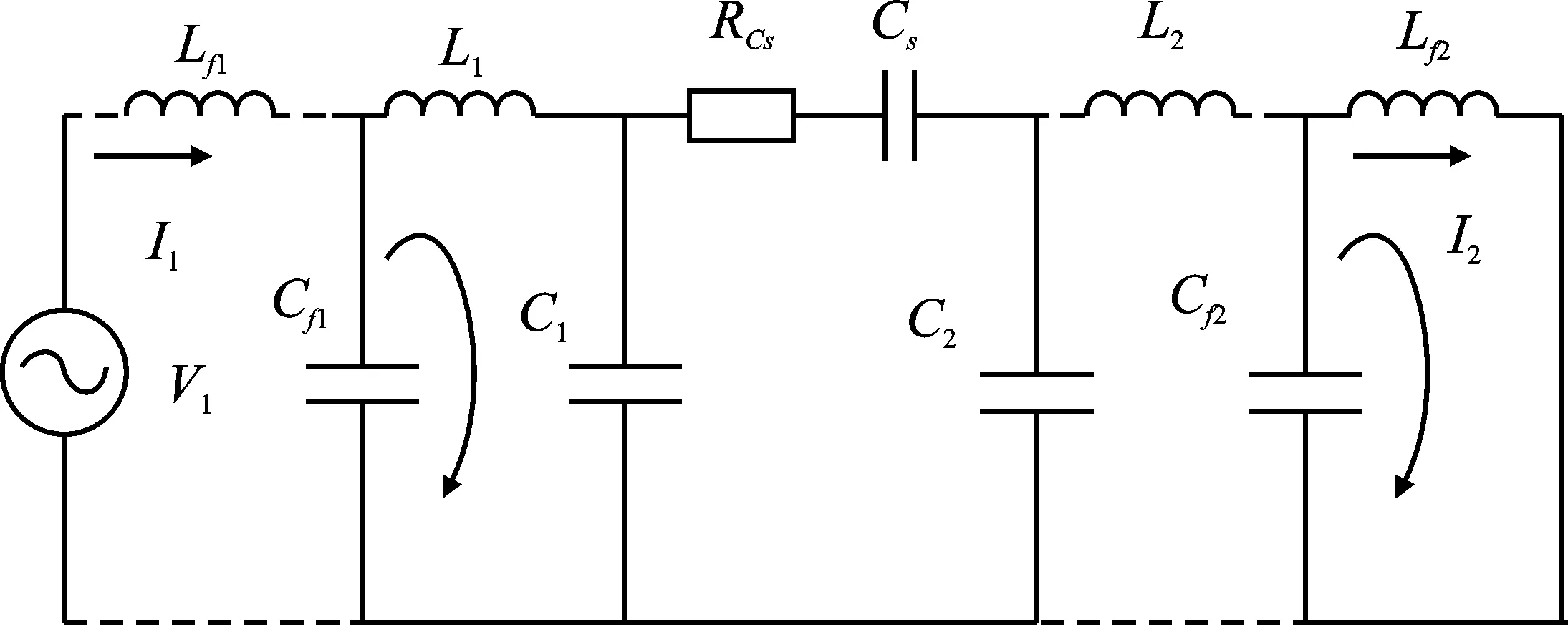
图2 输入电压激励下的系统电路Figure 2. System circuit excited by input voltage
依据基尔霍夫电压定律可得
(5)
由上述表达式可知,I2与易变参数Cs以及频率f有关,但与负载无关,因此在元器件处于参数设定值时,无论负载如何变化,都不会影响到I2。故可将输出电流I2视为恒定电流,则该系统具有恒流输出特性。
1.3 双侧LCLC补偿ECPT系统电路分析
ECPT系统工作在设定频率时处于串联谐振状态,本文所设定的系统固定频率为13.56 MHz,传输功率为30 W,系统输入侧与输出侧的电压幅值均设定为55 V,负载为50 Ω,由耦合极板构成的耦合电容值为200 pF,为降低系统补偿电感的体积所设定的并联电容值为500 pF。根据图1中的ECPT系统图,利用电路理论方面的知识可知电压增益|Gv|=|V2/V1|,η=Pout/Pin,推导可得
(6)
式中,Zin是系统的输入阻抗。从系统图及输出功率可以看出,输出功率受易变参数、等效阻抗与负载的影响,从而使系统损失一部分的功率,则系统效率就会随之变化。
联立以上各式可得系统效率η的表达式
(7)
由上式可知,系统中存在的易变参数有系统频率、耦合电容,但系统的效率η不仅与易变参数有关,还与负载有关。
2 系统仿真与分析
根据式(7),系统效率可认为是η=k(f,Cs),也就是关于频率f与耦合机构电容Cs的函数。根据系统设定参数以及函数关系式,运用MATLAB仿真软件对双侧LCLC补偿网络的ECPT系统的频分现象进行详细分析,根据式(4)与式(6)进行计算,系统设定参数如表1所示。

表1 系统元件参数
系统效率随f和Cs的变化趋势如图3所示。根据图3可以看出,图中出现了多个制高点,此处的系统性能输出是比较好的,同时也能看出系统在参数设定值附近的效率是比较高的,但也出现了明显的频分现象。因此,根据图3可得出以下结论:
(1)从系统频率f轴的视角看,当远离设定的系统频率fN时,系统的效率较低,基本处于不工作的状态。在逐渐接近设定频率fN时,系统的效率则会随之不断提高,系统处于比较好的工作状态。在设定频率fN处,系统的效率并未达到最高,而是在设定频率fN的两侧达到最大值,出现明显的频分现象,fN左侧的称为奇模分频,fN右侧的称为偶模分频;
(2)从耦合机构机构电容Cs轴的视角来看,系统效率出现两个明显的峰值,且系统效率是随着耦合机构电容Cs的增大而逐渐增大。但当耦合电容值Cs较小时,系统效率较低,甚至无法传输电能;
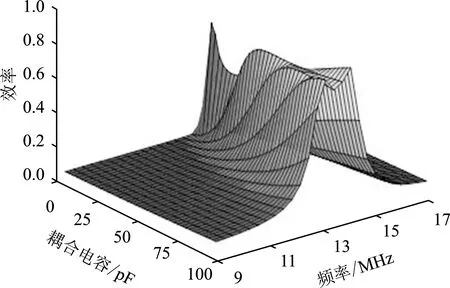
图3 η随Cs和f变化的三维图Figure 3.Three dimensional graph of η with the change of f and Cs
(3)综合f、Cs来看,在奇模分频的左侧,随着系统频率f以及耦合机构电容的增大,系统效率η也在逐步增大;在偶模分频的右侧,随着系统频率f以及耦合机构电容的增大,系统效率η将会逐步减小。当系统频率偏离设定频率fN时,系统效率η均呈现快速下降的趋势。当所提供的频率f太高或太低时,无论耦合电容Cs的相对位置如何变化,系统的效率η均较低。
2.1 效率随耦合电容的变化分析
图4是图3关于频率变化的剖析图。
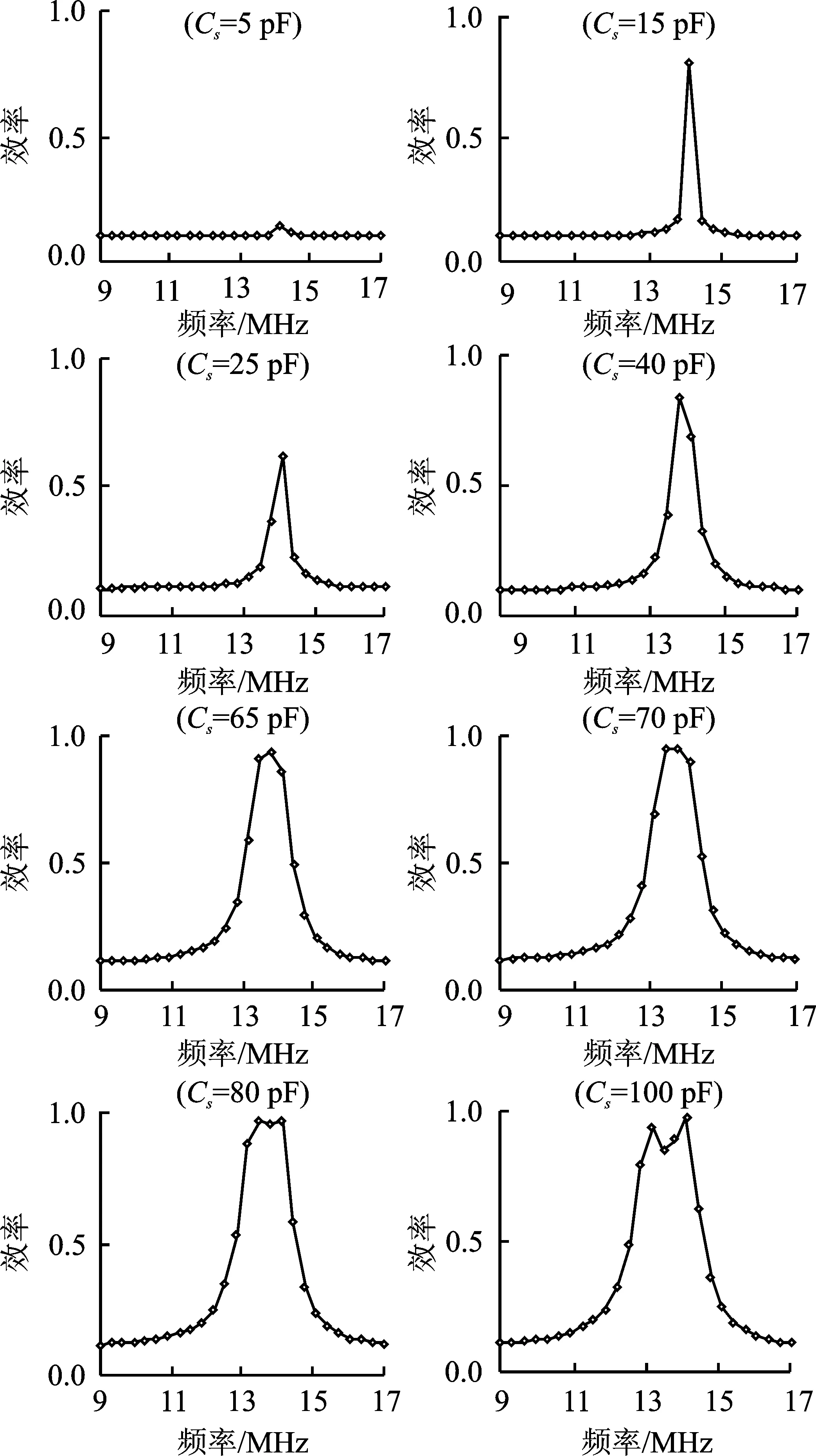
图4 不同耦合电容值下效率随频率的变化Figure 4.Variation of η with f under different coupling capacitance values
从图4可知,在耦合电容值特别小时,系统的传输效率η极低,但当耦合机构的电容值Cs﹤80 pF时,随着系统频率的逐步增大,系统的效率η呈现出先增大后减小的趋势,且系统没有频分现象。当耦合机构的电容值Cs>80 pF时,系统效率η随频率f变化的趋势无显著变化,但最大的不同为系统效率η出现了双峰值,即频分现象。当耦合机构的电容值Cs=80 pF时,系统开始出现频分现象,该点称之为频分点(Csplit)。当耦合机构的电容值Cs≤65 pF时,系统的变化趋势基本符合前面所分析的情况,但不同之处在于系统效率η在f=14 MHz处取得最大效率,该点称之为效率关键点(fcrucial),同时也说明该ECPT系统存在些许的频率偏移现象。当耦合机构的电容值Cs>65 pF时,该ECPT系统的频率偏移现象消失,但频分现象逐渐地在系统中出现。当耦合机构的电容值Cs=70 pF时,系统的频率偏移现象消失,该点称之为频率回归点(Creturn)。因此系统要确保耦合机构相对位置固定,在避免其产生交叉耦合的同时,也能使系统传输性能更好。
2.2 效率随频率的变化分析
图5是图3关于耦合机构电容值变化的剖析图,由于Cs较难达到100 pF,所以设定最大值为95 pF。

图5 不同频率下效率随耦合电容的变化Figure 5. Variation of η with Cs under different f values
从图5可看出,在系统频率f≤13 MHz时,伴随着电容值不断增大,效率η将会逐步增大。当系统频率f=13 MHz时,效率η可达90%。同时可以看出,只有频率f在13.56 MHz左右且Cs>60 pF时,系统效率η基本维持在90%以上,因此系统在f=13.56 MHz时的传输性能最为稳定。当频率高于14.5 MHz时,其最大效率将会逐步减小,说明系统传输电能的能力在逐步减弱。因此系统所提供的频率在fN附近时,系统效率η均可达到90%,系统的传输性能也比较稳定。
综合可知,当系统频率f与耦合机构的电容值Cs接近其设定值时,系统的传输效率η可达到90%,但系统出现的频分现象也较为严重,只有当该ECPT系统工作在频分点(Cs=80 pF)且信号发生器提供的频率为设定值fN(13.56 MHz)时,系统能够在获得较好传输性能的同时避免频分现象的发生。
3 实验验证
3.1 实验设置
为了验证关于ECPT系统的理论推导与系统仿真的正确性,根据图1中的双侧LCLC补偿网络的系统图以及所计算出的元件值搭建出如图6所示的系统实验装置平台。实验所需要的高频电源是由E类功放提供的,由于E类功放的工作频率大小为13.56 MHz,因此本文选用漆包线来绕制空心电感,其半径为0.5 mm。耦合机构所采用的是自制的等效耦合电容值为200 pF的耦合模型,并采用集成度高的MAX038作为实验的信号发生器,通过示波器来测量系统的输出。

图6 系统实验图Figure 6. System experiment diagram
3.2 效率结果分析
图7是当耦合机构Cs的电容值分别为5 pF、50 pF、70 pF、80 pF、90 pF时,ECPT系统效率η随频率f的变化规律。从图中可以看出,随着耦合机构电容值Cs的增大,系统效率也随之增大。当耦合机构的电容值Cs过低时,系统效率随频率f的变化趋势特别小,同时还存在频率偏移现象。当耦合机构的电容值在频率回归点(Cs=70 pF)时,系统的频率偏移现象消失,但系统的传输能力还未达到75%。当耦合机构的电容值在频分点(Cs=80 pF)时,系统开始出现频分现象,但系统效率有所提升,最大值能够达到85%。当耦合机构的电容值大于频分值时,系统效率η虽有提升,但总的来说提升不够显著,而频分现象逐渐显著。可以看出,由于实验测量仪器的精度、测量误差以及电感的集肤效应等因素,实验部分的效率比仿真部分的效率小,但这与章节2仿真部分的数值分析结论是一致的。

图7 实际耦合电容值下效率随频率的变化Figure 7. Variation of η with f under actual coupling capacitance values
电路使用50 Ω的标准假负载来模拟系统所带负载。为了获得较好的系统效率,使系统的耦合机构Cs保持最大耦合电容值,并适当调大频率f到效率关键点(fcrucial)。在这种参数设定下的实验波形如图8所示,测得输出电压的幅值大小为50.6 V,输出电流的幅值大小为1.06 A,则系统的最佳效率可达到89.4%。
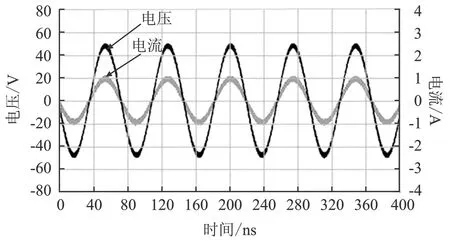
图8 实验波形图Figure 8. Experimental waveform
4 结束语
本文以双侧LCLC补偿拓扑结构的ECPT系统作为研究对象,通过理论推导、仿真数值分析以及实验证实了频分现象的存在。结果显示,在双侧LCLC补偿拓扑结构的ECPT系统中,输出电流对于负载来说具有恒流源的输出特性。当耦合机构的电容值在频分点(Csplit)以下时,系统不会出现频分现象,虽然此时可以避免系统出现频分现象,但系统将会出现频率偏移。为了获得更大的效率,需把频率调至效率关键点(fcrucial)。在系统的耦合机构保持最大耦合电容值的同时,将频率f调至效率关键点,系统不仅可以获得最大的效率,还能获得较高的输出功率,从而使系统的传能性能达到最优。

