电子方舱热仿真的等效模型与参数优化

袁伟琪，叶 锐

（中国电子科技集团公司第三十八研究所，安徽 合肥 230088）

0 引言

作为战场上重要的作战节点，电子方舱经常暴露于严苛的环境之下，方舱需要耐受夏季55℃的高温和太阳辐照；冬季里-40℃的低温，这些环境因素使得方舱的保温性能要求很高，电子方舱的热性能设计对其正常工作至关重要。

方舱设计过程中需要同时考虑传热系数、电磁兼容性和结构强度等多种性能，其设计工作复杂。随着计算机技术发展，热仿真技术在电子方舱的环控设计中扮演了越来越重要的作用：黄健借助CFD软件模拟了车载医疗方舱风道，验证了数值方法的可靠性[1]；张梦龙等运用FLUENT软件分析空调不同送风参数对于方舱降温效果的影响，并提出了制冷系统冷气通路的改进措施[2]；陈文博等利用有限元辅助设计方法提升方舱升温过程设计的效率和精度，实验结果表明仿真计算结果误差在6%~22%，处于工程仿真误差范围之内[3]。

前人工作表明仿真分析方法辅助方舱设计的可行性和高效性。但方舱仿真中存在尺寸跨度大的问题，这会加大方舱的网格量，在稳态计算时尚可接受，一旦需要对方舱进行瞬时计算，模拟升降温过程，计算量将会非常大，耗时长，降低设计效率。针对方舱热仿真特点，使用了分步计算的方法对方舱进行模拟：先通过详细建模计算出方舱舱壁的等效导热率，再将方舱整体建模，利用前述等效参数减少整体仿真的计算量，达到提升计算效率的目的。同时针对方舱进行详细建模，对比了不同尺度下两种计算方式的计算量及仿真结果。

1 模型介绍

1.1 方舱模型

军用方舱是目前电子通信系统的主要载体之一，一般运用保温舱壁、空调及加热器等措施控制舱内环境参数。其中，方舱舱壁的保温性能决定了舱体的冷热负荷，对方舱环境参数和耗电量有显著影响。方舱传热系数是衡量舱壁保温性能的重要指标，针对方舱传热系数开展了一系列仿真工作，典型的方舱舱壁采用聚氨酯发泡中间加金属骨架的大板式形式，如图1所示，由隔热层、方舱骨架、内外蒙皮以及断热桥组成。

1.2 仿真模型

1.2.1 一般模型

一般热仿真中针对整个方舱（去除不影响传热的特征）进行建模，将所有特征一一建立模型并赋值，如图2所示。

图1 方舱舱壁模型

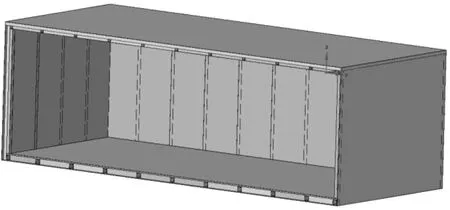
图2 电子方舱一般模型

根据国标要求，仿真计算时在方舱内部放置热源，通过调整热源散热量使内部空气温度稳定为20℃，外部气流速度不大于2 m/s，环境温度-35℃[5]，通过式（1）计算方舱传热系数。

式中，h为方舱传热系数，单位W/（m2K）；△T为舱内外温差，℃；A为方舱表面积，m2。

舱壁上特征较多，小尺寸的特征如骨架、蒙皮等长宽尺寸较大，而厚度小，且放置方向不同，仿真软件划分网格时会以薄壁厚度为最小尺度为基准，这会带来大量非必要的网格，使得模型网格量大幅度增加，提高计算量。

1.2.2 等效模型

为了减少仿真计算量，根据几何模型简化原则，在方舱仿真时分成两步进行：将舱壁作为一个整体看待，先计算出单位长度的模块舱壁的热物性；建立简化方舱模型，利用上一步求得的热物性为舱体赋值，从而减少计算量。详细过程如下：

第一步，舱体热物性计算：与一般模型类似，针对单位长度（主要取决于骨架间距）的舱体详细建模，利用仿真软件计算不同方向传热系数，进而计算出各个方向的热导率（式2），模型如图3所示。

图3 等效模型步骤1示意图

式中Q为通过舱壁的总热量，W；d为舱壁厚度，m；A为舱壁面积，m2。

第二步，建立方舱模型，其中舱壁为实心块状模型，如图4所示，并将等效参数赋值给舱壁。

图4 等效模型步骤2示意图

相比于一般模型，等效模型只有在第一步中针对单位长度的舱壁完整结构建立模型，减少了建模工作量同时可以大幅度较少仿真网格量，又不影响仿真准确度。

2 仿真结果

本节中利用第二节的方舱模型，利用软件分别进行仿真。

2.1 验证等效模型准确性

参考真实的方舱结构建立模型，验证等效模型的准确性。常见方舱的传热系数约为1.5 W/m2·K，典型舱壁材料见表1。

表1 方舱材料参数

参照GJB 2093A-2012 7.6节保温性试验方法，仿真分析时将外蒙皮壁面温度设置为-35℃，内蒙皮壁面温度设置为20℃，通过计算漏热量，评估其散热性能。结果见表2、图5。

表2 等效模型第一步结果

图5 纵切面温度分布图

针对方舱及内部热源建模，多次迭代使内部温度为20℃（环境-35℃，风速最大约1.6 m/s），此时热源制冷量约为5000 W，利用公式（1）计算得方舱传热系数为1.46 W/（m2·K），结果见表3、图6。

表3 等效模型第二步结果

图6 横切面温度云图

结果表明，仿真结果与实测结果差距不超过3%，仿真结果准确可靠。

2.2 不同模型仿真结果对比

以壁厚150 mm，骨架50 mm*50 mm，骨架间距600 mm的方舱为例，对比两种仿真模型的结果，如下所示：

（1）等效模型

第一步：计算舱体导热率，结果见表4和图7。

表4 等效模型第一步结果

图7 纵切面温度云图

第二步，计算方舱传热系数，结果见表5和图8。

表5 等效模型第二步结果

图8 横切面温度云图

（2）一般模型

针对方舱整体建模，为了兼顾仿真精确度及效率，设置每个边上有两个节点，模型仿真，结果见表6和图9。

表6 一般模型结果

对比2种模型结果可其传热系数相差约6%，仿真结果较为接近；一般模型的网格数比等效模型高了一个数量级，等效模型可以有效减小仿真计算量，加快仿真速度和设计过程。

在仿真中发现，参数调整时不需要对第二步中的整体模型做过多修改。特别是调整骨架间距，在一般模型中需要改变每根骨架，而等效模型只需要调整模型第一步中的保温层长度，工作量精简许多。

图9 横切面温度云图

2.3 模型应用与实验验证

采用等效模型进行仿真，结合工程需要，方舱设计参数见表7。

表7 方舱结构设计参数

经等效模型计算，方舱传热系数仿真约为0.41 W/（m2·K）。以该参数设计某冷藏方舱，通过实验测得方舱传热系数约为0.38 W/（m2·K），等效模型仿真结果偏离约8%。

3 结语

军用电子方舱由于其提供良好的电子器件及人员工作环境而广被使用，在其设计过程中，热仿真是保证性能的重要环节。在保证仿真精度的前提下，提出了一种网格和计算量更小的模型，并对其进行验证。结果表明该模型有着较高的准确性，且相比于完整建模的一般模型，网格数大大减少，且在参数修改时更加方便，可以极大提高设计效率。