铝电解分子比预测算法研究及应用

赵子凌,李晋宏

(北方工业大学 信息学院,北京100144)

在铝电解生产过程中,铝电解的酸度是一项很重要的技术指标,因此如何测定和控制酸度是铝电解过程中的重要环节之一[1]。然而现代铝电解工艺普遍采用酸性电解质,此种电解质中含有游离的氟化铝以及各种添加剂[2](如氟化镁,氟化钙,氟化锂等);这些物质的存在导致电解质物相比复杂,且相互存在非线性关系,相互影响,使得分子比难以直接测量。另外,分子比是代表铝电解质成分的一个重要技术参数,对电解系统吨铝直流电耗和电流效率影响较大。故调整合理的电解质成分尤其是控制好分子比,对铝电解工业节能减排、提质增效是非常重要的[3]。

现代铝电解工艺中,普遍采用的是冰晶石-氧化铝熔岩电解法,该方法的基本原理:在铝电解槽中使用氧化铝作为主要材料,以冰晶石和氟化盐为熔剂,构成冰晶石-氧化铝均匀熔融体,将直流电通入电解槽,阴极上产生液态铝,阳极上产生的二氧化碳和一氧化碳等气态物质,与此同时在铝电解的整个过程中要保持能量与物料的动态平衡。液态电解质成分是保证电解过程能够正常进行的关键因素,而冰晶石就是液态电解质的主要成分。从分子结构上讲,它是由 3 mol 氟化钠与 1 mol 氟化铝结合而成,在常温下呈现白色固体。冰晶石中所含氟化钠摩尔数与氟化铝摩尔数之比就是所说的分子比。传统分子比测定方法[2]有晶型法、化学成分法、电导法以及X射线衍射法。但是这些方法不仅操作复杂,所用仪器设备在电解槽内高温下容易损坏,而且无法及时直接测定出分子比,也就不能真正的实时指导生产。

本文采用人工蜂群算法(Artificial Bee Colony Algorithm)优化的最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)、自回归循环神经网络(Autoregressive Recurrent Networks,DeepAR)以及高斯过程回归(Gaussian Process Regression,GPR)进行不同时间窗口的分子比预测,最终通过线性回归模型将多个分子比预测值加权得到最终预测结果。同时应用传统支持向量机回归,传统最小二乘支持向量机回归等模型在相同数据集上开展平行实验,验证集成算法在铝电解分子比预测上的性能。

1 研究综述

工艺生产中,基于监控与数据采集系统获取大量数据中包含丰富的工艺过程历史信息,这些信息能够反映工业过程具体运行情况和出现的问题,反映某个或某些指标伴随着时间动态变化趋势。工业领域由于涉及多种体系结构及过程,产生的数据种类存在形式多样。其中,时间序列[4]就是工业过程中产生的一系列保存时序关系的结构化数据,它客观记录所监测系统在各个时刻点的重要信息。时间序列预测就是基于工艺过程中产生的时间序列数据对过程中某些关键变量进行预测,通过易测过程量推断难测过程量,从而了解过程趋势,正确评估系统当前状态,实现过程指标检测等,改善过程质量,提高管理效率和管理水平,使得整个过程的经济效益最大化,提升生产过程的整体可观可控性,为后续操作提供指导信息。

目前,参数时间序列预测[5]是铝电解工业中主要研究方向之一。利用时间序列模型可以对历史时序数据中的统一规律进行分析,并进一步预测趋势。及时高效地预测可以为后续的专家决策提供支持。

近年来铝电解生产实践研究表明,降低分子比是提高电流效率的有效途径之一。然而,当前有关电解过程中分子比测定主要采用人工取样分析,例如肉眼观察法、指示剂检查法、晶形光学法、热滴定法、硝酸钍滴定法等。上述方法各有各自的优点,但在满足现代化工业生产批量快速检测要求方面有待提高[7]。针对这一难题,人们通过机器学习等方式开始对分子比进行研究与预测。其中,2005年任凤莲提出BP神经网络在分子比预报中的应用[6]:因为BP神经网络网络模型可以对多个变量的系统进行分析,不需要建立确定的数学模型且其拟合度与预报精度都满足实际应用需求;2010年高钢,曾水平等人提出了基于神经网络的铝电解温度与分子比的预测研究[8]:该文献中使用径向基函数神经网络进行预测并通过聚类法优化神经网络,但是随着槽龄和环境等因素的变化还缺乏在线学习模型来更新网络参数进而提高模型适应能力;2018年曾水平、王嘉利提出基于随机森林与神经网络的铝电解分子比预测[9]。

上述预测方法多数通过已知与分子比相关的影响因素进行单一时间尺度的时间序列预测,但实际生产中,时间序列预测无法收集到所有影响因子的数据,有时甚至没有任何历史数据进行支持。本文通过不同的时间尺度进行预测可以大幅度降低预测过程中因为数据缺失所造成的误差;将人工蜂群算法进行改进,提高模型收敛速度并且使得模型可以进行参数动态学习,进而提高其泛化能力;使用自回归循环神经网络进行概率分布预测,解决无法考虑到未来不确定因素等问题。

2 基于多时间窗口的铝电解分子比预测

基于多时间窗口的铝电解分子比时间序列预测模型的构建及性能评估的技术路线如图1所示,包括数据预处理,模型训练,模型预测及性能评估三个组成部分。

预测模型所用架构如图1所示。其基本思路如下:

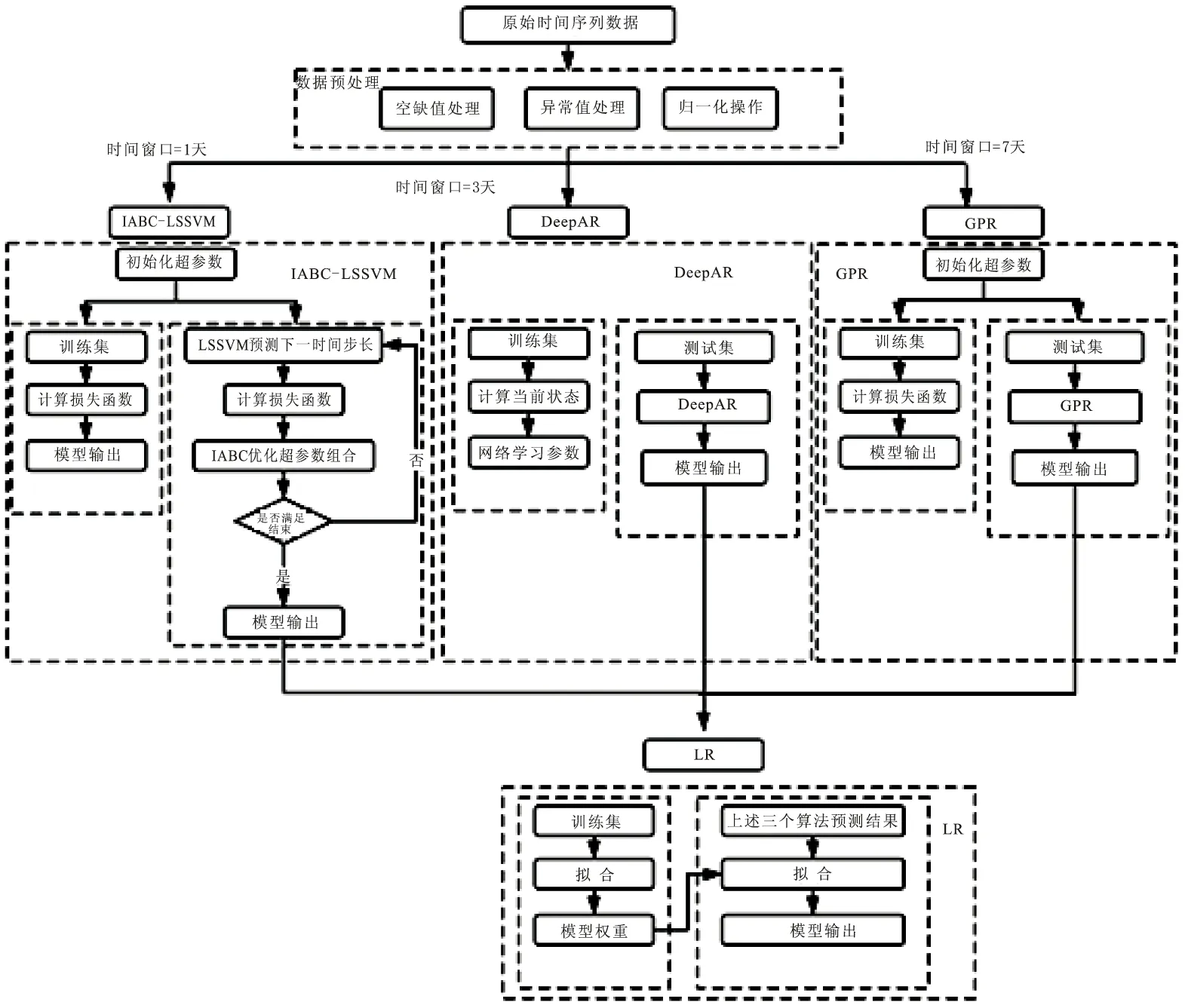
图1 基于多时间窗口的铝电解分子比预测架构图

将电解槽中产生的数据进行预处理:包括空缺值处理、异常值处理以及归一化操作;根据不同的时间窗口选择不同的预测模型进行分子比预测;对于最小二乘支持向量机模型使用改进的人工蜂群算法进行超参数的优化,实现超参数的动态学习,进而提高模型泛化能力;将上述三个时间窗口预测得到的分子比放入线性回归模型中,获得最终分子比预测值。

2.1 数据预处理

2.1.1 空缺值处理

对于数据缺失值超过半数的特征进行舍弃,其余特征缺失值采用线性插值法进行填充。线性插值法是一种时间序列数据补全方法,根据缺失数据前后的变化趋势情况,通过到相邻数据点的距离分配比重进行缺失值的补全。如公式(1)可得:

(1)

2.1.2 异常值处理

如图2、3所示,通过可视化分析,将小于Q1-1.5IQR或大于Q3+1.5IQR的值判定为异常值点,并将其修改为前后两日数据的均值。

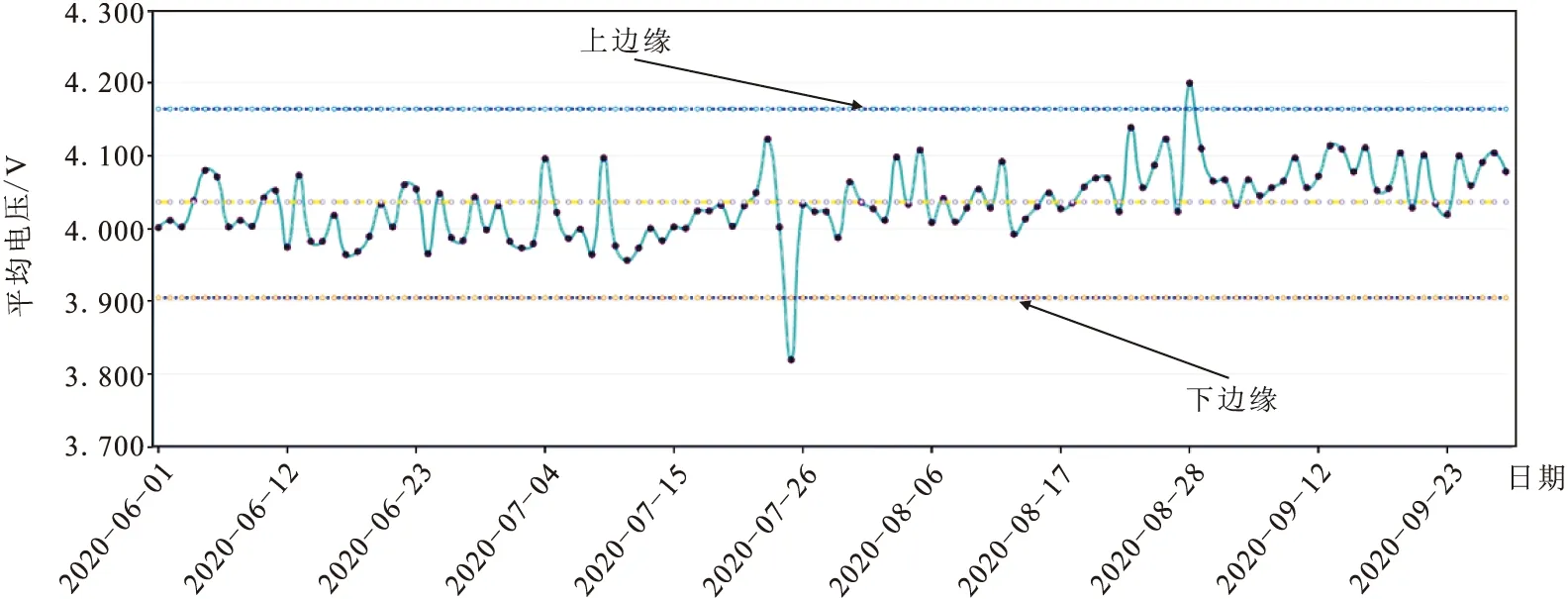
图2 某铝厂A电解槽中平均电压原始数据

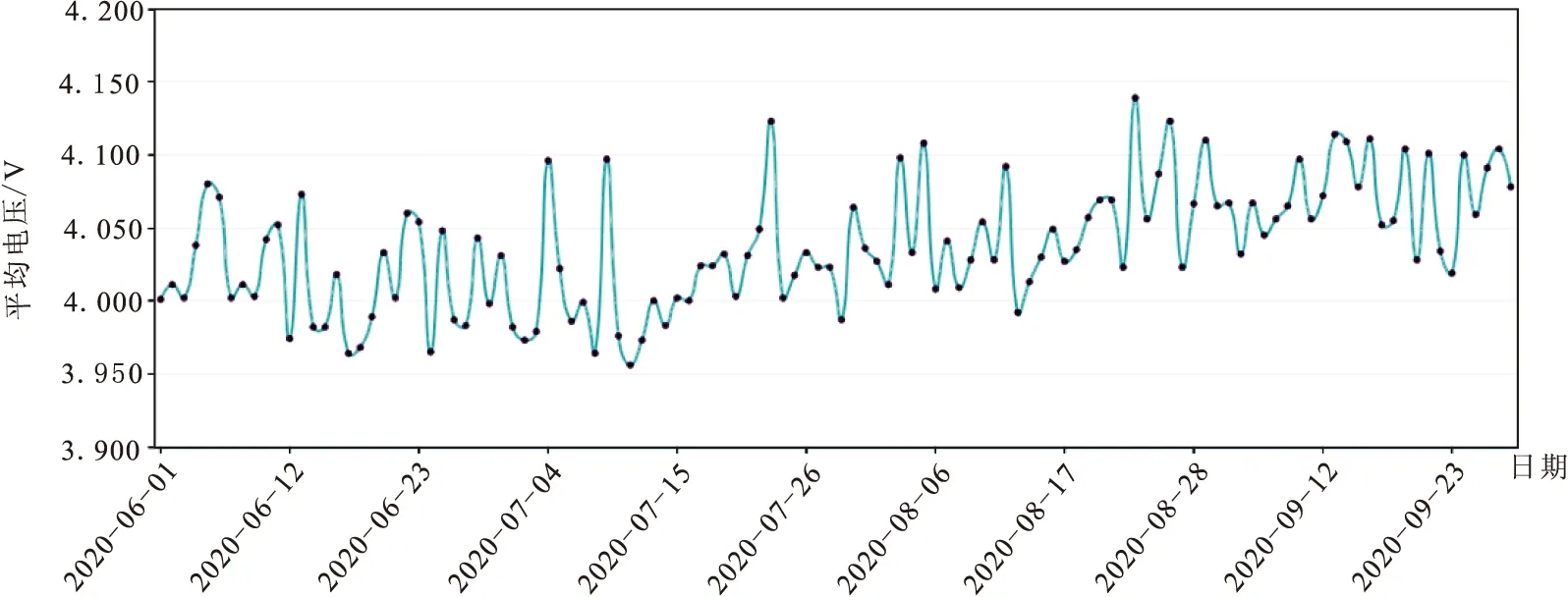
图3 A电解槽中平均电压异常处理后数据

2.1.3 数据归一化

由于电解槽中各特征量级不同且差异巨大,这对后续的预测过程影响较大,故采用min-max方法对数据进行归一化操作,将数据归一化至[0,1]之间,转换函数如公式(2)所示:

(2)

式中:max——样本数据中的最大值;

min——样本数据中的最小值。

2.1.4 特征提取

电解槽中影响分子比的参数分为四类:控制参数、化验参数、决策参数及测量参数。其中控制参数包括工作电压、设定电压、平均电压等;化验参数指铁含量、硅含量、镁含量、钙含量等;决策参数是出铝量、氟化盐添加量等;测量参数有铝水平、电解质水平、电解温度等。由于电解槽中各特征参数均满足时间序列要求,故各特征参数在成为预测模型输入之前需要进行时间序列的平稳性检验。

2.1.4.1 平稳性检验

平稳时序数据的统计规律随时间变化较小,通常可以用于时间序列预测。因此需要对数据集进行平稳性检验。本文采用单位根(ADF)检验得到数据平稳性评价结果,如表1所示:T假设检验值为-4.4,p-value表示t统计量对应概率值0.0003,1%、5%、10%信息准确值均大于检验值,证明不同程度拒绝原假设的统计值。同时p值小于给定的显著水平0.05,证明ADF检验的原假设是存在单位根。故极显著的拒绝原假设,认为该时间序列特征的数据平稳。若数据不平稳可以进一步通过差分法将时间序列数据转换为平稳的序列。如图4、5所示,是某参数原始时间序列图和对原始时序图进行一阶,二阶差分后效果图。

图4 某特征原始时间序列图

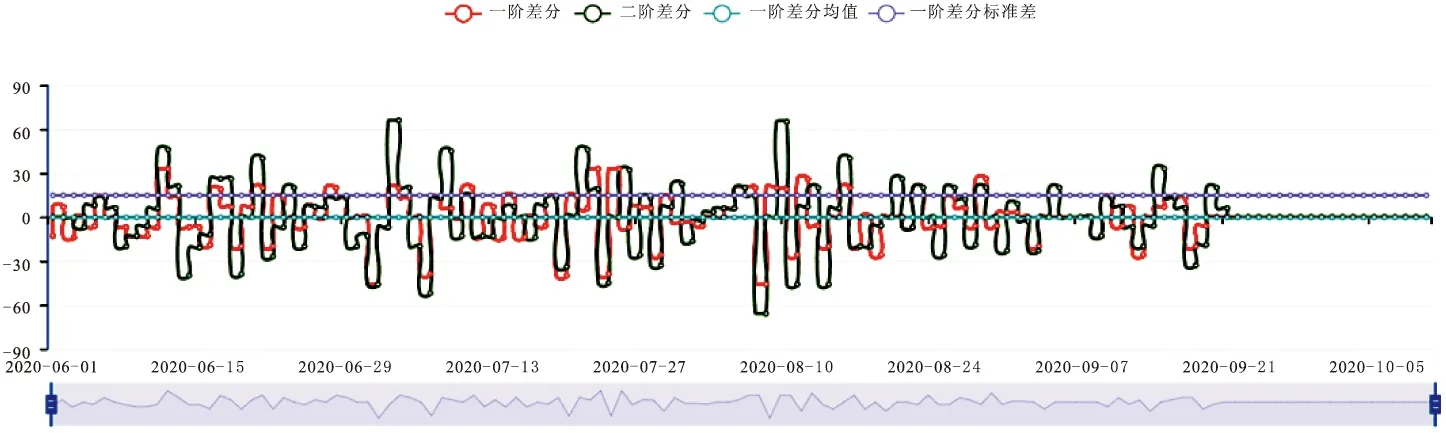
图5 某特征时间序列差分图

表1 某特征ADF检验相关信息

2.1.4.2 特征选择

实际工业生产中,影响分子比的参数很多且相互之间有着复杂的非线性关系,为了提高模型的预测精度,如图6所示,通过随机森林的方法进行特征的筛选,选择相关度最高的k个特征转化为适用于LSSVM的数据形式作为预测模型的输入,其中k由使用者自定义。

图6 特征选择效果图

2.2 模型训练

2.2.1 基于IABC-LSSVM预测模型

基于改进人工蜂群的最小二乘支持向量机预测模型(IABC-LSSVM)以时间窗口为1天进行构建,具体技术路线:将选中的特征数据放入已经人为设定好的初始化LSSVM模型中,进行后一天分子比的预测;得到预测值后,将预测值与实际值的均方根误差函数作为改进人工蜂群算法中的目标函数;将目标函数放入IABC中进行最小化,同时找到对应的当前最优超参数组合。用此最优超参数替换原有超参数继续预测后续分子比,以达到预测模型动态学习[10]的效果,进而提高模型的泛化能力。

2.2.1.1 最小二乘支持向量机(LSSVM)模型

LSSVM[11]将SVM中的不等式约束转化为等式约束,在采用误差平方和损失函数代替SVM的二次规划方法的基础上,将二次规划问题转化为线性矩阵求解问题。具体原理如下:

给定一组数据集(xi,yi)i=1,2,……,N,xi为第i个样本的输入向量,yi为对应输出,N为数据集所包含的样本数,通过非线性映射φ(x)将样本映射到高维空间,如公式(3)所示:

y(x)=ω·φ(x)+b

(3)

式中:ω——权值向量;

b——偏置向量。

按照结构最小化原理,LSSVM模型可表示为:

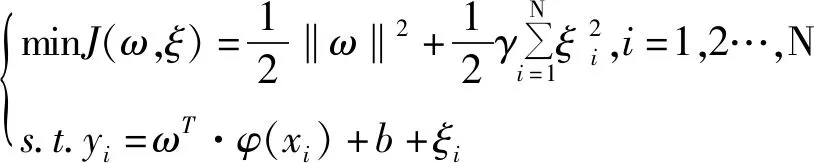
(4)

式中:γ——大于0的惩罚系数;

ξi——误差。

在求解该最小化问题时,加入一个拉格朗日因子φi,构成拉格朗日函数,并利用KKT条件,将LSSVM回归问题转化为:

(5)

其中:K(x,xi)=φ(xi)T·φ(xi)为满足Mercer条件的核函数。

与此同时LSSVM的泛化性能不仅与训练样本和测试样本有关,还取决于模型超参数的选择。

2.2.1.2 超参数优化

研究表明,超参数是影响LSSVM预测性能的主要原因[12]。其中核宽度主要影响样本数据在高维特征空间中分布的复杂程度,而正则化参数的作用是在确定特征空间中调节最小二乘支持向量机的置信范围以及结构风险比例。正则化参数C表示对误差惩罚度大小:随着C增大,误差的惩罚能力将逐步提升,预测误差与训练误差都将大幅降低,但训练时间会变长。核宽度则反映支持向量间的相关程度:核宽度过小,向量间影响小易导致泛化能力差;而核宽度过大易造成模型欠拟合,导致预测精度低。而SVM与神经网络不同,其训练过程相对容易,且没有局部最优,可以较好地使用高维数据,但其弱点是需要一个好的核函数[12]。因此使用人工蜂群算法优化正则化参数C与核宽度参数σ2两个超参数,将二者作为一个输入组合,以每一时间序列时刻的均方根误差作为适应度函数,通过反复迭代寻优,找到使得适应度函数最小的取值组合。

为了提高算法的收敛速度,改善传统人工蜂群[13]陷入局部最优解的问题,引入类似禁忌搜索算法思想,使用改进的人工蜂群算法(IABC,Improved-ABC),如图7所示:创建一个记忆表。使得ABC算法在每一次迭代过程中得到的局部最优解存放入列表中,当经历过limit次循环后某一个当前最优解依然没有发生变化,需要随机产生新解时,遍历记忆表中所有保存的记录,确保随机产生的新解从未出现过。本文构建的IABC-LSSVM(Improved-ABC-LSSVM)主要由最小二乘支持向量机与人工蜂群优化算法两部分组成。将预测数据集输入到LSSVM模型中,得到第一天分子比预测值,将预测值与实际值的均方根函数作为目标函数值放入人工蜂群算法中进行最小化计算,得到当前状态下最优的LSSVM超参数组合,将寻得超参数值替换LSSVM中原始值,继续进行下一天的分子比预测,如此反复直至完成整个时间范围内的预测过程。整个算法流程如图8所示。

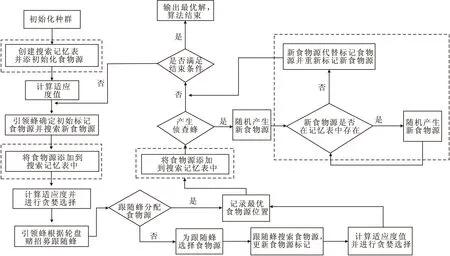
图7 IABC算法流程图

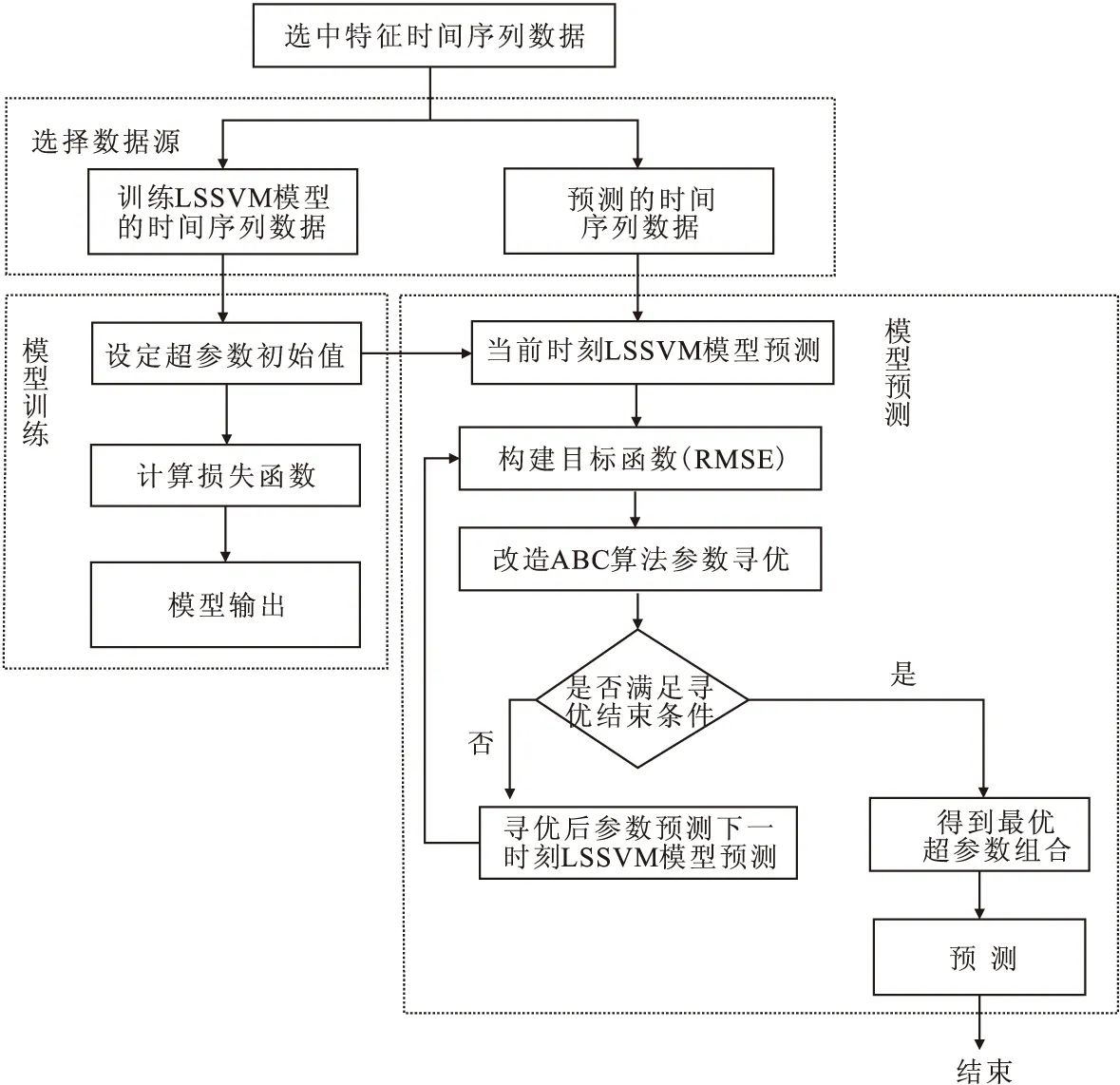
图8 IABC-LSSVM算法流程图

2.2.2 基于DeepAR的预测模型

自回归循环神经网络(DeepAR)是Amazon于2017年提出的基于深度学习的时间序列预测算法,通过循环神经网络(RNN)结合自回归来预测一维时间序列。大部分实际应用生产中,会有跨一组具有代表性单元的多个相似时间序列。DeepAR会根据多个相似时间序列利用深度循环神经网络学习不同时间序列内部的关联特性,使用多元或多重目标个数来提升整体预测准确度。算法最终产生一个可选时间跨度的多步预测结果,其中单时间节点预测为概率预测,默认输出P50,P90两个值。

数据往往是时间序列预测工作负载最大的问题。例如无法收集预测信息的全部影响因素数据;又可能影响因素在未来具有不确定性;或只有少量甚至没有历史数据。而相比较基于LSSVM等传统算法的时间序列预测性能,DeepAR的预测有着独特的优势:它能够在一定程度上减轻对数据的依赖性。作为一种监督学习算法,该算法直接在模型内部进行缺失值填充,为数据处理过程节省大量时间。与此同时,利用DeepAR可以将多个时间序列相互关联,以便处理统计学中难以解决的非线性问题和规模问题。

算法模型训练(左侧)与预测(右侧)详细过程如图9所示。

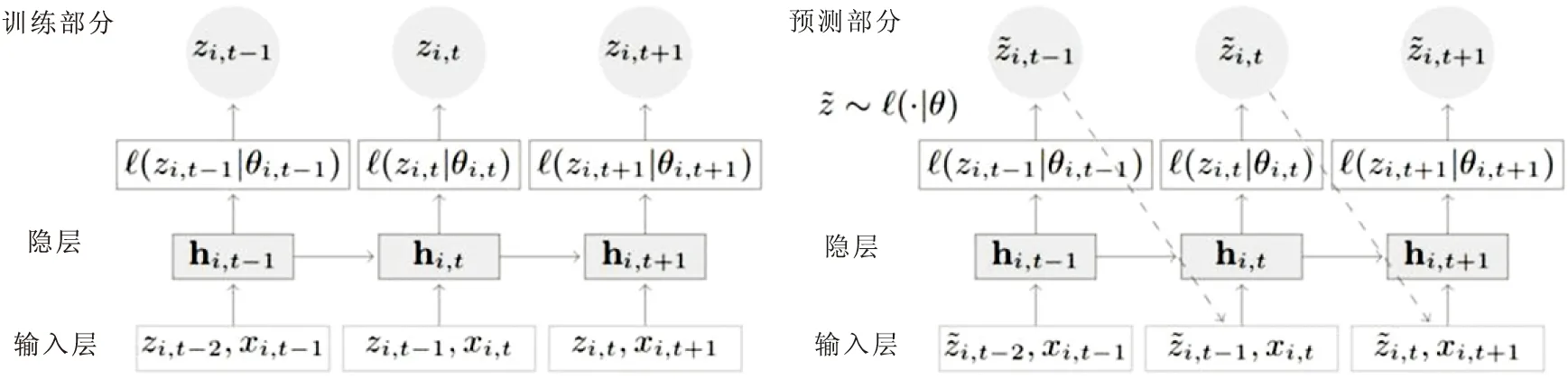
图9 DeepAR模型预测原理

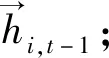
(6)

(7)

(8)

(9)

2.2.3 基于GPR的预测模型

上文中使用神经网络进行分子比预测,当单层神经网络节点数趋近于无穷时即在理论上趋近为高斯过程。同时GP模型是一种随机变量的集合,集合中任意数量的随机变量组合服从联合高斯分布,并且由均值函数和协方差函数唯一确定。其中协方差函数直接决定模型精度[15]。这就展示了深度学习中神经网络与高斯过程的密切联系,但不同的是高斯过程可以有原则地量化自回归循环神经网络中的不确定性。因为高斯回归在预测过程可进行概率推理的过程。

高斯过程回归[15]是从无数函数中找到任何符合测试数据的函数集,然后通过对先验信息的了解,不断缩小函数集寻找范围,最终通过贝叶斯法则的方法与高斯分布的性质相结合,计算得到函数集分布模型,根据建立好的模型对后续进行预测。它是一种基于统计学习理论与贝叶斯理论相结合的非参数模型,且完全由输入特征的均值函数m以及协方差函数k定义。在本文实验中,假设输入特征向量与分子比间关系f为高斯过程,即f～GP(m,k);输入向量xi服从高斯分布,则f(x)服从多元高斯分布f(x)～N(m(x),K)对训练集构建回归模型(公式10)。

y=f(x)+ε

(10)

(11)

式中:m(x)——多元高斯分布均值向量;

K——多元高斯分布协方差矩阵(公式11)。

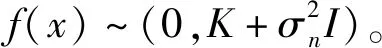
(12)

式中:K*=〔k(x*,x1),…k(x*,xn)〕,K**=k(x*,x*)。

根据多元高斯分布条件概率,计算得到f*的后验分布(公式13)

f*|X,y,X*～N(m(f*),cov(f*))

(13)

式中:X——训练集输入特征向量的列向量矩阵;

X*——预测集输入特征向量的列向量矩阵。

m(f*),cov(f*)分别计算得到的均值矩阵和协方差矩阵。

核函数作为整个高斯过程回归算法的核心,本文实验数据中特征向量与分子比间多为非线性关系,故选用径向基核函数。(公式14)

(14)

2.2.4 线性回归预测模型

根据上述三个不同时间窗口预测结果,把最终分子比预测值定义为因变量Y,与其相关性显著的因素定义为自变量,3个因素分别定义为X1(时间窗口为一天的分子比预测值)、X2(时间窗口为3天的分子比预测值)、X3(时间窗口为7天的分子比预测值)。令线性方程如公式15所示:

Y=α0+α1X1+α2X2+α3X3

(15)

式中:α0——常量;

α1、α2、α3——三个自变量相应系数,称为偏回归系数。

通过多元线性回归模型得到三个自变量对应权重值以及α0常量取值即可通过加权计算得到最终分子比预测值。

2.3 模型预测及性能评估

将预测数据集分别输入到IABC-LSSVM,DeepAR以及GPR预测模型中分别得到不同时间窗口对应的时间序列分子比预测结果。最后将三个不同分子比预测结果放入LR模型中进行加权预测,得到最终分子比预测值。本文采用均方误差(Mean Squared Error,MSE),均方根误差(Root Mean Squared Error,RMSE),平均绝对误差(Mean Absolute Error,MAE)对三种独立预测模型和最终线性回归模型进行性能评估,故公式(16～18)所示:

(16)

(17)

(18)

式中:yi——真实值;

m——预测样本的个数。

三个评价指标的值越小,表明模型的预测精度越高。为了更加直观地对比各个模型性能,本文选择基于相同的训练集和测试集分别进行计算,使用传统SVM、LSSVM模型对比IABC-LSSVM模型,从而形成对照算例。

将平稳后的数据集中所有特征进行归一化处理后,转化为适用于模型的数据形式,输入到各模型中。对于时间窗口为一天的预测模型:IABC-LSSVM,SVM以及LSSVM模型的惩罚项均设置为0.9,核宽度设置为0.3;时间窗口为三天的自回归循环神经网络设置其RNN网络层数为2,每层40个神经元,预测范围为十天,学习速率0.002,迭代20次;时间窗口为七天的高斯过程回归则设置初始化学习速率0.2,sigma为0.5。拟合效果图如图10～13所示。其中传统的支持向量机模型对于分子比值波动趋势的捕捉精确度欠缺,通过IABC-LSSVM预测模型不仅仅提高了人工蜂群寻优的效率同时更加精准地抓住分子比动态变化趋势;DeepAR算法中较细的预测折线代表预测的中位数,深色阴影区域为50%置信区间范围,浅色区域为90%置信区间范围。从预测结果图中可以直观地看出大部分实际值落在50%置信区间中,并且全部处于90%置信区间预测范围内;GPR模型中蓝色折线表示训练集,黄色则代表测试集,而红色散点为测试数据集在高斯过程回归模型中得到的预测结果;LR回归模型中,将三个不同时间窗口的时间序列预测结果合成为最终预测值,其预测曲线与实际数值趋势变化大体一致,拟合效果较好。将2020年6月1日至2020年9月30日的数据作为训练集,预测2020年10月1日至2020年10月10日共计10天的分子比,结果如表2,3所示。时间窗口为一天,三天的预测评估指标中RMSE分别约为0.29和0.24,表明预测结果较好,时间窗口为7天的测试RMSE约为0.25,表示GPR模型对于高维特征的预测具有一定的波动,对结果有一定的影响。最终线性回归预测结果的均方根误差为0.25。

表2 不同时间窗口预测模型结果

图10 传统机器学习模型与IABC-LSSVM对比图

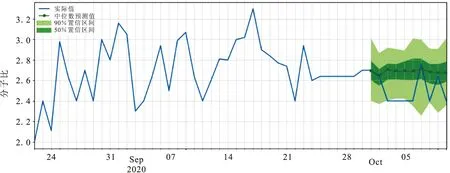
图11 自回归循环神经网络预测效果图

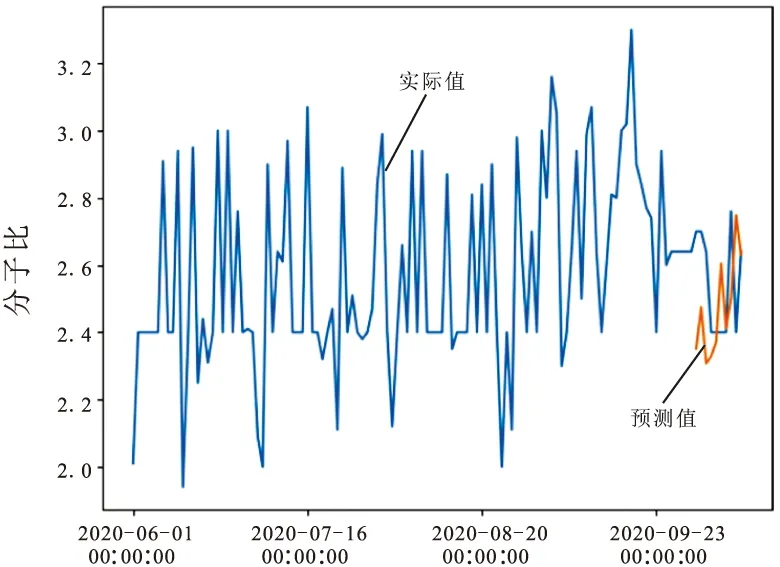
图12 高斯过程回归预测效果图

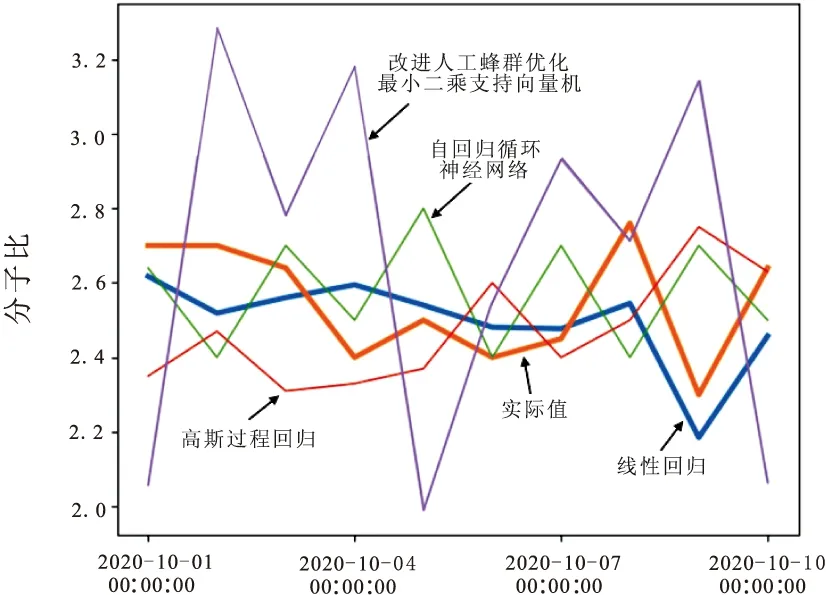
图13多元线性预测效果图

表3 不同时间窗口预测效果对比

3 结 论

本文采用IABC-LSSVM、DeepAR、GPR模型对不同时间窗口分子比进行预测,后通过LR模型进行回归分析实现铝电解中分子比的预测,应用国内某铝厂电解槽2020年6月1日至2020年10月10日已有各项相关因素以及分子比数据进行时间序列分析。结果表明,将不同时序窗口分子比预测值进行多元线性回归后得到的分子比能够较好地预测所需要的变动趋势以及大致结果。与传统机器学习回归模型相比较,基于人工蜂群改进后的LSSVM算法、基于循环神经网络的自回归神经网络以及GPR算法的LR模型RMSE更低,预测结果较好。

本文使用不同时间窗口进行分子比的加权预测,研究结果预期可以为提高电解槽电流效率等工作提供帮助,为后续出铝量等工作提供决策支持依据。本文在对分子比进行预测时,构建的模型中相关特征主要包括铁含量等相关因素的传统时间序列特征,结果虽优于多数模型,但考虑时序特点不够全面。在未来工作中,将结合更多铝电解工艺中的流程特征,对不同的影响因素提取其对应分子比独特的时间序列特征进行进一步预测分析。