基于车桥耦合理论的梁式桥阻尼比识别研究1)

阳 洋 *, 许文明 *, 卢会城 *, 袁爱鹏 *, 谭小琨 *, 毕和生 ** 方光俊 **唐 艳

* (重庆大学山地城镇建设与新技术教育部重点实验室,重庆 400030)

† (重庆大学土木工程学院,重庆 400030)

** (中国电建集团重庆工程有限公司,重庆 400060)

†† (重庆高新开发建设投资集团有限公司,重庆 400039)

引言

梁式桥阻尼比既是桥梁结构动力响应的重要因素,也是桥梁健康监测的重要参数,其取值大小直接影响梁式桥动力响应及健康状况,但其测试机理及实测技术方面仍然落后于其他研究,严重制约着动力响应计算及健康状况评估[1-5].

现阶段获取梁式桥阻尼比的主要方法是通过直接布置在梁式桥上的传感器获取梁式桥振动信号的直接测试法,并通过各类信号分析方法来识别梁式桥阻尼比.Mclamore 等[6]对Newport 桥进行长期监测,利用随机振动理论和功率谱密度法估算了该桥的频率、第一阶振型和阻尼参数.文献[7]基于梁式桥上传感器历史数据,利用蒙特卡罗模拟和灵敏度分析了第一阶振型和阻尼比置信区间,并指明阻尼比不唯一.Magalhaes 等[8]使用协方差驱动的随机子空间识别方法,在传感器正常运行期间内根据其测量的梁式桥响应对结构阻尼等模态参数进行估算识别.Li 等[9]利用大型桥梁健康监测系统传感器数据进行长期的统计分析,采用贝叶斯谱密度算法推理估计梁式桥阻尼比等模态参数.关孝文等[10]以一座钢混叠合简支梁桥为工程背景,采用理论与试验对比的方法,建立该桥有限元模型,并通过行车激励的方式,测试梁式桥的自振频率、振型及阻尼比,从而对该桥的动力性能进行评估.徐绪绪[11]对某公路梁式桥多组实测动位移、加速度信号采用波形分析法分别求取阻尼比,探讨实测阻尼比值的随机性及两种信号求解结果差异.秦世强等[12]以预应力混凝土连续梁桥为例,研究工作振型分析中识别的阻尼比离散性问题,分析了频域、时域和时频分析梁式桥阻尼比识别方法的不确定性.孙倩等[13]构建响应功率谱传递比(PSDT)函数,并利用PSDT 在系统极点处的重要特性建立PSDT 驱动的峰值法;基于PSDT 驱动的最小二乘复频域法(LSCF),通过参数化拟合思路识别频率、振型和阻尼比.除了阻尼比测试离散性问题,上述直接测试也存在测试安装调试费时费力等不利因素.

基于直接测试的不足,文献[14-18]基于车桥耦合动力学理论提出非直接测试的扫描测试频率法,即测试车辆在梁式桥上运行,通过运行下的测试车辆上传感器采集信号进行梁式桥频率扫描识别,在采用间接测试方法的基础上,McGetrick 等[19]从测试车辆采集信号得到的加速度频谱图中分析梁式桥阻尼比,发现当存在路面粗糙度时阻尼比的识别结果较差.Gonzalez 等[20]提出了基于模型升级迭代法的双自由度检测车车体响应识别梁式桥阻尼的六步算法,但该方法需要假定桥梁的弹性模量、惯性矩和质量等过多桥梁参数,且需要建立理论模型去优化阻尼值.Keenahan 等[21]使用卡车-拖车车辆理论模型模拟系统,基于安装在拖车车轴上的加速度传感器,监测梁式桥阻尼值的变化.Yang 等[22]通过安装于两轴移动检测车辆上的多个加速度传感器和位移传感器所测信号获取轮胎与桥面接触点信号来测试梁式桥阻尼比,但这种方法需要布设多个传感器来保证测试精度,试验测试操作便利性和经济性较差.基于间接测试技术的优势,梁式桥阻尼比的识别研究一直是其热点及难点问题,但是上述识别桥梁阻尼的间接测试方式具有设置参数过多,识别效率和操作便利性较低,且基于车桥耦合理论模型进行优化,考虑影响因素较少而理论模型与实测情况相比相差较大,同时缺乏试验验证影响测试精度等系列问题.

基于上述分析,结合文献[23-28]通过分析阻尼对于桥梁模态识别的影响,表明在测试过程中,桥梁阻尼与所得模态振型最大值位置有一定关系.本文提出了一种提取桥梁阻尼的间接测试技术新方法.相比于前述文献,该方法具有设置参数较少、操作简单方便、且具有更高测试精度等特点.首先基于车桥耦合动力学理论推导了有阻尼梁式桥采集信号与无阻尼梁式桥采集信号相关关系,并进一步提出了识别梁式桥阻尼比的基本步骤;然后基于动力学理论模型研究了不同车速与非恒定车速、路面粗糙度、环境噪音等不确定因素下新方法的适用范围;并通过实桥试验对该方法进行了初步分析,以期能够达到更加简单和准确地识别梁式桥阻尼比的目的,并为车桥耦合动力学理论技术在梁式桥模态参数识别在实际工程应用提供理论基础.

1 理论基础

1.1 理论推导

在图1 中,距离为ΔL的测试车辆和牵引车以恒定速度v在桥面上行驶.牵引车和测试车辆简化为支撑在其上的运动弹簧质量mv2和mv1,刚度为kv2和kv1,在文献[17-18]的理想车桥耦合模型下增加阻尼系数为cv2和cv1.总长度L,每单位长度的质量为m*,由于本文研究的模型基于最简单的简支梁模型来做的,因此选取的梁截面为均匀截面,弯曲刚度为EI,假定梁式桥在测试车辆到达之前处于静止状态.

图1 双车桥耦合动力学理论简化模型Fig.1 Simplified model of double vehicles-bridge coupling dynamic theory

该车桥耦合动力学理论的运动方程为

假设牵引车辆和测试车辆质量mv2和mv1远小于梁式桥的质量,即mv1≪m*L和mv2≪m*L,通过将式(6)代入式(3),乘以 s in(nπx/L),并从0 到L积分,然后根据正弦函数的正交条件,梁式桥结构的第n阶振型平衡方程为

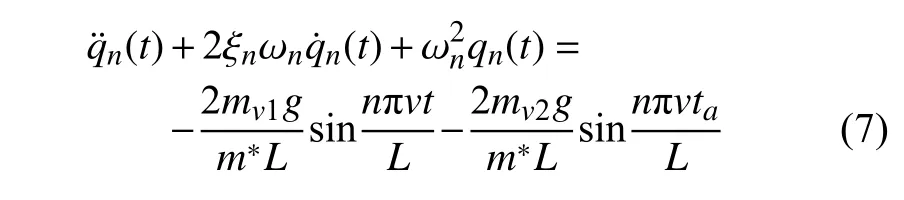
其中,ωn是梁式桥的第n阶角频率

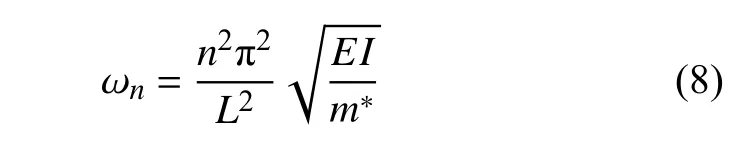
对于零初始边界条件,可以从式(7)两次积分获得梁式桥第n阶振型对应的广义坐标qn(t),其中A,B,C和D为结构参数,参数值见文献[29].

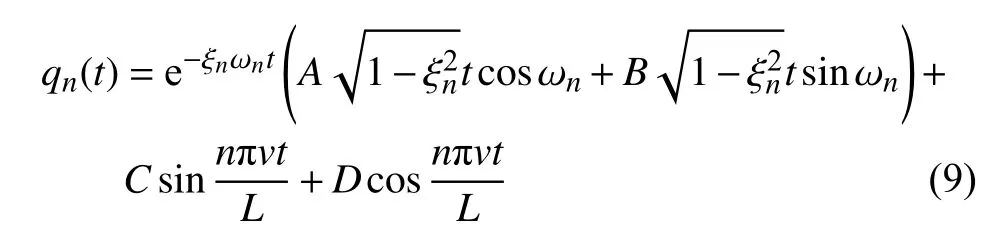
再从桥的位移响应中通过车桥耦合动力学原理带通滤波分离出测试车辆的位移响应分量[23-24],即与梁式桥第一振动振型相关的测试车位移响应分量R1为

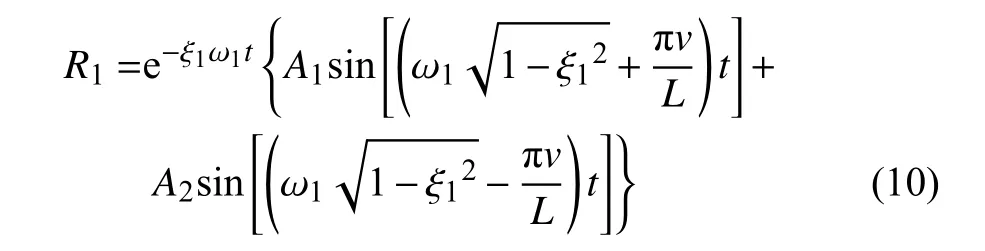
其中A1和A2为

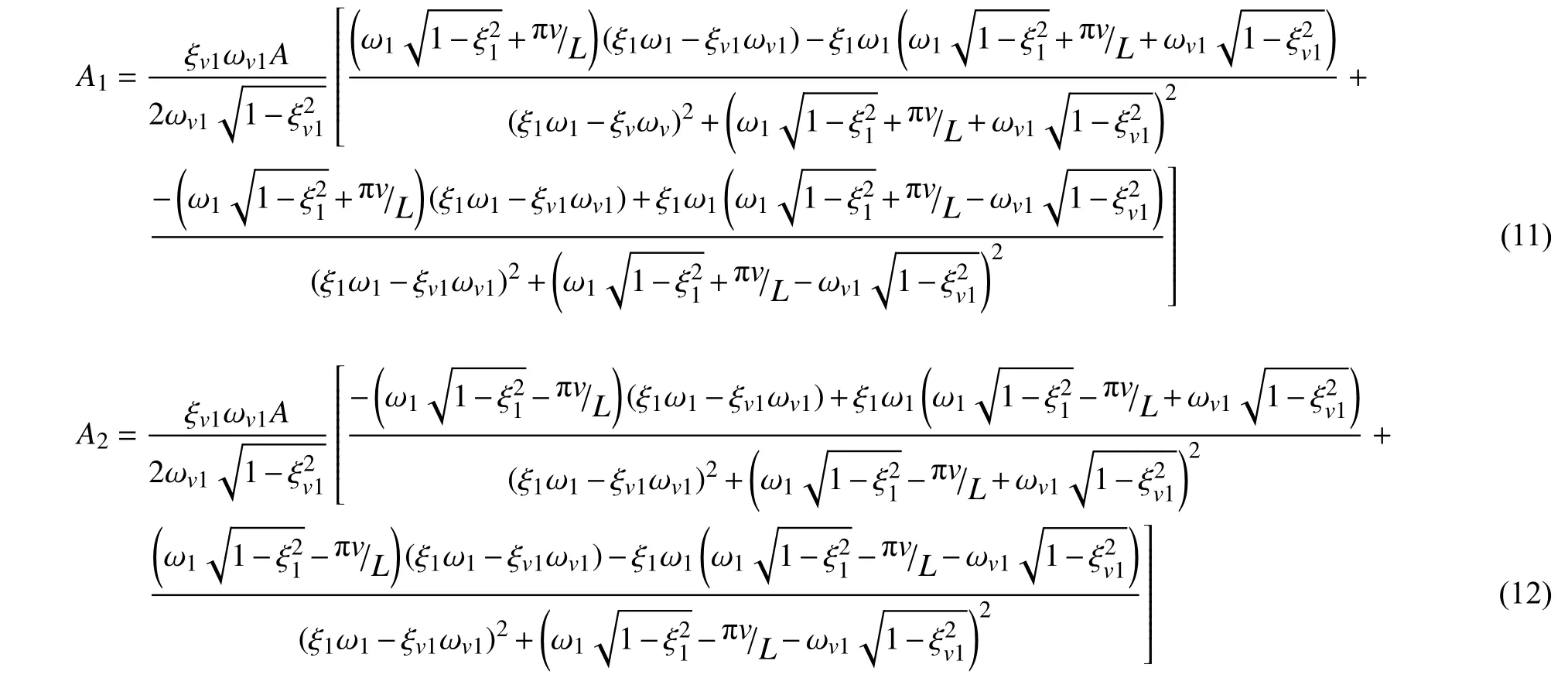
相应的梁式桥第一阶振型对应的测试车加速度响应分量也可以通过下式获得

应注意,车辆和桥梁的所有变量在式(16) 和式(17)中是常数.说明对于恒定的车速来说,系数A1至A2也是定值.式(17)中的车辆响应分量R11,可以通过希尔伯特变换等信号分析方法提取桥梁模态.

以希尔伯特变换为例

可以得到瞬时振幅

对A(t) 求导可得

由以上理论分析可知,当 ξ1较小时,有梁式桥阻尼和梁式桥无阻尼之间的关系近似为式(26).基于此,可以通过假定阻尼比值 ξ2反演模态,反复试算使模态峰值点位于中点位置,从而得到接近真实的阻尼比值,基于上述理论即提出一种全新的一阶梁式桥阻尼比值识别方法.

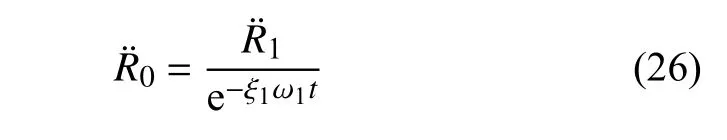
此外,从梁式桥第一阶振型的加速度响应分量中可看出,加速度响应中 ω1与附加质量m大小相关,为了研究附加质量对桥梁模态影响,进而影响阻尼比的识别,因此,本文进行了关于改变附加质量m的大小对桥梁振型模态识别影响的模拟分析.

图2 为不同车辆质量下桥梁一阶振型识别图,从图中可以看出,随着质量的增大振型变化不大,图3 为不同车辆质量下桥梁各节点位置模态与标准模态之差与标准模态的比值(误差),从图中可以看出,随着质量增大,振型识别误差在逐渐变大,但是误差最大为0.017,仍然较小,对于该方法的识别精度影响很小,由以上分析表明,附加质量m的增大能够增大该方法对于振型识别的误差,但是误差相对较小,不影响桥梁模态识别结果.本文采用的附加质量属于小误差的范围,不影响结构模态精度识别.

图2 不同车辆质量一阶振型识别图Fig.2 First order vibration mode identification diagram of different vehicle masses

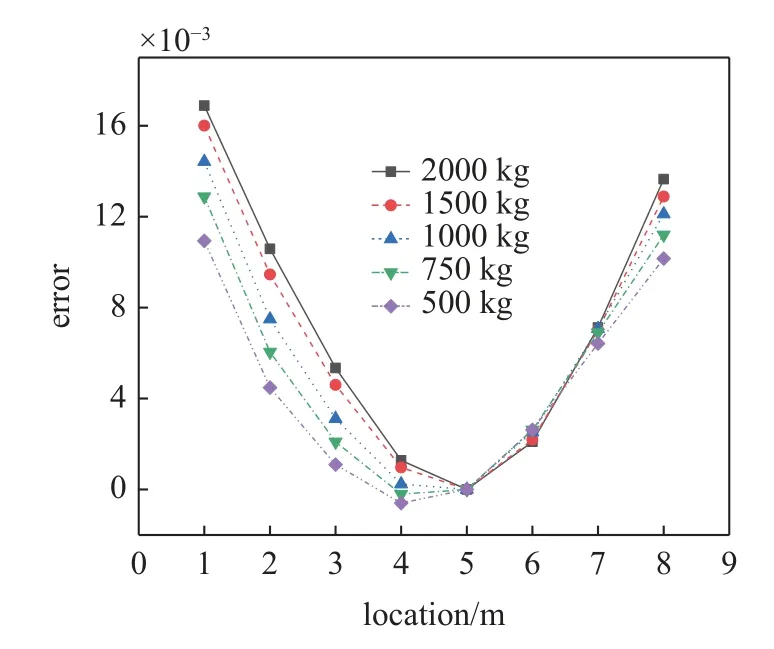
图3 不同车辆质量节点位置振型与标准振型态误差分析图Fig.3 Analysis diagram of node position mode and standard mode error of different vehicle masses

此外,本文提出的振型、阻尼比识别属于一种新方法,因此关于识别振型阶数选取方面也进行了初步模拟研究分析,分别同时对一阶和二阶振型进行识别.

从图4 和图5 中可得,一阶振型和二阶振型均可进行识别,且满足识别精度条件,但是一阶振型的识别效果明显优于二阶振型,其次,在桥梁振动分析中一阶频率对振型模态影响最大,随着阶数增大,影响逐渐变小,同时高阶模态不便于识别.基于上述情况本方法主要在一阶振型的基础上对其阻尼比进行识别.

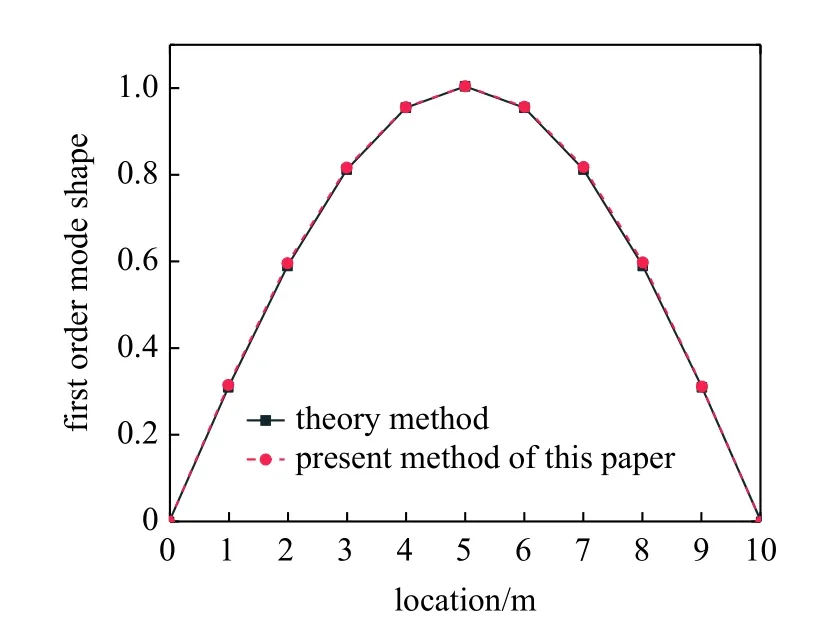
图4 基于车桥耦合动力学理论的桥梁一阶振型识别对比图Fig.4 Comparison diagram of bridge first-order vibration mode identification based on vehicle bridge coupling dynamics theory

图5 基于车桥耦合动力学理论的桥梁二阶振型识别对比图Fig.5 Comparison diagram of bridge second-order vibration mode identification based on vehicle bridge coupling dynamics theory

基于上述推导可知,上述理论公式均基于车桥耦合动力学理论中的测试车加速度信号演变推导而来,与牵引车的加速度响应信号无关,因此只需将测试车设计为车桥耦合动力学理论模型中的单自由度体系,通过测试车上的加速度传感器采集的信号分析即可.

1.2 方法流程介绍

由上述理论可知,以移动测试车按一定采样频率采集信号并反演测试车与梁式桥各接触点加速度响应信号;通过带通滤波器获取梁式桥一阶频率的加速度响应;假定某梁式桥阻尼比值,基于车桥耦合动力学理论获得梁式桥测试频率 ω1[18-19],则衰减系数 e-ξ1ω1t为与时间有关的变量;将上述滤波后的加速度响应除以该衰减系数,即可获得无梁式桥阻尼滤波后的加速度响应,进而通过短时频域分解法获取上述处理后信号第一阶振型[18];通过辨别该第一阶振型的最大值是否处于测试跨跨中,从而判断该假定阻尼比值是否为真实阻尼比,若第一阶振型的最大值未处于测试跨跨中,则重新假定阻尼比值,重复上述操作,直至第一阶振型最大值处于测试跨中点,其对应的一阶梁式桥阻尼比为最终识别值.本文方法与前述间接测试阻尼比识别方法进行对比,具有优势主要包含以下几个方面:首先,与文献[20]此类识别阻尼方法相比,本文的方法不需要预设参数,只需要按照图6 流程调试假定的阻尼比值,设置参数少;其次,本文方法是采用车辆运动方式采集信号,且只需要单辆单自由度检测车和对应的单个传感器简单组合且呈现力学显式关系,与文献[22]此类需要布设多个传感器且车体相对设计繁琐和方法逻辑相对复杂相比,本文方法更简单便捷.最后,本文方法仅采用一阶振型,且一阶振型相对于其他阶振型更容易获得、精度相对更高,以及考虑更多的实际环境影响因素,且进行实桥测试验证,具有更高的测试精度.

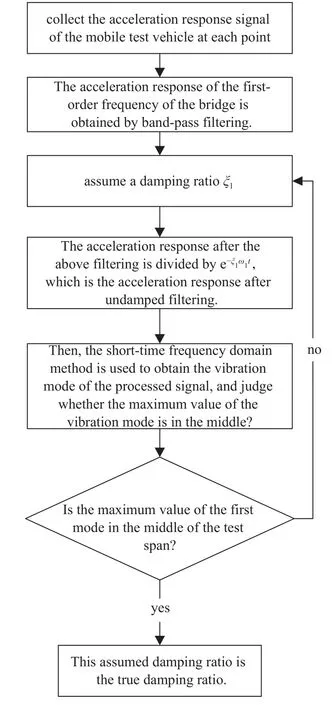
图6 阻尼比识别方法流程图Fig.6 Flow chart of the damping ratio identification method

2 车桥耦合动力学模型分析

为了使本文方法更贴近于实际测试情况,考虑了多种测试时的环境因素,首先考虑无粗糙度、无外界影响因素下该方法的适用性.选取重庆涪陵夏成线李子湾桥模型,梁式桥测试跨桥长30 m,截面惯性矩Ix=0.79 m4,弹性模量E=3.25 × 1010N/m2.

基于车桥耦合动力学理论利用短时频域分解法提取模态时,将简支梁测试跨分为10 个单元,分别为E1～ E10,如图7 所示,其余数字为单元节点编号,即j=0,1,···,10,而本文得到第一阶振型的节点为1～ 9,节点0 和10 为测试跨模型入桥和出桥的位置.

图7 梁式桥模型中单元、节点编号Fig.7 Number of elements and nodes of bridge model

结合文献[27-29] 前期研究,选取牵引车质量1500 kg,刚度为15 kN/m,阻尼为200 N·s/m,测试车体质量1000 kg,刚度为20 kN/m,阻尼为100 N·s/m,采用车速恒定为1 m/s,采样频率为100 Hz,已知动力学模型中梁式桥真实阻尼比为0.01,由于文献[30-32]表明MATLAB 模拟车桥耦合动力学模型时获得的时域信号与ABAQUS 模拟时获得的时域信号基本一致,且效率远高于采用ABAQUS 模拟,因此本文主要采用MATLAB 模拟的车桥耦合动力学模型获得加速度信号.

利用上述车桥耦合动力学模型按照图6 框架流程方法计算的模拟结果如图8 和图9 所示.图8 是行驶在梁式桥上的测试车,基于车上的传感器以100 Hz 的采样频率获取的加速度时域信号图,然后通过车桥耦合动力学理论带通滤波器滤波,获取梁式桥一阶频率的加速度信号.如图9 所示,假定某一梁式桥阻尼比值,则衰减系数 e-ξ1w1t为与时间有关的变量,利用上述滤波后的信号除以该衰减系数得到图10 信号图,同时采用短时傅里叶变换获取图11 第一阶振型图,由图10 和图12 信号可知,与无阻尼梁式桥滤波信号相比,前20 s 信号基本吻合,后10 s 信号拟合结果较差,这也导致图8 第一阶振型在尾部出现失真现象,主要由于梁式桥阻尼存在导致后10 s 信号中梁式桥基频信息衰减殆尽,相除后的尾部信号已失真,识别的振型尾部已无意义,此时可采用测试车分别从梁式桥两端各自出发通过梁式桥,提取去除各自尾部信号进行对称融合做法获得第一阶完整振型,如图13 所示,当假定阻尼比为0.01 时,此时正好为真实阻尼比,第一阶振型最大值位于跨中,即图13 中横坐标位置5,且第一阶振型较为对称;当假定阻尼比偏离真实阻尼比,如0.009 2时,此时小于真实阻尼比,该振型最大值位于位置4,出现左偏现象;当假定的阻尼比为0.010 8 时,此时大于真实阻尼比,该振型最大值位于位置6,出现右偏现象;而当假定阻尼比处于0.009 3～ 0.010 7 之间时,该振型最大值均位于位置5,即测试跨跨中,此时不存在左偏右偏现象,可作为识别的梁式桥阻尼比区间,而此时真实阻尼比0.01 恰好处于该区间范围,识别的阻尼比区间两端与真实阻尼比存在偏差范围7%.表明了识别阻尼比与实际测试相似,具有一定离散型.

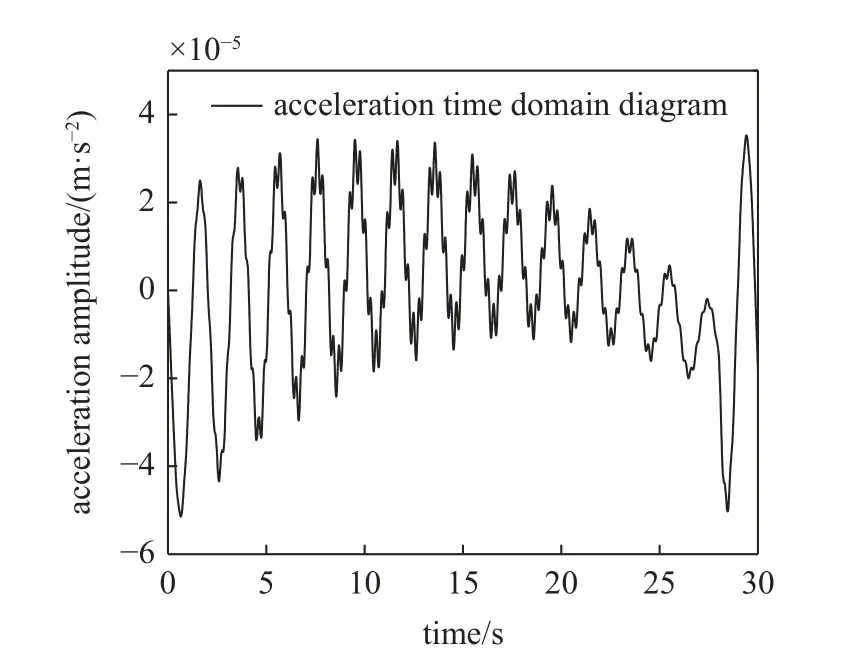
图8 加速度时域信号图Fig.8 Acceleration time domain signal diagram

图9 对采集信号滤波后的时域信号图Fig.9 Time domain signal diagram after filtering the collected signal

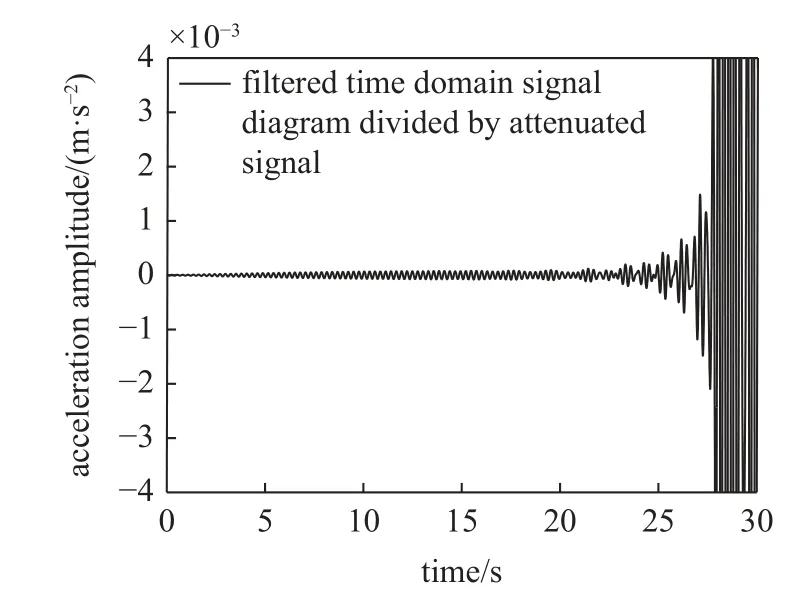
图10 除以衰减信号后的滤波时域信号图Fig.10 Filtered time domain signal diagram after dividing by the attenuated signal

图11 拟合第一阶振型图Fig.11 Fitting modal diagram

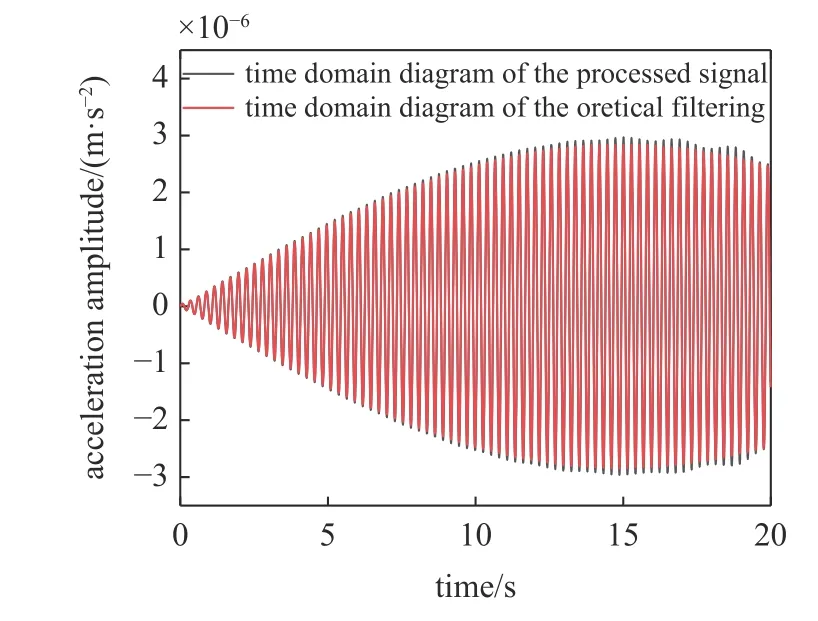
图12 处理后信号与无阻尼梁式桥振动信号前20 s 对比图Fig.12 Comparison between the processed signal and the no damping bridge vibration signal before 20 s

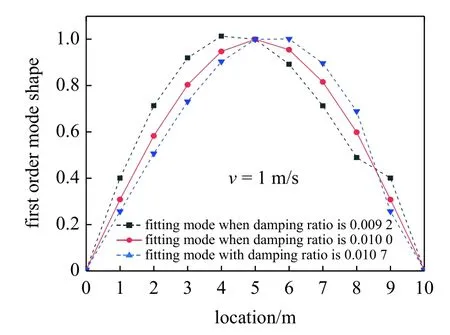
图13 第一阶振型拟合对比图Fig.13 Comparison of modal fitting

同理,基于理论和车桥耦合动力学模型分析表明,当真实阻尼比越大,由于,式(15)不成立,处理后的信号易失真,导致第一阶振型识别效果不佳.综合不同阻尼比下的车桥耦合动力学模型分析,真实梁式桥阻尼比不大于0.02 时,采用本文方法能有效识别梁式桥阻尼比.与表1 中各类梁式桥相关设计规范[33-34]的阻尼比取值范围相比,有一定适用范围.

表1 各类梁式桥阻尼比取值范围Table 1 Value range of various bridge damping ratios

在此基础上进行参数分析,结合文献[27-29]前期研究,本文考虑不同车速与非恒定车速、路面粗糙度、环境噪音等实际工程因素影响下分析该方法识别梁式桥阻尼比的可靠性.

2.1 不同车速与非恒定车速下的梁式桥阻尼比识别

为验证不同车速对该阻尼比识别方法的影响,本文基于真实阻尼比为0.01 时,然后假定不同阻尼比,改变车速为1 m/s,2 m/s,4 m/s,按图6 框架流程分别进行车桥耦合动力学模型分析,分析车速对该方法的影响.其中车桥耦合动力学模型分析参数与前述参数一致,即牵引车质量1500 kg,刚度为15 kN/m,阻尼为200 N·s/m,测试车体质量1000 kg,刚度为20 kN/m,阻尼为100 N·s/m,采样频率为100 Hz.不同车速下识别结果如图13～图15 所示.

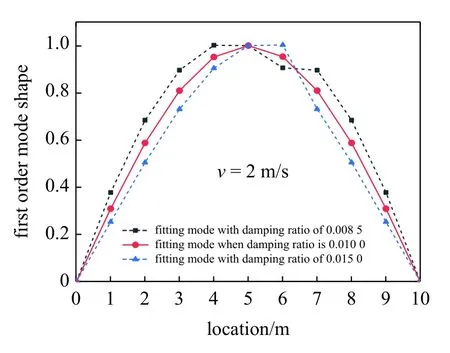
图14 v=2 m/s 下阻尼比识别结果Fig.14 Recognition result of damping ratio under v=2 m/s

图15 v=4 m/s 下阻尼比识别结果Fig.15 Recognition result of damping ratio under v=4 m/s

结果表明:当车速为1 m/s,2 m/s,4 m/s 时,如图13～图15 所示,假定阻尼比正好为真实阻尼比0.01 时,第一阶振型最大值都位于测试跨跨中,且该振型较为对称;车速为1 m/s,2 m/s,4 m/s 时的阻尼比识别区间分别为0.009 3～ 0.010 7,0.008 6～ 0.014,0.007 2～ 0.012 1,识别的阻尼比区间两端与真实阻尼比存在偏差范围分别为:7%,14%,28%.因此,当车速为1 m/s,2 m/s,4 m/s 时,都能有效识别梁式桥阻尼比,然而识别区间表明当车速为1 m/s 时,识别偏差最小、精度最高,因此采用最优车速1 m/s.

上述车桥耦合动力学模型分析得出车速为1 m/s 的恒定速度下梁式桥阻尼比识别效果最佳,然而在实际情况下,车辆的行驶速度可能会在1 m/s 左右变化,因此需要考虑车辆速度随机变化的可能性.在此基础上,确定车辆行驶速度变化范围在0.987 5 m/s～ 1.012 5 m/s 之间,如图16 所示,并按图6 框架流程进行动力学模型分析,分析非恒定车速对该方法的影响.识别结果如图17 所示.

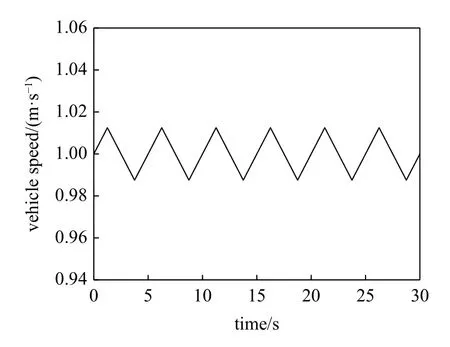
图16 非恒定速度变化历程Fig.16 Non-constant running speed time history

图17 表明:假定阻尼比正好为真实阻尼比0.01 时,第一阶振型最大值位于测试跨跨中,且该振型较为对称;识别的阻尼比区间为0.009 3～ 0.010 6,识别偏差范围为7%,而在这区间外的假定阻尼比识别结果会存在不同程度的左偏右偏.因此在该速度变化范围内,阻尼比识别结果与恒定速度相比仍能有效识别梁式桥阻尼比,且识别精度仍然有效.除此之外,根据文献[35]可知本文不须考虑车辆在1 m/s情况下的俯仰问题.

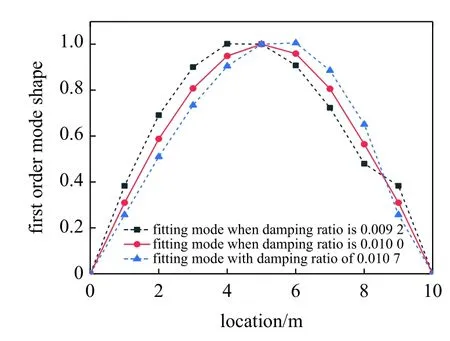
图17 非恒定速度下阻尼比识别结果Fig.17 Recognition result of damping ratio at non-constant speed

2.2 路面粗糙度影响下的梁式桥阻尼比识别

考虑路面粗糙度对车-双桥相互作用模型.其理论模型图如图18 所示.与图1 的唯一区别即增加桥面粗糙度r(x),其他模型参数与上述图1 参数一致.检测车和牵引车的平衡方程为

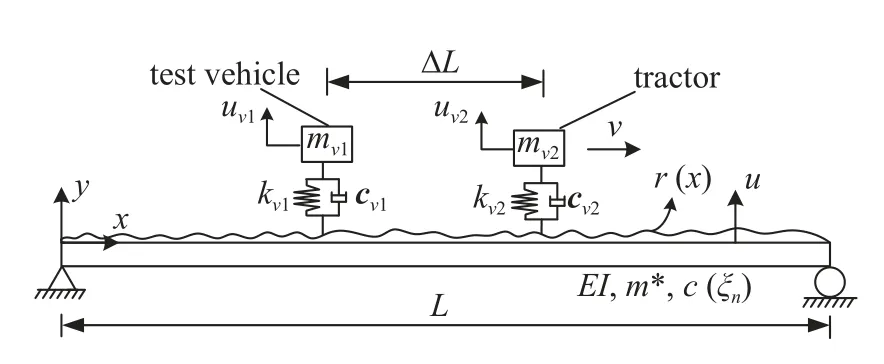
图18 考虑粗糙度的双车-桥相互作用模型Fig.18 Double vehicle bridge interaction model considering roughness

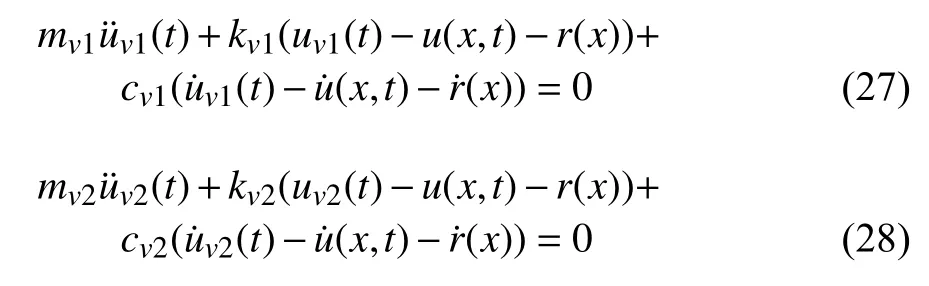
式(27)和式(28)与式(1)和式(2)的区别为每个式子在和刚度、阻尼有关的位置增加相应的粗糙度分量.其推导过程与上述一致,下面直接写出检测车响应分量结果

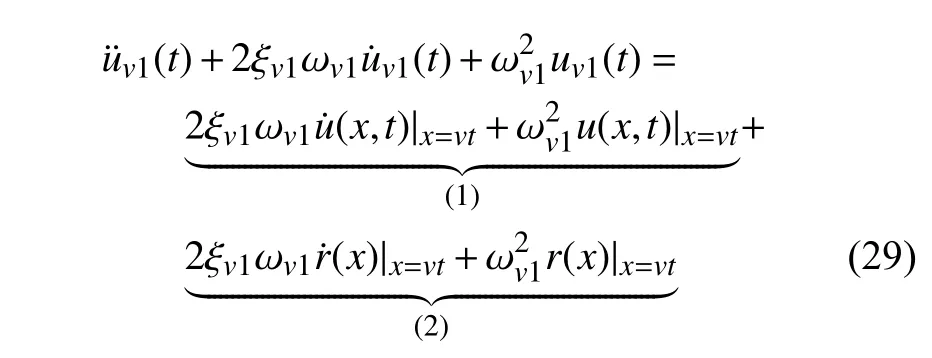
本文粗糙度采用ISO8608[36]所建议的功能密度函数来模拟.其功能密度函数如下所示

式中,n为每单位长度的空间频率,w为常数,n0为0.1 m-1和Gd(n0) 为位移功能密度函数值,由路面粗糙度等级确定.

各级粗糙度下的路面粗糙度位移振幅值d可表示为

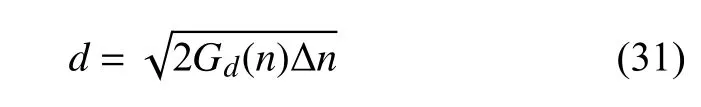
式中,Δn为空间频率的采样间隔.

接着以不同空间频率的余弦函数叠加来模拟路面粗糙度r(x),可表示为

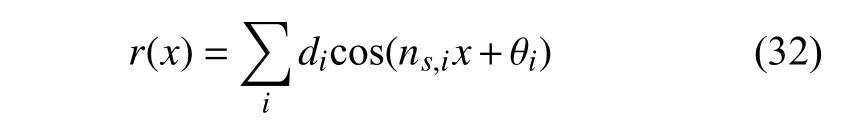
式中,ns,i为路面粗糙度的空间频率,di和 θi分别为路面粗糙度的幅值与随机相位角.

为研究在有路面粗糙度影响下梁式桥阻尼比识别效果,采用大小测试车,即两辆测试车分别从梁式桥某一端出发通过桥面,再对式(29)的信号进行信号相减方法降低路面粗糙度影响[25-26],其中牵引车质量1500 kg,刚度为15 kN/m,阻尼为100 N·s/m;大测试车质量2000 kg,刚度为20 kN/m,阻尼为60 N·s/m;小测试车质量1000 kg,刚度为10 kN/m,阻尼为30 N·s/m.并分别研究A 级和B 级路面粗糙度下梁式桥阻尼比识别结果.已知模型中梁式桥真实阻尼比为0.01,再假定一系列梁式桥阻尼比值按图6 框架流程识别真实值,如图19 和图20 所示.

图19 A 级粗糙度下不同假定阻尼比识别结果Fig.19 Identification results of different assumed damping ratios under A class roughness

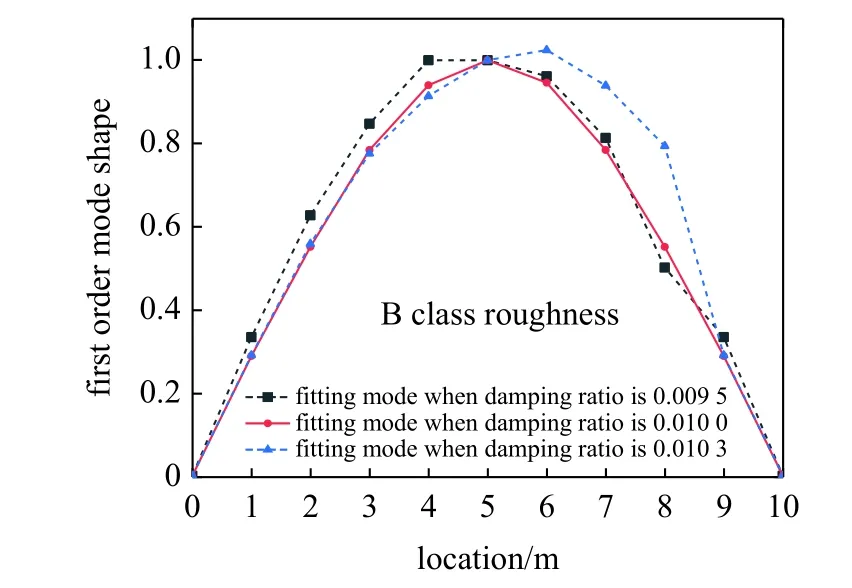
图20 B 级粗糙度下不同假定阻尼比识别结果Fig.20 Identification results of different assumed damping ratios under B class roughness

由图19 和图20 表明在A 和B 级路面粗糙度下,当假定阻尼比为真实阻尼比或者附近,第一阶振型最大值都位于跨中,而当假定阻尼比偏离真实阻尼比较大时,都会出现不同程度的左偏或右偏现象,即最大值不在第一阶振型中点.正如图20 所示,在B 级粗糙度下,当假定阻尼比为0.01 时,此时正好为真实阻尼比,第一阶振型最大值位于跨中;且第一阶振型较为对称;当假定阻尼比小于0.009 5 时,即会出现左偏现象;当假定阻尼比大于0.010 3 时,即会出现右偏现象;而当假定阻尼比处于0.009 6～ 0.010 2时,此时第一阶振型最大值均位于测试跨跨中,可作为识别的梁式桥阻尼比区间,而此时真实阻尼比0.01 恰好处于该区间范围,识别的阻尼比区间两端与真实阻尼比存在偏差范围4%.该区间较前述不考虑路面粗糙度及粗糙度A 级下的区间范围均有所减小,主要是两辆测试车信号相减的方法只能减少路面粗糙度影响,不能完全消除路面粗糙度信号,而在路面粗糙度等级增大的情况下,偏离真实梁式桥阻尼比后的某假定阻尼比值下的信号含有的路面粗糙度信号也越大,导致按照图6 框架流程识别的第一阶振型不能居中,识别的梁式桥阻尼比区间范围也会缩小,这对于本文梁式桥阻尼比的识别精度是有益的,但同时考虑到粗糙度等级进一步增大,即C 级粗糙度甚至更高时,即使按照真实阻尼比取值,基于图6 框架流程仍无法使识别的第一阶振型不能居中,导致无法识别梁式桥阻尼比.

因此本文仅模拟了A 级及B 级路面粗糙度水平,分析结果表明:本文提出的新方法可以较好地解决以上两级别路面粗糙度对梁式桥阻尼比识别工作的影响.

2.3 噪音影响下的梁式桥阻尼比识别

为探究在噪音干扰下本文新方法的有效性,在车桥耦合动力学模型分析中对车辆响应加速度信号添加白噪声研究抗噪性,以信噪比作为加噪音水平

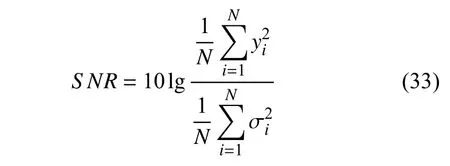
式中,N为数据点个数,yi为第i时刻含有噪声的测试车辆加速度响应,σi为第i时刻的噪声值,SNR为信噪比,单位为dB,其值越大,表示噪音影响越小,信号被干扰程度低,其值越小,表示噪音影响越大,信号被干扰程度越大.

同前,动力学模型真实梁式桥阻尼比为0.01,并考虑B 级路面粗糙度,模拟参数如2.2 节所示基于每个不同噪音水平下的加速度信号按照两辆测试车信号相减后,进行图6 框架流程识别梁式桥阻尼比,如图21～ 图23 所示.

由图21～ 图23 可知:当信噪比大于或等于30 dB 时,梁式桥阻尼比识别效果较好.如图21 所示,信噪比为50 dB 时,当假定阻尼比小于0.009 5时,此时第一阶振型最大值都不处在第一阶振型中点,即会出现左偏现象;当假定阻尼比大于0.010 5时,即会出现右偏现象;而当假定的阻尼比处于0.096～ 0.010 4 时,此时第一阶振型最大值均位于测试跨跨中,可作为识别的梁式桥阻尼比区间,而此时真实阻尼比0.01 恰好也处于该区间范围,识别的阻尼比区间两端与真实阻尼比存在偏差范围4%.而随着信噪比越小,噪音干扰越大,如图22 和图23,识别的梁式桥阻尼比区间范围逐步缩小,识别效果精度进一步提高.以上分析结果表明:本文所提出的新方法进行梁式桥阻尼比识别时,可以较好解决一定噪音程度影响.

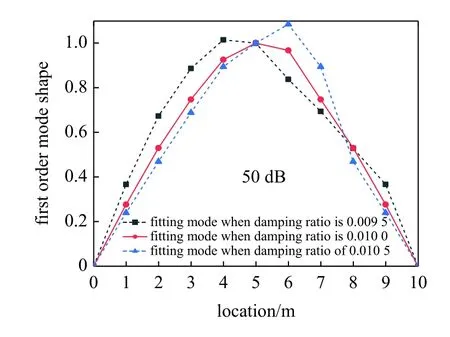
图21 50 dB 下阻尼比识别结果Fig.21 Identification result of damping ratio at 50 dB

图22 40 dB 下阻尼比识别结果Fig.22 Identification result of damping ratio at 40 dB

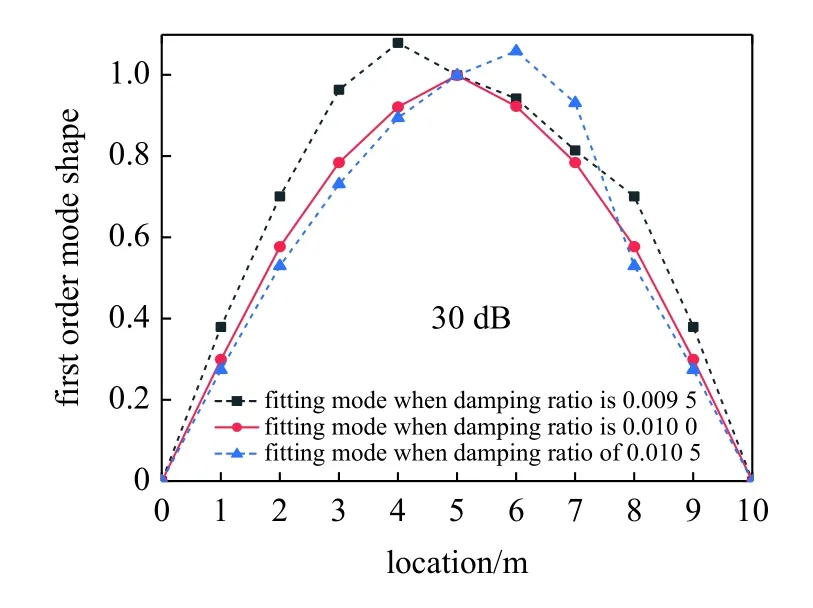
图23 30 dB 下阻尼比识别结果Fig.23 Identification result of damping ratio at 30 dB

3 实桥试验

本次试验中所选取的梁式桥为李子湾桥,如图24 和图25 所示,并选取梁式桥第三跨作为测试跨,该桥位于重庆市涪陵区,该梁式桥属于简支梁桥,梁式桥总长为192 m,宽12 m,双车道,共有六跨加两段引桥组成,即(6+30 × 6+6) m.桥面全宽:0.5 m (栏杆) × 11 m (车行道) × 0.5 m (栏杆)=12 m,上部主梁结构为6 m × 30 m 预应力混凝土空心板,横向由12 片空心板构成,如图26 所示.根据设计图纸及现场几何测量计算得该12 片空心板结合铺装层合成断面的截面惯性矩为0.79 m4,由图纸和检测报告中得到的混凝土强度对比,确定该桥的混凝土弹性模量为32.5 GPa.

图24 李子湾大桥正面照Fig.24 Frontal view photo of Liziwan bridge

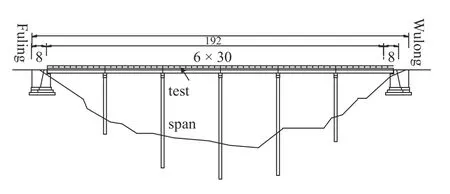
图25 李子湾桥示意图(单位:m)Fig.25 Schematic diagram of Liziwan bridge (unit:m)

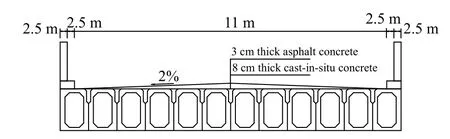
图26 李子湾大桥断面示意图Fig.26 Cross-sectional view of Liziwan bridge

测试车及传感器等如图27 和图28 所示,试验选用的传感器为TST126 磁电式速度传感器,它可以用于测试加速度、速度和位移,其加速度灵敏度为0～ 0.3 m/s2,最大量程20 m/s2,分辨率为3 ×10-6m/s2,频带范围为0.25～100 Hz;牵引车和测试车连接是近似铰接的连接,连接方式如图29 所示,且桥梁较平整,对于测试影响较小;此外,采集信号为微振动下的桥梁,不须考虑轴距滤波效应.试验所采用的数采系统为泰斯特TST5912,它为通用型动态信号测试分析系统.该信号采集系统的采样频率可以设定较大的范围:0.3 Hz～ 100 kHz,准确度高,杂讯少,连接简单.

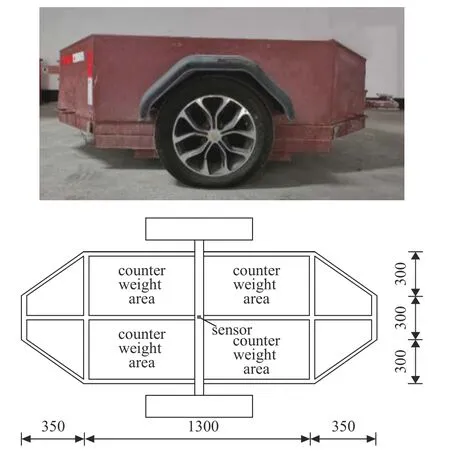
图27 测试车与传感器布置图(单位:mm)Fig.27 Test car and sensor layout (unit:mm)

图28 传感器与数采系统Fig.28 Sensor and data acquisition system

图29 牵引车与检测车连接方式Fig.29 Connection mode between tractor and testing vehicle

为测试此次试验测试车与桥的固有属性,正式试验前的准备试验包括:(1)强迫振动实验,在测试车上施加竖向冲击力,使其在垂直方向发生自由振动,从而获取车辆固有频率;(2)梁式桥微振动试验,基于直接在桥面上放置的加速度传感器获取梁式桥的频率和阻尼等固有特性;(3)传递性实验,基于静止放置于桥上的测试车,利用放置在车体上的传感器获取振动响应,其目的在于验证梁式桥响应是否能良好地传递至车体响应中,进而识别梁式桥的第一阶振型.

其中强迫振动试验频域分析如图30,加载后测试车车体频率均为3 Hz;梁式桥微振动试验,基于两辆测试车车距,选择该桥第三跨为测试跨,图31表明该跨梁式桥的自振频率为3.71 Hz.测试车辆传递性试验频域分析如图32,对应峰值分别代表车频及桥频,可以认为在车体加速度信号中包含车体频率的信息和梁式桥频率的信息,表明梁式桥振动信号能够传递到车体响应中.

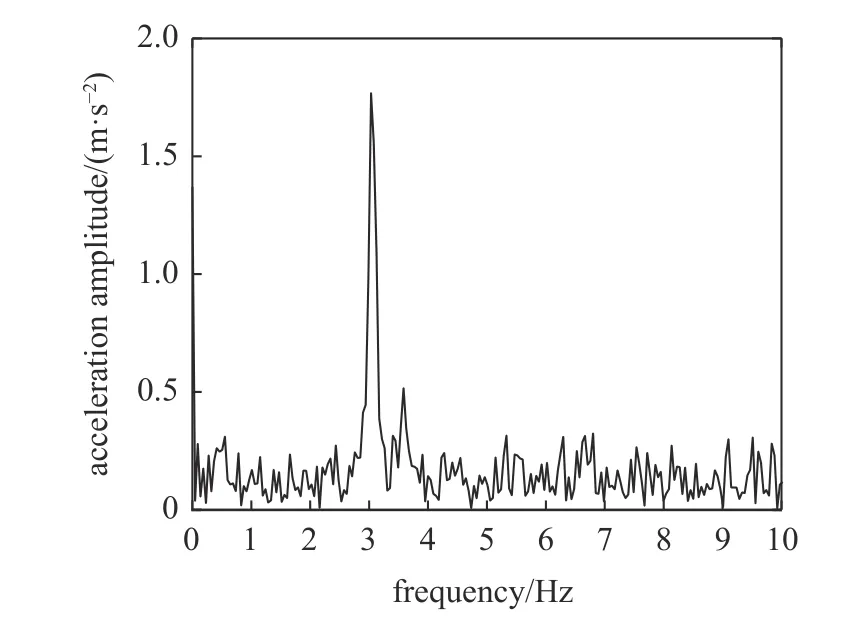
图30 敲击测试车轮轴一侧位置加速度信号频域图Fig.30 Frequency domain diagram of the acceleration signal on the side of the wheel axle for the impact test

图31 桥面1/4 跨处加速度信号频域图Fig.31 Frequency domain diagram of acceleration signal at 1/4 span of bridge deck

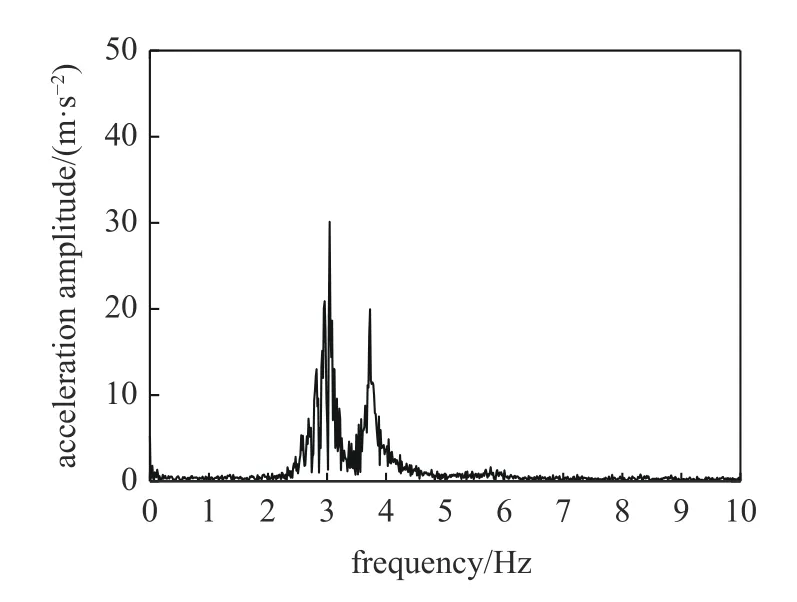
图32 车体加速度信号频域图Fig.32 Frequency domain diagram of vehicle body acceleration signal

由于地处偏远,周围较安静,同时选择无车流量时间段进行试验,可认为环境噪声干扰弱.该梁式桥桥面为沥青混凝土面层,整体路面状况良好.两辆测试车空车重量均为490 kg,通过增加不同块数钢板使大测试车达到1067 kg、小测试车达到1032 kg 的配重,通过随机子空间法计算两辆测试车阻尼比均约为0.023.

此次试验过程为:按上述质量配重进行牵引车拖动大测试车通行梁式桥,并保持两车轮轴间距2.4 m,通行中保持以1 m/s 左右速度运行,采样频率为100 Hz.然后重复上述过程拖动小测试车通行梁式桥.期间时刻关注车体的俯仰、撞击情况,并及时记录通过每跨的时间长度.

基于上述试验过程所获得的时程信号以及识别结果如下图33～图36 所示.

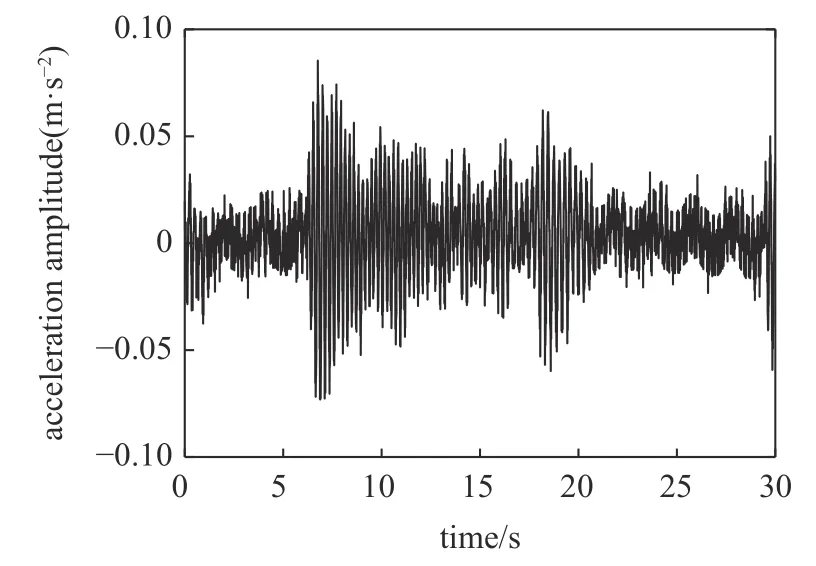
图33 大测试车时程信号Fig.33 Big test vehicle time signal

图35 是基于实测小车信号频域图,从两个峰值可知该测试车信号同时包含测试车频率信息与梁式桥频率信息,这也与上述传递性试验对应.

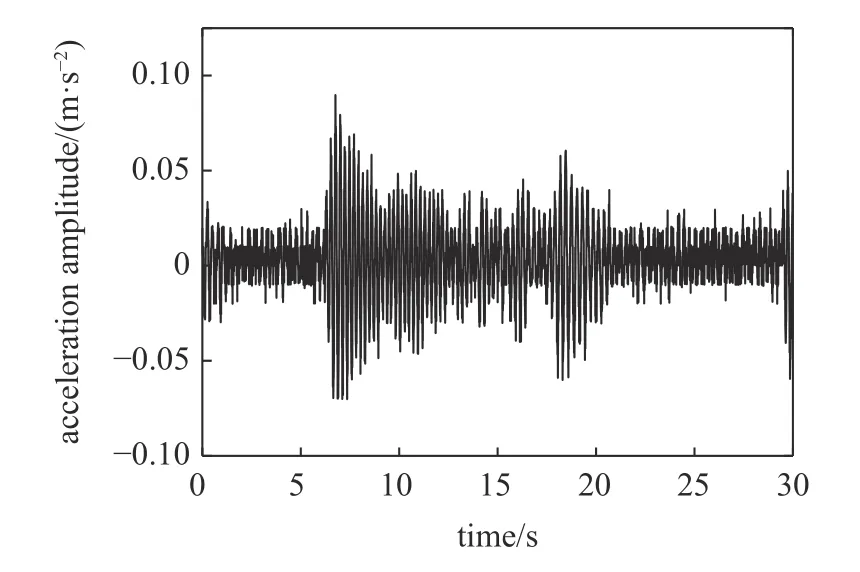
图34 小测试车时程信号Fig.34 Small test vehicle time signal

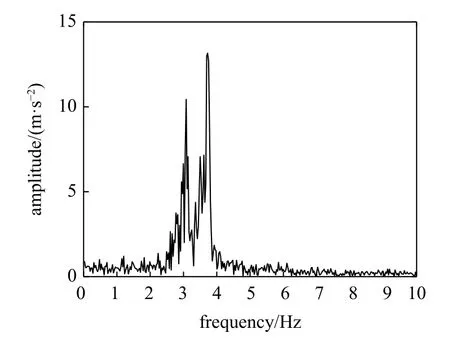
图35 小测试车频域图Fig.35 Frequency domain diagram of small test vehicle

图36 是依据试验所得时程信号按照图6 框架流程的梁式桥阻尼比识别结果:当假定阻尼比为0.007 8 时,第一阶振型位于跨中,且较为对称;当假定阻尼比小于0.007 时,第一阶振型最大值偏左,当假定阻尼比大于0.008 7 时,第一阶振型最大值偏右,而当假定阻尼比处于0.007 0～ 0.008 6 之间时,此时左偏右偏现象均不明显,均可作为识别梁式桥阻尼比在合理区间范围.同时,由表2 所示,通过梁式桥上直接放置传感器采集的测试信号,得到的无车流下的梁式桥阻尼比为0.007 7,采用本文方法识别的阻尼比区间两端与直接测试法得到的阻尼比偏差范围在11%以内,反映了基于车桥耦合动力学理论提出的本文方法具备一定可靠性.

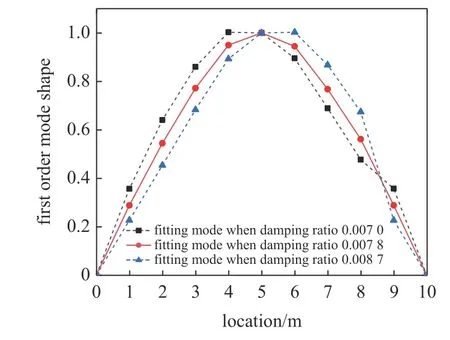
图36 识别结果图Fig.36 Recognition result

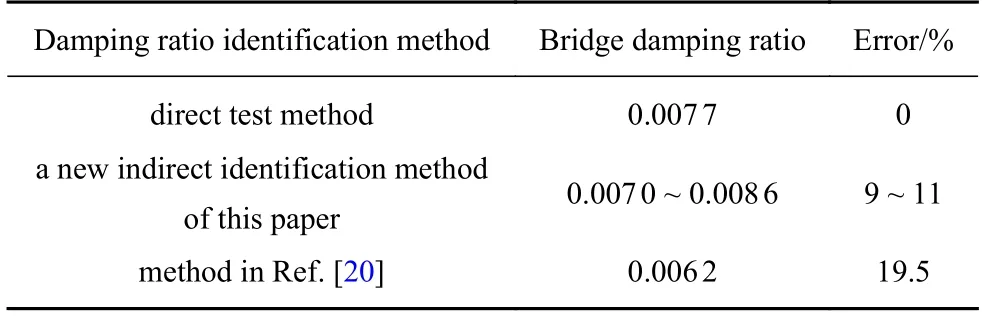
表2 直接测试法与本文及文献[20]方法识别阻尼比值对比表Table 2 Comparison of the direct test method and the method in this paper and Ref.[20] to identify the damping ratio

表2 中列举了传统的直接测试法、本文新方法及文献[20]方法基于本次试验测试数据进行改进后识别的阻尼比值.传统的直接测试法如引言部分所述操作相对繁琐且费时费力,但仍为现阶段主流方法.可认为其识别值为标准值;本文方法在不需要假定参数情况下根据实测加速度信号按照图6 流程调试阻尼值范围为0.007 0～ 0.008 6,误差范围9%～11%;相对简单方便;文献[20]在结合桥梁弹性模量、桥梁质量及惯性矩等假定参数下,基于加速度信号改进后进行多步优化识别的阻尼值为0.006 2,误差范围为19.5%,显著高于本文方法误差且相对繁琐.针对前述文献中提及的其他方法由于其采用的双轴车模型较复杂,且设计需要布置多个传感器测试信号,与本文试验条件相差较远,操作相对困难,所采集数据暂无法应用分析,因此未列入表2 中展示.综合对比表2 可知,本文方法实测精度与直接测试主流方法测试值更接近,但操作相对简单方便,也无需假定设置参数.

4 结论

本文基于有阻尼简支梁式桥与无阻尼简支梁式桥存在的关系理论,以最终识别第一阶振型最大值是否位于跨中作为指标,提出了识别梁式桥阻尼比的新方法,通过车桥耦合动力学模型算例验证了该方法在各类外界影响因素下识别梁式桥阻尼比的可行性,并通过实桥试验数据进行初步分析,得出以下结论.

(1)采用本文新型阻尼比识别方法能一定程度上克服影响梁式桥阻尼比识别效果的桥面粗糙度、环境噪音等因素影响.

(2)车桥耦合动力学模型分析表明,本文所提出的方法适用于测试车低速运行在1 m/s 左右,梁式桥阻尼比不大于0.02,路面粗糙度A 和B 级以及信噪比不低于30 dB 的情况.

(3)与其他间接技术识别梁式桥阻尼比相比,本文方法具有设置参数少、操作简单方便以及具有更高测试精度等优势,且本方法后续将进一步开展随机车流影响及其他梁式桥类型研究,进一步推动基于车桥耦合动力学理论识别梁式桥模态参数的实际工程应用.