柔性轮对的离散时间传递矩阵法建模及垂向振动1)

刘鹏飞 *, 杨绍普 *, 刘永强 ** 顾晓辉 *, 刘泽潮 *,

* (石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043)

† (石家庄铁道大学河北省交通工程结构力学行为演变与控制重点实验室,石家庄 050043)

** (石家庄铁道大学机械工程学院,石家庄 050043)

引言

轮对是轨道交通车辆最为重要的走行部件,发挥着承载、牵引、制动及导向等重要功能,但同时属于簧下质量,在长期使用过程中,车轮踏面及轨面不可避免会出现剥离掉块、擦伤、波磨及车轮多边形等典型的短波不平顺激扰,容易激发轮对的中高频结构振动,甚至轮对结构与轨道结构的自振频率相吻合而演化为系统的耦合共振,由此恶化了列车的运行环境并加剧轮轨缺陷的进一步发展.因此在车辆系统中,中高频域动力学研究中考虑轮对结构振动十分必要,对于延缓和消除相关问题的产生具有重要意义.

近年来,从轮对柔性建模及动态仿真问题,国内外相关学者开展了大量研究.主要的研究方法是,基于有限元软件进行轮对弹性建模,提取振动模态,之后与动力学软件进行联合仿真,进而实现非线性振动的求解.例如,文献[1-12]主要建立了轮对的有限元模型,进一步与动力学仿真软件结合,从而开展中高频轮对合理建模问题[1]、轮轨磨耗问题[2]、多边形激扰问题[3-4]、车轮扁疤冲击振动问题[5-6]、车辆运动稳定性问题[7]、钢轨波磨激扰问题[8-9]、轴承寿命问题[10]、滚动噪声问题[11]、轮轨摩擦自激振动与轮对弯曲振动耦合问题[12]等方面的研究.可以看出,相关的建模方法和仿真技术也是当前刚柔耦合动力学的主要研究手段.此外,国内外学者也在积极探索轮对弹性振动建模的其他方法.如Guiral 等[13]在非惯性车辆运动参照系的框架内推导出了一种柔性轮对的计算公式.Baeza 等[14]给出了三种基于欧拉方法的柔性转动固体动力响应计算公式,适用于固体与非旋转结构相互作用的研究.徐宁等[15]利用假设模态法,得到带有集中质量及转动惯量的弹性车轴振型函数,从而建立考虑轮对弹性振型的车轴模型.文献[16]利用欧拉坐标系中的拉格朗日方程和模态叠加法,建立和求解轮对弹性振动的运动方程.崔潇等[17]采用欧拉坐标系下旋转效应柔性轮对模型进行刚柔耦合车辆-轨道系统多体动力学建模,杨云帆等[18]采用欧拉梁模拟轮轴弹性振动,建立了考虑轮对柔性的直线电机地铁车辆动力学模型.

总体而言,轮对弹性振动的建模方法较为成熟,有限元方法最为常用,通过模态叠加原理实现随机激扰下轮对结构振动与车辆振动的求解,结合有限元和动力学软件是一种有效的途径.但无论是基于有限元法还是直接推导轮对的弹性振动方程,结构改变后往往需重新建模和推导,较难实现模块化,计算机编程也略为复杂.近年来,传递矩阵法已突破线性振动的限制,通过时间离散实现了转子系统、武器系统等非线性动力学及弹性振动问题的求解[19-22],该方法通过可将振动系统分解为一定数量的离散单元,各单元均可独立编制传递矩阵,最后再通过单元边界处的力和运动状态向量集成为整体振动系统,无需推导系统总体动力学方程,因而具有求解规模少、模块化组合、易于编程等优点,但相关方法在轨道交通车辆动力学研究中还鲜有报道.

因此,本文以机车车辆单轴滚振试验台为研究对象,引入分布质量弹性轮轴的离散时间传递矩阵、车轮传递矩阵等,进一步建立考虑轮对弹性振动的试验台刚柔耦合动力学分析模型,综合新型显式积分法、Newmark 隐式积分法和Riccati 法对系统振动进行数值求解,最后通过单轴滚振试验台的测试结果对仿真模型进行验证,以期为考虑结构部件弹性振动的车辆-轨道耦合系统动力学研究提供新的建模方法和研究思路.

1 分布质量弹性轮轴离散时间传递矩阵

用传递矩阵法对轮对建模时,可将轮对分为分布质量弹性轮轴和集总质量的车轮等刚体部件,通过状态向量与传递矩阵的关系实现截面力和运动量的传递计算.状态向量用于描述部件端部的剪力、弯矩、位移及加速度等力和运动量.文献[19]中系统建立了以力、位移为状态变量的传递矩阵法.文献[21]针对无质量弹性梁-滑动轴承-圆盘系统进行了研究,同时指出,研究轴系结构瞬态响应时,由于弹性模量大、时间步长小,可能出现病态矩阵,采用力、加速度的状态向量可尽力避免此问题.鉴于此,首先设定轮轴状态变量W为

式中,M为截面力矩,Q为剪力,为截面转角加速度,为截面的垂向振动加速度.

建立分布质量弹性轮轴离散时间传递矩阵的本质在于确定弹性轴输入端和输出端状态向量的力学传递关系.对于动力轮对结构(图1),从参振的角度可大体分为轴箱、车轮、齿轮箱与轮轴四个部分,其中轮轴作为相对的细长结构,贡献了主要的弹性振动能量.弹性轮轴可视为弹性梁结构,假设其第i段长度为li,梁的线密度为ρ,在车辆坐标系中定义左侧为输入端,剪力QL,弯矩ML,定义右侧为输出端剪力QR、弯矩MR,则其受力状态如图2 所示,对应的左右侧位移为ZL和ZR,g为重力加速度,ρg为梁上分布质量的重力分布.

图1 轮对结构Fig.1 Wheelset structure

图2 分布质量弹性轴的受力与变形Fig.2 Force and deformation of elastic axle with distributing mass

设梁的弹性振动位移用模态叠加法求解,引入正则振型函数φ(x),正则振型坐标q(t),则梁在距其左端面x处、t时刻的弹性位移可表示为

根据其剪力和弯矩平衡关系,并考虑惯性力,可建立梁单元的受力平衡方程式(3)和式(4),对于输入端到输出端的垂向位移及转角变形,同样根据剪力、弯矩及分布载荷条件下的梁弹性变形进行叠加可得到变形方程式(5)和式(6)[22]

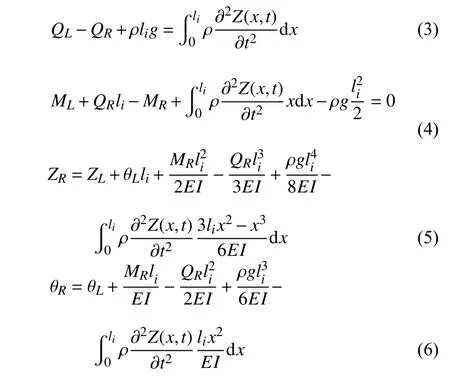
式中,EI为梁的抗弯刚度.式(3)～ 式(6)即为输入端到输出端的分布质量弹性梁的力和位移传递关系.为了进行数值积分求解同时保证弹性梁振动求解的收敛性和稳定性,引入Newmark-β隐式积分法进行上述四式的改造[19].Newmark-β法积分格式如下

基于式(7)～ 式(10),将式(3)～ 式(6)中的位移项表示为当前时刻加速度及上一时刻加速度、位移及振动速度的显式表达,则改造后的位移公式可进一步表达为式(11)和式(12)

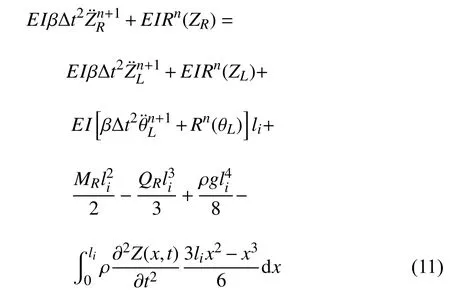
上式中还存在积分项,进行传递矩阵推导的关键在于消除模态函数积分项中的正则加速度坐标.以式(3)中积分项为例,若取前4 阶模态,结合式(2),可知

根据振动力学,梁端位移和转角的加速度满足如下关系

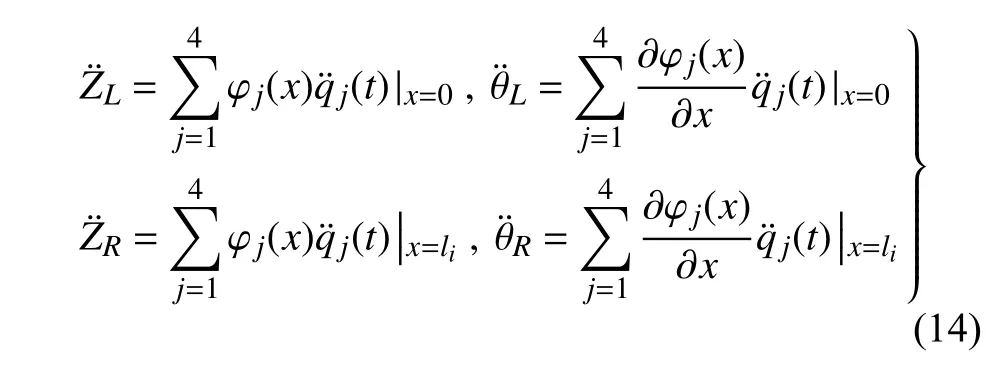
于是可将转角、位移的加速度统一用矩阵表示为式(15),式中U为可用模态函数求解出的系数矩阵

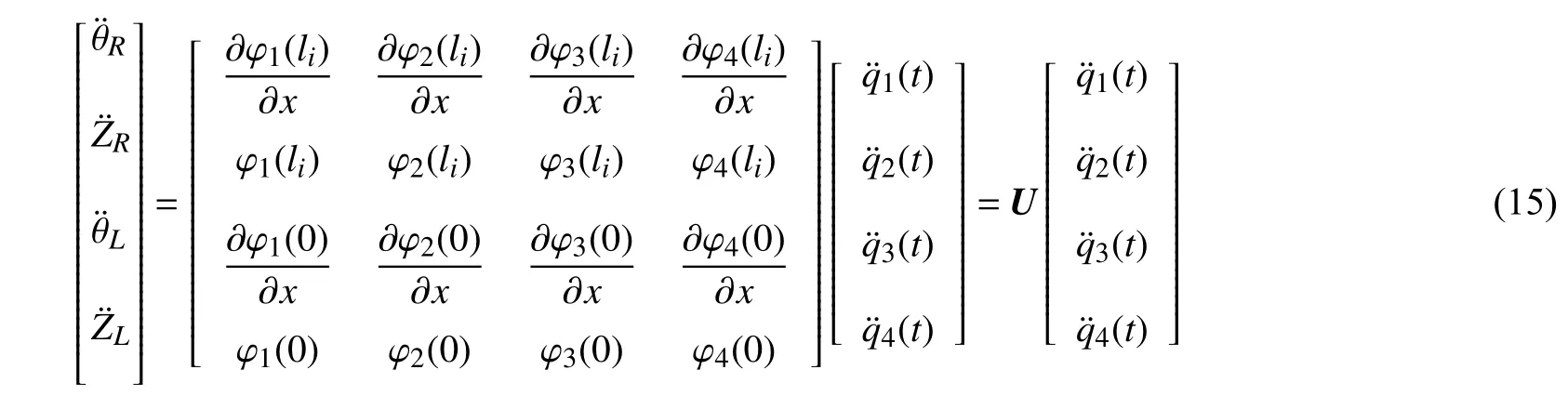
令

则关于振型函数的定积分项可表示为

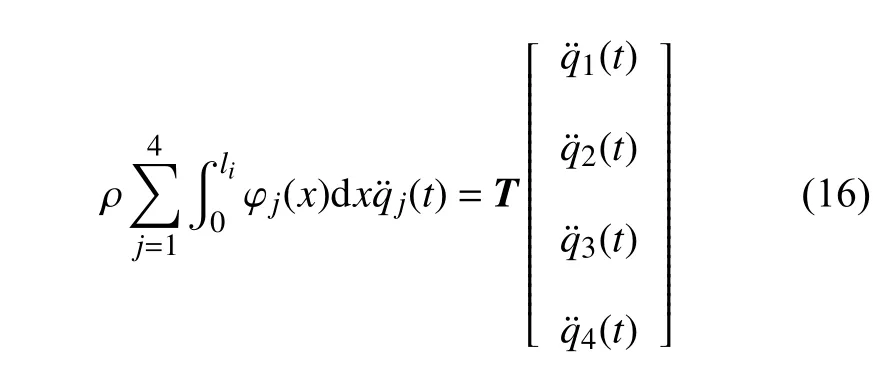
对比式(15)和式(16),加速度状态向量与积分项的矩阵表达都是关于正则坐标加速度的.那么,如果通过加速度状态向量的线性叠加组合来表示该积分项,就可消除原方程积分项中关于时间的正则振型坐标加速度.为此,引入待定系数a1～a4,则积分项可进一步表达为

式中,左端和右端项可约掉正则振型坐标加速度项,左右侧再经过转置,可得

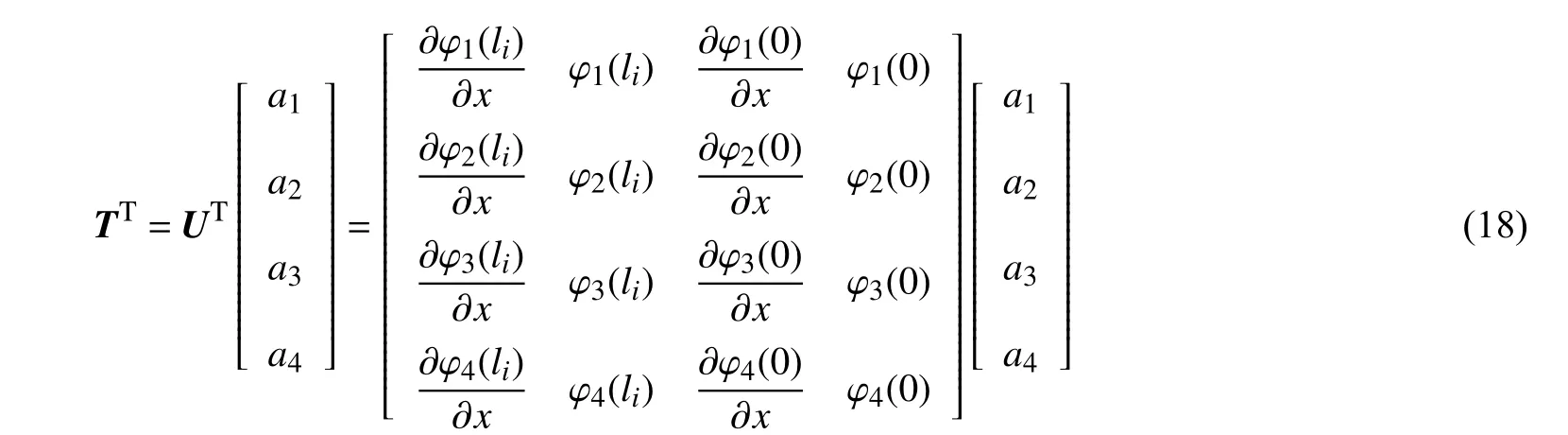
最终通过矩阵运算,可得待定系数a1～a4的具体数值

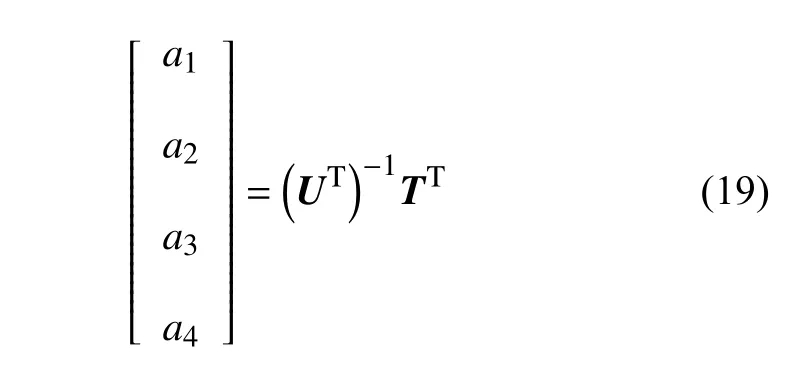
式(18)中,方程的左侧是正则振型函数关于轴长度的积分,在已知振型函数后,可直接求得结果,同样转置矩阵UT也可通过振型函数获得,于是关于待定系数a1～a4的求解就转化成了一阶常系数线性方程组的求解问题.只要振型假设合理,矩阵UT可逆,便可求出待定系数的具体量值,也即表明通过轴左、右端的状态向量间接表达了积分项.对于式(18)也可通过高斯消元法快速求解.

同理,对于式(4)、式(11)和式(12)中的包含振型函数的积分项,采用类似方法也可得到对应的组合待定系数bi,ci和di(i=1～ 4).最终,将方程式(3)～式(4)、式(11)～式(12),统一表达为如下矩阵形式

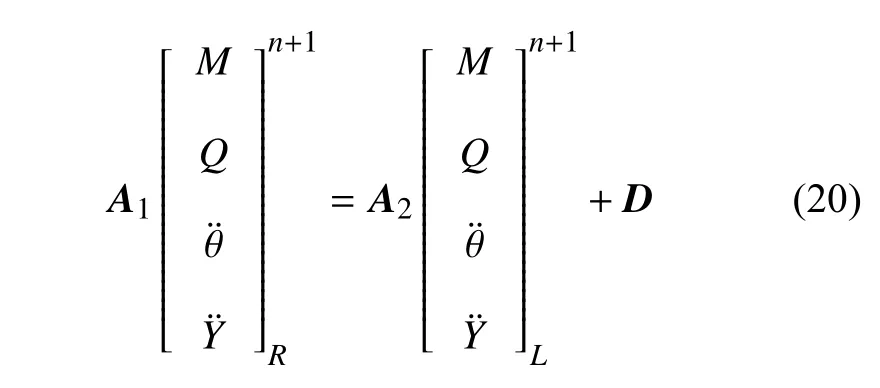
则,左右端的传递关系可转变为

式中,H和D′矩阵为轴段的场传递矩阵,A1和A2及D为推导出的中间矩阵,且满足下式

2 车轮、齿轮箱及弹簧阻尼系统传递矩阵

对于车轮,简化为具有垂向、侧滚位移的刚体处理,其左、右侧受力状态及状态向量如图3 所示.刚体质心两侧的转角、位移均相同,基于达朗贝尔原理,根据垂向力平衡和转矩平衡关系,不难推导出其振动微分方程,此处不再赘述,直接给出车轮的传递矩阵,如式(25)中Hw和Pw.

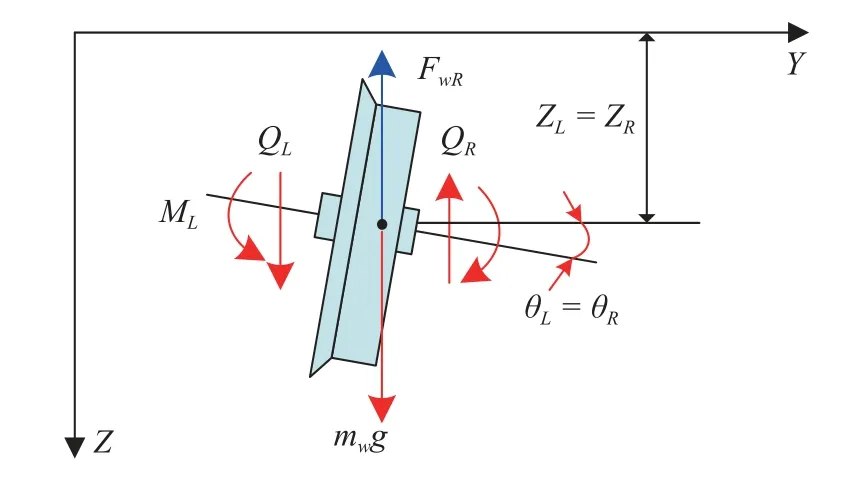
图3 车轮受力状态Fig.3 Force conditions of wheel

式中,Jw为车轮侧滚惯量,mw为车轮质量,Fw为轮轨垂向力,Mw为侧滚蠕滑力矩.

对于齿轮箱,将其2/3 质量作为簧下参振质量,与弹性轮轴连接,则式(25)中传递矩阵同样适用于齿轮箱.对于轴箱,仅考虑轴箱的垂向振动,为此式(25)中进一步令Jw和Mw=0 即可.

转向架系统中,轴承、一系和二系悬挂均可一定程度上简化为刚度-阻尼力元,本文以轴承为例进行说明.如图4 所示的弹簧、阻尼系统,弹簧刚度为Kb,阻尼系数Cb,左右侧的位移不相等,剪力相同、方向相反,若不考虑该系统的弯曲刚度和阻尼,可认为左右侧的弯矩相同,则满足式(26)中的数学关系

图4 弹簧-阻尼系统受力状态Fig.4 Force conditions of spring-damping system

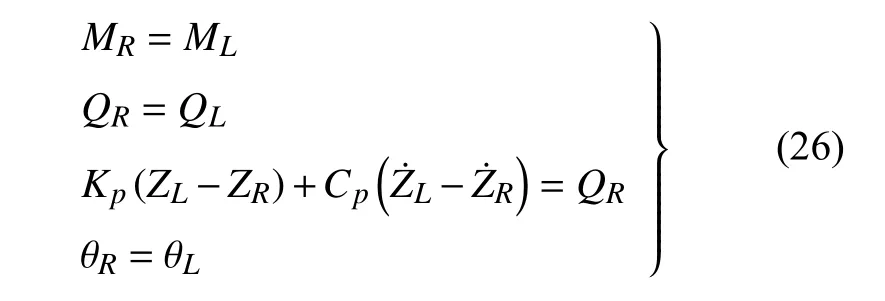
进一步,将式(26)采用矩阵表示,并引入Newmark-β法积分格式对其改造,最终可得到式(27)的表达形式,即为该力元的离散时间传递矩阵

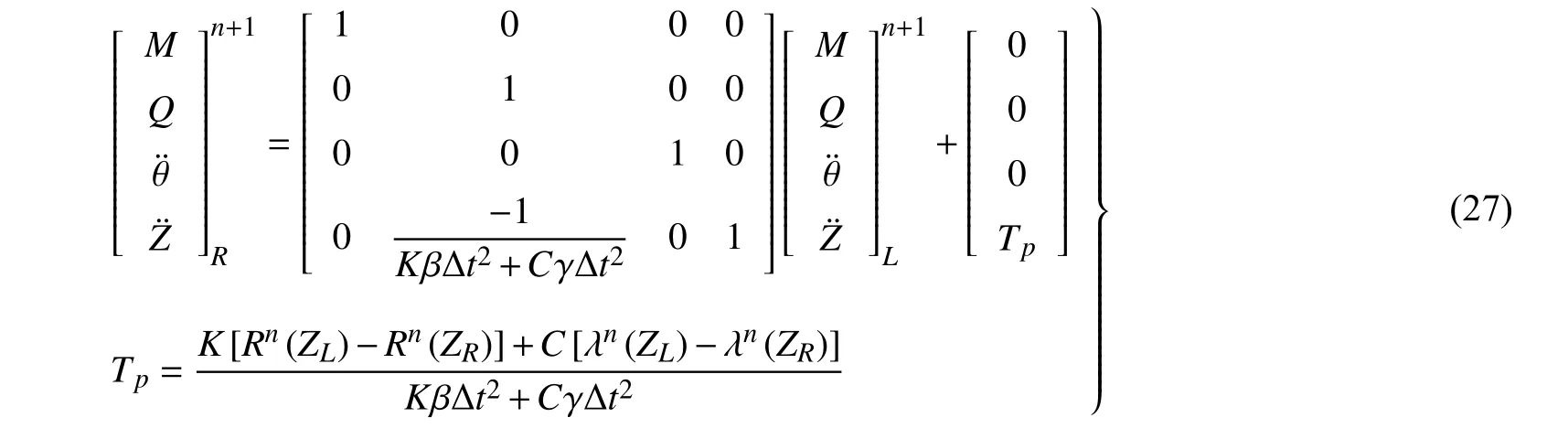
3 单轴滚振试验台的垂向动力学建模及求解方法

3.1 动力学建模

以单轴滚振试验台为例(图5),建立其动力学模型(图6).需要指出的是,模型分为两部分,一为轮对系统,基于上文的离散时间传递矩阵法进行建模;二为虚拟构架和轨道轮组部分,直接给出动力学方程,并采用新型显式积分法(翟方法)[23]求解其速度和位移响应.这样处理的目的是,轮对之外的系统采用显式积分法求解容易编程实现,且无需联立求解高阶代数方程组,可进一步提高计算效率.建模时,可将轮对弹性体作为子模型,方便后期与车辆-轨道耦合动力学模型、列车-轨道动力学模型[23-26]及其求解方法进行对接,同时也可通过本次分析和试验,来检验复杂刚柔耦合系统中显、隐式混合积分求解振动的可行性.

图5 单轴滚振试验台系统构成Fig.5 Compositions of single-wheelset rolling and vibration test system

轮对发挥弹性振动的主要结构是轮轴,可将轮轴采用分布质量弹性梁建模.轴承的支撑刚性和阻尼则简化为弹簧-阻尼力元.如图6 所示,本文将轮对-齿轮箱系统从左到右分为12 个部分,3,5,6,8,10 为弹性轴段,采用式(21) 中传递矩阵;轴箱体1 和12 采用式(25)传递矩阵,但仅考虑垂向振动;轴承力元2 和11 采用式(27)中的传递矩阵;车轮4 和9 及齿轮箱7 采用式(25)的传递矩阵.

图6 试验台动力学模型Fig.6 Dynamic model of test rig

对于刚性构架和轨道轮,仅考虑其垂向运动,对应的振动微分方程为

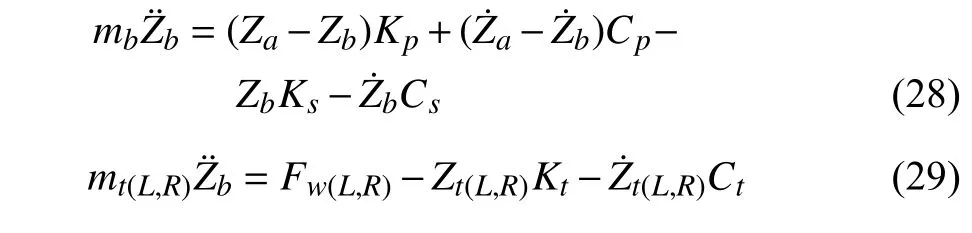
由于针对垂向振动,轮轨垂向力简化为Hertz 非线性接触弹簧[23],以右轮为例,作用力可表示为

式中,R为车轮名义滚动半径,Z0(t)为t时刻轨道不平顺,ZtR(t)为轨道轮垂向位移.诚然,轮-轮接触和轮-轨接触有一定差异,若考虑空间接触关系,需进一步描述轮-轮接触斑形状、蠕滑力的不同,具体可参考文献[27].

3.2 振动求解方法

下面重点阐述基于Riccati 法来求解轮对系统的振动加速度.基于离散时间传递矩阵法建立的各部件传递矩阵均具有如式(31) 的统一形式,其中,H11,H12,H21,H22为2 × 2 阶方阵,F,E为2 × 1阶列阵.将状态变量W分为力状态变量和加速度状态变量两部分,分别对应f和,如式(32)所示

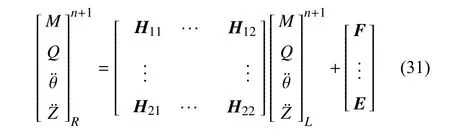
引入Riccati 变换[21,23],第i截面端部力f和加速度状态变量之间满足如下关系

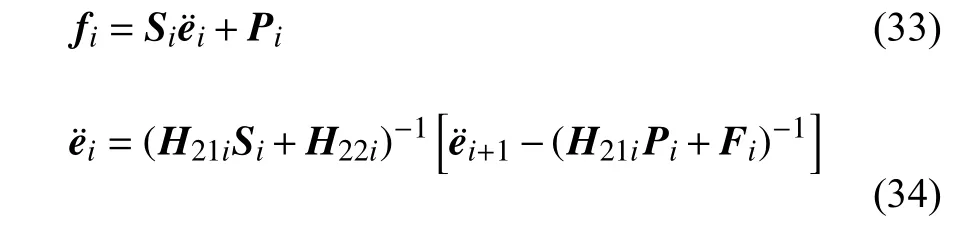
式中,各单元对应的Pi和Si矩阵可由下式递推计算

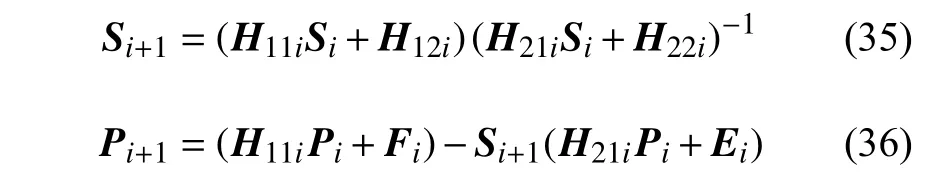
依据系统的边界条件确定式(33)～ 式(36)的边界状态.对于左侧轴箱,边界条件满足f=0,=0,那么可知P0=0 且S0=0,由式(35)和式(36)依次递推出各截面的P和S矩阵.进而,由最右端满足f13=0,=0,则通过下式(37)确定最右端的加速度矢量.最后根据式(33)和式(34)依次获得各截面的加速度和力状态变量

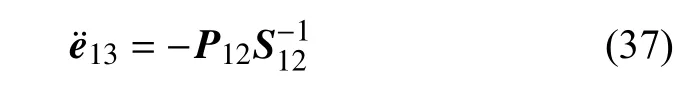
本文模型的求解涉及了3 种重要的计算方法,系统总体求解流程如图7 所示.具体的求解步骤为:

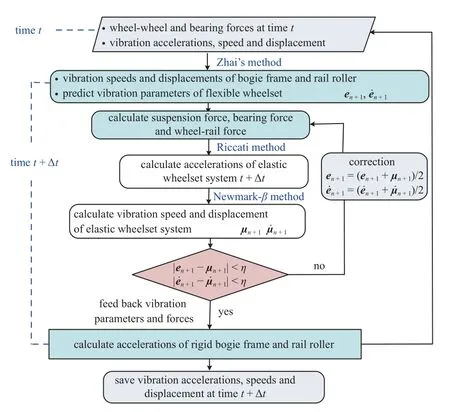
图7 动力学模型数值求解流程Fig.7 Numerical solving flow of dynamic model

(1) 获取t时刻的振动位移、速度,以及轮轨力、轴承力等线性及非线性作用力;

(2)采用新型显式积分法(翟方法)计算刚性构架、轨道轮t+Δt时刻的位移和速度响应,预估柔性轮对系统振动位移和速度;

(3)基于第(1)步结果和第(2)步预估结果,计算t+Δt时刻一系悬挂力、轮轨力、轴承力;

(4)采用Riccati 方法计算柔性轮对系统振动加速度;

(5) Newmark-β法计算t+Δt时刻柔性轮对系统的振动速度、位移;

(6)检验第(2)步预估振动量和Newmark-β法积分求解振动量的差异是否小于允许误差,若大于设定误差,进行预估振动量与积分振动量的平均,再返回步骤(3),重新计算悬挂力、轮轨力;重复上述步骤,直到误差低于设定阈值,即获得需要的轮轴系统振动速度、位移;

(7)反馈轮对系统振动量及一系悬挂力、轮轨力至构架、轨道轮组成的外部系统,通过振动方程直接计算下一时刻构架、轨道轮的加速度;

(8)保存t+Δt时刻系统的位移、速度和加速度,作为下一时刻积分的初始条件.

4 轮对振动特性数值仿真和试验验证

针对单轴滚振试验台及轮对进行数值仿真和同步试验.基于假设模态法,文献[22]确定振型函数,并代入到前文分布质量弹性轴的传递矩阵中.建模涉及的主要参数在表1 中列出,其中轴承的刚度和阻尼可参考文献[28]的计算结果,轨道轮组下部其支承刚度和阻尼参考文献[29].至于柔性轮对的自振特性,可直接参照文献[30]中作者前期给出的计算方法,采用传递矩阵亦可方便求解,对于本文所研究的动力轮对,其所考虑的最高阶模态为3 阶弯曲模态,对应频率为560 Hz.

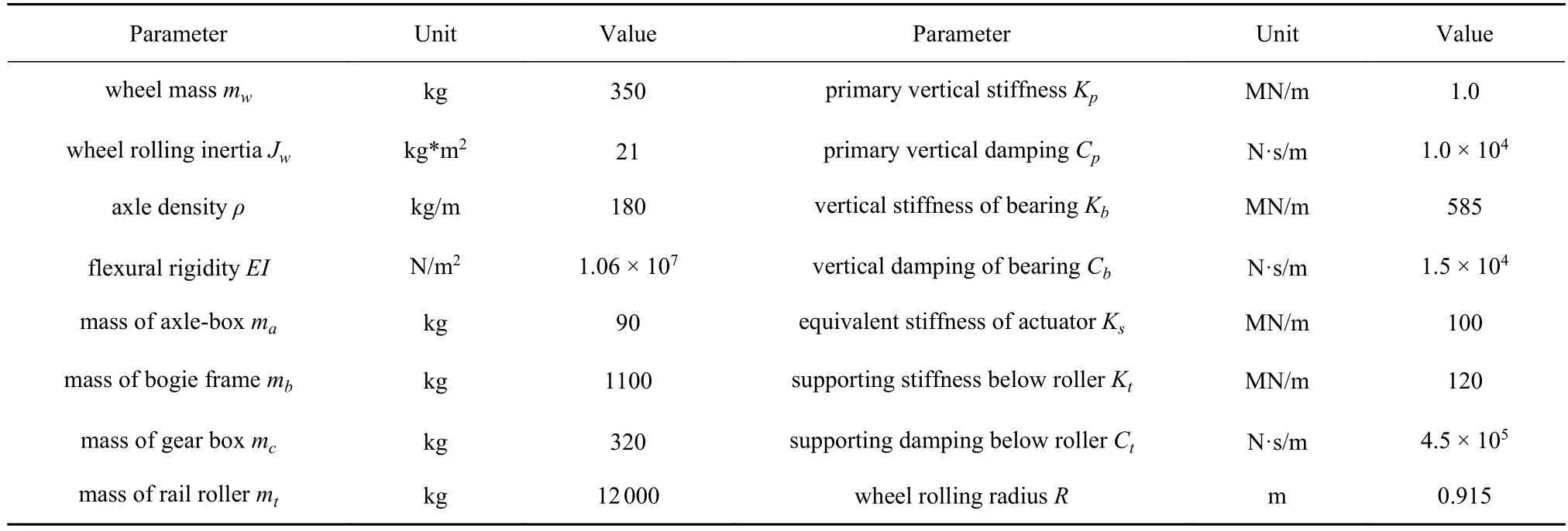
表1 主要建模参数Table 1 Main modeling parameters

4.1 轨道轮切削、打磨与测试

为了检验理论模型的正确性,开展了300～400 km/h 速度级轮对激振试验,轨道轮直径1.8 m,车轮名义滚动直径0.915 m.对车轮和轨道轮进行了表面几何状态测试(图9),并对轨道轮进行了多边形打磨.测试结果显示(图10),轮对有初始的一阶不圆顺,轨道轮即使通过切削加工也存在较低水平的粗糙度,但幅值不超过0.03 mm.进一步通过局部打磨模拟了轨道轮多边形和局部凹陷.其中多边形的波长157 mm,对应于轨道轮36 阶多边形,幅值不超过0.05 mm,局部凹陷波长300 mm、波深0.3 mm,代表单一的谐波不平顺,轨道轮切削后初始的轨面粗糙度水平较低.在试验中,车轮不圆顺始终参与系统激振,为此在仿真中将车轮多边形作周期延拓,并与轨道轮3 种激扰进行叠加,形成复合不平顺(图10(c)),以此作为仿真模型的轮轨接触界面输入激励.

图9 室内试验Fig.9 Laboratory test

图9 室内试验(续)Fig.9 Laboratory test (continued)

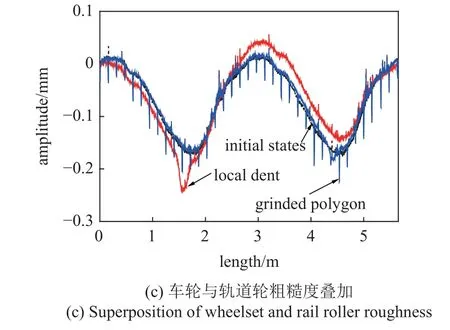
图10 轮对及轨道轮表面几何状态Fig.10 Geometric states of wheelset and rail roller surfaces

4.2 振动特性的试验验证

基于前述离散传递矩阵法建立的弹性轴单轮对动力学模型,进行了理论模型的试验验证,试验过程中,测试了不同轨面状态下的轴箱振动加速度,信号采集采用压电式加速度传感器,采样频率不低于5000 Hz,以尽量涵盖主要的中高频振动.图11 给出了初始不平顺状态下,轮对以400 km/h 速度运行时轴箱加速度测试结果和仿真结果的比较.从频域上看,仿真结果较好捕捉了轴箱1600 Hz 范围内的振动主频峰值,但主要振动能量集中于500 Hz 以内.在时域中,对测试结果进行1600 Hz 和500 Hz 低通滤波,与计算结果进行比较.500 Hz 低通滤波后,测试加速度和仿真加速度幅值总体分别分布在(-3.4～+2.8)g和(-3.6～+3.1)g的范围内,最大幅值相差0.3g左右,约9%.

图11 初始粗糙度状态下仿真和测试加速度比较Fig.11 Comparisons between simulation and test acceleration under initial roughness

进一步,对多边形激扰下的轴箱振动响应进行对比验证,测试和仿真加速度对比如图12 所示,轮对运行速度400 km/h.同样,在频域上看,仿真结果较好反映了实际系统在1510 Hz 范围内主要振动特征,振动主频包含了轮对转频(39 Hz)、多边形激扰频率(707 Hz)及其倍频等.在时域响应上,对测试结果进行1510 Hz 和1000 Hz 的低通滤波,幅值分布在 ± 8.5g和-6g～ +7.5g的范围内,仿真加速度幅值总体在-6g～ +7.9g的范围内,因此在1000 Hz 频率内,测试和计算结果幅值相差0.4g,约5%.事实上,在500～ 1000 Hz 的频率范围内,仅轨道轮多边形激扰引起的强迫振动较为显著,其余频率对应振动能量十分微弱.

图12 多边形激扰下仿真和测试加速度比较Fig.12 Comparisons between simulation and test accelerations under polygon excitation

最后,以轨道轮局部凹陷为主要激励,对仿真模型的计算结果进行了对比验证,由于局部凹陷的幅值较大,考虑运行安全,在试验中将轮对走行速度设定在了300 km/h.同时为研究刚、柔建模方法对系统动态响应带来的影响,也分析了刚性轮对的振动响应,在时域-频域对仿真和实测轴箱振动加速度进行了比较,如图13 所示.对于柔性轮对,仿真结果反映了实际系统在1580 Hz 范围内主要振动特征,但在500 Hz～ 1580 Hz 的高频区段,振动幅值较小,振动能量总体集中于500 Hz 以内.经过1580 Hz 和500 Hz 的低通滤波后,在时域响应上,测试和和仿真结果能清晰识别和捕捉局部凹陷产生的振动激扰成分,加速度幅值范围均在(-19～+21)g之间,响应规律较接近,最大幅值相差在1g之内,误差在5%左右.对于刚性轮对,总体能够反映250 Hz 以内的振动,但超过该频率的高频部分未能充分体现,相较测试结果和柔性轮对计算结果要小,最终在时域响应上,刚性轮对建模的振动加速度幅值分布在 ± 11g范围内,约为实测结果的60%左右,因此基于离散时间传递矩阵法的柔性轮对模型具有更高的求解精度.也进一步表明,采用柔性轮对建模方法能够更好的描述结构在中高频域的弹性振动.

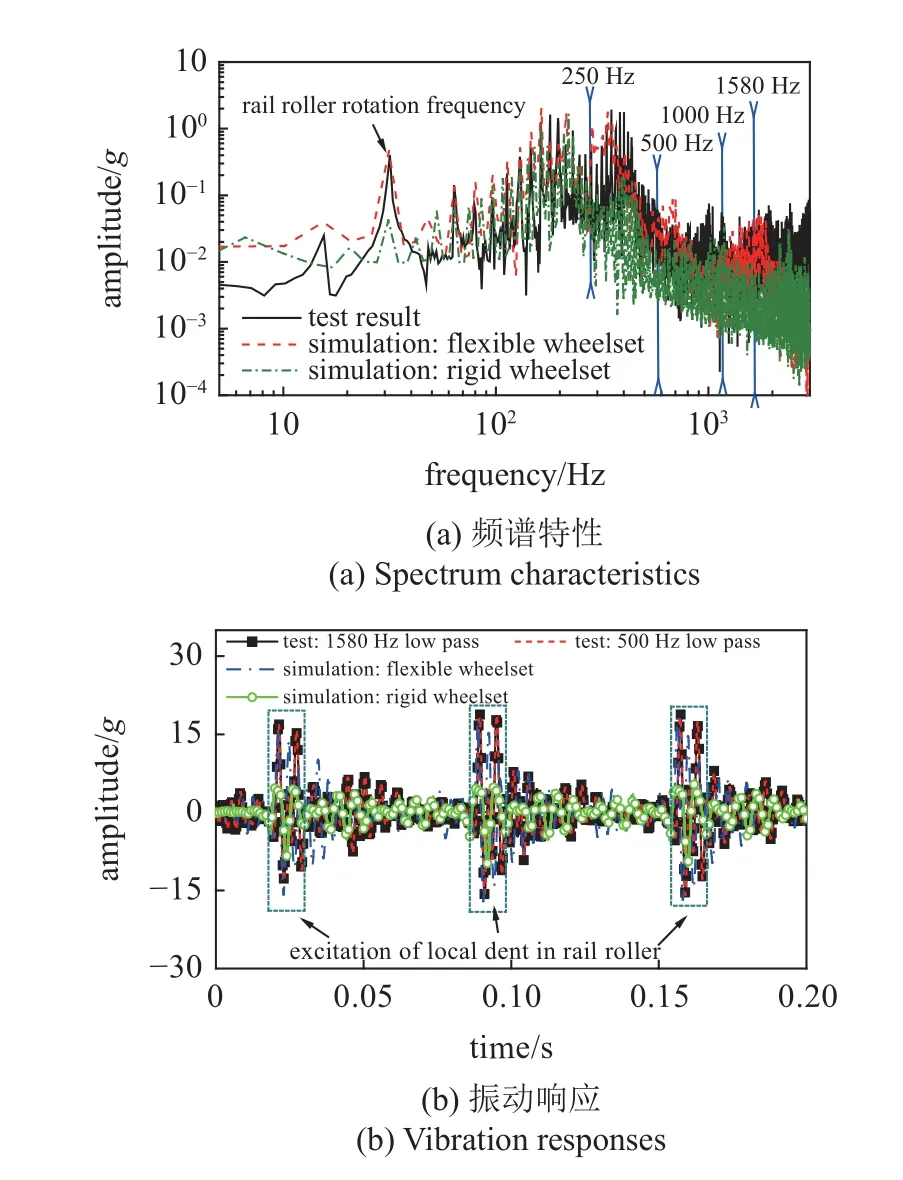
图13 局部凹陷激扰下仿真和测试加速度比较Fig.13 Comparisons between simulation and test accelerations under local-dent excitation

综上所述,基于离散时间传递矩阵法建立的单轮对弹性体模型能够较好模拟轮轨高频激振条件下的振动性能,与单轴滚振试验台的测试结果对比表明,模型在500 Hz 频率范围内的振动能量集中区总体具有较好的适应性.采用新型显式积分法、Newmark-β隐式法对系统的混合积分数值求解方案也是可行的,获得了较好的求解精度.就车轮多边形磨耗而言,根据以往研究,轮对的弯曲振动是其重要诱因之一[31],所建立的理论模型能够反映这一要素.但仍需要指出的是,轮对同时存在扭转、弯曲耦合振动,轮轨法向接触非线性、蠕滑非线性特性同时会影响轮对的结构振动.诚然,在本文研究的工况下以垂向振动为主,后期在车辆-轨道耦合动力学模型进一步集成该模型时,需要综合考虑轮对系统的空间弹性振动形态.另外,离散时间传递矩阵法可实现轴、盘类等形状规则零件的模块化建模,但如何利用该方法对车轮、齿轮箱等空间复杂曲面及结构等高维问题进行动力学建模仍需深入探索.

5 结论

本文以机车车辆单轴滚振试验台为研究对象,推导了弹性轮轴及主要参振部件的离散时间传递矩阵,同时考虑上部构架和下部轨道轮组的振动,建立了试验台动力学分析模型,综合新型显式积分法、Newmark-β隐式积分法及Riccati 方法对系统进行了数值求解.通过打磨轨道轮,开展了高速条件下的轮对运行试验和仿真测试,主要结论如下.

(1)综合对比轨道轮微幅不平顺、多边形冲击和凹陷式谐波激扰下的计算和试验结果,理论模型总体能够捕捉及反映轮对结构中高频的振动特性,特别是在500 Hz 以内的振动能力集中区,时域上的仿真结果响应规律和测试结果比较接近,三种工况下计算的加速度幅值误差分别低于9%,5%和5%.

(2)轮对弹性系统采用离散时间传递矩阵法建模,采用Riccati 方法和Newmark-β隐式积分法求解,外部构架及轨道轮振动则采用显式积分求解,上述混合建模和混合积分求解的思路是可行的.

(3)离散时间传递矩阵方法建模时无需推导系统总体动力学方程,只要具备了各组成部件的传递矩阵,不同模型可调用相应模块并组装即可,且涉及的矩阵阶次低,可实现快速建模及求解.