对比手法在MATLAB教学改革中的应用
王凤,郝向英
(武汉工程大学 光电信息与能源工程学院,湖北 武汉)
Matlab是一款应用十分广泛的数学分析软件[1]。Matlab以矩阵作为数据操作的基本形式,并且还提供了很多数值计算函数,使得运算变得非常简洁、方便。Matlab也提供了很多绘图命令,不仅可以绘制各种图形,还可以对图形进行修饰处理[2]。此外,Matlab还具有强大的符号计算功能、程序语言设计功能和工具箱的扩展功能。在很多高等学校,Matlab成为线性代数、自动控制理论、数字信号处理、动态系统仿真、图像处理等诸多课程的基本教学工具[3-5]。Matlab也是很多科学研究工作者进行理论数值模拟,实验数据分析的首选工具。熟练掌握Matlab语言特点和命令操作是学好Matlab的关键。由于Matlab基础语言较为简单,以往,对该部分的讲解侧重于命令的使用方法,并且花费很少的课程时间去讲解该部分。这种教学模式会使学生感到枯燥无味,并且无法理解每条命令的真正含义,从而导致学生学习兴趣和专注力的降低[6-7]。
对比手法是文学创作中常用的一种表现手法,可以将两种对应的事物对照比较,使形象更鲜明,感受更强烈。对比手法已经应用于一些文学类教学中[8-9],并取得了较好的课堂效果。将对比手法应用于Matlab教学中,在对一些命令讲解时,除了讲解该命令的使用规则,还对比讲解该命令在数学上的求解过程,不仅使学生理解每条命令的具体含义,还帮助学生回顾其他课程的相关内容。据观察,学生往往对实用性强的课程表现出极大的兴趣。融入对比手法的Matlab课程讲授可突显Matlab软件在实际应用方面的便利和强大之处,从而调动学生的积极性和主观能动性。
一 对比手法在Matlab教学中的应用案例
(一) 矩阵的乘法
矩阵的乘法是Matlab的基本算术运算之一。其在《MATLAB程序设计与应用》[10]第2章第5小节中讲到。
首先,我们先讲在线性代数中,矩阵的乘法如何求解。对于两个矩阵A和B,若矩阵A为m行n列的矩阵,矩阵B为n行p列的矩阵,则矩阵C=A×B为m行p列的矩阵,矩阵C中各个元素为这里要注意的是矩阵A的列数要等于矩阵B的行数,矩阵A乘以矩阵B才得以运行。接着,举一个具体的实例。若矩阵则按照上述公式得到矩阵以矩阵C中第一行一列的元素为例,C(1,1)=A(1,1)×B(1,1)+A(1,2)×B(2,1)=1×1+2×4=9。
接下来,对比在Matlab软件中矩阵的乘法如何计算。在Matlab软件中,矩阵乘法用*这个命令,要得到两个矩阵A和B的乘积,需在命令行窗口输入A*B,并按Enter键,即可得到结果。以上述实例(一)中的矩阵A和B为例,具体命令如下:
>> A=[1,2;3,4];
>> B=[1,2,3;4,5,6];
>> C=A*B
C =
9 12 15
19 26 33
(二) 矩阵的逆
逆矩阵是矩阵理论中很重要的内容,逆矩阵的求法自然也是线性代数研究的重点内容之一。在《MATLAB程序设计与应用》[10]第3章第2小节中,讲到矩阵的逆:对于一个方阵A,若存在一个与其同阶的方阵B,使得为单位矩阵,则称B为A的逆矩阵,A也为B的逆矩阵。
首先,我们先讲解线性代数中矩阵的逆如何求解。对于任一二阶方阵其逆矩阵A*是方阵A的伴随矩阵,A*为方阵A的余子式M的转置。为方阵A的行列式的值。方阵A的余子式同样地,给出一个实例,对于方阵先求出方阵A的余子式即得方阵A的伴随矩阵接着求出方阵A的行列式的值可得到方阵A的逆矩阵
下面,我们对比在Matlab软件中矩阵逆的求法。在Matlab中,矩阵逆可用一个命令inv求出。在命令行窗口,我们输入inv(A),并按Enter键,即可得到结果。以上述实例(二)中的方阵A为例,具体命令如下:
>> A=[1,2;3,4];
>> inv(A)
ans =
-2.0000 1.0000
1.5000 -0.5000
(三) 非齐次线性方程组的求解
在《MATLAB程序设计与应用》[10]第3章第2小节中讲到了非齐次线性方程组的求解。线性方程组是指由n个方程构成的线性方程组:
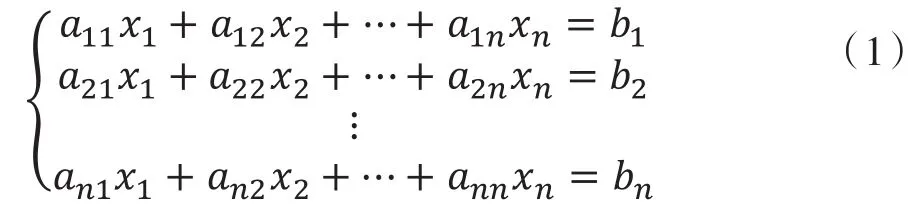
当b1,b2…bn不全为零时,为非齐次线性方程组。其中为系数矩阵,非齐次线性方程组可表示为Ax=b,在其左右两边各左乘系数矩阵的逆矩阵A-1,得x=A-1b,即非齐次线性方程组的解可由系数矩阵A的逆矩阵乘以b得到。
接着我们对比在Matlab中非齐次线性方程组是如何求解的。由实例(一),我们知道在Matlab软件中,矩阵的逆使用命令函数inv。由实例(二),我们知道Matlab软件中,矩阵的乘法使用命令*。因此,我们在命令行窗口输入x=inv(A)*b,即可得到非齐次线性方程组的解。以上述实例(三)中的非齐次线性方程组为例,具体命令如下:
>> A=[1,2,3;1,4,9;1,8,27];
>> b=[5;-2;6];
>> x=inv(A)*b
x =
23.0000
-14.5000
3.6667
(四) 齐次线性方程组的求解
当线性方程组(1)中的b1,b2…bn全为零时,为齐次线性方程组。当系数矩阵A经过初等行变换所化到的行阶梯形矩阵的非零行行数小于A的列数时,齐次线性方程组有非零解。与非齐次线性方程组不同,齐次线性方程组的解不能运用系数矩阵A的逆矩阵来求解。给出一个实例,讲解齐次线性方程组的求解方法。若一个齐次线性方程组为其系数矩阵求该齐次线性方程组的解,先对系数矩阵A进行初等行变换,分别进行将矩阵A中的第三行减去四倍的第一行,第二行减去二倍的第一行,得接着将第三行减去第二行得此矩阵是最简化的系数矩阵,其对应的方程组为令z=k,k为任意实数,原齐次线性方程组的解为
接着我们对比在Matlab中,齐次线性方程的解如何求得。在命令行窗口输入x=null(A),即可得到齐次线性方程组的非零解。值得注意的是,齐次线性方程组存在多组非零解,用Matlab求解,只可得到其中一组非零解。以上述实例(四)中的齐次线性方程组为例,具体命令如下:
>> A=[1,2,-1;2,3,1;4,7,-1];
>> x=null(A)
x =
-0.8452
0.5071
0.1690
(五) 矩阵的特征值与特征向量
在《MATLAB程序设计与应用》[10]第3章第4小节中讲到了矩阵的特征值与特征向量。对于n阶方阵A,若Aξ=λξ成立,则λ和ξ是方阵A的特征值和特征向量。等式Aξ=λξ等价于(A-λI)ξ=0,I是单位矩阵。若使方程(A-λI)ξ=0有非零解,则其系数行列式|A-λI|必须等于0。
接着我们对比在Matlab中,方阵的特征值与特征向量如何求得。在Matlab中,我们用eig函数求方阵的特征值和特征向量,其调用格式为[X,D]=eig(A),D是一个对角阵,其对角线上的元素为方阵A的全部特征值,X是与D同阶的方阵,其各列是对角阵D中各特征值相应的特征向量。值得注意的是,方阵A在某一特征值下对应多组特征向量,用Matlab求解,只可得到其中一组特征向量。以上述实例(五)中的方阵A为例,具体命令如下:
>> A=[2,1;3,0];
>> [X,D]=eig(A)
X =
0.7071 -0.3162
0.7071 0.9487
D =
3.0000 0
0 -1.0000
(六) 多项式求根
在《MATLAB程序设计与应用》[10]第6章第2小节中讲到了多项式求根。多项式是指由若干个单项式相加组成的代数式,其形如以2次多项式为例,2次多项式形如在数学上,我们一般用配方法来求其根,其两个根分别是举一个实例,对于2次多项式用配方法可得其两个根分别是x1=1.099和x2=-9.099。
下面,我们对比在Matlab软件中如何计算多项式的根。在Matlab软件中,我们可以用三种方法来计算多项式的根,其中最简单的一种是运用命令函数roots。值得注意的是,在Matlab中,多项式可由一个行向量表示,其各个元素分别为各个单项式的系数,并且按照从高次幂依次往低次幂排布。以上述实例(六)中的2次多项式为例,具体命令如下:
>> P=[1,8,-10];
>> x=roots(P)
x =
-9.0990
1.0990
第二种计算多项式的根的方法是利用多项式的伴随矩阵求得。多项式的伴随矩阵对应的特征值,即为多项式的根。在Matlab中,我们运用函数compan求多项式的伴随矩阵。在实例(五)中已讲到用eig函数求某方阵的特征值。该方法的具体命令如下:
>> P=[1,8,-10];
>> A=compan(P);
>> x=eig(A)
x =
-9.0990
1.0990
第三种计算多项式的根的方法是利用到《MATLAB程序设计与应用》[10]第5章第1小节中讲到的二维图形绘图法。我们可以提供一组x坐标,并将其带入多项式中。令多项式的值为y坐标,绘制分别以x和y为横、纵坐标的二维曲线。这条二维曲线与y=0曲线的交点即为多项式的根。该方法的具体命令如下:
>> x=[-15:0.1:15];
>> p=x.^2+8*x-10;
>> figure
>> plot(x,p)
>> grid on
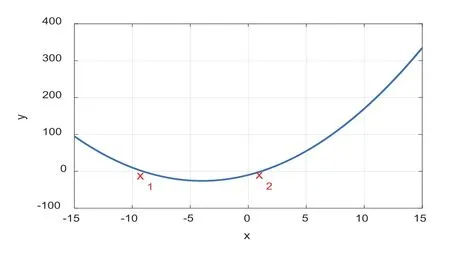
图1 实例(六)中的2次多项式y=x2+8x-10
从以上六个实例看出,运用Matlab软件后,很多在数学中较为复杂的解法变得简洁,方便。通过将数学解法与Matlab的命令操作进行对比,使得学生深入地理解了Matlab每条命令的意义,便于学生记忆Matlab的基础语言和命令。
二 效果评价
Matlab课程包括理论讲授和上机实验操作两部分。在Matlab理论讲授过程中引入对比手法,经过近几年的课程实践,从学生的反馈来看,课程得到了认可,学生的学习热情得到了激发。很多学生反馈,对比某一运算的数学解法和其在Matlab中的命令操作,帮助他们理解每条命令的具体含义,并加速他们对Matlab基础命令的记忆。并且,在上机实验操作时,他们不再是机械化地敲命令,而是会思考和分析命令运行后得到的结果。此外,Matlab课程安排在高等数学,线性代数,矩阵论等课程之后,该教学方法还帮助他们复习了相关课程中的知识要点。
三 结语
本文针对Matlab基础语言和命令讲解中存在的问题进行分析,提出应用对比手法,通过对比Matlab的命令操作及其数学解法,加深学生对Matlab命令的理解。经过近几年的不断摸索与实践,课程得到了学生的认可,学习热情得以提高。在接下来的教学过程中,将进一步优化教学内容,更加深入地探索有利于培养学生自主性,创新性以及解决问题的能力。

