玻璃格栅对半刚性基层抗裂性能的影响研究
黄 睿 田鑫雨
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000;2.浙江省岩石力学与地质灾害重点实验室,浙江 绍兴 312000)
0 引言
我国公路结构普遍采用半刚性基层与沥青面层结合的方式[1].在车辆荷载作用下,道路结构往往会产生裂缝,而道路病害又以结构开裂为主.半刚性基层开裂的机理复杂、危害程度高,裂缝类病害对路面破坏的贡献率达到91.7%[2].孙斌[3],刘晓华等[4]对基层损坏状况进行了研究,并提出了相应的维修对策和质量评估方法.祝争艳等[5],王复明等[6]通过改良聚合物注浆材料和修补方式,提高了基层裂缝的修复技术.半刚性基层裂缝防治的研究大多针对基层病害的修复和基层的抗压强度[7-12],对于基层在车载作用下受拉开裂的研究较少,且大部分研究只考虑了静载的状态,较少考虑频率荷载的作用.
玻璃格栅作为一种新型土工材料,因其拥有较好的抗拉强度,逐渐被应用于道路工程中[12-18].然而玻璃格栅在公路中的应用大多集中在路面的抗反射裂缝上,缺乏玻璃格栅布置对于半刚性基层抗裂方面的研究.从抗反射裂缝的效果来看,将其应用于道路结构能有效改善半刚性基层的开裂问题.
本研究基于数值模拟的方法,对比等频率标准轴载作用下在面层铺设不同深度玻璃格栅后基层的应力应变情况,并对车载作用下半刚性基层抗裂性能的提升提出建议.
1 数值建模
1.1 弹性层状理论模型
本研究拟采用弹性本构模型来表征沥青路面结构各层混合料的材料参数,结构模型如图1所示.

E1μ1h1E2μ2h2………En-1μn-1hn-1Enμnhn
1.2 模型基本假定
(1)模型结构中各层材料均匀、各向同性;
(2)模型结构中各层间接触状态为硬接触;
(3)模型结构中路基为半无限体;
(4)层间接触状态恒定,切向罚值恒为0.5,不随加载过程改变;
(5)忽略模型段以外路段对模型的力学计算影响.
1.3 数值模型
数值模型为三维有限元模型,道路结构分为路基、底基层、基层和沥青面层四部分.其中,模型长度为8 m,宽度为4 m,厚度为1.58 m,其中面层厚度为0.18 m,基层厚度为0.22 m,底基层厚度为0.23 m,路基厚度为0.95 m.模型各层之间相互作用类型为法向硬接触,用“罚”来定义切向摩擦系数,罚值定义为0.5.模型下边界设置竖向约束,其他表面自由,材料力学参数见表1.除传统的四层结构模型外,设置三个相同计算模型,并在三个计算模型面层中设置玻璃格栅应力消除层,应力消除层厚度为0.02 m,宽度为4 m,长度为8 m.各应力吸收层空间位置(距路面距离)分别为0.10 m、0.14 m和0.18 m.
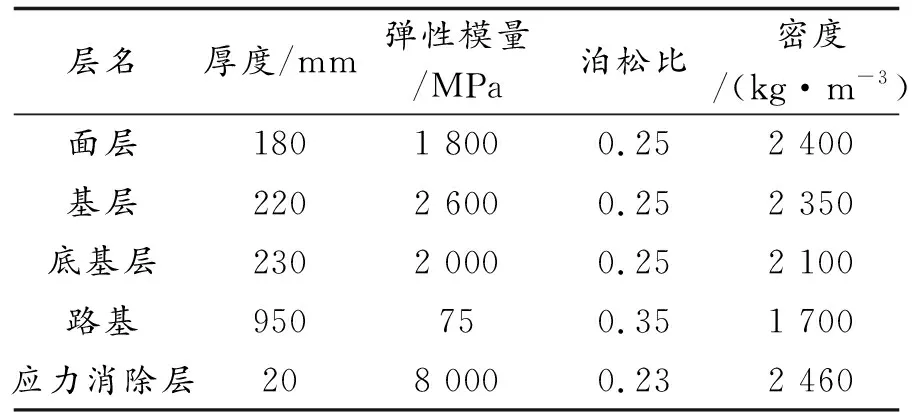
表1 各层材料力学参数
为考虑车载作用对半刚性基层开裂的影响,在面层设置两条车辙作用区域(0.1 m×8 m),在车辙区域施加设计轴载100 kN, 两条车辙间距1.4 m.为真实模拟行车作用,荷载设定固定的频率,每隔0.1个时间长度在0~100 kN之间切换一次,加载24个时间长度.计算模型如图2所示.

图2 计算模型
2 不同工况下应力分析
2.1 计算工况
为更好地分析计算结果,对不同计算模型进行工况分类.
工况一:无玻璃格栅应力消除层;
工况二:玻璃格栅应力消除层设置在路面以下0.18 m处;
工况三:玻璃格栅应力消除层设置在路面以下0.14 m处;
工况四:玻璃格栅应力消除层设置在路面以下0.10 m处.
2.2 计算结果分析
2.2.1 玻璃格栅的影响
对比传统路面结构和玻璃格栅路面结构中半刚性基层的上、下表面拉应力水平,以工况一和工况二为代表.选取两个工况计算结果中x方向上的水平应力分量S11进行分析,应力云图如图3所示.

(a)工况一上表面 (b)工况一下表面
从应力云图中可以看出两种工况下基层下表面基本都处于受拉状态,基层上表面纵向中间位置处于受拉状态,两端位置部分处于受压状态.可见在车载作用下,半刚性基层下表面更容易受到拉应力的影响,而上、下表面的中间部分相较其他位置也更容易产生拉应力集中,从而产生破坏.
对比两种工况拉应力的分布情况,可以观察到工况一比工况二表现出更明显的应力集中现象,而且工况一中应力最大值大于工况二中的应力最大值.所以两种工况相对来说,工况二应力分布均匀、拉应力值较小,更加安全;工况一应力集中,拉应力值较大,容易出现不利位置,产生受拉开裂.
2.2.2 四种工况应力值对比分析
应力云图只能大致从应力分布情况观测各工况的宏观水平,现对应力云图中拉应力主要集中部位选取节点路径,并对各个节点进行相关数据提取:
路径一:基层上表面车辙正下方;
路径二:基层上表面z=2 m位置;
路径三:基层下表面车辙正下方;
路径四:基层下表面z=2 m位置.
路径一中工况一的应力水平略高于其他几种工况,而其他几种工况的应力水平基本相似;在路径二中各个工况出现了一些差别,其中工况二在同一条路径的相同位置处拉应力水平最低,工况一的拉应力水平最高.从上表面的两条路径结果来看,铺设玻璃格栅对基层的抗裂性能有一定的改善作用,其中工况二的效果最优.
结合图3和图4可以看出,基层下表面大部分处于受拉状态,各个工况的拉应力差距比上表面更加明显.对选取的两条下表面路径进行分析发现,铺设玻璃格栅的三个工况拉应力明显较低,而在这三种工况中,工况二和工况一的差别最大,特别是在路径二和路径三中各工况的拉应力水平得到了极大改善.在x=4 m时,路径三中工况二、三、四的S11应力值分别下降了0.11 MPa、0.06 MPa和0.07 MPa,相较其他两种工况,工况二的优化程度有了近2倍的提升.结合上表面两条路径的分析结果,从S11应力分布角度来看,将应力消除层铺设在面层底部可以达到最优的抗裂效果.
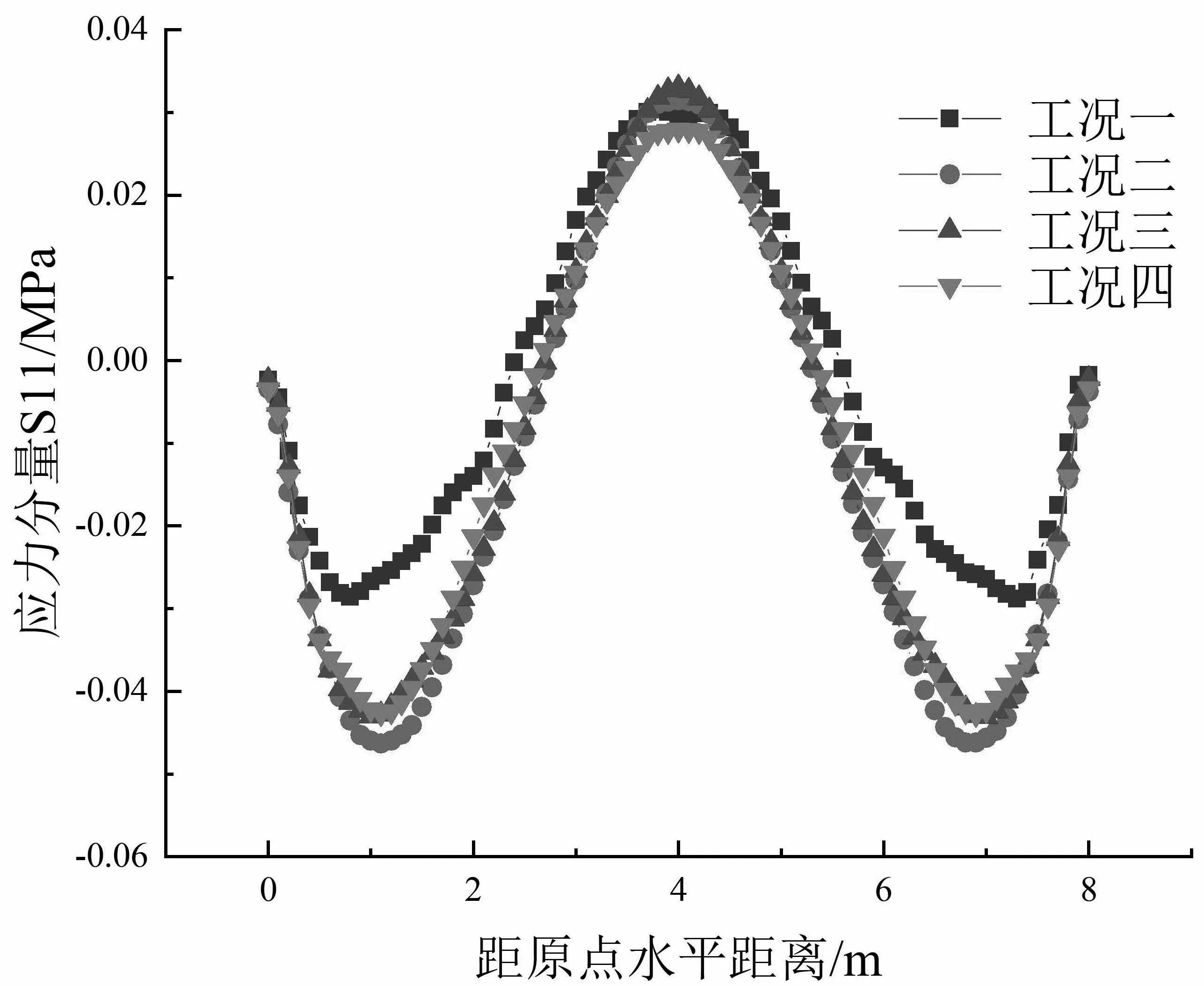
(a)路径一 (b)路径二
从云图中的应力分布状态可以看出,路径二和路径三的拉应力最大.对两条路径的中间部位选取节点,并按加载时间对所选节点进行应力数据提取,用来描述四种工况在相同加载方式下的拉应力变化.从图5可以看出应力值随着加载时间的增长呈现波动上升的趋势,同时工况一中S11应力分量的上升速度快于其他三种工况,各工况下应力峰值的出现时间分别为20.4 h、22.8 h、22.3 h和21.6 h,证明铺设玻璃格栅有利于提高基层的疲劳寿命.其中,其他三种工况的峰值时间相较于工况一分别延迟了2.4 h、 1.9 h和1.2 h,抗疲劳优化程度也提升了2倍.
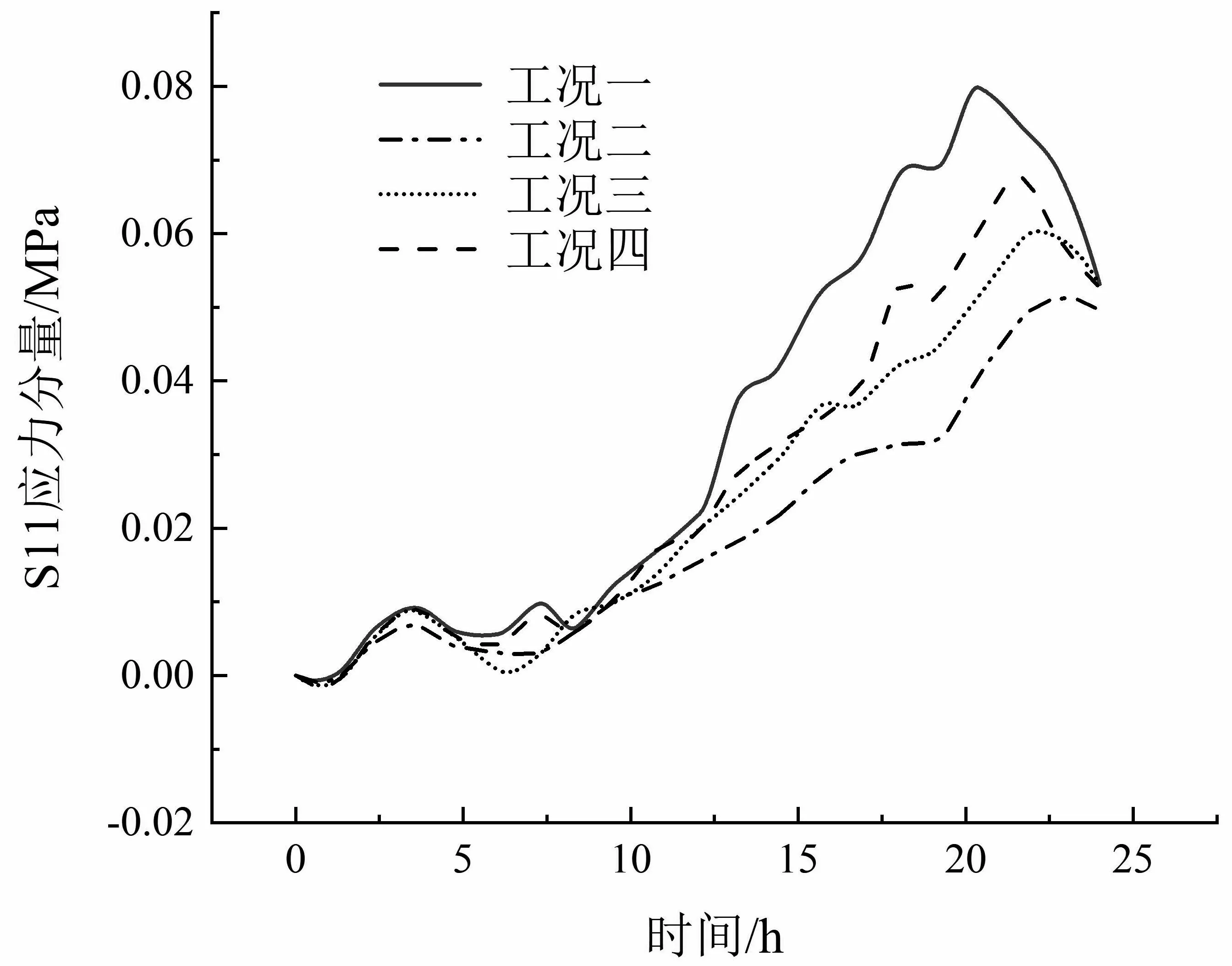
(a)路径二 (b)路径三
3 弯沉值和节点横向位移
弯沉值是研究基层开裂的重要参数,本次模拟中基层弯沉主要集中在两条车辙的中间部分.因此,选取上表面弯沉区域的边缘和中心位置(路径一和路径二)来进行分析,在两条路径的中心位置选取节点,并将节点竖向位移数据U2进行提取作为弯沉值的表征(见图6).从图6可看出在铺设玻璃格栅对于道路的弯沉有一定的优化,但工况二、工况三和工况四的弯沉曲线基本重合,差异性很小,并不能得出玻璃格栅空间位置的明显规律,这可能和路基的竖向边界条件有关.
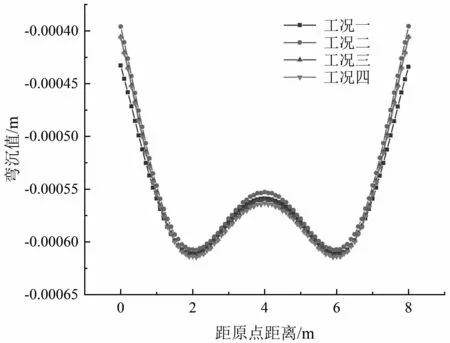
(a)路径一 (b)路径二
基层的荷载型裂缝主要是由于结构在车载作用下产生的弯拉现象,弯拉的表现形式除弯沉外,还有基层的纵向变形程度。所以对上述路径中各节点的水平位移值U1进行提取,用各节点的水平位移值来表征基层的变形程度, 如图7所示.
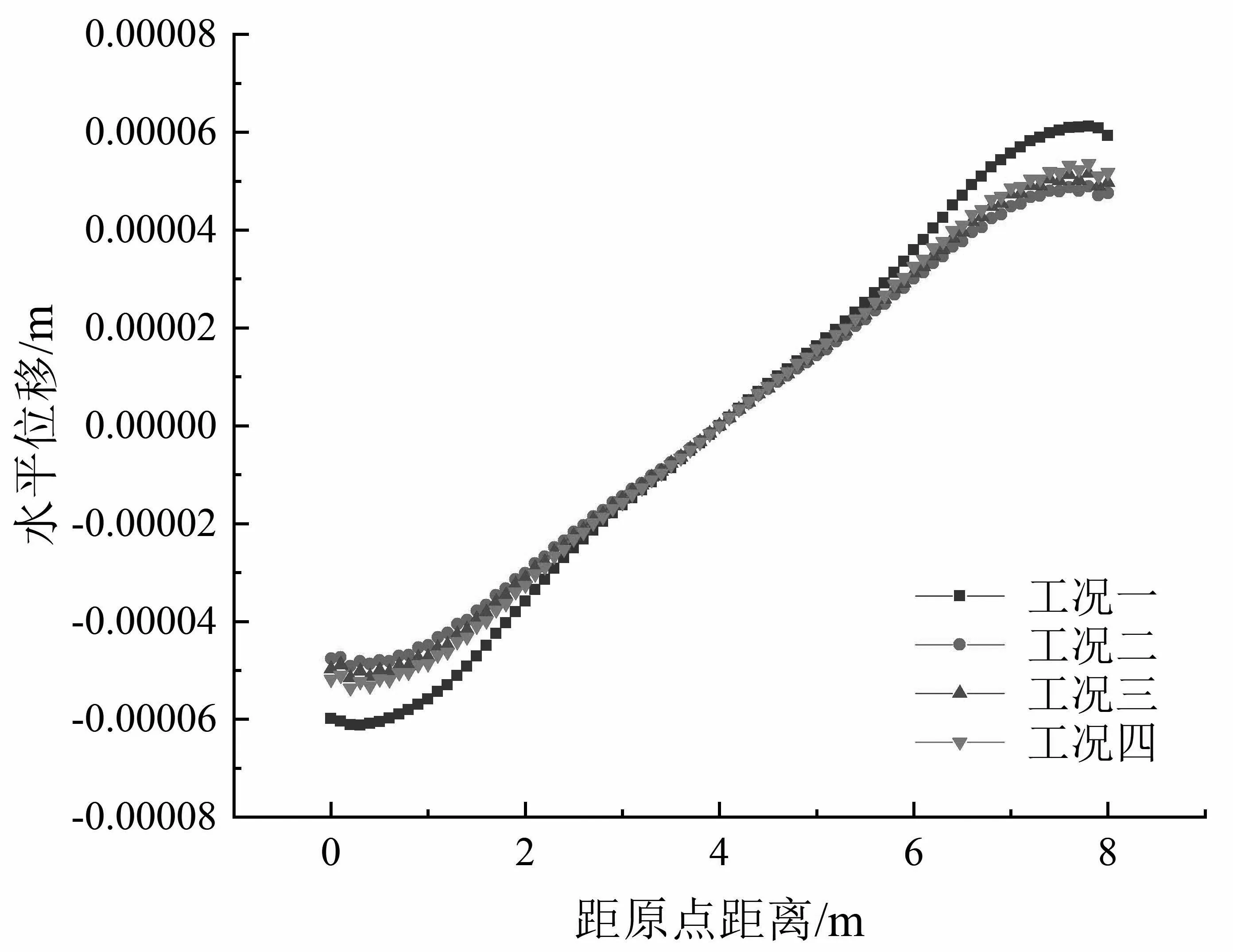
(a)路径一 (b)路径二
相对于弯沉值,节点水平位移可以更加直观地显示出四种工况的优劣.从图7可以看到两条路径上节点的水平位移值呈轴对称形式,随着距道路两端距离的减小,水平位移值呈线性增长,且各工况差异性也随之增大.所以随着基层结构到中心位置距离的增加,玻璃格栅对基层抗裂性能的优化越明显,特别是工况二(玻璃格栅设置在基层面层接触面位置)最优.
此外,由于未对层状结构的两侧施加位移边界条件,模型表现出道路两端位移值最大,出现最不利位置的现象.在实际中路基和底基层作为半无限体,在一定范围内并不会出现两端自由的情况,而基层在粘结和摩擦作用下,水平方向上也会受到一定的约束,即基层的两端实际上也存在一定的边界约束.所以在层间粘结性能一定的情况下,参照以上的应力分析结果,基层的最不利位置可能会位于基层中间.
4 结论
本文通过数值模拟研究了车载作用下玻璃格栅对半刚性基层抗裂性能的影响,选取了四种玻璃格栅铺设工况,对比分析了各工况基层上、下表面的应力水平,以及上表面的弯沉值和水平位移大小.主要得到以下结论:
(1)基层开裂本质上是基层内部拉应力的发展结果.随着车载的周期作用,道路材料各部分的应力水平进行了重分布,拉应力主要集中在基层上、下表面中部位置和下表面车辙位置.随着加载时间的增长,应力值也波动性的增长,直到基层产生疲劳破坏.
(2)设置玻璃格栅对半刚性基层的抗裂性能有一定的改善,特别是拉应力水平和基层的变形情况.当玻璃格栅铺设在半刚性基层和沥青路面接触界面时,半刚性基层的应力水平和变形程度最低,相较其他的铺设位置,工况二的抗裂优化程度可达到近似2倍的程度.
(3)设置玻璃格栅对半刚性基层的抗疲劳性有一定改善.在周期荷载下传统道路结构的应力增长过程波动幅度大、频率高,铺设玻璃格栅的路面结构,基层应力水平相对平稳增长,能有效提高基层的疲劳寿命,且铺设位置位于基层和面层接触面时优化效果最好,对比其他铺设位置最大存在2倍的抗疲劳提升效果.

