基于动网格的隧道通风井合理倾角研究
薛大鹏 郑国平 郭洪雨 庄一舟
(1.绍兴文理学院 土木工程学院,浙江 绍兴 312000;2.浙江工业大学 土木工程学院,浙江 杭州 310014;3.浙江省交通规划设计研究院有限公司,浙江 杭州 310030)
0 引言
隧道作为相对封闭的人造空间, 汽车在行驶过程中释放出大量的污染物. 对于地理位置复杂、 长度较长的隧道, 出入口自然通风的模式会出现通风不足的情况, 从而导致污染物浓度的升高. 竖井型自然通风是指在隧道顶部设置连接地面的通风竖井, 借助交通风压来实现隧道通
风的模式. 目前已在成都市红星路下穿隧道(800 m)、南京市通济门隧道(890 m)、西安门隧道(1 410 m)、杭州市彩虹路隧道(3 260 m)等工程中开展应用.
国内外已开展众多针对这一新型通风模式的研究,为工程建设提供了理论基础.如,Yoon等[1]曾利用热动力方法,对韩国某长公路隧道冬夏季竖井自然通风压力进行测量,发现有通风竖井的隧道自然风压远大于无竖井的隧道,证明了竖井型自然通风的可行性;Chen等[2]通过模型实验对车辆产生的活塞风分布等因素进行了研究,提出了隧道活塞风的相应参考理论;Sambolek[3]通过控制模型车辆的车速来研究可工况下的交通风速与风量,证明了自模区临界雷诺数的存在;童艳等研究了污染物扩散与竖井间距、截面尺寸、交通量、车速和主体长度之间的关系,建立了隧道污染物的扩散方程[4],提出污染物的量可通过车速和主体长度的调节来实现改善[5];朱培根等对有害气体浓度分布进行了研究,通过建立分布模型提出对隧道卫生效果的评价方法[6],并采用缩尺模型研究南京中山东路隧道阻滞工况下的交通风压及通风效果[7].
然而,竖井型自然通风呈现的是非恒定的稳流状态,这是由于车头附近为压力波峰(正压),车辆后方为压力波谷(负压),隧道内空气被挤出竖井后尚来不及扩散又被吸入隧道,形成“气流短路”.Jaroslav等[8]应用欧拉-拉格朗日模型模拟了汽车在隧道内的运动及其对隧道通风的影响,提出交通引起的湍流对隧道内总流量有不可忽略的影响.Aydin等[9]模拟了在有限空间内物体平移而产生的拖拽流动,为汽车在隧道内运动研究提供Couette流动的理论.金斯科等[10]利用1∶10的模型实验平台研究了通风竖井内的气压脉动规律,发现其振幅随竖井高度增加而降低.由于汽车运动等因素使得隧道内气压较小时,通风竖井容易受隧道外大气压环境的影响而产生风向的频繁波动,即竖井型自然通风隧道的“哮喘效应”.这一问题导致实际每组竖井的换气量无法量化,隧道沿程污染物浓度无法得到解析解,也就无法判断隧道内空气质量是否满足相关规范要求.为了解决这个问题,拟采用数值模拟结合模型实验手段,通过改变通风竖井的倾斜角度来获得恒定的气流,以实现一组井口主要排风,另一组井口主要吸风的人为组织通风模式,从而获得隧道污染物沿程浓度分布,以提高竖井型自然通风隧道的通风效率.
1 工程背景
以G228宁波西店湾隧道为背景工程, 该隧道为总长1 590 m的双向六车道一级公路隧道, 设计车速为80 km/h, 2020年的预测交通量为11 325 Pcu/d, 2035年的预测交通量为21 032 Pcu/d,车型构成比例如表1所示.

表1 车型构成比例表
高峰小时交通量系数取为0.11,方向不均衡系数取为0.52, 折算混合车与标准车系数约为1.85,据此可以计算出远期单孔隧道内有13辆车.
由于周边小区对环境控制要求很高,同时,为了避免采用轴流风机引起的噪音问题,拟在环境敏感区范围外设置两组自然通风竖井.第一组通风竖井起点设置在距离隧道入口795 m处,第二组通风竖井起点距离隧道入口1 095 m,井段长55 m.每组通风竖井分别由五口通风竖井组成,井口长度7 m,宽度2.5 m,井高3.5 m(井口至隧道结构内表面的垂直距离),井口中心间距12 m,自然通风竖井投影面积17.5 m2.
2 基于FLUENT动网格模拟
2.1 模型建立
基于动网格技术利用FLUENT软件对原型隧道建模,选取k-ε湍流模型进行分析.为了便于分析通风情况,将常温下隧道内低速流动的气流视作不可压缩的连续介质流体.采用整体建模,隧道区域长1 590 m,入口处边界条件为压力入口,隧道出口及通风竖井井口的边界条件为压力出口,隧道壁面的沿程摩阻系数为0.02.模型中共设有13辆车依次驶入隧道内,前后车间距为66.6 m,车队总长803.2 m.车队完全通过一组通风竖井所需要的时间为38.66 s.车头与车位为壁面边界条件,通过UDF宏赋予其固定的移动速度,车身侧面作为滑移动网格交界面与隧道内部空气进行数据传递.根据隧道实况来建立隧道截面与通风口位置大小,模型整体示意图如图1.
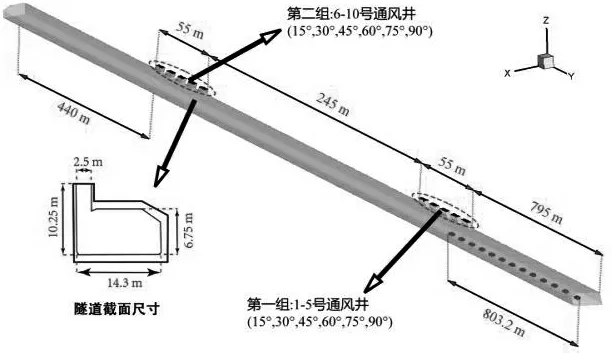
图1 模型整体示意图
2.2 隧道活塞风速的模拟分析
行驶的车辆作为隧道内的压源,是产生交通活塞风的直接原因.以90 °通风竖井隧道为例,隧道通风竖井段在交通活塞风作用下,第一组通风竖井纵截面的风速分布如图2,通风竖井横截面风速分布如图3.
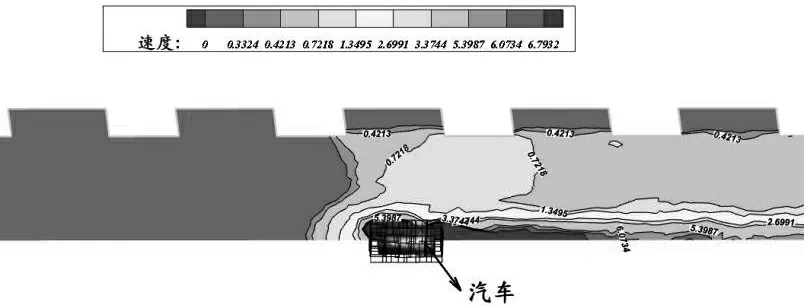
图2 通风竖井纵截面风速等值线分布图
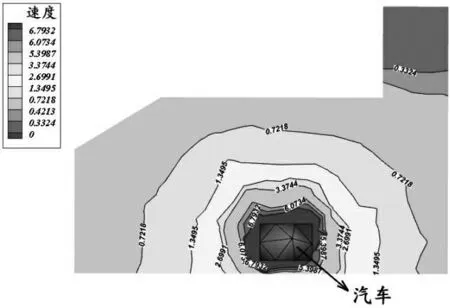
图3 通风井横截面风速等值线分布图
计算结果的速度云图显示,整个隧道断面风速分布不均匀,车辆带动靠近路面处的风流加速,使隧道下半部分的断面平均风速达到了5 m/s~6 m/s.图2中所选断面靠近隧道侧面墙壁,故整体风速偏小;图3中所选断面为中间车道处,断面内风速不均匀,靠近地面车辆的位置,前后两车之间断面的气流平均风速在6~8 m/s左右,而隧道上半部分风速较小,仅有1 m/s左右.隧道内部在平稳的交通通风力作用下的横断面平均风速为5 m/s左右.
图4为隧道内距离入口200 m处的横断面平均风速变化情况.从图中可以发现:车队在通过该截面时,通风井处空气流速波动呈现周期性,单个周期时长约为3.0 s;当车队中的前四辆车经过断面时,断面风速呈波动式上升趋势(图中I区);第四辆车到达断面处时,断面风速已经基本达到计算风速,且车辆驶过时,隧道内空气由于受车辆的挤压,断面风速在计算风速附近震荡(图中II区);当车队最后一辆汽车驶离该断面后,断面风速迅速下降(图中III区).
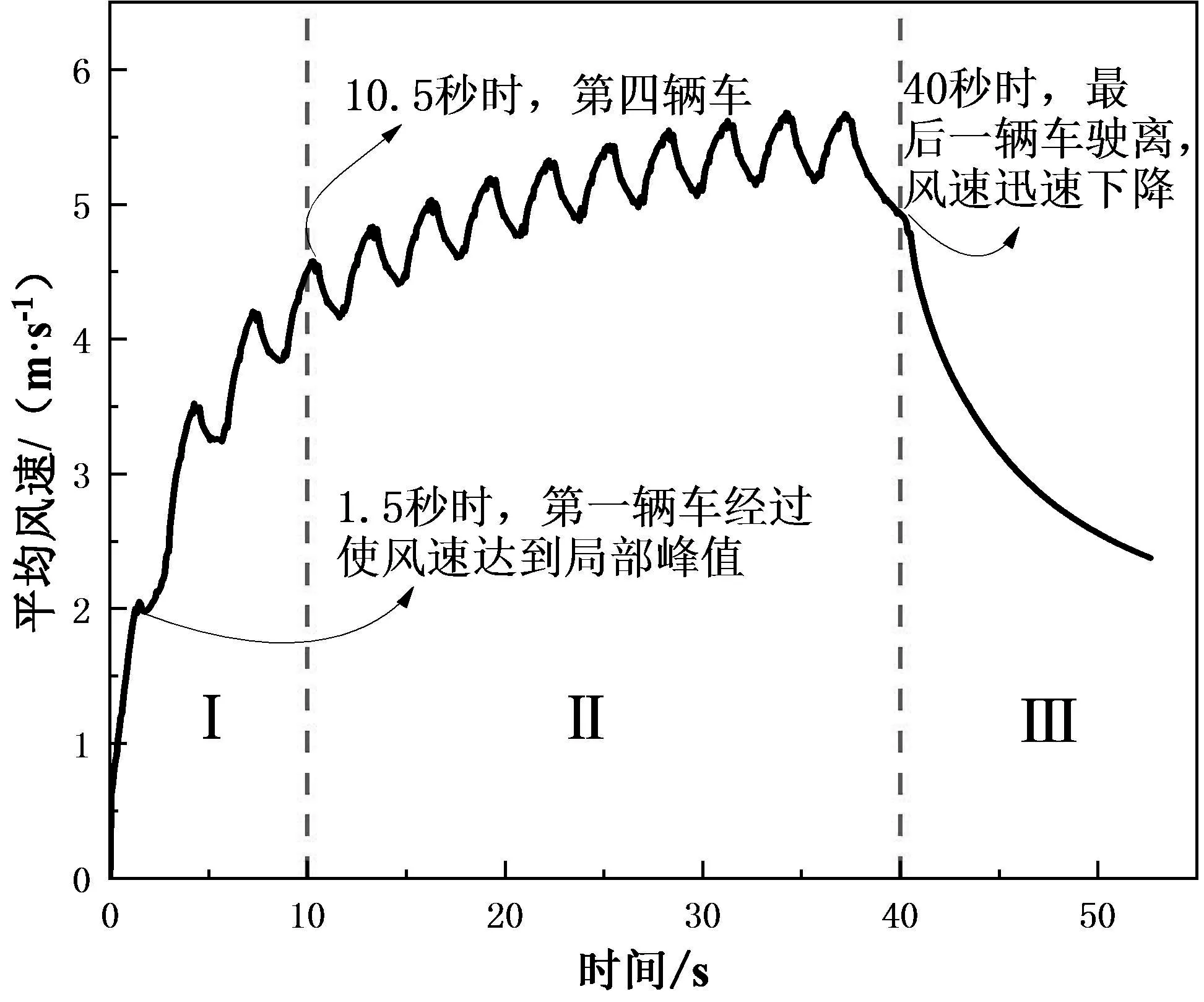
图4 隧道内部横截面平均风速变化图
2.3 通风井角度对进排风速的影响分析
当车队通过某一组通风井时,对通风井井口处的空气流速数据进行提取,取该段时间内的平均流速作为该组通风竖井在交通活塞风作用下的通风风速vi,i=15、30、45、60、75、90.
以15 °通风竖井隧道为例,流速取向外流出为正,向内流进为负,各通风竖井的流速如图5、图6.
从图5、图6可以看出:
(1)靠近上游的第一组通风井和靠近隧道下游的第二组通风井由于所处位置不同,车辆所产生的交通活塞风对其影响也不同.第一组通风井表现为出风状态,而第二组为进风状态;
(2)图中均值线的值为各通风井口Ⅱ区域相应时间内的平均流速.对于第一组通风井,车队
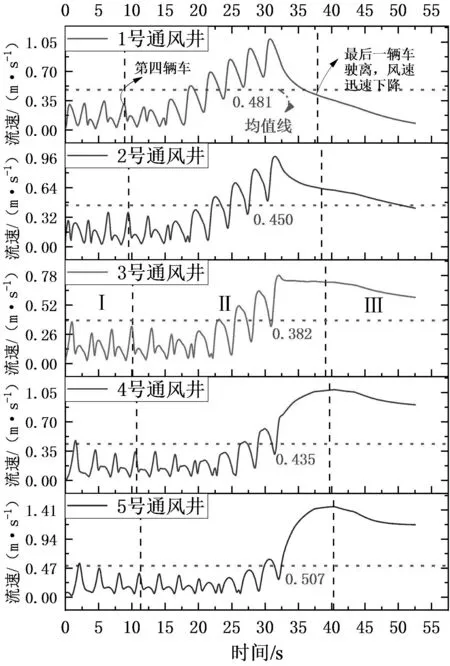
图5 第一组通风井流速 图6 第二组通风井流速
从1号井至5号井依次经过,五个井口的平均流出速度先减小后增加;而车队经过第二组通风井时,五个井口的流进速度逐渐增加;
(3)由于车辆行至第一组通风井时隧道内尚未形成具有一定规模的活塞风,而行至第二组通风井时活塞风已得到充分发展,所以第二组通风井的流速随时间变化相对第一组更为平稳.
通风井角度为30 °时,随着车队的经过,两组通风井口流速规律与15 °时一致,但平均流速要小于15 °时.通风井角度为45 °、60 °、75 °、90 °时,气流方向与15 °时相反,为向外流出,并且随着车队的经过,两组通风井的平均流速均呈现先减小后增加的规律.
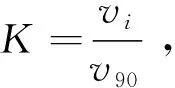
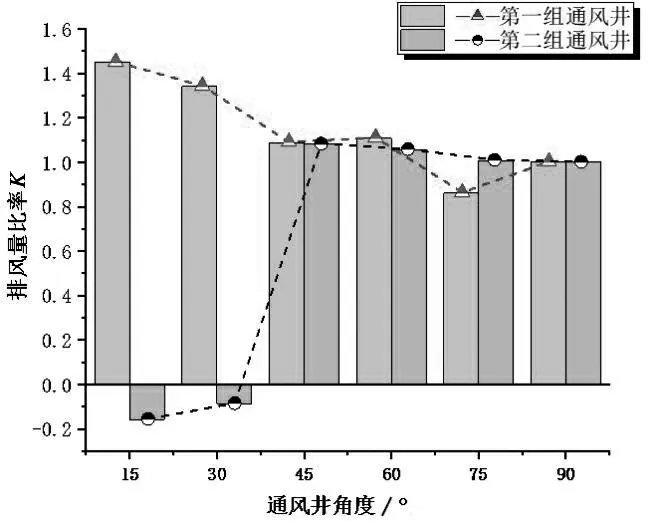
图7 两组通风井的排风量比率K随角度变化图
通风井角度为90 °时,第一组和第二组流速均为正,为向外流出状态.根据结果,第一组通风竖井在任意角度下,K值均为正,即气流方向与90 °时一致,说明在车队经过的过程中,通风井始终保持排风状态.比率K随着通风井角度的减小而呈现递增的趋势,说明第一组通风井角度越小,单位时间内的排风量越大,即越有利于排风.
对于第二组通风井,15 °时与30 °时K值为负,且前者的绝对值大于后者,说明在车队经过的过程中,15 °与30 °的通风井均保持进风状态,前者单位时间内的进风量比后者更大,更有利于进风.45 °、60 °、75 °和90 °时K值为正,说明在车队经过的过程中,通风井为排风状态.
3 自然通风效果模型实验
3.1 交通活塞风的确定
交通活塞风是指汽车在管状隧道中由于活塞效应带动空气向前运动所引起的通风动力.基于流体力学能量守恒定律及交通流为稳定流的假设,当交通通风力与通风阻抗力相等,所对应风量即为交通活塞风量,交通活塞风量可通过交通通风力引起隧道内的活塞风速vr来求得[11].交通通风力Δpt(N/m2)的计算公式:
(1)
另一方面,隧道内空气流通所受到的通风阻抗力Δpr(N/m2)的计算公式如下:
(2)
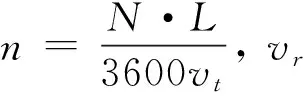
根据Δpr=Δpt,可求得隧道内风速vr.对于顶部设有多处通风口的自然通风隧道,钟星灿等学者[12]提出了一种基于隧道内流体动量、能量、质量守恒定律的计算方法,计算结果表明,当隧道内车速条件为60 km/h,车流量为定值时,隧道各分段风速在5 m/s至6 m/s范围内变化.
因此,以西店湾隧道为例,参照《公路隧道通风设计细则》汽车截面积,小客车的断面积为2.13 m2,大车的断面积可取5.37 m2.根据车型比例算得当量汽车截面积2.8 m2,长度6 m,在隧道内行驶速度为80 km/h,可以得到原型隧道在交通风压作用下隧道内的理论空气流速vr=5.06 m/s.该结果与数值模拟中得到的交通通风力基本一致.
3.2 实验模型
模型实验采用1∶20的几何相似比,选用金属板与角铁作为材料对模型进行分段制作,模型隧道横截面尺寸为71.5 cm×33.75 cm,通风竖井高17.5 cm,开口尺寸12.5 cm×35 cm.制作完成后通过螺栓对分段箱体进行初步连接,随后在连接处贴上透明胶布以保证模型气密性.通风竖井部分单独进行制作,可通过同样的方法安装在分段箱体顶部开口处,且易于拆卸,隧道和通风竖井模型与风速测点位置如图8和图9.

图8 隧道模型与截面测点位置图(单位:cm)

图9 通风竖井模型和测点位置图(单位:cm)
模型隧道长度为18.5 m,实验中以隧道原型的计算活塞风速作为实验参考风速,并用格栅网的局部阻力模拟缩减部分的沿程损失[13].
因本研究主要研究对象为通风竖井部分,故实验主要测试不同角度通风竖井对隧道内部气流的分流作用,以及通风井口的流速分布情况.
假设隧道内车流为连续不间断的恒定流,通过数值模拟计算,在顶部设有通风竖井的单向交通隧道中,隧道内部气流的动压部分是呈水平方向的矢量运动,仅有其静压部分对开孔起作用,且顶部开孔面积与隧道的断面积之比较小,无论开孔处产生排出或吸入气流,隧道内不同区域的空气流速仅在理论交通活塞风速值上下浮动.而本实验研究中着重考虑通风竖井的影响,因此采用轴流风机的升压力代替交通风压,以模拟通风竖井在稳定气流作用下的进排风情况(图10).
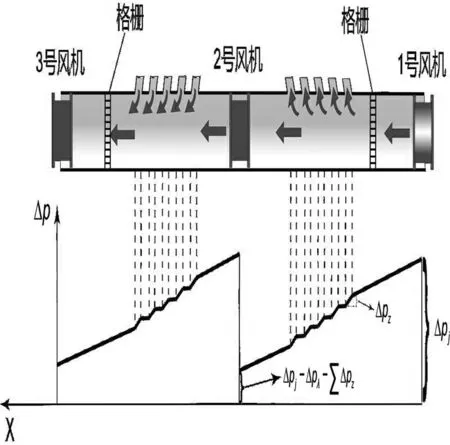
图10 实验风机布置位置及沿程压力变化示意图
现有的模型实验研究中通常采用模型汽车,但这样测得的数据波动较大,且对实验环境要求较高,要尽量减小实验区域的外界气流波动并配合高灵敏度的测量仪器才能保证模型实验的准确性.轴流风机的优势在于它产生的气流速度容易控制,且十分稳定,受实验环境影响小,测量数据稳定.
由于采用了轴流风机代替交通风压,并将风机直接安装在模型内部,模型中断面风速会相对集中于测点4.实验中通过调节风机开关大小来控制断面的平均风速,为1 m/s.
3.3 实验相似性
模型与原型的相似性是实验正确模拟的基础.为了满足气流运动的相似,需要通过模型与原型的Re(雷诺数)相同来实现,即:
(3)
运动黏度ν可以表示为动力黏度μ与流体密度ρ之比.由于模型与原型介质均为空气,则
ρp=ρm
(4)
且常温下,
μp=μm
(5)
故,实验中气流运动相似需要满足
vp∶vm=lm∶lp
(6)
要让模型内气流运动与原型完全相似,则要在模型中产生λ倍于原型的高速气流.现有研究中通常以雷诺数Re大于第二临界值,即气体的流动状态处于雷诺数的自模区内,作为模型内气流与原型气流运动相似的依据,可通过预备实验确定模型的临界雷诺数.
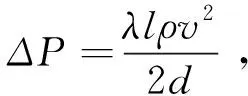
图11为实验模型在不同隧道内空气流速情况下,Re-λ的关系曲线.可以看出当雷诺数大于15 000时,隧道模型的沿程阻力系数基本不再随流速的增加而改变,标志气流已进入自模区.
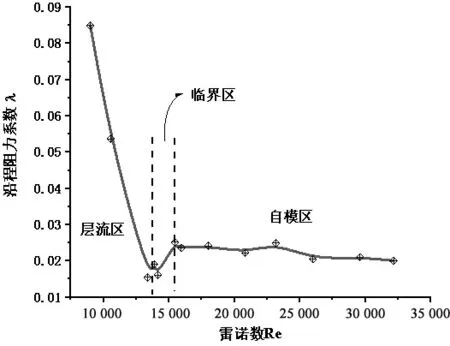
图11 模型隧道的Re-λ关系曲线图
Re=15 000称为临界雷诺数,对应的空气流速vc=0.582 2 m/s称为临界风速,正式实验中要保持隧道内部风速始终在临界风速之上,即可满足模型与原型空气流动的相似.自模区中沿程阻力系数平均值为0.02.
根据实验条件确定了模型实验的基本比尺,主要有:
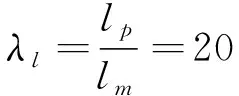
(7)
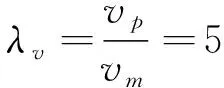
(8)
下标p表示原型参数,下标m表示模型参数.由速度比尺得出模型中交通活塞风风速=1.032 m/s.
根据参数的定义或准则关系,由基本比尺得到其他导出比尺,有:
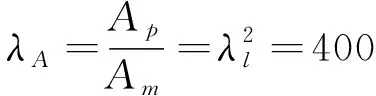
(9)
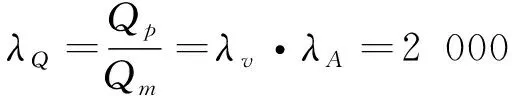
(10)
3.4 实验结果(见图12与表2)
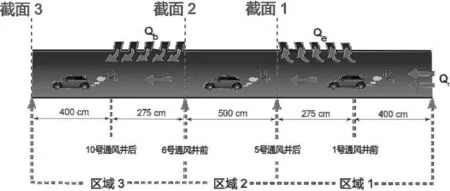
图12 风速测量断面位置
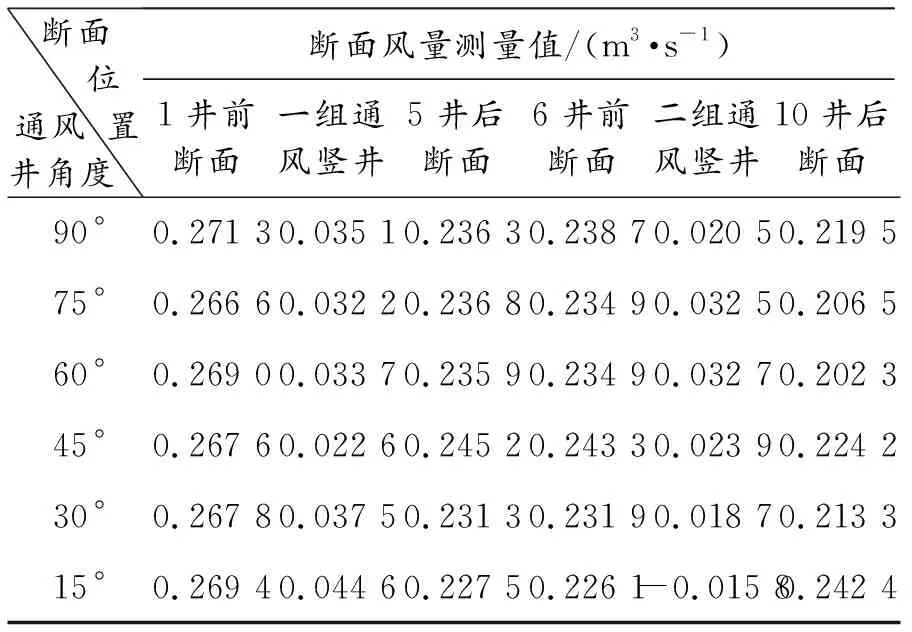
表2 不同角度通风竖井隧道模型风量统计表
当倾斜角度较大时,15 °通风竖井的断面面积较90 °通风竖井缩小了75%左右(模型实验中90 °模型通风竖井截面面积A=0.043 75 m2,15 °通风竖井截面面积A=0.011 32 m2),通风竖井长度亦有较大变化,90 °模型通风竖井长度L=17.5 cm,15 °模型通风竖井长度L=67.6 cm,通风竖井断面的当量直径也由0.184 2 m变为0.105 m.实验中排风量比率与通风井角度关系如图13.
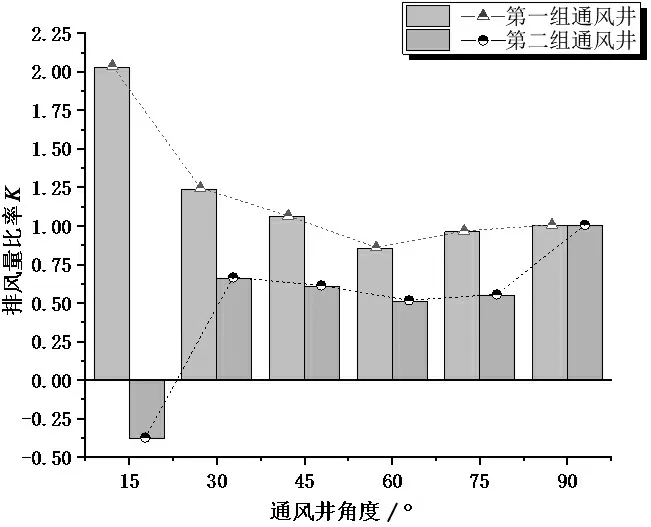
图13 两组通风竖井排风量比率K随通风竖井角度的变化趋势图
从图13中可以看出:
(1)第一组通风竖井的排风量始终大于第二组通风竖井,由此可见第一组排通风竖井的倾斜方向有利于隧道内部空气向外流出,而第二组通风竖井的倾斜方向相反,不利于空气流出;
(2)第一组通风竖井始终处于排风状态,且风量随着通风竖井倾斜度的增大,变化趋势为先减小后增大;第二组通风竖井的倾斜角度为90 °、75 °、60 °、45 °、30 °时,第二组通风竖井为排风状态,仅当倾斜角度为15 °时,第二组通风竖井为进风状态.
(3)第一、二组通风竖井的倾斜角度为15 °时,第一组通风竖井为排风状态,且排风量最大;第二组通风竖井则表现为进风状态.
将实验中测得的90 °通风竖井风量值乘上流量比尺=2 000,即可换算到实际隧道中的通风竖井进排风量,换算结果为:第一组通风竖井排风流量=70.2 m3/s,第二组通风竖井排风流量=41 m3/s.原型隧道根据理论计算,入口处的总进风量=481.041 m3/s,90 °的第一、二组通风竖井分别分担了入口处总进风量的14.6%和8.5%,即各自的分流率η.
隧道中污染物在无竖井的情况下全部随气流迁移扩散至隧道出口,而有竖井的情况下污染物能够沿途通过通风竖井排出,使得隧道出口处的污染物浓度低于无竖井下的浓度.而通风竖井角度的变化能在一定程度上改变通风竖井的分流率的大小(见表3),进一步改善隧道内以及出口处的空气质量.
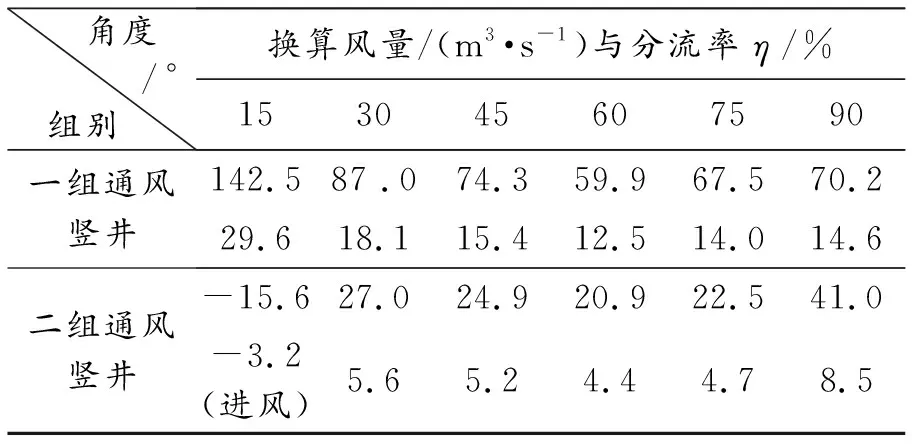
表3 换算风量值与分流率
4 通风井分流污染物的验算方法
将全长隧道分为3个计算区域i:隧道进口至第一组通风竖井之后为区域1,第一组通风竖井到第二组通风竖井为区域2,第二组通风竖井之前到隧道出口为区域3,如图13所示.
在各区域内,区域i汽车CO排放量Qcoi(mL/s)为
(11)
qcoi为汽车基准排量(m3/(km·辆)),Πfi为各种修正系数乘积,Nm为相应车型设计交通量(辆/h),N为车类别数,fm为车型系数.
不设置通风竖井时,隧道内从入口到出口没有空气交换,此时隧道末端浓度为:
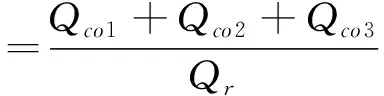
(12)
当设置15 °通风竖井时,第一组通风竖井为出风,出风量为Qe(mL/s),第二组通风竖井为进风,进风量为Qb(mL/s),那么
断面1浓度为:
(13)
断面2浓度为:
(14)
断面3浓度为:
(15)
隧道内其他断面处CO浓度亦可通过上述三个公式分段进行确定与验算,从而可得到全长隧道各处CO浓度分布.
5 结语
本文通过对隧道内的两组通风井在15 °、30 °、45 °、60 °、75 °和90 °五种角度情况下的分流规律进行了研究,模型实验结果与数值模拟得到的规律基本吻合.当通风井的角度减小时,第一组通风井均表现为排风状态,单位时间的排风量逐渐递增;而第二组通风井在90 °至30 °之前的排风量呈现递增趋势,15 °时变为进风状态,说明第二组通风井由排风转化为进风存在一个临界角度.
对于竖井型自然通风隧道而言,隧道内的污染物浓度稀释与排放、隧道内的压力脉动是影响自然通风效率的关键因素.本文研究确定了两组通风井角度在15 °时,能够实现预期的人为组织通风效果,即一组通风竖井主要负责排风,二组通风竖井主要负责进风.这种人为组织通风效果如同射流风机送排风的通风组合模式,第一组通风井将污染物随空气排出隧道,第二组通风井将隧道外空气吸入隧道以稀释污染物浓度;同时,两组通风井的风流一进一出可将隧道内的压力脉动进行有效降低,消除“哮喘效应”的影响,大大地提高自然通风的效率.
由于隧道出入口、通风井排风口空气流量的进出方向和大小不明确,会影响隧道中各区域污染物浓度的确定.本文通过通风井角度的优化,实现了隧道内外空气的有序交换,提出了通风井排风口、隧道出口的污染物浓度量化的验算方法,为通风设计、环境评价提供了依据.
需要指出的是,本文得出的结论主要基于西店湾隧道的几何参数,针对具体的工程宜开展具体的研究.

